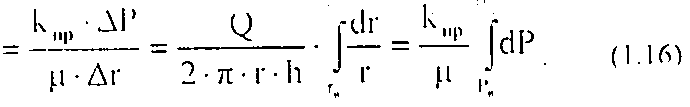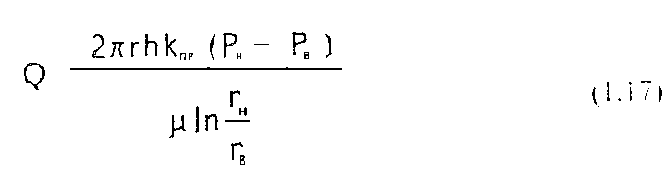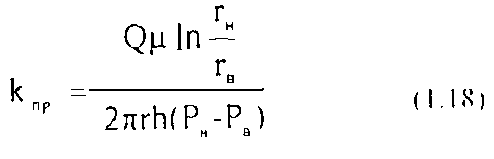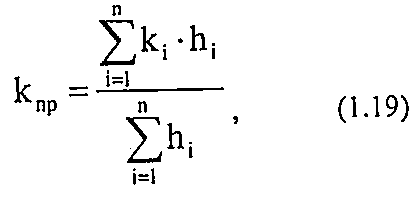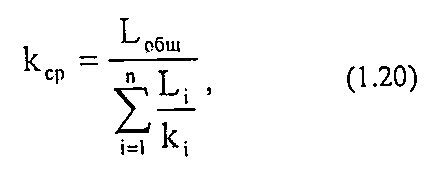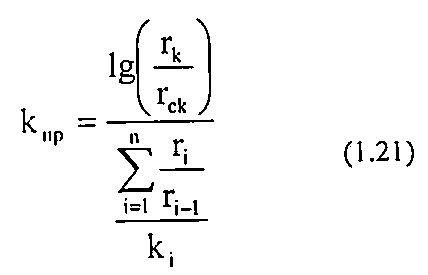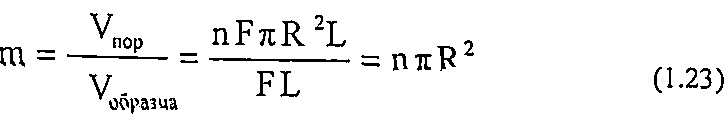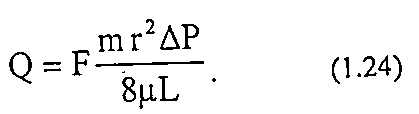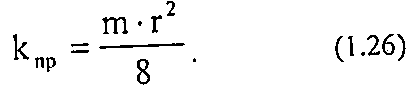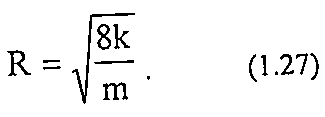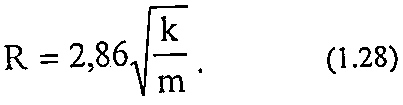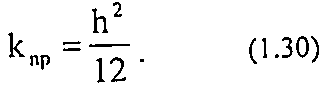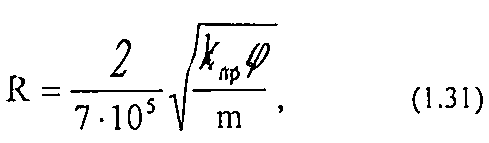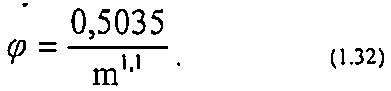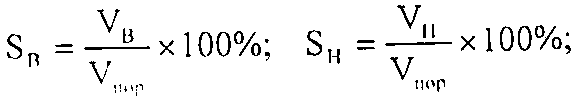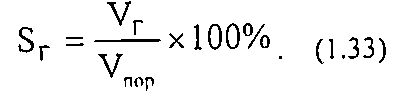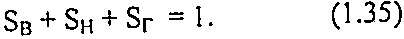Уравнение фильтрации нефти в пласте (8 видео)

РАСЧЕТ СКОРОСТИ ВЫТЕСНЕНИЯ НЕФТИ ИЗ ПЛАСТА ПОЛИМЕРНЫМ РАСТВОРОМ

При фильтрация водного раствора полимеров по мере увеличения градиента давления скорость его движения возрастает все медленнее по сравнению со скоростью воды по закону Дарси – проявляются дилатантные свойства полимеров.

Рисунок 5.1 – Зависимость скоростей фильтрации воды и дилатантной жидкости от градиента давления grad P

Скорость фильтрации жидкости нелинейно зависит от изменения градиента давления, с каждым приращением градиента давления она возрастает все меньше и меньше. Формулу закона полимерного раствора можно представить в виде:

, (5.1)

Где µ_ВП — вязкость водного раствора полимера.

С учетом фактора сопротивления R эту формулу записывают так:

, (5.2)

При фильтрации водного раствора полимера в пористой среде, перепад давления возрастает более динамично, чем это следует из закона Дарси. При этом, фильтрация водного раствора ПАА сопровождается его сорбцией с пористой средой. При незначительных концентрациях полимера в водном растворе можно с пользоваться изотермой Генри. В результате сорбции полимеров с пористой средой в процессе вытеснения нефти образуется фронт сорбции. Впереди фронта сорбции полимера в пласте движется вода, практически не содержащая полимеров.

Задача 5.1

Рассмотрим эффективность применения полимерного вытеснения нефти из пласта:

Из пласта длиной l = 200 м, шириной b = 400 м и толщиной, охваченной процессом вытеснения, h =20 м вытесняется нефть водным раствором полиакриламида. Вязкость нефти в пластовых условиях µ_н=7∙10 -3 Па∙с, вязкость воды µ_в= 10 -3 Па∙с , пористость пласта m = 0,2; s_св=0,05. Параметр изотермы сорбции Генри а=0,25 м 3 /м 3 .

Принимаем, что относительные проницаемости для нефти и воды как при вытеснении нефти водным раствором полимеров, так и чистой водой линейно зависят от водонасыщенности (рисунок 2.9), причем, согласно лабораторным экспериментальным данным S_* = 0,65; S_** = 0,7.

Расход закачиваемой в пласт воды q =800 м 3 /сут. Определим время t _∙ подхода к концу пласта (x = l) нефтяного вала х_∙, считая, что вытеснение нефти водой и водным раствором полимеров происходит поршневым образом.

Положим S₁=S_**=0,7; S₃=S_*=0,65. Следовательно конечная нефтеотдача при применении водного раствора полимеров возрастает на 5% по сравнению с нефтеотдачей при обычном заводнении.

Определим скорость фильтрации воды:

, (5.3)

Отношение скорости фронта сорбции w_сор к скорости фильтрации v равно:

, (5.4)

Отсюда w_сор= 0,1447∙10 -5 ∙0,242 = 0,35∙10 -6 м/с.

= ≈ 50,51, (5.5)

Относительная проницаемость: 1 – для нефти при вытеснении ее водой; 2 – для нефти при вытеснении ее водным раствором полиакриламида; 3 – для воды; 4 – для водного раствора ПАВ

Рисунок 5.2. — Зависимость относительных проницаемостей (k ) для нефти и воды, а также для и нефти и водного раствора полиакриламида от водонасыщенности (S)

После подстановки цифровых значений величин, входящих в правую часть уравнения , получим:

, (5.6)

, (5.7)

Отсюда S₂ = 0,627. Следовательно скорость движения в области смешивания нефти и полимерного раствора:

, (5.8)

Для того чтобы фронт вытеснения нефти преодолел длину пласта потребуется: (5.9)

За это время в пласт будет закачано 1,667∙10 6 м 3 (800 м 3 /сут.∙5,71года∙365 дней в году) водного раствора полиакриламида. При концентрации полимера в воде 0,5 кг на 1 м 3 в пласт будет введено 835 тонн полиакиламида.

ВАРИАНТЫ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ К ЗАДАЧЕ 5.1

Вариант	1	2	3	4	5
длина пласта l (м)	420	300	350	400	600
ширина пласта b (м)	240	180	200	300	550
нефтенасыщенная толщина h (м)	17	25	29	37	31
Пористость m	0,20	0,25	0,21	0,18	0,25
вязкость нефти в пластовых условиях μ_Н (Па∙с)	8∙10 -3	14∙10 -3	23∙10 -3	30∙10 -3	32∙10 -3
Расход закачиваемого в пласт водного раствора ПАА q (м 3 /сут)	450	600	700	850	820
насыщенность связанной водой s_CB	0,07	0,06	0,05	0,08	0,077
Параметр изотермы сорбции Генри а (м 3 /м 3 )	0,25	0,24	0,22	0,27	0,20

Определить основные параметры вытеснения нефти из пласта водным раствором ПАА: (скорость фильтрации, отношение скорости фронта сорбции к скорости фильтрации, скорость движения в области смешивания нефти и полимерного раствора, время прохождения водного раствора ПАА по длине пласта, объем закачивания водного раствора ПАА в нефтяной пласт)

Последнее изменение этой страницы: 2019-04-19; Просмотров: 597; Нарушение авторского права страницы

Содержание

Радиальная фильтрация нефти и газа в пористой среде
Добыча нефти и газа
Изучаем тонкости нефтегазового дела ВМЕСТЕ!
Проницаемость
🎥 Видео

Видео:Раздел 4 Основные модели фильтрацииСкачать

Радиальная фильтрация нефти и газа в пористой среде

Процесс притока пластовых флюидов из пласта в скважину описывается моделью радиальной фильтрации. В этом случае образец породы представляется в виде цилиндрического кольца с проводящими каналами в осевом направлении (рис. 1.7).

скважина

Рис. 1.7. Схема радиального притока жидкости в скважину

Площадь боковой поверхности цилиндра: F=2πrh, таким образом уравнение Дарси для радиальной фильтрации будет иметь следующий вид:

Отсюда дебит при радиальной фильтрации жидкости:

Таким образом, коэффициент проницаемости при радиальной фильтрации:

1.2.3. Оценка проницаемости пласта, состоящего из нескольких пропластков различной проницаемости

Пласт состоит, как правило, из отдельных пропластков, поэтому общая проницаемость пласта (к_пр) оценивается с учетом проницаемости пропластков и направления фильтрации.

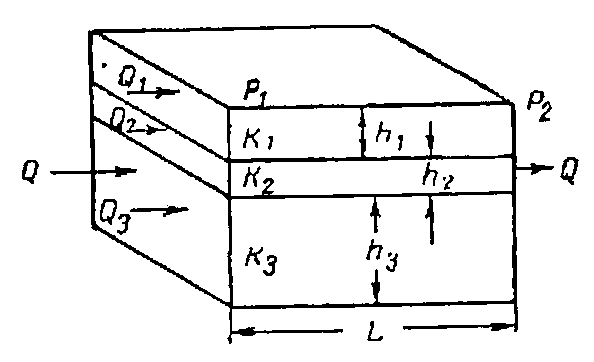
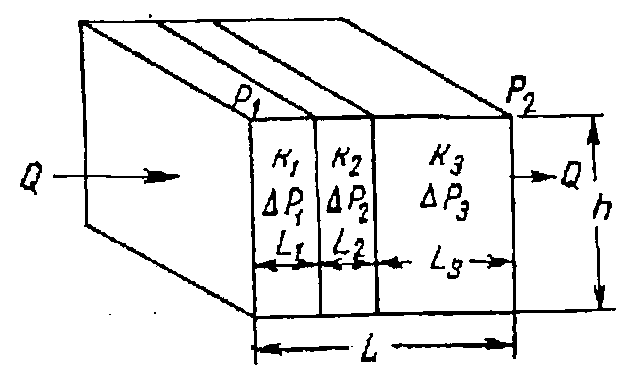
Рис.1.8 Линейная фильтрация в пласте, состоящем из нескольких изолированных пропластков различной мощности и проницаемости.

При линейной фильтрации жидкости в пласте, состоящем из нескольких однофазных пропластков различной мощности и проницаемости (рис. 1.8), общая проницаемость пласта рассчитывается следующим образом:

Где: h_i—мощность i-го пропластка

k_i — проницаемость i-ro пропластка.

Рис 1.9. Линейная фильтрация через пласт, имеющий несколько последовательно расположенных зон различной проницаемости

При линейной фильтрации жидкости через пласт, имеющий несколько последовательно расположенных зон различной проницаемости (рис. 1.9), коэффициент проницаемости пласта рассчитывается следующим образом:

где L_i — длина i-гo пропластка;

k_i — проницаемость i-гo пропластка.

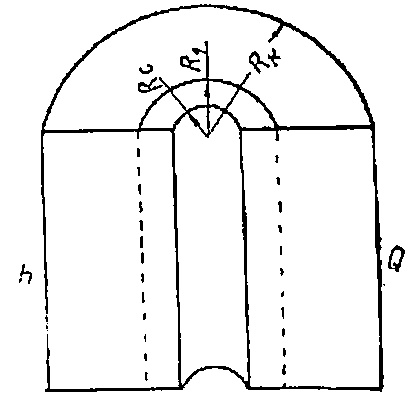
Рис. 1.10. Радиальная фильтрация через пласт, имеющий несколько концентрически расположенных зон различной проницаемости.

При радиальной фильтрации жидкости через пласт, имеющий несколько концентрически расположенных зон различной проницаемости (рис. 1.10), средняя проницаемость пласта оценивается следующим образом:

где г_к — радиус контура;

г_с — радиус скважины;

г_i — радиус i-гo пропластка;

k_j — проницаемость i-гo пропластка.

1.3.4. Классификация проницаемых пород

По характеру проницаемости (классификация Теодоровича Г.И.) различают коллектора:

По величине проницаемости (мкм 2 ) для нефти выделяют 5 классов коллекторов:

1. очень хорошо проницаемые (>1);

2. хорошо проницаемые (0,1 — 1);

3. средне проницаемые (0,01 — 0,1);

4. слабопроницаемые (0,001 -0,01);

L-длина порового канала;

n — число пор, приходящихся на единицу площади фильтрации;

F — площадь фильтрации;

µ- вязкость жидкости;

∆Р — перепад давлений,

Коэффициент пористости среды, через которую проходит фильтрация:

Следовательно, уравнение (1.22) можно переписать следующим образом:

Из уравнения Дарси следует, что:

Приравняв правые части уравнений (1.24) и (1.25) получим взаимосвязь пористости и проницаемости:

Из чего следует, что размер порового канала будет равен:

Если выразить проницаемость в мкм 2 , то радиус поровых каналов (в мкм) будет равен:

Оценка проницаемости для фильтрации через трещиноватые поры оценивается из соотношения уравнений Букингема и Дарси.

Потери давления при течении жидкости через щель очень малой высоты оцениваются уравнением Букингема:

где h — высота трещины;

v — линейная скорость фильтрации.

Подставив это выражение в уравнение Дарси, получим:

Соотношения (1.25) и (1.26) справедливы только для идеальной пористой среды (например, кварцевый песок).

Для реальных условий используется эмпирическое уравнение Котяхова:

где R- радиус пop;

φ — структурный коэффициент, описывающий извилистость порового пространства.

Значение φ можно оценить путём измерения электросопротивления пород. Для керамических пористых сред при изменении пористости от 0,39 до 0,28, по экспериментальным данным, φ изменяется от 1,7 до 2,6. Структурный коэффициент для зернистых пород можно приблизительно оценить по эмпирической формуле:

Виды проницаемости

Проницаемость абсолютная (физическая) — проницаемость пористой среды для газа или однородной жидкости при следующих условиях:

1. Отсутствие физико-химического взаимодействия между пористой

средой и этим газом или жидкостью.

2. Полное заполнение всех пор среды этим газом или жидкостью.
Для продуктивных нефтяных пластов эти условия не выполняются.

Проницаемость фазовая (эффективная) — проницаемость пористой среды для данного газа или жидкости при одновременном наличии в порах другой фазы или системы (газ-нефть, газ-нефть-вода).

При фильтрации смесей коэффициент фазовой проницаемости намного меньше абсолютной проницаемости и неодинаков для пласта в целом.

Относительная проницаемость — отношение фазовой проницаемости к

Проницаемость горной породы зависит от степени насыщения породы флюидами, соотношения фаз, физико-химических свойств породы и флюидов.

Фазовая и относительная проницаемости для различных фаз зависят от нефте-, газо- и водонасыщенности порового пространства породы, градиента давления, физико-химических свойств жидкостей и пористых фаз.

Насыщенность— ещё один важный параметр продуктивных пластов, тесно связанный с фазовой проницаемостью.

Предполагается, что продуктивные пласты сначала были насыщены водой. Водой были заполнены капилляры, трещины, каналы.

При миграции углеводороды, вследствие меньшей плотности, стремятся верхней части пласта, выдавливая вниз воду. Вода легче всего уходит из трещин и каналов, из капилляров вода не уходит в силу капиллярных явлений. Таким образом, в пласте остаётся связанная вода.

Чтобы определить количество углеводородов, содержащихся в продуктивном пласте необходимо определить насыщенность порового пространства породы нефтью, водой и газом.

Водонасыщенность S_В — отношение объёма открытых пор, заполненных водой к общему объёму пор горной породы. Аналогично определение нефте- и газонасыщенности:

Обычно для нефтяных месторождений S_В = 6-35%; S_Н = 65-94%. в зависимости от созревания пласта.

Для нефтяных месторождений справедливо следующее соотношение:

Для газонефтяных месторождений:

Пласт считается созревшим для разработки, если остаточная водонасыщенность S_В 3 , м 2 /сa_L-10 5 , 1/КГлина0,7550,990,97—Глинистые сланцы0,772154-2180,970,9Доломит0,931,1-4,980,86—Известняк1,12,180,910,5-0,89Кварц0,6922,491,361,36Песок0,80,3470,20,5Пластовые флюидыс, кДж/(кг-К)λ, Вт/(м-К)а-10 3 , м 2 /сa_L-10 5 , 1/КНефть2,10,1390,069-0,086—Газ4,150,5820,14—

Дата добавления: 2016-03-22 ; просмотров: 2965 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Лекция №2 Дифференциальные уравнения фильтрации флюидов в нефтегазонасыщенном пластеСкачать

Добыча нефти и газа

Видео:Лекция_Проницаемость_Закон_Дарси_09_10_2018Скачать

Изучаем тонкости нефтегазового дела ВМЕСТЕ!

Видео:РЕЖИМЫ НЕФТЯНЫХ ПЛАСТОВ. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ НЕФТЕГАЗОДОБЫЧИ.Скачать

Проницаемость

Проницаемость – это фильтрующий параметр горной породы, характеризующий её способность пропускать через себя жидкости и газы при перепаде давления.

Абсолютно непроницаемых тел в природе нет. При сверхвысоких давлениях все горные породы проницаемы. Однако при сравнительно небольших перепадах давления в нефтяных пластах многие породы в результате незначительных размеров пор оказываются практически непроницаемыми для жидкостей и газов (глины, сланцы и т.д.).

Хорошо проницаемыми породами являются: песок, песчаники, доломиты, доломитизированные известняки, алевролиты, а так же глины, имеющие массивную пакетную упаковку (рис. 1.4).

Рис. 1.4. Пример массивной пакетной упаковки глин – фильтрация происходит через каналы между пакетами

Рис. 1.5. Пример упорядоченной пакетной упаковки глин – фильтрация практически не происходит

К плохо проницаемым относятся: глины, с упорядоченной пакетной упаковкой, глинистые сланцы, мергели, песчаники, с обильной глинистой цементацией (рис. 1.5).

1.3.1. Линейная фильтрация нефти и газа в пористой среде

Для оценки проницаемости горных пород обычно пользуются линейным законом фильтрации Дарси. Дарси в 1856 году, изучая течение воды через песчаный фильтр (рис. 1.6), установил зависимость скорости фильтрации жидкости от градиента давления..

Рис. 1.6. Схема экспериментальной установки Дарси для изучения течения воды через песок

Согласно уравнению Дарси, скорость фильтрации воды в пористой среде пропорциональна градиенту давления:

, (1.7)

где Q – объёмная скорость воды;

v – линейная скорость воды;

F – площадь сечения, F = pd2/4;

L – длина фильтра;

k – коэффициент пропорциональности .

Нефть – неидеальная система (компоненты нефти взаимодействуют между собой), поэтому линейный закон фильтрации для нефти, содержит вязкость, учитывающую взаимодействие компонентов внутри нефтяной системы:

, (1.8)

где m – вязкость нефти.

В этом уравнении способность породы пропускать жидкости и газы характеризуется коэффициентом пропорциональности k (1.7), который называется коэффициентом проницаемости (kпр).

Размерность коэффициента проницаемости (система СИ) вытекает из соотношения:

, (1.9)

Размерность параметров уравнения Дарси в разных системах единиц

Объемный дебит, Q

Площадь поперечного сечения фильтра, F

Длина фильтра, L

Перепад давления, ∆P

Вязкость жидкости, µ

В системе СИ коэффициент проницаемости измеряется в м2; в системе СГС [kпр] = см2; в системе НПГ (нефтепромысловой геологии) [kпр] = Д (Дарси).

1 Дарси = 1,02×10-8 см2 = 1,02 · 10-12 м2 » 1 мкм2.

Проницаемостью в 1 м2 называется проницаемость пористой среды при фильтрации через образец площадью 1 м2 длиной 1 м и при перепаде давления 1 Па, при которой расход жидкости вязкостью 1 Па×с составляет 1 м3.

Пористая среда имеет проницаемость 1 Дарси, если при однофазной фильтрации жидкости вязкостью 1 спз (спуаз) при ламинарном режиме фильтрации через сечение образца площадью 1 см2 и перепаде давления 1 атм., расход жидкости на 1 см длины породы составляет 1 см3/сек.

Физический смысл размерности проницаемости – это площадь сечения каналов пористой среды, через которые идет фильтрация.

Существует несколько типов каналов:

Приведённые выше уравнения справедливы при условии движения несжимаемой жидкости по линейному закону Дарси.

В случае фильтрации газа это условие не выполняется. При перепаде давления объём газа изменяется, и оценивается по закону Бойля-Мариотта:

При Т = const, P·V = const (1.10)

При линейной фильтрации газа оценивается средняя скорость фильтрации (Vср):

Vcр· Pср = Vо ·Pо = V1· P1 = V2 · P2, (1.11)

Pср = (P1 + P2) / 2, (1.12)

Vcр = Vо·Pо / Pср = 2·Vо·Pо / (P1 + P2). (1.13)

Тогда, средний объёмный расход газа будет равен:

. (1.14)

Отсюда уравнение коэффициента проницаемости для газа:

. (1.15)

1.3.2. Радиальная фильтрация нефти и газа в пористой среде

Рис. 1.7. Схема радиального притока жидкости в скважину

Площадь боковой поверхности цилиндра: F=2prh, таким образом уравнение Дарси для радиальной фильтрации будет иметь следующий вид:

. (1.16)

Отсюда, дебит при радиальной фильтрации жидкости:

. (1.17)

Таким образом, коэффициент проницаемости при радиальной фильтрации:

. (1.18)

1.3.3. Оценка проницаемости пласта, состоящего из нескольких пропластков различной проницаемости

Пласт состоит, как правило, из отдельных пропластков, поэтому общая проницаемость пласта (kпр) оценивается с учетом проницаемости пропластков и направления фильтрации.

Рис. 1.8. Линейная фильтрация в пласте, состоящем из нескольких изолированных пропластков различной мощности и проницаемости.

При линейной фильтрации жидкости в пласте, состоящем из нескольких изолированных пропластков различной мощности и проницаемости (рис. 1.8), средняя проницаемость пласта рассчитывается следующим образом:

, (1.19)

где hi – мощность i-го пропластка;

ki – проницаемость i-го пропластка.

Рис. 1.9. Линейная фильтрация через пласт, имеющий несколько последовательно расположенных зон различной проницаемости.

, (1.20)

где Li – длина i-го пропластка;

ki – проницаемость i-го пропластка.

При радиальной фильтрации жидкости через пласт, имеющий несколько концентрически расположенных зон различной проницаемости (рис. 1.10), средняя проницаемость пласта оценивается следующим образом:

(1.21)