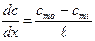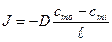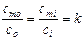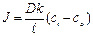Важной характеристикой мембран является их способность пропускать или не пропускать молекулы (атомы) и ионы. Вероятность такого проникновения зависит как от направления перемещения частиц (в клетку или из клетки), так и от разновидности молекул и ионов.
Эти вопросы относятся к явлениям переноса. Таким термином называют самопроизвольные необратимые процессы, в которых благодаря молекулярному движению из одной части системы в другую переносится какая-либо физическая величина.
Рассмотрим наиболее существенные для биологических мембран явления: перенос вещества (диффузию) и перенос заряда (электропроводность).
Как синоним переноса частиц в биофизике используется термин «транспорт частиц».
Основное уравнение диффузии имеет вид
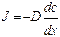
где J -плотность потока частиц, 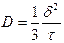
(1) называется уравнением Фика.
Уравнение Фика описывает диффузию в однородной среде. Модифицируем его для случая диффузии через мембрану. Обратим внимание на следующий известный факт: на границе раздела двух сред (например, воды и масла) обязательно имеет место скачкообразное изменение концентрации частиц диффундирующего вещества. Например, если в сосуд, в котором поверх воды налито масло, бросить соль, то ее концентрации в этих средах будут различны.
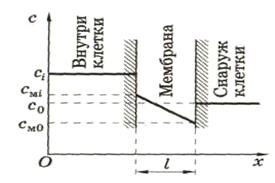
Пусть концентрация частиц, диффундирующих через мембрану, изменяется в мембране линейно (рис.11).
Рис.11. Распределение концентрации частиц, проходящих через мембрану
где 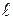
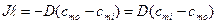
Практически легче определять концентрации частиц не внутри мембраны (cmi и cmo), а вне мембраны: в клетке (сi) и снаружи клетки (co). Предположим, что
где k -коэффициент распределения частиц между мембраной и окружающей средой. Тогда cmo = kco, cmi = kci , и имеем
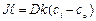
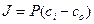
где 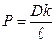
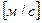
Перенос заряженных частиц. Электродиффузное уравнение Нернста-Планка
На мембране существует разность потенциалов, следовательно, в мембране имеется электрическое поле, которое влияет на диффузию заряженных частиц (ионов и электронов).
Плотность потока заряда дается выражением
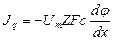
где φ – потенциал поля, F=eNA -постоянная Фарадея, Z – валентность, Um – подвижность диффундирующих частиц для одного моля.
В общем случае перенос ионов зависит от неравномерности их распределения и воздействия электрического поля. Суммарная плотность потока частиц определяется электродиффузным уравнением Нернста-Планка
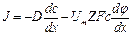
Для нейтральных частиц (Z=0) уравнение Нернста-Планка переходит в уравнение Фика.
- Биологические мембраны. Биоэлектрогенез (лекция 5)
- Описание презентации по отдельным слайдам:
- Дистанционное обучение как современный формат преподавания
- Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
- Инструменты онлайн-обучения на примере программ Zoom, Skype, Microsoft Teams, Bandicam
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- Поток вещества, растворяемогов биомимбране. Уравнение Фика, проницаемость
- 📺 Видео
Видео:Закон диффузии ФикаСкачать

Биологические мембраны. Биоэлектрогенез (лекция 5)
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Лекция 5
Биологические мембраны; Биоэлектрогенез
Ростов-на-Дону
2012
Содержание лекции №5
Биологические мембраны и их физические свойства.
Уравнения простой диффузии и электродиффузии. Уравнение Фика. Уравнение Нернста-Планка.
Виды пассивного транспорта.
Понятие об активном транспорте ионов через биологические мембраны.
Потенциал покоя и потенциал действия
и их физические свойства
В каждой клетке есть плазматическая мембрана, которая ограничивает содержимое клетки от наружной среды, и внутренние мембраны, которые формируют различные органоиды
клетки:
митохондрии,
Что есть мозг клетки?
Клетка- мельчайшая структурная единица живого организма
лизосомы
и т.п.
Она состоит из органических молекул, которая имеет толщину 6-10 нм и видима только посредством электронного микроскопа.
Биологическая мембрана (БМ) – это клеточная граница, которой свойственна полупроницаемость.
БМ –это глико – липо — протеидный комплекс
Как понимать полупроницаемость?
Что она дает?
Схема строения клетки , реконструированная по данным электронной микроскопии.
ВОПРОС:
Через биологическую мембрану происходит обмен:
вещество
энергия
клетка
окружающая среда
in
out
БМ – это кожа клетки
in
Клеточные сообщества существуют только благодаря передаче информации от клетки к клетке. Если информационные процессы угнетены
онкозаболевания организм нажимает кнопку на самоуничтожение.
информация
Общие
Механическая
Барьерная
Матричная
Специфические
Транспортная
Рецепторная
Генерация
БП
Принимает участие в
информационных
процессах в живой
клетке
Функции биологических мембран
Структура биологических мембран
БМ = липиды + белки
40%
Из липидной части наиболее важны для структуры фосфолипиды.
Основа фосфолипида – трехатомный
глицерин. К нему присоединяются жирные кислоты.
0,8 нм
1/4
3/4
Полярная часть, где фосфатная группа. «Любит воду». Гидрофильная часть.
Гидрофобная часть. «Хвосты» не любят взаимодействовать с водой.
Физико-химическое свойство фосфолипидов – амфофильность.
Насыщенная жирная кислота
Ненасыщенная жирная кислота
В воде молекулы фосфолипидов автоматически собираются в бислой (bilayer)
Бислой – это
каркас для БМ
Самосборка
Самовосстановление
Мембранные белки (большие глобулы).
На 1 молекулу белка приходится 80-90 молекул фосфилипидов.
Электростатические
взаимодействия
Периферические
Пример: ферменты, рецепторы
Схема расположения молекулы родопсина в биологической мембране (α – спираль, пронизывающая 7 раз фосфолипидный каркас)
Интегральные белки
Периферические белки
Какие белки легче удалить? А для каких нужен детергент?
Схематическое строение БМ
Поверхностные белки
толщина мембраны
Липидный бислой
Различные формы молекулярного движения в БМ
Вращение
Латеральная
диффузия
Перемещение молекул в пределах одной стороны бислоя.
ФЛИП-ФЛОП= перемещение молекул поперек БМ.
Один раз в 2 недели.
В 109 медленнее
Физические свойства БМ
Текучесть ≈ const
Жидкокристаллическая
структура
С = 1 мкФ/см2
БМ — конденсатор
Электросопротивление
105 Ом/см2
гораздо больше, чем у
технических изоляторов
Поверхностный заряд
Отрицательный.
Препятствует слипанию
клеток крови
εлипидов = 2,2
Плотность липидного
бислоя 800 кг/м3 .
Меньше, чем у H2O
Вязкость
η = 100 мПа٠с
(оливковое масло)
Модуль упругости
Е=109 Па
1. Жидкокристаллическая структура
Кристалл
твердый
жидкий
Жидкокристаллическая структура (ЖК)
транспорт
скелет
Фазовый переход при температуре 370 С
Обусловлена необычайно высокой подвижностью мембранных компонентов.
Жидкий кристалл Твердый кристалл
Мембрана сохраняется в ЖК состоянии благодаря температуре клетки и химическому составу жирных кислот.
2. Текучесть ≈ const
3. Вязкость
БМ как ЖК структура характеризуется определенной вязкостью.
η = 100 мПа٠с
(оливковое масло)
На вязкость клеточных мембран влияет содержание в них холестерина.
При повышении содержания холестерина
вязкость . Исчезают
транспортные свойства.
Как влияет?
Бляшки холестерина
в артериях
4. Поверхностный заряд на мембране.
Продуктивность клетки, т.е. ее энергия является измеряемой величиной. Здоровая клетка обладает напряжением 70-90 мВ.
В зависимости от здоровья, напряжение снижается до 20-30 мВ В связи с этим мы чувствуем усталость и изнуренность.
Вся патология на мембранном уровне!
Уменьшение вязкости БМ – причина разжижжения БМ при злокачественных опухолях – при лейкозе.
Вязкость меняется при многих заболеваниях, под действием ионизирующего Э/М излучения , ряда фармпрепаратов.
Вязкость БМ уменьшается при тиреотоксикозе,
а также под действием наркотических веществ, например, хлороформа.
Две стороны мембраны, наружная и внутренняя, различаются и по составу и по функциям.
Эта структурная асимметрия мембран приводит к векторной направленности процессов переноса.
Академик Владимиров Ю.А.
Пассивный транспорт – это перенос веществ через биологическую мембрану без затраты энергии.
Транспорт «под горку»- down hill
Диффузия молекул
Электродиффузия ионов
Уравнение
ФИКА
Уравнение НЕРНСТА -ПЛАНКА
ВИДЫ ПАССИВНОГО ТРАНСПОРТА
Диффузия –это самопроизвольный процесс проникновения массы вещества из области большей концентрации в область с меньшей концентрацией в результате теплового хаотичного движения молекул.
Параметры диффузии
ПЛОТНОСТЬ
ПОТОКА
ВЕЩЕСТВА:
in
out
Уравнения простой диффузии и электродиффузии
Плотность потока
вещества – это количество вещества в единицу времени через единицу площади.
Математическое описание процесса диффузии дал физиолог Фик в 1855 г.
Уравнение Фика является основой конструирования ряда биотехнических систем, например, в аппаратах:
«Искусственная
почка»
Экстракорпорального кровообращения
описывает пассивный транспорт неэлектролитов
C out
C in
C out
C in
in
out
Плотность потока вещества через биологическую мембрану прямо пропорциональна градиенту концентрации
in
D – коэффициент диффузии [м2/с]
Коэффициент диффузии D зависит от природы вещества и температуры и характеризует способность вещества к диффузии.
U=Um NA
U= v/F
D=UmRT
Где — подвижность диффундирующих молекул, выраженная для моля.
Um
Так как
grad C определить трудно, то для описания диффузии веществ через мембрану используют более простое уравнение.
NA
-число Авогадро
R- универсальная газовая постоянная
Т – термодинамическая температура
Уравнение диффузии для мембраны
Где Р- коэффициент проницаемости
in
out
C in
C out
Это более простое уравнение предложено Коллендером и Берлундом.
Плотность потока вещества через биологическую мембрану прямо пропорциональна разности концентраций внутри и снаружи клетки.
Коэффициент проницаемости
C out
C in
где l – толщина БМ
D- коэффициент диффузии
К- коэффициент распределения между липидной и водной фазами.
Р – зависит от температуры, природы вещества, от свойств БМ, ее функционального состояния.
Нет проницаемости мембраны вообще, а есть разная проницаемость БМ для тех или иных веществ.
Уравнения электродиффузии
Перенос ионов
зависит
от двух градиентов
градиента концентрации
grad C
электрического градиента
grad φ.
grad μ
μ
Уравнение Нернста – Планка
Уравнение Нернста – Планка описывает пассивный транспорт ионов
Z – валентность иона
F = 96500 Кл/моль – число Фарадея
C – молярная концентрация
Um – подвижность ионов для моля
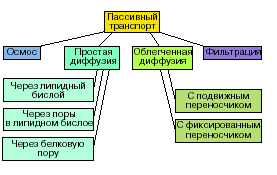
Разновидности пассивного транспорта
Простая физическая диффузия (O2, CO2, N2, яды, лекарства).
Через белок-канал (ионы).
Облегченная диффузия
(с носителем).
(АК,моносахариды, глюкоза)
Виды транспорта с носителем
Существуют системы переносчиков, которые
способны транспортировать более одного вещества
μ
out
Понятие об активном транспорте ионов через биологические мембраны
C2=С1
in
C1
Up hill- в горку
Активный транспорт – это перенос веществ (ионов) через БМ, связанный с затратой химической энергии (энергия метаболизма) из области МЕНЬШЕГО ! электрохимического потенциала в область большего электрохимического потенциала.
ВОПРОС: Что будет через некоторое время, если пассивный транспорт?
C1
C2
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 949 человек из 80 регионов
Курс повышения квалификации
Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
- Курс добавлен 23.11.2021
- Сейчас обучается 48 человек из 28 регионов
Курс повышения квалификации
Инструменты онлайн-обучения на примере программ Zoom, Skype, Microsoft Teams, Bandicam
- Курс добавлен 31.01.2022
- Сейчас обучается 33 человека из 19 регионов
Ищем педагогов в команду «Инфоурок»
Видео:Физиология дыхание. Газообмен в лёгких. Альвеолярно - капиллярное мембрана.Скачать

Дистанционные курсы для педагогов
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 565 554 материала в базе
Другие материалы
- 24.12.2020
- 132
- 0
- 03.12.2020
- 69
- 0
- 28.11.2020
- 64
- 0
- 22.11.2020
- 415
- 8
- 16.11.2020
- 136
- 0
- 19.08.2020
- 74
- 0
- 11.08.2020
- 302
- 2
- 10.07.2020
- 94
- 1
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 19.08.2020 796
- PPTX 4.7 мбайт
- 5 скачиваний
- Оцените материал:
Настоящий материал опубликован пользователем Макаренко Наталья Валерьевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 1 год и 1 месяц
- Подписчики: 0
- Всего просмотров: 22706
- Всего материалов: 225
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:МЕМБРАННЫЙ ТРАНСПОРТ: Активный и Пассивный, Диффузия, Ионные Каналы, Белки-транспортеры || СТУДЕНТАМСкачать

Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Тринадцатилетняя школьница из Индии разработала приложение против буллинга
Время чтения: 1 минута
Новые курсы: управление детским садом, коучинг, немецкий язык и другие
Время чтения: 18 минут
Профессия педагога на третьем месте по популярности среди абитуриентов
Время чтения: 1 минута
В Рособрнадзоре рассказали, как будет меняться ЕГЭ
Время чтения: 2 минуты
В Египте нашли древние школьные «тетрадки»
Время чтения: 1 минута
Объявлен конкурс дизайн-проектов для школьных пространств
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Видео:(АРХИВ) Явления переноса. Мембранный транспортСкачать

Поток вещества, растворяемогов биомимбране. Уравнение Фика, проницаемость
Проницаемость биологических мембран имеет большое значение для осморегуляции и поддержания постоянства состава клетки, её физико-химический гомеостаз; играет важную роль в генерации и проведении нервного импульса, в энергообеспечении клетки, сенсорных механизмах и др. процессах жизнедеятельности. Проницаемость биологических мембран обусловлена особенностями строения БМ, являющихся осмотическим барьером между клеткой и средой, и служит характерным примером единства и взаимосвязи между структурой и функцией на молекулярном уровне.
С точки зрения термодинамики движущим потенциалом любого выравнивающего процесса является рост энтропии. При постоянных давлении и температуре в роли такого потенциала выступает химический потенциал µ, обусловливающий поддержание потоков вещества. Поток частиц вещества пропорционален при этом градиенту потенциала
В большинстве практических случаев вместо химического потенциала применяется концентрация C. Прямая замена µ на C становится некорректной в случае больших концентраций, так как химический потенциал перестаёт быть связан с концентрацией по логарифмическому закону. Если не рассматривать такие случаи, то вышеприведённую формулу можно заменить на следующую:
которая показывает, что плотность потока вещества J [ 

Коэффициент диффузии D зависит от температуры. В ряде случаев в широком интервале температур эта зависимость представляет собой уравнение Аррениуса.
Дополнительное поле, наложенное параллельно градиенту химического потенциала, нарушает стационарное состояние. В этом случае диффузионные процессы описываются нелинейным уравнением Фоккера—Планка. Процессы диффузии имеют большое значение в природе:
· Питание, дыхание животных и растений;
· Проникновение кислорода из крови в ткани человека.
| 6.5 6.6 7.9 6.10 | 17:10:52 |
| 6.1 6.2 |
6.6 Диффузия электрическизаряженных частиц через мембрану.
Электрохимический градиент.
Электродиффузия — диффузия электрически заряженных частиц (ионов) под влиянием концентрационных и электрических градиентов. Ионы — атомы или группы атомов, которые приобретают электрический заряд, теряя или приобретая электроны. Липидный бислой мембраны непроницаем для ионов. Они могут проникнуть через плазматическую мембрану только посредством специальных структур — ионных каналов, которые образованы интегральными белками.
Движущей силой диффузии является не только разность концентрации ионов внутри и вне клетки, но также разность электрических потенциалов, создаваемых этими ионами по обе стороны мембраны. Следовательно, диффузионный поток ионов определяется градиентом электрохимического потенциала (электрохимический градиент).
Электрохимический потенциал является энергией ионов:
 |
μ0— стандартный химический потенциал, который зависит от химической природы вещества и температуры, R — универсальная газовая постоянная, T — температура, C — концентрация иона, z — электрический заряд, F — константа Фарадея, φ — электрический потенциал.
Зависимость потока ионов J от электрохимического градиента определяется уравнением Теорелла:
 |
где U — подвижность ионов, C — концентрация ионов, dμ/dx — электрохимический градиент.
Подставляя (6) в (7), можно получить уравнение Нернста-Планка с учётом двух градиентов, которые обуславливают диффузию ионов:
 |
Ионные каналы мембраны представляют собой интегральные белки мембраны, которые образуют отверстия в мембране, заполненные водой. В плазматической мембране обнаружен ряд ионных каналов, которые характеризуются высокой специфичностью, допускающей перемещение только одного вида ионов. Существуют натриевые, калиевые, кальциевые и хлорные каналы. Каждый из них имеет так называемый селективный фильтр, который способен пропускать только определённые ионы. Существует несколько теорий, объясняющих избирательность ионных каналов плазматической мембраны.
Проницаемость ионных каналов может изменяться благодаря наличию ворот, определенных групп атомов в составе белков, формирующих канал. Конформационные изменения ворот переводят канал из открытого состояния в закрытое и наоборот. Механизмы регуляции положения ворот могут отличаться в различных каналах. Некоторые из них открываются при изменениях электрического потенциала мембраны. Другие открываются под действием специфических химических веществ, выполняющих сигнальные функции.
Электрохимический градиент
Электрохимический градиент (DmX, уравнение 2–3). Пассивный транспортзаряженного растворённого вещества Х зависит как от разности концентраций вещества в клетке ([X]В) и вне (снаружи) клетки ([X]С), так и от разницы электрического потенциала вне (YС) и внутри клетки (YВ). Другими словами, DmX учитывает вклад как концентрационного градиента вещества (разность химического потенциала), так и вклад электрического потенциала по обе стороны мембраны (разность электрического потенциала).
| DmX | = | RT ln([X]В?[X]С) | + | zXF(YВ — YС) |
| разность электрохимической энергии (Дж/моль) | разность химической энергии (моль) | разность электрической энергии (мВ) |
где: zХ — валентность вещества X,
T — абсолютная температура,
R — газовая постоянная,
F — константа Фарадея.
Таким образом, движущей силой пассивного транспорта электролитовявляется электрохимический градиент — разность электрохимического потенциала (DmX) по обе стороны биологической мембраны.
6.7. (1)Поток вещества через мембрану при наличии осмотического и электрического градиентов. Уравнение Нернста – Планка.
На мембране существует разность потенциалов, следовательно в мембране имеется электрическое поле. Оно оказывает влияние на диффузию заряженных частиц (ионов и электронов). Между напряженностью поля и градиентом потенциала существует известное соотношение
В общем случае перенос ионов определяется двумя факторами: неравномерностью их распределения, т.е. градиентом концентрации и взаимодействием электрического поля
— уравнение Нернста – Планка.
F — число Фарадея, Z — валентность иона, T — абсолютная температура, R — газовая постоянная, 
Этоуравнениеописываетпроцесспассивноготранспортаионоввполеэлектрохимическогопотенциала и используется для установления зависимости плотности диффузного потока от концентрации ионов и от напряжения электрического поля.
Поток вещества через мембрану при наличии осматического и электрического градиентов. Уравнение Нериста-Планка
О́смос (от греч. ὄσμος — толчок, давление) — процесс односторонней диффузии через полупроницаемую мембрану молекул растворителя в сторону бо́льшей концентрации растворённого вещества (меньшей концентрации растворителя).
Осмос играет важную роль во многих биологических процессах. Мембрана, окружающая нормальную клетку крови, проницаема лишь для молекул воды, кислорода, некоторых из растворённых в крови питательных веществ и продуктов клеточной жизнедеятельности; для больших белковых молекул, находящихся в растворённом состоянии внутри клетки, она непроницаема. Поэтому белки, столь важные для биологических процессов, остаются внутри клетки.
Осмос участвует в переносе питательных веществ в стволах высоких деревьев, где капиллярный перенос не способен выполнить эту функцию.
Осмос широко используют в лабораторной технике: при определении молярных характеристик полимеров, концентрировании растворов, исследовании разнообразных биологических структур. Осмотические явления иногда используются в промышленности, например при получении некоторых полимерных материалов, очистке высоко-минерализованной воды методом обратного осмоса жидкостей.
Клетки растений используют осмос также для увеличения объёма вакуоли, чтобы она распирала стенки клетки (тургорное давление). Клетки растений делают это путём запасания сахарозы. Увеличивая или уменьшая концентрацию сахарозы в цитоплазме, клетки могут регулировать осмос. За счёт этого повышается упругость растения в целом. С изменениями тургорного давления связаны многие движения растений (например, движения усов гороха и других лазающих растений). Пресноводные простейшие также имеют вакуоль, но задача вакуолей простейших заключается лишь в откачивании лишней воды из цитоплазмы для поддержания постоянной концентрации растворённых в ней веществ.
Осмос также играет большую роль в экологии водоёмов. Если концентрация соли и других веществ в воде поднимется или упадёт, то обитатели этих вод погибнут из-за пагубного воздействия осмоса.
Нернста закон распределения
определяет относительное содержание в двух несмешивающихся или ограниченно смешивающихся жидкостях растворимого в них компонента; является одним из законов идеальных разбавленных растворов. Открыт в 1890 В. Нернстом.Согласно Н. з. р., при равновесии отношение концентраций третьего компонента в двух жидких фазах является постоянной величиной. Н. з. р. может быть записан в виде c1/c2=k, где c1 и c2 — равновесные молярные концентрации третьего компонента в первой и второй фазах; постоянная k — коэффициент распределения, зависящий от температуры. Н. з. р. позволяет определить более выгодные условия экстрагирования веществ из растворов
6.8.Пассивный транспорт вещества через мембраны. Виды пассивного транспорта.
Пассивный транспорт – это перенос вещества из мест с большим значением электрохимического потенциала к местам с его меньшим значением. Пассивный транспорт идет с уменьшением энергии Гиббса и поэтому этот процесс может идти самопроизвольно и без затраты энергии Пассивный транспорт не зависит от энергии, обеспечиваемой АТФ. В его основе лежит разность концентраций и зарядов и он всегда стремится выровнять концентрации частиц по разные стороны от мембраны, то есть свести к нулю их градиенты.
Виды пассивного транспорта:
1) Транспорт веществ через липидный бислой (простая диффузия)
2) Транспорт веществ через мембранные каналы
3) Транспорт веществ через специальные транспортные белки (облегченная диффузия)
Простая диффузия происходит без участия мембранного белка за счет тепловыхпрцессов- тепловой и физической дифузи, непосредственно через липидный бислой. Через него легко проходят газы, неполярные или малые незаряженные полярные молекулы.
Диффузию воды через мембраны называют осмосом. Вода, очень быстро проникает через липидныйбислой. Это объясняется тем, что ее молекула мала и электрически нейтральна.
Диффузия через мембранные каналы. Заряженные молекулы и ионы (Na+, K+, Ca2+, Cl-) не способны проходить через липидный бислой путем простой диффузии, тем не менее, они проникают через мембрану, благодаря наличию в ней особых белков, формирующих различные каналы.
Облегченная диффузия — транспорт веществ с помощью специальных транспортных белков, каждый из которых отвечает за транспорт определенных молекул
📺 Видео
Транспорт веществ через мембрану. Диффузия. Осмос и другие способы | ЕГЭ 2023Скачать

Клеточная мембрана: холестерин, белки-транспортеры, гликопротеины, гликолипидыСкачать

Строение клеточной мембраныСкачать

Лекция 24 Первый закон ФикаСкачать

Пассивный транспорт и избирательная проницаемость (видео 7) | Мембранный транспорт | БиологияСкачать

БФ - Явления переноса. Транспорт веществ через мембрануСкачать

Просто о сложном - ДиффузияСкачать

Мембранные потенциалы - Часть 1Скачать
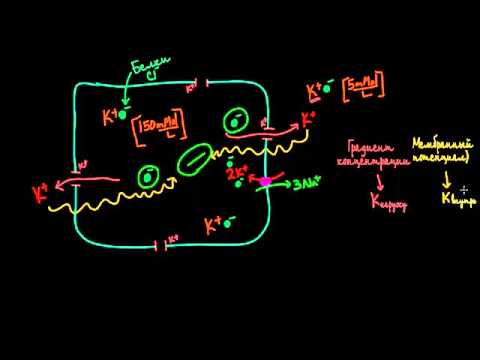
Физиология. Потенциал действияСкачать
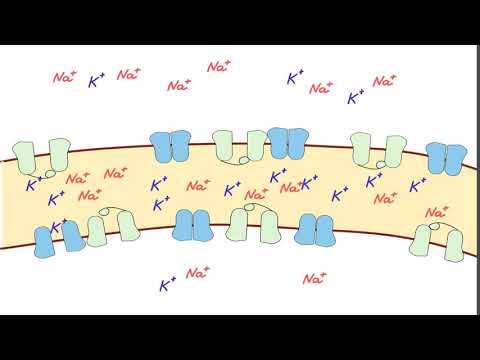
Жидкостно-мозаичная модель структуры клеточной мембраны (видео 1) | Мембранный транспорт | БиологияСкачать

Проницаемость и мембранные потенциалыСкачать

Транспорт веществ через мембрануСкачать

Биохимия. Лекция 28. Строение клеточной мембраныСкачать

10.1 Закон Фика и уравнение диффузии моноэнергетических нейтронов (часть 1)Скачать

Биологические мембраны и вторичные менеджеры | БиохимияСкачать

Потенциал покоя и равновесный потенциалСкачать