Исследование нелинейных систем автоматического управления связано с необходимостью составления и решения нелинейных дифференциальных уравнений. Поскольку единого общего решения для нелинейных дифференциальных уравнений разного вида не существует, то не представляется возможным создание обобщенного метода теории управления для исследования нелинейных систем, подобно случаю обыкновенных линейных систем.
Для исследования нелинейных систем в теории автоматического управления разработаны и используются частные методы, каждый из которых обладает определенными возможностями и эффективен в некоторой ограниченной области задач исследования. Наибольшее применение находят метод фазовых траекторий и амплитудно–частотный метод (метод гармонической линеаризации). Оба эти метода будут рассмотрены далее.
Метод фазовых траекторий заключается в том, что поведение исследуемой нелинейной системы рассматривается и описывается не во временной области (в виде уравнений процессов в системе), а в фазовом пространстве системы (в виде фазовых траекторий).
Состояние нелинейной системы автоматического управления характеризуется с использованием фазовых координат системы
задающих вектор состояния системы в фазовом пространстве системы
При введении в рассмотрение фазовых координат нелинейное дифференциальное уравнение порядка n для свободного процесса в нелинейной системе
преобразуется к системе из n дифференциальных уравнений первого порядка

Уравнение фазовой траектории может быть получено из приведенной выше системы уравнений первого порядка, связывающих фазовые координаты и учитывающих свойства системы, путем исключения времени. Фазовая траектория не отображает время процессов в системе.

Пример. Рассмотрим в качестве примера систему, свободный процесс в которой описывается дифференциальным уравнением второго порядка
где u(t) выходная величина системы.
Введем в рассмотрение фазовые координаты x=u(t) и y=du/dt. Теперь систему можно описать с учетом фазовых координат
Чтобы получить уравнение фазовой траектории из приведенной системы уравнений необходимо исключить время. В рассматриваемом случае это можно сделать, разделив первое уравнение на второе
В результате получено дифференциальное уравнение первого порядка, функция решения которого y(x)+C, где C – постоянная интегрирования, описывает фазовую траекторию. Порядок полученного дифференциального уравнения ниже порядка исходного уравнения для процесса в системе, следовательно, решить это уравнение проще.

При использовании метода фазовых траекторий для исследования нелинейных систем необходимо строить и исследовать фазовые траектории. Практическое графическое построение фазовой траектории возможно только на фазовой плоскости, т.е. в случае описания исследуемой системы только двумя фазовыми координатами.
Указанное обстоятельство ограничивает возможность применения метода фазовых траекторий системами второго порядка. В случае описания исследуемой системы дифференциальным уравнением выше второго порядка, это уравнение приходится упрощать и сводить к уравнению второго порядка, что неизбежно ведет к возрастанию погрешности исследования.
Видео:Теория автоматического управления. Лекция 1. Метод фазовой плоскостиСкачать

Виды фазовых портретов для линейных систем второго порядка
| Корни характеристического уравнения | Переходный процесс | Фазовая траектория |
1. a1=0, a2>0 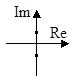 | 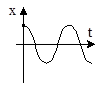 | 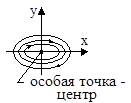 |
2. a1 2 >4a2, a1>0, a2>0 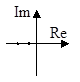 | 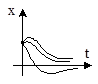 | 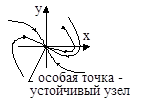 |
3. a2 2 0 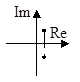 | 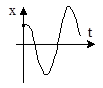 | 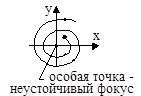 |
5. a1 2 0, a2>0 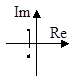 |  | 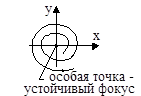 |
6. a1 2 >4a2, a1 0 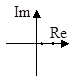 | 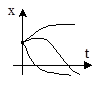 | 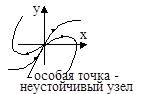 |
Вид и расположение фазовых траекторий, а также направление движения по ним изображающей точки дают возможность судить о характере движения системы и его устойчивости при различных начальных отклонениях. Особые точки и их характер определяют состояние равновесия исходной системы.
Реальные автоматические системы можно считать линейными в предположении малости отклонений переменных от их установившихся значений. За пределами указанной области картина фазовых траекторий может стать качественно иной. В частности, если по линейной теории система неустойчивая и процесс расходится, то может оказаться, что из-за фактической нелинейности характеристик он не будет расходящимся неограниченно. Картина фазовых траекторий для такой системы изображена на рис. 2.15,а. Здесь вблизи начала координат получаются спирали, как в неустойчивой линейной системе, но далее они приближаются асимптотически к замкнутому контуру ограниченных размеров. К нему же приближаются и все спирали, находящиеся вне контура. Такого рода замкнутый контур представляет собой особый вид линий на фазовой плоскости и называется устойчивым предельным циклом. Устойчивый предельный цикл соответствует автоколебаниям системы. Размеры предельного цикла представляют амплитуды колебаний самой величины x и скорости ее изменения y. Для определения периода автоколебаний необходимо решить уравнение системы во времени.
Рис. 2.15. Фазовые траектории нелинейных систем:
а — устойчивый предельный цикл; б — неустойчивый предельный цикл;
в — фазовый портрет системы с сепаратрисами
Замкнутые фазовые траектории на фазовой плоскости называются предельными циклами, которые могут быть как устойчивыми (рис. 2.15,а), так и неустойчивыми (рис. 2.15,б). К этим предельным циклам стремятся изображающие точки при различных начальных отклонениях по различным фазовым траекториям.
В различных частях фазовой плоскости фазовые траектории нелинейной системы могут быть различными (рис. 2.15,в). Линии, разделяющие фазовую плоскость на участки с различными фазовыми траекториями, называются сепаратрисами. Поведение системы в каждой области фазовой плоскости описывается своим дифференциальным уравнением.
Кроме того, для фазового портрета нелинейных систем с разрывными характеристиками характерно наличие линий переключения, которые также разделяют фазовую плоскость на ряд областей с различными фазовыми траекториями. При этом начальные значения переменных на каждом участке определяются через их конечные значения на предыдущем участке. Линии переключения характеризуются узловыми точками разрывных характеристик нелинейных элементов.
Замечание: координатами (x, y) фазовой плоскости могут служить не обязательно отклонение (ошибка) управляемой величины системы и ее скорость. Для этой цели могут быть взяты любые две переменные, однозначно характеризующие состояние системы второго порядка в произвольный момент времени.
Пример. Изобразим на фазовой плоскости переходный процесс и автоколебания в автоматической системе (рис. 2.1), линейная часть которой задана передаточной функцией
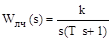
где k — коэффициент передачи;
T — постоянная времени,
а нелинейный элемент — статической характеристикой yн = F(x).
Р е ш е н и е. В качестве координат фазовой плоскости выбираем отклонение управляемой величины x и скорость ее изменения y = dx/dt. Запишем для ошибки x дифференциальное уравнение системы, описывающее ее свободное движение
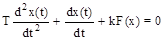
которое заменяем эквивалентными уравнениями первого порядка
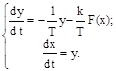
Разделив первое из уравнений (2.43) на второе, получаем дифференциальное уравнение фазовых траекторий
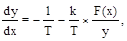
решение которого определяется характеристикой нелинейного элемента.
Рассмотрим фазовые портреты системы для некоторых типов нелинейных элементов.
1. Идеальное двухпозиционное реле (рис. 2.4,а) со статической характеристикой F(x) = csign(x).
Дифференциальное уравнение (2.44) фазовых траекторий в этом случае примет вид
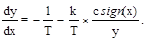
Переключение идеального реле происходит при x = 0. Следовательно, линия переключения на фазовой плоскости (рис. 2.16,а) совпадает с осью ординат.
Справа от линии переключения при x > 0 дифференциальное уравнение фазовых траекторий будет
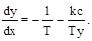
Его интегрирование дает уравнение фазовой траектории [2]
x = kcT ln½y + kc½ — Ty + c 0 , (2.47)
где c 0 — постоянная интегрирования, определяемая начальными условиями. Каждому конкретному c 0 соответствует определенная кривая на фазовой плоскости справа от линии переключения. Эти кривые имеют асимптоту y = -kc.
Слева от линии переключения при x 0 , (2.49)
согласно которому наносится семейство фазовых траекторий с асимптотой y = kc в левой фазовой полуплоскости.
На рис. 2.16,а изображены фазовые траектории системы для начальных условий (x0, 0).
Рис. 2.16. Фазовые траектории релейных систем:
а — с идеальным реле; б — с реле с гистерезисом
2. Двухпозиционное реле с гистерезисом (рис. 2.4,в) со статической характеристикой
Переключение реле с гистерезисом происходит при x = +b, если y > 0 (линия AB на рис. 2.16,б); если же y 0 к координатным осям, для которой xi = x0i, что соответствует отображению каждой точки полуоси 0X самой в себя, т.е. после обхода вокруг начала координат точка возвращается в исходное положение. Пересечение кривой xi = f(x0i) с прямой xi = x0i (точки A и B) определяют существование предельного цикла. Если указанная кривая и прямая не пересекаются, то автоколебания невозможны, а если касаются, то имеет место один предельный цикл.
Чтобы определить, какому типу предельного цикла это соответствует, надо взять на оси абсцисс начальную точку x0 сначала слева, а затем справа от точки пересечения и проследить ход точечного преобразования, как показано стрелками на рис. 2.19.
Рис. 2.19 соответствует двум предельным циклам, из которых меньший (точка A) неустойчив, а больший (точка B) устойчив. Следовательно, при начальных условиях (x0, y0), расположенных внутри меньшего предельного цикла, система устойчива, а при всяких других начальных условиях она стремится к установившемуся автоколебательному процессу.
ложение. Пересечение кривой xi = f(x0i) с прямой xi = x0i (точки A и B) определяют существование предельного цикла. Если указанная кривая и прямая не пересекаются, то автоколебания невозможны, а если касаются, то имеет место один предельный цикл.
Чтобы определить, какому типу предельного цикла это соответствует, надо взять на оси абсцисс начальную точку x0 сначала слева, а затем справа от точки пересечения и проследить ход точечного преобразования, как показано стрелками на рис. 2.19.
Рис. 2.19 соответствует двум предельным циклам, из которых меньший (точка A) неустойчив, а больший (точка B) устойчив. Следовательно, при начальных условиях (x0, y0), расположенных внутри меньшего предельного цикла, система устойчива, а при всяких других начальных условиях она стремится к установившемуся автоколебательному процессу.
Дата добавления: 2015-06-01 ; просмотров: 7377 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:ТАУ. Matlab/SIMULINK Фазовые портреты систем нелинейных диф. уравненийСкачать

Реферат: Методы исследования нелинейных систем
| Название: Методы исследования нелинейных систем Раздел: Рефераты по коммуникации и связи Тип: реферат Добавлен 12:55:57 30 августа 2009 Похожие работы Просмотров: 1435 Комментариев: 23 Оценило: 3 человек Средний балл: 5 Оценка: неизвестно Скачать | ||||||||||||||||||||||||||||||||||||||||||||||||||
 |
Рассмотрим свободное движение системы. Приэтом: U(t)=0, e(t)=– x(t)
В общем виде дифференциальное уравнение имеет вид


Это однородное дифференциальное уравнение 2-го порядка его характеристическое уравнение равно

Корни характеристического уравнения определяются из соотношений

Представим дифференциальное уравнение 2-го порядка в виде системы
уравнений 1-го порядка:

где 
В рассматриваемой линейной системе переменные x и y представляют собой фазовые координаты. Фазовый портрет строим в пространстве координат x и y, т.е. на фазовой плоскости.
Если исключим время из уравнения (1), то получим уравнение интегральных кривых или фазовых траекторий.

Это уравнение с разделяющимися переменными

Видео:Асташова И. В. - Дифференциальные уравнения. Часть 2 - Фазовый портретСкачать

Рассмотрим несколько случаев
1. Пусть корни характеристического уравнения (3) имеют вид


При этом переходной процесс описывается уравнениями
т.е. представляет собой незатухающие колебания с постоянной амплитудой А и начальной фазой – j.
На фазовой плоскости (рис. 4) эти уравнения представляют собой параметрические уравнения эллипса с полуосями А и wA (где A – постоянная интегрирования).
Уравнение эллипса можно получить решением уравнения фазовых траекторий

Состояние равновесия определяется из условия

Особая точка называется «центр» и соответствует устойчивому равновесию, так как фазовые траектории от нее не удаляются.
2. Пусть корни характеристического уравнения (3) имеют вид

При этом переходной процесс описывается уравнениями:
Из уравнения фазовых траекторий 
Это уравнение семейства гипербол при изменении A (рис 5).
 |
 |
Особая точка называется «седло». Уравнения асимптот (сепаратрис) при А = 0 имеют вид:
3. Пусть корни характеристического уравнения (3) имеют вид

Фазовая траектория имеет вид сворачивающейся спирали (рис. 6), а точка равновесия называется «устойчивый фокус».
4. Пусть корни характеристического уравнения (3) имеют вид

Переходный процесс представляет собой расходящиеся колебания, фазовая траектория – разворачивающаяся спираль. Особая точка называется «неустойчивый фокус» (рис. 7).
5. Пусть корни характеристического уравнения (3) имеют вид

Переходный процесс имеет апериодический характер. Особая точка называется «устойчивый узел» (рис. 8).
6. Пусть корни характеристического уравнения (3) имеют вид

Особая точка называется «неустойчивый узел» (рис. 9).
4. Методы построения фазовых портретов
Для построения фазовых портретов можно использовать различные методы: метод дифференциальных уравнений, метод изоклин, и др.
Метод дифференциальных уравнений . Сущность метода заключается в том, что по дифференциальным уравнениям отдельных участков нелинейного элемента строят соответствующие фазовые портреты на плоскости.
Метод изоклин – это метод линий постоянного наклона.
Пусть даны уравнения нелинейной системы:

где: 
Чтобы получить фазовый портрет исключим время:

Пусть 


Если провести достаточное число таких линий с соответствующими наклонами, то можно построить фазовый портрет системы. При этом точность зависит от числа изоклин. Направление движения определяется по правилу: если производная 
5. Построение фазового портрета нелинейной системы
Рассмотрим релейную следящую систему, схема которой приведена на рис. 11.
 |
 |
 |
 |


 | |
 | |
 |  |
 | |
 | |
 |  |

 |

 |
Если a¹b на вход НЭ с релейной характеристикой (рис. 12) подается сигнал 

Вследствие этого на двигатель подается напряжение ±
Для улучшения качества переходного процесса в систему может быть включена отрицательная обратная связь по скорости двигателя с помощью тахогенератора (ТГ).
Запишем уравнения элементов системы. Для двигателя постоянного тока с независимым возбуждением

Так как поток возбуждения 


Передаточную функцию для якорной цепи K1 (p) можно получить из ее дифференциального уравнения

Пусть
Для редуктора и угла поворота вала двигателя


На основании функциональной схемы и полученных передаточных функций элементов системы составляем структурную схему рис. 13
Для построения фазового портрета необходимо записать систему дифференциальных уравнений.
Рассмотрим свободное движение системы (b=0) при этом x = a.
Дифференциальное уравнение нелинейной системы имеет вид

Представим уравнение в виде системы уравнений:

Построим фазовый портрет. Для простоты построения фазового портрета делаем некоторые упрощения:
1) Пусть обратная связь по скорости – 
2) Характеристика нелинейного элемента однозначна (рис. 14).

С учетом принятых допущений система уравнений упрощается.

Построим характеристику для каждой зоны.
Пусть – a £ x £ a, ¦(x) = 0.
При этом исходная система имеет вид:

Решение этого уравнения имеет вид 
Определим равновесное состояние системы из условия:

Это условие выполняется при y = 0, т.е. точка вырождается в прямую линию y = 0 на интервале [– а, а]. Фазовые траектории на участке – а a, 

где ci — семейство изоклин, которое представляет собой прямые параллельные оси х, т.е. 



Задаваясь значениями 
Так как 

Пусть х 2 не применяется.
Рассмотрим несколько примеров построения фазовых портретов нелинейных систем управления
Пример 1. Пусть задана система, состоящая из линейной части и нелинейного элемента (усилитель с ограничением по модулю) (рис. 19). Это кусочно-линейная система, так как на отдельных участках она ведет себя как линейная (в области) – а, +а[). Допустим в области (] – а, +а[) коэффициент усиления большой и система неустойчива а фазовый портрет характеризуется особой точкой «неустойчивый фокус». За пределами области коэффициент усиления мал, допустим, что при этом система устойчива и характеризуется особой точкой – «устойчивый фокус».
При больших отклонениях x > |a| общий коэффициент усиления системы мал, система устойчива, процесс затухает.
При малых отклонениях общий коэффициент усиления системы большой – процесс расходится к замкнутой траектории, которая характеризует наличие устойчивых автоколебаний (рис. 20).
В этой системе три типа движений: автоколебания; сходящиеся колебания; расходящиеся колебания
Пример 2. Пусть задана система с характеристикой нелинейного звена типа «зона нечувствительности» (рис. 21). Необходимо построить фазовый
портрет данной системы, определить наличие предельных циклов и проанализировать их устойчивость.
 |
Пусть в области [-b, +b] система устойчива, при этом коэффициент усиления – К мал, переходный процесс затухает, особая точка «устойчивый фокус» вне области К – большой, переходный процесс расходится (рис. 22). Эта система имеет неустойчивый предельный цикл, т.е. автоколебания неустойчивы.
Для более сложных нелинейных элементов может быть несколько предельных циклов.
Видео:ТАУ. Matlab/SIMULINK Фазовые портреты нелинейных и линейных диф. уравненийСкачать

Пример Для заданной системы (рис. 23) построить примерный фазовый портрет.
Решение: Исходную схему можно представить в виде (рис. 24).
 |
Видео:4. Исследование фазовых траекторий.Скачать

Построим фазовый портрет
1) При – a +a f(x) = x – a, а система уравнений имеет вид
Для каждого сi определимугловой коэффициент наклона изоклины – к по формуле 
Таблица 1
| Сi | 0 | 1 | 2 | 3 | -1/2 | -2 | -3 | ¥ |
| k | -1 | -1/2 | -1/3 | -1/4 | -2 | 1 | 1/2 | 0 |
Таблица 2
| Ci | 0 | ±1 | ±1 | ±1 | ±1 | ±¥ |
| a | 0 | ±45 0 | ±63 0 | ±71 0 | ±80 0 | ±90 0 |
3) При x +1 f(x) = 1, а система уравнений имеет вид
Для каждого сi определимугловой коэффициент наклона изоклины – к по формуле 
🔍 Видео
Волков В. Т. - Дифференциальные уравнения - Фазовая плоскость. Фазовые траектории и их видыСкачать

Дифференциальные уравнения 6. Фазовые траектории. Особые точки автономных системСкачать

Лекция №5 Фазовые траектории автономных систем (разбор примеров)Скачать

Зарисовки по механике | потенциал и фазовые траекторииСкачать

4.2 Решение систем нелинейных уравнений. МетодыСкачать

Дополнительные главы ИДУ: Построение фазовых портретов | Занятие 3Скачать

Асташова И. В. - Дифференциальные уравнения. Часть 2 - Лекция 11Скачать

Способы решения систем нелинейных уравнений. Практическая часть. 9 класс.Скачать

Дифференциальные уравнения 20. Исследование поведения фазовых траекторийСкачать

Теория автоматического управления. Лекция 17. Задачи метода фазовой плоскостиСкачать

Нефёдов Н. Н. - Дифференциальные уравнения - Фазовая плоскость. Асимптотические методыСкачать

2) ТАУ для чайников. Часть 2.1: Математические модели...Скачать

Решение нелинейных системСкачать









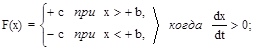
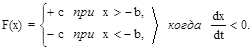



 – переменные, характеризующие поведение системы (одна из них может быть регулируемая величина);
– переменные, характеризующие поведение системы (одна из них может быть регулируемая величина);  – нелинейные функции; u – задающее воздействие.
– нелинейные функции; u – задающее воздействие. ,
, – начальные условия.
– начальные условия. не большие, то эту систему можно решать, как систему алгебраических уравнений. Решение можно представить графически.
не большие, то эту систему можно решать, как систему алгебраических уравнений. Решение можно представить графически. в функции времени. Значения
в функции времени. Значения 


























































