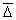Уравнение эйнштейна смолуховского для броуновского движения (3 видео)

Содержание

2.3.2. Броуновское движение
Уравнение Эйнштейна-Смолуховского для расчета величины среднего сдвига частиц при броуновском движении.
Уравнение эйнштейна смолуховского для броуновского движения
🎥 Видео

Видео:Модель броуновского движения.Скачать

2.3.2. Броуновское движение

В 1826 г. ботаник Р. Броун, наблюдая под микроскопом взвесь в виде растительной пыльцы (ликоподия), обнаружил, что частицы находятся в непрерывном движении, получившем название «броуновского». Он установил, что частицы не только перемещаются поступательно, но и поворачиваются вокруг своих осей, совершая вращательное движение. Броун проверил свои наблюдения на большом числе объектов и высказал ряд предположений относительно этого явления (так как в то время еще не существовало молекулярной теории строения вещества). Многие исследователи считали, что причиной броуновского движения являются внешние силы, а не внутренние – молекулярное движение жидкости.

Молекулярно-кинетические расчеты показывают, что коллоидные частицы способны проделывать элементарный путь l длиной 4·10 — 10 м за время 3·10 — 10 с.

В 1903 г. Р. Зигмонди и Зидентопф сконструировали ультрамикроскоп и с его помощью установили, что мелкие частицы находятся в еще более, чем крупные, интенсивном движении. Эти частицы не только колеблются около одного центра, но и совершают зигзагообразное движение. Движение крупных частиц более сложно, чем мелких, так как масса такой частицы намного превосходит массу молекул и, следовательно, каждое столкновение с движущимися молекулами отклоняет частицу на ничтожно малое расстояние.

Даже при наблюдении в ультрамикроскоп можно увидеть только суммарные пути за определенный промежуток времени. Наименьшее наблюдаемое человеком время 0,1 с, поэтому путь, составляющий длину пробега частицы, равен 10 7 l, т.е. 10 млн. элементарных движений, следовательно, возможность наблюдения элементарного пути исключается. Поэтому рассматривают средний сдвиг частицы

, (2.2.87)

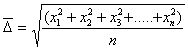
где x_i– элементарное смещение частицы по оси x.

В 1905-1908 гг. А. Эйнштейн и М. Смолуховский независимо друг от друга разработали теорию броуновского движения. В основе теории заложены следующие предпосылки:

– кинетическая энергия частицы, взвешенной в жидкости или газе, соответствует средней кинетической энергии молекул;

– экспериментатор может не считаться с фактически пройденным частицей путем или с фактической скоростью частицы, он может ограничиться средним смещением частицы за определенное время.

Вывод уравнения Эйнштейна — Смолуховского проводят следующим образом.

Рис. 2.14. Схема, поясняющая вывод уравнения Эйнштейна — Смолуховского

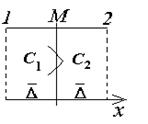
Представим мысленно плоскость М, проходящую через золь (рис. 2.14). Предположим, что концентрация С₁ в левой части больше концентрации С₂ в правой части. Коллоидные частицы в обеих частях системы совершают броуновское движение. Причина этого движения заключается в разности импульсов, полученных частицей с противоположных сторон. Естественно, чем меньше частица, тем менее вероятность компенсации импульсов и, следовательно, тем интенсивнее броуновское движение. 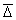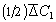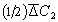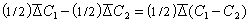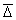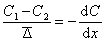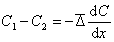Для частиц одинакового размера при определенной температуре среднее перемещение по направлению оси x влево или вправо за время t будет одинаковым. Следовательно, число частиц, которые пройдут расстояние от плоскости 1 до плоскости М, будет равно . Число частиц, проходящих от плоскости 2 до плоскости М, будет равно , в результате через плоскость за время t будет перенесено вещества. Если достаточно мало (или, что то же самое – мало время t), то

или (2.2.88)

(знак минус ставится по тем же причинам, что и в уравнении Фика).

Следовательно, очевидно, что количество вещества, перенесенного за 1 с, составит

. (2.2.89)

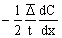
Если площадь плоскости М равна 1, то уравнение (2.2.89) перейдет в уравнение для диффузионного потока

. (2.2.90)

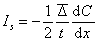
Сравнивая его с уравнением закона Фика, видим

. (2.2.91)

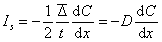
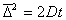
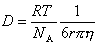
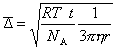
Поэтому , но

. (2.2.92)

. (2.2.93)

Из уравнения (2.2.93) видно, что 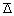пропорционален t 1/2 .

Справедливость этого уравнения подтвердил Сведберг, фотографируя коллоидные частицы через ультрамикроскоп. Он исследовал монодисперсный золь золота и получил очень хорошие результаты, рассчитывая число Авогадро по измеренным экспериментально 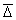для частиц с известным r.

Другой метод проверки уравнения основан на использовании частиц одного и того же вещества, но в разных дисперсионных средах с различной вязкостью. Тогда

, (2.2.94)

или . (2.2.95)

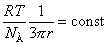
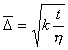
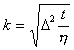
Сведберг изучал движение частиц платины в ацетоне, этилацетате, амилацетате, воде, нормальном пропиловом спирте, т.е. в жидкостях с различными значениями вязкости h. Таким образом, Сведберг экспериментально подтвердил справедливость уравнения Эйнштейна-Смолуховского, полученного теоретически.

Перрен воспользовался суспензией частиц гуммигута (сгущенного млечного сока каучуконосных деревьев) и провел ряд наблюдений броуновского движения частиц через микроскоп со специальным приспособлением. Через равные промежутки времени отмечалось положение частиц. На основании полученных данных проводилось вычисление числа Авогадро. Найденное значение составило N_А = 6,5×10 23 . Эти опыты стали окончательным доказательством молекулярно-кинетической теории строения материи.

Вместо того, чтобы измерять смещение отдельных частиц, можно определять число частиц в определенном малом объеме, который сообщается с большим объемом. Оказывается, что число частиц в таком микроскопическом объеме непрерывно меняется, хотя, согласно второму закону термодинамики, должно было быть равным и постоянным в любой момент времени.

Если рассматривать малый объем, то число частиц будет небольшим и его можно подсчитать. Если производить подсчет числа частиц через некоторое время, то окажется, что это число не постоянно. Такое изменение числа частиц в малом объеме носит название флуктуации. Теория этого явления была разработана Смолуховским и проверена им на результатах исследования золей Сведбергом. Теория флуктуации также определяет границы применимости второго начала термодинамики.

Видео:Относительность 19 - Уравнение ЭйнштейнаСкачать

Уравнение Эйнштейна-Смолуховского для расчета величины среднего сдвига частиц при броуновском движении.

Количественной характеристикой броуновского движения принято считать средний сдвиг Dх частицы за время t, т. е. наблюдаемую проекцию отрезка прямой, соединяющей начальную точку движения (при t = 0), с положением частицы в момент t, на горизонтальную плоскость (рис. 7.1).

Уравнение эйнштейна смолуховского для броуновского движения

Рис. 7.1. Средний сдвиг частицы при броуновском движении

Поскольку перемещение каждой частицы случайно, среднее арифметическое смещение всех частиц при достаточно большом их числе оказывается равным нулю (в отсутствие направленного потока жидкости или градиента концентрации дисперсной фазы). Однако частицы движутся, и каждая из них уходит от исходного положения. Поэтому при изучении диффузии производится усреднение таким образом, чтобы смещения в различных направлениях не вычитались, а складывались. А именно, усредняются квадраты проекций смещения. При этом получается предложенная А. Эйнштейном величина, называемая средним квадратичным сдвигом Dх 2 . В отличие от реального пути частицы, изменяющего направление до »10 20 раз в секунду, усреднённая величина Dх 2 может быть точно вычислена на основании законов статистики. Для сферической частицы с радиусом r она прямо пропорциональна абсолютной температуре Т и времени наблюдения t и обратно пропорциональна коэффициенту Стоксагидродинамического (вязкого) сопротивления среды B = 6phr:

где К – коэффициент пропорциональности, в соответствии с теорией Эйнштейна равный

(k – константа Больцмана). Отсюда получаем уравнение Эйнштейна – Смолуховскогодля величины среднего квадратичного сдвига

или для среднего сдвига

где D — коэффициент диффузии частиц данного вещества в данной среде.

94. Осмотическое давление коллоидных растворов.Осмотический метод определения размеров коллоидных частиц.

Т. Грэму при исследовании коллоидных растворов не удалось обнаружить у них осмотического давления. Этот факт он положил в основу деления растворов на коллоидные и истинные. Однако более поздние исследования показали, что и в коллоидных системах можно наблюдать измеримое, хотя и очень малое по величине осмотическое давление.

Для истинных растворов в соответствии с законом Вант-Гоффа осмотическое давление p может быть рассчитано по уравнению

где C — молярная концентрация растворённого вещества.

В дисперсных системах концентрацию дисперсной фазы принято выражать числом частиц (мицелл), содержащихся в единице объёма. Эта величина называется численной или частичной концентрацией и обозначается n. Выведем соотношение между молярной концентрацией вещества в растворе и числом частиц, из которых оно состоит. Молярная концентрация представляет собой отношение количества вещества в молях к объёму раствора:

Выражая количество молей через число молекул, содержащихся в нём, получим

а так как x/V = n (n — объёмная концентрация молекул), то

Если же под С подразумевается молярная концентрация коллоидных частиц, тогда n — объёмная концентрация этих частиц, или, иначе, частичная концентрация золя.

Поэтому уравнение для осмотического давления коллоидных растворов будет выглядеть так:

или ,

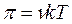
где k – константа Больцмана.

Из этого уравнения следует, что осмотическое давление увеличивается с ростом числа частиц в единице объёма даже при постоянной массе дисперсной фазы (с ростом дисперсности, например, при пептизации). Так как при одинаковой массовой концентрации n зависит от объёма частиц, то можно сказать, что осмотическое давление дисперсных (коллоидных) систем обратно пропорционально кубу радиуса их частиц.

Таким образом, закон Вант-Гоффа справедлив и для лиозолей. Однако простой расчёт показывает, что при одинаковой массовой концентрации частичные концентрации золей и тем более грубодисперсных систем обычно очень малы по сравнению с концентрацией молекул в истинных растворах. Поэтому в соответствии с выведенным уравнением и осмотическое давление в них должно быть намного меньше, а именно, во столько раз, во сколько раз частица дисперсной фазы больше, чем отдельная молекула или ион. Так, осмотическое давление коллоидных растворов в сотни и тысячи раз меньше, чем у истинных растворов. Столь малые значения очень трудно измерить с необходимой точностью, а в грубодисперсных суспензиях, пастах и эмульсиях осмотическое давление практически отсутствует.

Следует, однако, помнить, что речь идёт только об осмотическом давлении, обусловленном частицами дисперсной фазы. Надо учитывать, что в коллоидных растворах и в других дисперсных системах обычно присутствуют растворённые низкомолекулярные вещества – или в виде примесей, или в качестве стабилизаторов. Они тоже вносят свой вклад в общее осмотическое давление, поэтому его реальное значение несколько выше, чем рассчитанное исходя только из концентрации частиц дисперсной фазы.

Ещё одной особенностью осмотического давления золей является его непостоянство. Из-за идущих в той или иной степени процессов скрытой коагуляции частичная концентрация всё время уменьшается, что и вызывает снижение p во времени.

Низкое осмотическое давление является одной из причин лечебного, в частности, обеззараживающего или вяжущего действия коллоидных лекарственных средств – колларгола, протаргола и т. п. При соприкосновении их с клетками, в том числе с микробными, начинается интенсивный осмотический приток воды внутрь клеток, что приводит к гибели микробов вследствие лизиса.

Последнее изменение этой страницы: 2017-03-17; Просмотров: 2629; Нарушение авторского права страницы

Видео:Броуновское движениеСкачать

Уравнение эйнштейна смолуховского для броуновского движения

«Существенный признак того, что в обыденной жизни и в науке мы обозначаем как случайность,
можно кратко определить следующим образом: малые причины — большие следствия.»
М. Смолуховский

С 1913 года — профессопр экспериментальной физики Краковского университета (в 1917 году также его ректор).
Умер 5 сентября 1917 года в Кракове во время эпидемии дизентерии.

Польским физическим обществом учреждена медаль Смолуховского, вручаемая с 1965 года за достижения в области физики. Лауреаты медали имени Смолуховского

Броуновское движение — беспорядочное движение мельчайших частиц, взвешенных в жидкости или газе, происходящее под действием ударов молекул окружающей среды; открыто Р. Броуном в 1827 г.
Первая количественная теория броуновского движения была дана Альбертом Эйнштейном и М. Смолуховским в 1905-06 гг. на основе молекулярно-кинетической теории. Было показано, что случайные блуждания броуновских частиц связаны с их участием в тепловом движении наравне с молекулами той среды, в которой они взвешены. Частицы обладают в среднем такой же кинетической энергией, но из-за большей массы имеют меньшую скорость. Теория броуновского движения объясняет случайные движения частицы действием случайных сил со стороны молекул и сил трения. Согласно этой теории, молекулы жидкости или газа находятся в постоянном тепловом движении, причем импульсы различных молекул не одинаковы по величине и направлению.
Выводы теории броуновского движения были подтверждены измерениями Ж. Перрена и Т. Сведберга в 1906 г. На основе этих соотношений были экспериментально определены постоянная Больцмана и постоянная Авогадро.

Работы Эйнштейна и Смолуховского, вызванные необходимостью дать объяснение броуновскому движению, вышли далеко за пределы этой скромной цели. Эти ученые создали теорию флуктуации, радикально расширив статистическую термодинамику. В частности, современная теория фазовых переходов является флуктуационной, а построенная в начале XX века теория флуктуации служит для нее основой. Важно подчеркнуть, что больцмановские идеи о статистическом характере второго закона термодинамики были развиты и доведены до современного уровня именно Эйнштейном и Смолуховским. Они показали, что второй закон справедлив лишь с точностью до флуктуации, которые в малом пространственном и временном масштабе постоянно изменяют преимущественное направление кинетических процессов.

Смолуховскому принадлежит также объяснение невозможности «обхода» второго закона

термодинамики с помощью некоторого устройства молекулярных размеров, управляющего флуктуационными процессами. Такое устройство, или эквивалентное ему в смысле динамики маленькое разумное гипотетическое существо, появилось на свет в результате фантазии Максвелла и получило название «демон Максвелла», которое приводит к некоторому парадоксу. Его блестяще разрешил Смолуховский. Согласно его соображениям, суть дела заключается в том, что сортировочное устройство (или, если угодно, демон) с необходимостью должно быть молекулярных размеров или включать в себя соответствующий фрагмент. А такой объект будет подвержен нерегулярным тепловым флуктуациям и в силу этого будет неспособным к целенаправленному отбору необходимых молекул.

Другим выдающимся достижением Смолуховского было объяснение голубого цвета неба. Собственно говоря, такое объяснение вроде бы уже существовало. Крупнейший английский ученый лорд Рэлей еще в 1871 году показал, что интенсивность света, рассеянного на большом количестве посторонних объектов, малых по сравнению с длиной его волны, пропорциональна четвертой степени частоты света. Однако Рэлей ошибался относительного того, на каких именно маленьких частицах рассеивается свет в атмосфере Земли. Он считал, что ими являются сами молекулы, которые двигаются в разные стороны с различными скоростями. Такое отождествление оказалось неверным, что было доказано выдающимся русским ученым Л.Мандельштамом в 1907 году: несмотря на движение молекул, рассеянные волны, исходящие от разных элементарных объемов газа, компенсируют друг друга. Уже на следующий год Смолуховский нашел правильное решение, предположив неоднородность среды, присущую ей из-за непрекращающихся тепловых флуктуации. Тогда центрами рассеяния можно считать флуктуации плотности молекул газов, образующих атмосферу. Он подтвердил свою теорию собственноручно проведенным экспериментом — наблюдая голубой оттенок чистого (профильтрованного) воздуха в трубе, через которую были направлены лучи света от искусственного источника. Окончательную точку поставил Эйнштейн, получивший формулу для интенсивности рассеянного света на основании идеи Смолуховского. Интересно, что рассчитанная зависимость интенсивности от длины волны (частоты) и объема, на котором происходит рассеяние, совпадает с соответствующими зависимостями, найденными Рэлеем, т.е. несмотря на неверные исходные соображения британский ученый, руководствуясь своей фантастической интуицией, получил верную формулу!

Смолуховскому принадлежит также качественное объяснение явления критической опалесценции, т.е. резкого усиления рассеяния света на флуктуациях вблизи критической точки (например, в системе жидкость — газ). Он показал, что флуктуации кардинально усиливаются в этом случае, и, следовательно, рассеяние света на них резко возрастает. В окрестности данной точки, которой достигают на опыте соответствующим изменением давления и температуры, разница между жидкостью и газом исчезает. Если давление фиксировано, то интенсивность рассеянного излучения при этом возрастает обратно пропорционально малой разности между температурой наблюдения и критической температурой. Критическую опалесценцию легко наблюдать в школьной лаборатории. Она представляет собой еще одну наглядную демонстрацию существования флуктуации плотности.

В области коллоидной химии Смолуховский является одним из создателей теории электрофореза. Электроосмос и электрофорез были открыты Ф. Ф. Рейссом в 1809, который наблюдал вызванное внешним электрическим полем перемещение жидкости в U-образной трубке, перегороженной в нижней части мембраной из кварцевого песка, и движение глинистых частиц в покоящейся жидкости при наложении электрического поля. Г. Видеман установил (1852), что скорость электроосмотического течения пропорциональна силе тока и отношение не зависит от площади сечения и толщины мембраны.
В 1859 Г. Квинке предположил, что должно иметь место явление, обратное электроосмосу, и наблюдал возникновение потенциала течения на мембранах различной природы, а в 1880 Э. Дорн обнаружил возникновение разности потенциалов в трубке, заполненной водой, при центрифугировании в ней суспензии кварца.
Различные аспекты теории электрокинетических явлений были предложены Г. Гельмгольцем (1879) для простейшей модели ДЭС как молекулярного конденсатора, затем М. Смолуховским (1906) для случая протяженного ДЭС. Именно Смолуховский вывел формулу для расчета скорости электрофореза и дал количественную теорию седиментационного потенциала. Ему же удалось выяснить сущность отличия термодинамического -потенциала от электрокинетического -потенциала.

В 1916 году Смолуховским была разработана теория быстрой коагуляции.
При разработке своей теории он исходил из следующих предпосылок:

частицы дисперсной фазы сферические, а сами дисперсные системы являются монодисперсными, т.е. содержат частички одного размера;
скорость коагуляции определяется тремя факторами: – радиусом сферы сил притяжения частиц; – интенсивностью броуновского движения, которая определяет число столкновений в единицу времени и характеризуется коэффициентом диффузии D; – начальной концентрацией частиц n₀;
между частицами существуют только силы притяжения.

Смолуховский предложил рассматривать процесс коагуляции как попарное слипание частиц, чем формально уподобил процесс коагуляции химической реакции второго порядка. Считается, что вероятность одновременного столкновения трех частиц столь мала, что такие столкновения можно не учитывать.

В связи с приведенным выше обсуждением важнейших достижений Смолуховского необходимо отметить, что не только его конкретные предсказания и объяснения различных явлений сыграли важную роль в развитии физики XX столетия. Прежде всего сам глубокий, образный и убедительный стиль его работ, использующий математический аппарат теории вероятностей и проникнутый ее духом, изменил инструментарий и научный словарь последующих поколений физиков-теоретиков. Смолуховский внес решающий вклад в осознание научной общественностью объективного характера понятия вероятности. Как любил говорить выдающийся русский физик Л.Ландау, метод важнее результата, поскольку мощный метод позволяет получить множество новых ценных результатов.

Занятия любимой наукой, преподавательские и семейные обязанности не исчерпывали круг интересов Смолуховского. Кроме музыки и акварельной живописи, он увлекался и альпинизмом. Это пристрастие он воспринял от старшего брата — Тадеуша, химика, бывшего выдающимся альпинистом своего времени. Братья были широко известны как пара профессиональных альпинистов. Напрашивается аналогия с — не менее известными датскими футболистами Борами — братьями Нильсом (великий физик, создатель теории атома) и Харальдом (известный математик). В 1911 — 1912 годах Мариан Смолуховский был президентом туристской секции Польского общества Татр, а в 1916 году получил «Серебряный эдельвейс» от Немецко-австрийского альпийского общества.

Несмотря на глубокую близость к искусству и литературе своего времени, выдающийся физик, скорее всего, был бы весьма удивлен, узнав, что лично он стал одним из героев книги «Inferno» («Ад») шведского писателя-модерниста Ю.Стриндберга. История этого эпизода известна от самого автора романа. Он писал, что во время пребывания в Париже случайно обратил внимание на несколько писем, лежавших на конторке портье. Одно из них было отправлено из Вены и заинтересовало писателя адресатом с псевдонимом (так думал Стриндберг) «Шмуляховский». Славянская фамилия показалась Стриндбергу такой странной, что он предположил, что за ней скрывается переодетый дьявол. А в действительности это было письмо к молодому Смолуховскому, который находился в Париже в научной командировке в 1895 — 1896 годах.