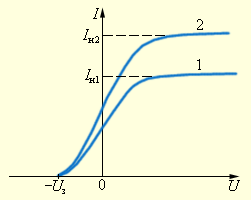Уравнение эйнштейна и его физический смысл (6 видео)

Уравнение эйнштейна и его физический смысл

Как можно было бы объяснить фотоэффект с точки зрения классической электродинамики и волновых представлений о свете?

Известно, что для вырывания электрона из вещества требуется сообщить ему некоторую энергию A , называемую работой выхода электрона. В случае свободного электрона в металле это работа по преодолению поля положительных ионов кристаллической решетки, удерживающего электрон на границе металла. В случае электрона, находящегося в атоме, работа выхода есть работа по разрыву связи электрона с ядром.

В переменном электрическом поле световой волны электрон начинает совершать колебания.

А если энергия колебаний превысит работу выхода, то электрон будет вырван из вещества.

Однако в рамках таких представлений невозможно понять второй и третий законы фотоэффекта. Почему кинетическая энергия выбитых электронов не зависит от интенсивности излучения? Ведь чем больше интенсивность, тем больше напряженность электрического поля в электромагнитной волне, тем больше сила, действующая на электрон, тем больше энергия его колебаний и с тем большей кинетической энергией электрон вылетит из катода. Но эксперимент показывает иное.

Откуда берется красная граница фотоэффекта? чем «провинились» низкие частоты? Казалось бы, с ростом интенсивности света растет и сила, действующая на электроны; поэтому даже при низкой частоте света электрон рано или поздно будет вырван из вещества когда интенсивность достигнет достаточно большого значения. Однако красная граница ставит жесткий запрет на вылет электронов при низких частотах падающего излучения.

Кроме того, при освещении катода излучением сколь угодно слабой интенсивности (с частотой выше красной границы) фотоэффект начинается мгновенно в момент включения освещения. Между тем, электронам требуется некоторое время для «расшатывания» связей, удерживающих их в веществе, и это время «раскачки» должно быть тем больше, чем слабее падающий свет. Аналогия такая: чем слабее вы толкаете качели, тем дольше придется их раскачивать до заданной амплитуды. Выглядит опять-таки логично, но опыт единственный критерий истины в физике! этим доводам противоречит.

Так на рубеже XIX и XX столетий в физике возникла тупиковая ситуация: электродинамика, предсказавшая существование электромагнитных волн и великолепно работающая в диапазоне радиоволн, отказалась объяснять явление фотоэффекта.

Выход из этого тупика был найден Альбертом Эйнштейном в 1905 году. Он нашел простое уравнение, описывающее фотоэффект. Все три закона фотоэффекта оказались следствиями уравнения Эйнштейна.

Главная заслуга Эйнштейна состояла в отказе от попыток истолковать фотоэффект с позиций классической электродинамики. Эйнштейн привлек к делу смелую гипотезу о квантах, высказанную Максом Планком пятью годами ранее.

Уравнение Эйнштейна для фотоэффекта

Гипотеза Планка говорила о дискретности излучения и поглощения электромагнитных волн, то есть о прерывистом характере взаимодействия света с веществом. При этом Планк считал, что распространение света это непрерывный процесс, происходящий в полном соответствии с законами классической электродинамики.

Эйнштейн пошел еще дальше: он предположил, что свет в принципе обладает прерывистой структурой: не только излучение и поглощение, но также и распространение света происходит отдельными порциями квантами, обладающими энергией E = h ν .

Планк рассматривал свою гипотезу лишь как математический трюк и не решился опровергнуть электродинамику применительно к микромиру. Физической реальностью кванты стали благодаря Эйнштейну.

Кванты электромагнитного излучения (в частности, кванты света) стали впоследствии называться фотонами. Таким образом, свет состоит из особых частиц фотонов, движущихся в вакууме со скоростью c . Каждый фотон монохроматического света, имеющего частоту, несет энергию h ν .

Фотоны могут обмениваться энергией и импульсом с частицами вещества; в таком случае мы говорим о столкновении фотона и частицы. В частности, происходит столкновение фотонов с электронами металла катода.

Поглощение света это поглощение фотонов, то есть неупругое столкновение фотонов с частицами (атомами, электронами). Поглощаясь при столкновении с электроном, фотон передает ему свою энергию. В результате электрон получает кинетическую энергию мгновенно, а не постепенно, и именно этим объясняется безынерционность фотоэффекта.

Уравнение Эйнштейна для фотоэффекта есть не что иное, как закон сохранения энергии. На что идет энергия фотона h ν при его неупругом столкновении с электроном? Она расходуется на совершение работы выхода A по извлечению электрона из вещества и на придание электрону кинетической энергии mv 2 /2: h ν = A + mv 2 /2 (4)

Слагаемое mv 2 /2 оказывается максимальной кинетической энергией фотоэлектронов. Почему максимальной? Этот вопрос требует небольшого пояснения.

Электроны в металле могут быть свободными и связанными. Свободные электроны «гуляют» по всему металлу, связанные электроны «сидят» внутри своих атомов. Кроме того, электрон может находиться как вблизи поверхности металла, так и в его глубине.

Ясно, что максимальная кинетическая энергия фотоэлектрона получится в том случае, когда фотон попадет на свободный электрон в поверхностном слое металла тогда для выбивания электрона достаточно одной лишь работы выхода.

Во всех других случаях придется затрачивать дополнительную энергию на вырывание связанного электрона из атома или на «протаскивание» глубинного электрона к поверхности. Эти лишние затраты приведут к тому, что кинетическая энергия вылетевшего электрона окажется меньше.

Замечательное по простоте и физической ясности уравнение (4) содержит в себе всю теорию фотоэффекта:

1. число выбиваемых электронов пропорционально числу поглощенных фотонов. С увеличением интенсивности света количество фотонов, падающих на катод за секунду, возрастает. Стало быть, пропорционально возрастает число поглощенных фотонов и, соответственно, число выбитых за секунду электронов.

2. Выразим из формулы (4) кинетическую энергию: mv 2 /2 = h ν — A

Действительно, кинетическая энергия выбитых электронов линейно растет с частотой и не зависит от интенсивности света.

Зависимость кинетической энергии от частоты имеет вид уравнения прямой, проходящей через точку ( A / h ; 0). Этим полностью объясняется ход графика на рис. 3.

3. Для того, чтобы начался фотоэффект, энергии фотона должно хватить как минимум на совершение работы выхода: h ν > A . Наименьшая частота ν ₀, определяемая равенством

как раз и будет красной границей фотоэффекта. Как видим, красная граница фотоэффекта ν ₀ = A / h определяется только работой выхода, т. е. зависит лишь от вещества облучаемой поверхности катода.

Уравнение Эйнштейна (4) дает возможность экспериментального нахождения постоянной Планка. Для этого надо предварительно определить частоту излучения и работу выхода материала катода, а также измерить кинетическую энергию фотоэлектронов.

В ходе таких опытов было получено значение h , в точности совпадающее с (2). Такое совпадение результатов двух независимых экспериментов на основе спектров теплового излучения и уравнения Эйнштейна для фотоэффекта означало, что обнаружены совершенно новые «правила игры», по которым происходит взаимодействие света и вещества. В этой области классическая физика в лице механики Ньютона и электродинамики Максвелла уступает место квантовой физике теории микромира, построение которой продолжается и сегодня.

Содержание

Фотоэффект. Фотоны
Ток насыщения. Закономерности фотоэффекта
Постоянная Планка. Уравнение Эйнштейна
Физика. 11 класс
🎥 Видео

Видео:Почему E=mc²?Скачать

Фотоэффект. Фотоны

В 1887 году Г. Герцем был открыт фотоэлектрический эффект, а продолжить его исследования довелось А.Г. Столетову. Ф. Леонард в 1900 году серьезно занялся данным проектом. К тому времени был открыт электрон. Это говорило о том, что фотоэффект состоял в вырывании электронов из вещества под действием падающего на него света.

Данное исследование законов Столетова изображено на рисунке 5 . 2 . 1 .

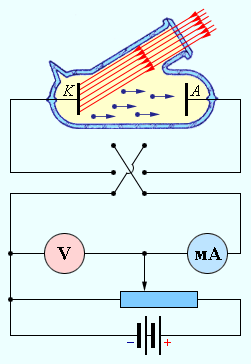
Рисунок 5 . 2 . 1 . Схема экспериментальной установки для изучения фотоэффекта.

В лабораторных условиях применили стеклянный вакуумный баллон с двумя металлическими электродами с очищенной поверхностью. К ним прикладывали напряжение U с возможностью изменения полярности с помощью ключа. Катод освещали монохроматическим светом с длиной волны λ через кварцевое окошко. Так как световой поток оставался неизменным, то зависимость силы тока I от напряжения ослабевала. Рисунок 5 . 2 . 2 . наглядно демонстрирует кривые зависимости при интенсивном свете, попадающем на катод.

Рисунок 5 . 2 . 2 . Зависимость силы фототока от приложенного напряжения. Кривая 2 соответствует большей интенсивности светового потока. I н 1 и I н 2 – токи насыщения, U з – запирающий потенциал.

По графику видно, что при подаче большого напряжения фототок анода А достигает насыщения, потому как при вырывании светом из катода они в состоянии достичь его.

Видео:Решение Шварцшильда уравнений Эйнштейна и его следствияСкачать

Ток насыщения. Закономерности фотоэффекта

Ток насыщения I н прямо пропорционален интенсивности падающего света.

При наличии отрицательного напряжения на аноде, электрическое поле, находящееся между катодом и анодом, тормозится электронами. К аноду могут добраться электроны, у которых кинетическая энергия превышает значение | e U | . При наличии напряжения меньше, чем – U з , происходит прекращение фототока. После измерения – U з определяется максимальная кинетическая энергия фотоэлектронов:

m υ 2 2 m a x = e U 3 .

Из формулы видно, что оно не зависит от интенсивности падающего света. После глубоких исследований стало ясно, что при возрастании запирающего потенциала происходит линейное увеличение частоты света ν .

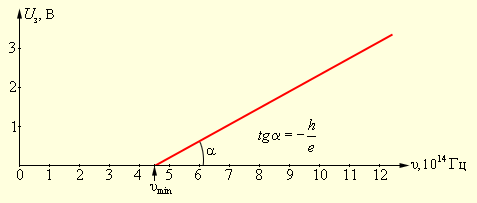
Рисунок 5 . 2 . 3 . Зависимость запирающего потенциала U з от частоты ν падающего света.

После многочисленных экспериментов были установлены закономерности формул фотоэффекта:

При увеличении частоты света ν происходит возрастание кинетической энергии, независящей от ее интенсивности.
Наименьшей частотой ν m i n с внешним фотоэффектом называют красную границу фотоэффекта каждого вещества.
Количество фотоэлектронов за 1 с вырывания из катода прямо пропорционально интенсивности света.
Фотоэффект возникает после освещения катода с условием, что ν > ν m i n _.

Данные закономерности не соответствовали представлениям классической физики о взаимодействии света с веществом. Исходя из волновых представлений, взаимодействие световой волны с электроном должно действовать по принципу постепенного накапливания энергии. Чтобы он смог вылететь из катода, необходимо иметь достаточное количество энергии, накапливаемой за определенный промежуток времени, не зависящий от интенсивности света.

Появление фотоэлектронов происходит сразу после освещения катода. Данная модель не давала четкого представления нахождения красной границы фотоэффекта. Волновая теория света не могла дать объяснение независимости энергии фотоэлектронов от интенсивности светового потока и пропорциональности максимальной кинетической энергии частоты света. Поэтому электромагнитная теория была не способна объяснить эти изменения.

В 1905 году А. Эйнштейн дает теоретическое объяснение наблюдаемых закономерностей фотоэффекта, основываясь на гипотезе М. Планка.

Видео:Относительность 19 - Уравнение ЭйнштейнаСкачать

Постоянная Планка. Уравнение Эйнштейна

Излучение и поглощение света происходит определенными порциями, где она определяется формулой E = h ν , h принято называть постоянной Планка.

Основной шаг в развитии квантовых представлений относится к Эйнштейну:

Свет обладает прерывистой структурой. Электромагнитная волна состоит из порций, называемых, кварками, спустя время которые зафиксировали как фотоны.

После взаимодействия с веществом фотон передает свою энергию h ν одному электрону, одна часть которой рассеивается при столкновениях с атомами, а другая затрачивается на преодоление потенциального барьера на границе металл-вакуум. Для этого ему необходимо совершить работу выхода А , зависящую от свойств материала катода.

Наибольшую кинетическую энергию, вылетевшую из катода фотоэлектроном, определяют законом сохранения энергии:

m ν 2 2 m a x = e U e = h ν — A .

Формула получила название уравнения Эйнштейна для фотоэффекта.

Благодаря ему, закономерности внешнего явления фотоэффекта могут быть объяснены.

Линейная зависимость максимальной кинетической энергии от частоты и независимость от интенсивности света, существование красной границы, безынерционность фотоэффекта следуют из данного выражения.

Общее количество фотоэлектронов, которые покидают поверхность катода в течение 1 с , пропорционально числу фотонов, падающих на поверхность. Можно сделать вывод, что ток насыщения должен быть прямо пропорционален интенсивности светового потока.

По уравнению фотоэффекта Эйнштейна тангенс угла наклона прямой, выражающий зависимость запирающего потенциала U з от частоты ν , равняется отношению постоянной Планка h к заряду электрона e :

Формула позволяет вычислить значение постоянной Планка.

Р. Милликенн проводил измерения в 1914 году, после чего смог определить работу выхода А :

A = h ν m i n = h c λ к р ,

где c – скорость света, λ к р – длина волны, которая соответствует красной границе фотоэффекта.

Большинство металлов имеет работу выхода А и составляет несколько электрон-вольт ( 1 э В = 1 , 602 · 10 – 19 Д ж ) .

Квантовая физика использует электрон-вольт как энергетическую единицу измерения. Тогда значение постоянной Планка равняется

h = 4 , 136 · 10 — 15 э В · с .

Наименьшая работа выхода наблюдается у щелочных элементов. Натрий при A = 1 , 9 э В соответствует красной границе фотоэффекта λ к р ≈ 680 н м . Такие соединения применяют для создания катодов в фотоэлементах, используемых для регистрации видимого света.

Законы фотоэффекта говорят о том, что при пропускании и поглощении свет ведет себя подобно потоку частиц, называемых фотонами или световыми квантами.

Энергия фотонов записывается в виде формулы E = h ν .

При движении в вакууме фотон обладает скоростью с , а его масса m = 0 . Общее соотношение теории относительности, связывающее энергию, импульс и массу любой частицы, записывается как E 2 = m 2 c 4 + p 2 c 2 .

Отсюда следует, что фотон обладает импульсом, значит:

Можно сделать вывод, что учение о свете вернулось к представлениям о световых частицах – корпускулах. Но это не расценивается как возврат к корпускулярной теории Ньютона. В XX было известно о двойственной природе света. Когда он распространялся, то проявлялись его волновые свойства (интерференция, дифракция, поляризация), при его взаимодействии с веществом – корпускулярные, то есть явление фотоэффекта. Это и получило название корпускулярно-волнового дуализма.

Спустя время, данная теория была подтверждена у других элементарных частиц. Классическая физика не дает наглядную модель сочетаний волновых и корпускулярных свойств микрообъектов. Их движениями управляют законы квантовой механики. В основе этой науки лежит теория абсолютно черного тела, доказанная М. Планком, и квантовая, предложенная Эйнштейном.

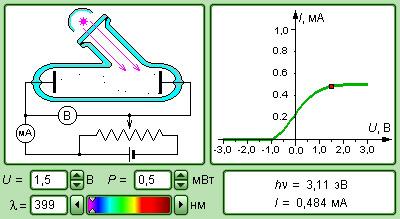
Рисунок 5 . 2 . 4 . Модель фотоэффекта

Видео:Теория относительности для чайников (часть 1)Скачать

Физика. 11 класс

Конспект урока

Физика, 11 класс

Урок 22. Фотоэффект

Перечень вопросов, рассматриваемых на уроке:

предмет и задачи квантовой физики;
гипотеза М. Планка о квантах;
опыты А.Г. Столетова;
определение фотоэффекта, кванта, тока насыщения, задерживающего напряжения, работы выхода, красной границы фотоэффекта;
уравнение Эйнштейна для фотоэффекта;
законы фотоэффекта.

Глоссарий по теме:

Квантовая физика — раздел теоретической физики, в котором изучаются квантово-механические и квантово-полевые системы и законы их движения.

Фотоэффект – это вырывание электронов из вещества под действием света.

Квант — (от лат. quantum — «сколько») — неделимая порция какой-либо величины в физике.

Ток насыщения — некоторое предельное значение силы фототока.

Задерживающее напряжение — минимальное обратное напряжение между анодом и катодом, при котором фототок равен нулю.

Работа выхода – это минимальная энергия, которую надо сообщить электрону, чтобы он покинул металл. которую нужно сообщить электрону, для того чтобы он мог преодолеть силы, удерживающие его внутри металла.

Красная граница фотоэффекта – это минимальная частота или максимальная длина волны света излучения, при которой еще возможен внешний фотоэффект.

Основная и дополнительная литература по теме урока:

1. Мякишев Г. Я., Буховцев Б. Б., Чаругин В. М. Физика. 11 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 259 – 267.

2. Рымкевич А. П. Сборник задач по физике. 10-11 класс.- М.:Дрофа,2009. – С. 153 – 158.

3. Элементарный учебник физики. Учебное пособие в 3 т./под редакцией академика Ландсберга Г. С.: Т.3. Колебания и волны. Оптика. Атомная и ядерная физика. – 12-е изд. – М.: ФИЗМАТЛИТ, 2001. С. 422 – 429.

4. Тульчинский М. Е. Качественные задачи по физике в средней школе. Пособие для учителей. Изд. 4-е, переработ. и доп. М. «Просвещение», 1972. С. 157.

Теоретический материал для самостоятельного изучения

В начале 20-го века в физике произошла величайшая революция. Попытки объяснить наблюдаемые на опытах закономерности распределения энергии в спектрах теплового излучения оказались несостоятельными. Законы электромагнетизма Максвелла неожиданно «забастовали». Противоречия между опытом и практикой были разрешены немецким физиком Максом Планком.

Гипотеза Макса Планка: атомы испускают электромагнитную энергию не непрерывно, а отдельными порциями – квантами. Энергия Е каждой порции прямо пропорциональна частоте ν излучения света: E = hν.

Коэффициент пропорциональности получил название постоянной Планка, и она равна:

h = 6,63 ∙ 10 -34 Дж∙с.

После открытия Планка начала развиваться самая современная и глубокая физическая теория – квантовая физика.

Квантовая физика — раздел теоретической физики, в котором изучаются квантово-механические и квантово-полевые системы и законы их движения.

Поведение всех микрочастиц подчиняется квантовым законам. Но впервые квантовые свойства материи были обнаружены именно при исследовании излучения и поглощения света.

В 1886 году немецкий физик Густав Людвиг Герц обнаружил явление электризации металлов при их освещении.

Явление вырывания электронов из вещества под действием света называется внешним фотоэлектрическим эффектом.

Законы фотоэффекта были установлены в 1888 году профессором московского университета Александром Григорьевичем Столетовым.

Схема установки для изучения законов фотоэффекта

Первый закон фотоэффекта: фототок насыщения — максимальное число фотоэлектронов, вырываемых из вещества за единицу времени, — прямо пропорционален интенсивности падающего излучения.

Зависимость силы тока от приложенного напряжения

Увеличение интенсивности света означает увеличение числа падающих фотонов, которые выбивают с поверхности металла больше электронов.

Второй закон фотоэффекта: максимальная кинетическая энергия фотоэлектронов не зависит от интенсивности падающего излучения и линейно возрастает с увеличением частоты падающего излучения.

Третий закон фотоэффекта: для каждого вещества существует граничная частота такая, что излучение меньшей частоты не вызывает фотоэффекта, какой бы ни была интенсивность падающего излучения. Эта минимальная частота излучения называется красной границей фотоэффекта.

где А_в – работа выхода электронов;

h – постоянная Планка;

ν_min — частота излучения, соответствующая красной границе фотоэффекта;

с – скорость света;

λкр – длина волны, соответствующая красной границе_.

Фотоэффект практически безынерционен: фототок возникает одновременно с освещением катода с точностью до одной миллиардной доли секунды.

Работа выхода – это минимальная энергия, которую надо сообщить электрону, чтобы он покинул металл.

Для большинства веществ фотоэффект возникает только под действием ультрафиолетового облучения. Однако некоторые металлы, например, литий, натрий и калий, испускают электроны и при облучении видимым светом.

Известно, что фототоком можно управлять, подавая на металлические пластины различные напряжения. Если на систему подать небольшое напряжение обратной полярности, «затрудняющее» вылет электронов, то ток уменьшится, так как фотоэлектронам, кроме работы выхода, придется совершать дополнительную работу против сил электрического поля.

Задерживающее напряжение — минимальное обратное напряжение между анодом и катодом, при котором фототок равен нулю.

Максимальная кинетическая энергия электронов выражается через задерживающее напряжение:

где — максимальная кинетическая энергия электронов;

Е – заряд электрона;

– задерживающее напряжение.

Теорию фотоэффекта разработал Альберт Эйнштейн. На основе квантовых представлений Эйнштейн объяснил фотоэффект. Электрон внутри металла после поглощения одного фотона получает порцию энергии и стремится вылететь за пределы кристаллической решетки, т.е. покинуть поверхность твердого тела. При этом часть полученной энергии он израсходует на совершение работы по преодолению сил, удерживающих его внутри вещества. Остаток энергии будет равен кинетической энергии:

В 1921 году Альберт Эйнштейн стал обладателем Нобелевской премии, которая, согласно официальной формулировке, была вручена «за заслуги перед теоретической физикой и особенно за открытие закона фотоэлектрического эффекта».

Если фотоэффект сопровождается вылетом электронов с поверхности вещества, то его называют внешним фотоэффектом или фотоэлектронной эмиссией, а вылетающие электроны — фотоэлектронами. Если фотоэффект не сопровождается вылетом электронов с поверхности вещества, то его называют внутренним.

Примеры и разбор решения заданий

1. Монохроматический свет с длиной волны λ падает на поверхность металла, вызывая фотоэффект. Фотоэлектроны тормозятся электрическим полем. Как изменятся работа выхода электронов с поверхности металла и запирающее напряжение, если уменьшить длину волны падающего света?

Для каждой величины определите соответствующий характер изменения:

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Работа выхода — это характеристика металла, следовательно, работа выхода не изменится при изменении длины волны падающего света.

Запирающее напряжение — это такое минимальное напряжение, при котором фотоэлектроны перестают вылетать из металла. Оно определяется из уравнения:

Следовательно, при уменьшении длины волны падающего света, запирающее напряжение увеличивается.

2. Красная граница фотоэффекта для вещества фотокатода λ₀ = 290 нм. При облучении катода светом с длиной волны λ фототок прекращается при напряжении между анодом и катодом U = 1,5 В. Определите длину волны λ.

Запишем уравнение для фотоэффекта через длину волны:

Условие связи красной границы фотоэффекта и работы выхода:

Запишем выражение для запирающего напряжения – условие равенства максимальной кинетической энергии электрона и изменения его потенциальной энергии при перемещении в электростатическом поле: