Уравнение эйнштейна для энергии и импульса (6 видео)

Три значения самого знаменитого уравнения Эйнштейна

Эйнштейн выводит СТО перед аудиторией; 1934.

Сотни лет в физике присутствовал непреложный закон, в котором никогда не сомневались: в любой реакции, происходящей во Вселенной, сохраняется масса. Неважно, какие ингредиенты использовать, какая реакция произошла, и что получилось – сумма того, с чего вы начинали, и сумма того, с чем вы оказывались, будут равными по массе. Но по законам специальной теории относительности масса не может быть сохраняющейся величиной, поскольку различные наблюдатели не согласятся по поводу того, какой энергией обладает система. Вместо этого Эйнштейн смог вывести закон, который мы используем и по сей день, управляемый одним из простых и наиболее мощных уравнений: E=mc 2 .

Ядерную ракету готовят к испытаниям в 1967. Ракета работает на преобразовании массы в энергию, E = mc 2 .

У самого знаменитого уравнения Эйнштейна всего три составляющих:

E, или энергия, полностью занимающая одну часть уравнения, и представляющая полную энергию системы.
m, масса, связанная с энергией через преобразовательный множитель.
c 2 , квадрат скорости света – нужный фактор, обеспечивающий эквивалентность массы и энергии.

Нильс Бор и Альберт Эйнштейн обсуждают множество тем дома у Пауля Эренфеста в 1925. Дебаты Бора с Эйнштейном были наиболее влиятельным фактором во время разработки квантовой механики. Сегодня Бор наиболее известен своим вкладом в квантовую физику, а Эйнштейн – за вклад в теорию относительности и эквивалентность энергии и массы.

Смысл этого уравнения изменил весь мир. Как писал сам Эйнштейн:

Из специальной теории относительности следовало, что масса и энергия – разные проявления одной вещи. Эта концепция была незнакома среднему человеку.

И вот три самых значимых следствия этого простого уравнения.

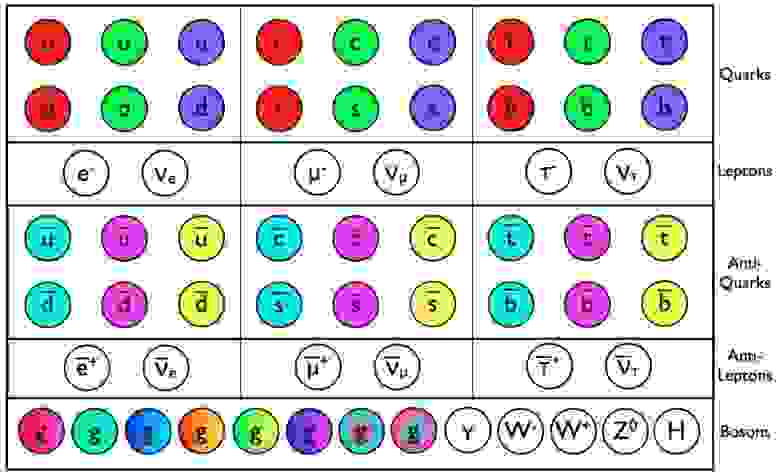
Кварки, антикварки и глюоны Стандартной модели обладают цветным зарядом, в дополнение ко всем другим свойствам вроде массы и электрического заряда. Не имеют массы только глюоны и фотоны; все остальные, даже нейтрино, обладают ненулевой массой покоя.

Даже у покоящихся масс есть присущая им энергия. В школе вы изучали все типы энергий – механическую, химическую, электрическую, кинетическую. Все эти виды энергий присущи движущимся или реагирующим объектам, и эти формы энергии можно использовать для выполнения работы, например, для запуска двигателя, свечения лампочки или перемалывания зерна в муку. Но даже обычная масса покоя обладает присущей ей энергией: и огромным количеством. Это ведёт к потрясающему следствию: гравитация, возникающая между двумя любыми массами в ньютоновой вселенной, тоже должна работать на основании энергии, эквивалентной массе согласно уравнению E = mc 2 .

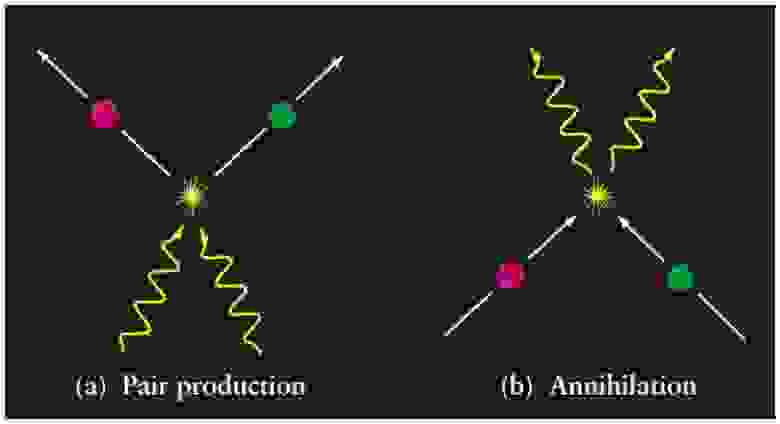
Создание пар частиц из материи/антиматерии из чистой энергии (слева) – реакция полностью обратимая (справа), ведь материя и антиматерия могут аннигилировать, породив чистую энергию. Этот процесс сотворения и аннигиляции подчиняется уравнению E = mc 2 , и является единственным известным способом создания и уничтожения материи и антиматерии.

Массу можно преобразовать в чистую энергию. Это второе значение уравнения, и E = mc 2 сообщает нам, сколько точно энергии можно получить при преобразовании массы. На каждый килограмм массы, превращающейся в энергию, получится 9 × 10 16 Дж энергии, что эквивалентно 21 мегатонн ТНТ. Наблюдая за радиоактивным распадом, или реакциями деления или синтеза ядер, можно видеть, что итоговая масса оказывается меньше начальной; закон сохранения массы не работает. Но разница равняется количеству освобождённой энергии! Это работает для всех случаев, от распада урана и атомных бомб до ядерного синтеза в ядре Солнца и аннигиляции частиц материи/антиматерии. Уничтожаемая масса превращается в энергию, количество которой рассчитывается по формуле E = mc 2 .

Следы частиц, порождаемых высокоэнергетическими столкновениями на Большом адронном коллайдере, 2014. Композитные частицы распадаются на компоненты, которые рассеиваются в пространстве, но также появляются и новые частицы, благодаря энергии, доступной при столкновении.

Энергию можно использовать для создания массы практически из ничего – просто из чистой энергии. Последнее значение формулы наиболее выдающееся. Если взять два бильярдных шара и сильно столкнуть их вместе, то на выходе получится два бильярдных шара. Если взять фотон и электрон и столкнуть их вместе, то получится фотон и электрон. Но если столкнуть их с достаточно большой энергией, то получится фотон, электрон и новая пара частиц материи/антиматерии. Иначе говоря, можно создать две новые массивные частицы:

частицу материи, например, электрон, протон, нейтрон, и т.п.,
частицу антиматерии, например, позитрон, антипротон, антинейтрон и т.п.

которые появятся, только если вложить в эксперимент достаточно энергии. Именно так на ускорителях, таких, как БАК в ЦЕРН, ищут новые, нестабильные высокоэнергетические частицы (такие, как бозон Хиггса или верхний кварк): создавая новые частицы из чистой энергии. Получающаяся масса возникает из доступной энергии: m = E/c 2 . Это также означает, что время жизни частицы ограничено, то из-за принципа неопределённости Гейзенберга ей присуща неопределённость значения массы, поскольку δE δt

ℏ, и, следовательно, из уравнения Эйнштейна следует и соответствующая δm. Когда физики рассуждают о ширине частицы, они имеют в виду эту внутреннюю неопределённость массы.

Искривление пространства-времени гравитационными массами в картине мира ОТО

Эквивалентность энергии и массы также привела Эйнштейна к такому великому достижению, как общая теория относительности. Представьте, что у вас имеется частица материи и частица антиматерии, с одинаковыми массами покоя. Их можно аннигилировать, и они превратятся в фотоны с определённой энергией, точно по формуле E = mc 2 . Теперь представьте, что эта пара частица/античастица быстро двигается, будто бы упав к нам из глубокого космоса, а затем аннигилирует вблизи поверхности Земли. У этих фотонов окажется дополнительная энергия – не только E из E = mc 2 , но и дополнительная E, кинетическая энергия, приобретённая из-за падения.

Если два объекта из материи и антиматерии, находясь в покое, аннигилируют, они превратятся в фотоны совершенно определённой энергии. Если эти фотоны появятся после падения в гравитационном поле, энергия у них будет выше. Значит, должно существовать гравитационное красное или синее смещение, не предсказанное гравитацией Ньютона – иначе энергия бы не сохранялась.

Если энергия должна сохраняться, то гравитационное красное (и синее) смещения должны быть реальными. У гравитации Ньютона нет способа объяснить этот эффект, но в Эйнштейновской ОТО кривизна пространства означает, что падение в гравитационное поле добавляет вам энергии, а выход из гравитационного поля заставляет вас тратить энергию. Получается, что полная и общая взаимосвязь для любого движущегося объекта будет не E = mc 2 , а E 2 = m 2 c 4 + p 2 c 2 (где p – импульс). И только обобщая всю информацию, включая в описание энергию, импульс и гравитацию, можно по-настоящему описать Вселенную.

Когда квант излучения покидает гравитационное поле, его частота испытывает красное смещение из-за сохранения энергии; когда он падает в поле, он должен испытывать синее смещение. А это имеет смысл, только если гравитация связана не только с массой, но и с энергией.

Величайшее уравнение Эйнштейна, E = mc 2 , является триумфом мощи и простоты фундаментальной физики. У материи есть присущая ей энергия, массу можно превратить (при определённых условиях) в чистую энергию, а энергию можно использовать для создания массивных объектов, не существовавших ранее. Такой метод размышлений даёт нам возможность открывать фундаментальные частицы, из которых состоит наша Вселенная, изобретать ядерную энергию и ядерное оружие, открывать теорию гравитации, описывающую взаимодействие всех объектов во Вселенной. Ключом к нахождению этого уравнения послужил скромный мысленный эксперимент, основанный на простом предположении: сохранении энергии и импульса. Остальное оказывается неизбежным следствием схемы работы Вселенной.

Содержание

Релятивистская динамика
Релятивистская энергия
Релятивистский импульс.
Связь энергии и импульса.
Релятивистское уравнение движения.
Уравнения Эйнштейна
💡 Видео

Видео:Что на самом деле значит E=mc²?Скачать

Релятивистская динамика

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: полная энергия, связь массы и энергии, энергия покоя.

В классической динамике мы начали с законов Ньютона, потом перешли к импульсу, а после него — к энергии. Здесь мы ради простоты изложения поступим ровно наоборот: начнём с энергии, затем перейдём к импульсу и закончим релятивистским уравнением движения — модификацией второго закона Ньютона для теории относительности.

Видео:Относительность 19 - Уравнение ЭйнштейнаСкачать

Релятивистская энергия

Предположим, что изолированное тело массы покоится в данной системе отсчёта. Одно из самых впечатляющих достижений теории относительности — это знаменитая формула Эйнштейна:

Здесь — энергия тела, — скорость света в вакууме. Поскольку тело покоится, энергия , вычиляемая по формуле (1) , называется энергией покоя.

Формула (1) утверждает, что каждое тело само по себе обладает энергией — просто потому, что оно существует в природе. Образно говоря, природа затратила определённые усилия на то, чтобы «собрать» данное тело из мельчайших частиц вещества, и мерой этих усилий служит энергия покоя тела. Энергия эта весьма велика; так, в одном килограмме вещества заключена энергия

Интересно, какое количество топлива нужно сжечь, чтобы выделилось столько энергии? Возьмём, например, дерево. Его удельная теплота сгорания равна Дж/кг, поэтому находим: кг . Это девять миллионов тонн!

Ещё для сравнения: такую энергию единая энергосистема России вырабатывает примерно за десять дней.

Почему столь грандиозная энергия, содержащаяся в теле, до сих пор оставалась нами незамеченной? Почему в нерелятивистских задачах, связанных с сохранением и превращением энергии, мы не учитывали энергию покоя? Скоро мы ответим на этот вопрос.

Поскольку энергия покоя тела прямо пропорциональна его массе, изменение энергии покоя на величину приводит к изменению массы тела на

Так, при нагревании тела возрастает его внутренняя энергия, и, стало быть, масса тела увеличивается! В повседневной жизни мы не замечаем этого эффекта ввиду его чрезвычайной малости. Например, для нагревания воды массой кг на (удельная теплоёмкость воды равна ) ей нужно передать количество теплоты:

Увеличение массы воды будет равно:

Столь ничтожное изменение массы невозможно заметить на фоне погрешностей измерительных приборов.

Формула ( 1 ) даёт энергию покоящегося тела. Что изменится, если тело движется?

Снова рассмотрим неподвижную систему отсчёта и систему , движущуюся относительно со скоростью . Пусть тело массы покоится в системе ; тогда энергия тела в системе есть энергия покоя, вычисляемая по формуле ( 1 ). Оказывается, при переходе в систему энергия преобразуется так же, как и время — а именно, энергия тела в системе , в которой тело движется со скоростью , равна:

Формула ( 2 ) была также установлена Эйнштейном. Величина — это полная энергия движущегося тела. Поскольку в данной формуле делится на «релятивистский корень», меньший единицы, полная энергия движущегося тела превышает энергию покоя. Полная энергия будет равна энергии покоя только при .

Выражение для полной энергии ( 2 ) позволяет сделать важные выводы о возможных скоростях движения объектов в природе.

1. Каждое массивное тело обладает определённой энергией, поэтому необходимо выполнение неравенства

Оно означает, что : скорость массивного тела всегда меньше скорости света.

2. В природе существуют безмассовые частицы (например, фотоны), несущие энергию. При подстановке в формулу ( 2 ) её числитель обращается в нуль. Но энергия-то фотона ненулевая!

Единственный способ избежать здесь противоречия — это принять, что безмассовая частица обязана двигаться со скоростью света. Тогда и знаменатель нашей формулы обратится в нуль, так что формула ( 2 ) попросту откажет. Нахождение формул для энергии безмассовых частиц не входит в компетенцию теории относительности. Так, выражение для энергии фотона устанавливается в квантовой физике.

Интуитивно чувствуется, что полная энергия ( 2 ) состоит из энергии покоя и собственно «энергии движения», т. е. кинетической энергии тела. При малых скоростях движения это показывается явным образом. Используем приближённые формулы, справедливые при :

С помощью этих формул последовательно получаем из ( 2 ):

Таким образом, при малых скоростях движения полная энергия сводится просто к сумме энергия покоя и кинетической энергии. Это служит мотивировкой для определения понятия кинетической энергии в теории относительности:

При формула ( 6 ) переходит в нерелятивистское выражение .

Теперь мы можем ответить на заданный выше вопрос о том, почему до сих пор не учитывалась энергия покоя в нерелятивистских энергетических соотношениях. Как видно из ( 5 ), при малых скоростях движения энергия покоя входит в полную энергию в качестве слагаемого. В задачах, например, механики и термодинамики изменения энергии тел составляют максимум несколько миллионов джоулей; эти изменения столь незначительны по сравнению с энергиями покоя рассматриваемых тел, что приводят к микроскопическим изменениям их масс. Поэтому с высокой точностью можно считать, что суммарная масса тел не меняется в ходе механических или тепловых процессов. В результате суммы энергий покоя тел в начале и в конце процесса попросту сокращаются в обеих частях закона сохранения энергии!

Но такое бывает не всегда. В других физических ситуациях изменения энергии тел могут приводить к более заметным изменениям суммарной массы. Мы увидим, например, что в ядерных реакциях отличия масс исходных и конечных продуктов обычно составляют доли процента.Скажем, при распаде ядра урана суммарная масса продуктов распада примерно на меньше массы исходного ядра. Эта одна тысячная доля массы ядра высвобождается в виде энергии, которая при взрыве атомной бомбы способна уничтожить город.

При неупругом столкновении часть кинетической энергии тел переходит в их внутренюю энергию. Релятивистский закон сохранения полной энергии учитывает этот факт: суммарная масса тел после столкновения увеличивается!

Рассмотрим в качестве примера два тела массы , летящих навстречу друг другу с одинаковой скоростью . В результате неупругого столкновения образуется тело массы , скорость которого равна нулю по закону сохранения импульса (об этом законе речь впереди). Согласно закону сохранения энергии получаем:

Мы видим, что, 2m’ alt=’M> 2m’ /> — масса образовавшегося тела превышает сумму масс тел до столкновения. Избыток массы, равный , возник за счёт перехода кинетической энергии сталкивающихся тел во внутреннюю энергию.

Видео:Почему E=mc²?Скачать

Релятивистский импульс.

Классическое выражение для импульса не годится в теории относительности — оно, в частности, не согласуется с релятивистским законом сложения скоростей. Давайте убедимся в этом на следующем простом примере.

Пусть система движется относительно системы со скоростью (рис. 1 ). Два тела массы в системе летят навстречу друг другу с одинаковой скоростью . Происходит неупругое столкновение.

Уравнение эйнштейна для энергии и импульса

Рис. 1. К закону сохранения импульса

В системе тела после столкновения останавливаются. Давайте, как и выше, найдём массу образовавшегося тела:

Теперь посмотрим на процесс столкновения с точки зрения системы . До столкновения левое тело имеет скорость:

Правое тело имеет скорость:

Нерелятивистский импульс нашей системы до столкновения равен:

После столкновения получившееся тело массы двигается со скоростью .
Его нерелятивистский импульс равен:

Как видим, , то есть нерелятивистский импульс не сохраняется.

Оказывается, правильное выражение для импульса в теории относительности получается делением классического выражения на «релятивистский корень»: импульс тела массы , двигающегося со скоростью , равен:

Давайте вернёмся к только что рассмотренному примеру и убедимся, что теперь с законом сохранения импульса всё будет в порядке.

Импульс системы до столкновения:

Импульс после столкновения:

Вот теперь всё правильно: !

Видео:Урок 104. Импульс. Закон сохранения импульсаСкачать

Связь энергии и импульса.

Из формул ( 2 ) и ( 7 ) можно получить замечательное соотношение между энергией и импульсом в теории относительности. Возводим обе части этих формул в квадрат:

Это и есть искомое соотношение:

Данная формула позволяет выявить простую связь между энергией и импульсом фотона. Фотон имеет нулевую массу и движется со скоростью света. Как уже было замечено выше, сами по себе энергия и импульс фотона в СТО найдены быть не могут: при подстановке в формулы ( 2 ) и ( 7 ) значений и мы получим нули в числителе и знаменателе. Но зато с помощью ( 8 ) легко находим: , или

В квантовой физике устанавливается выражение для энергии фотона, после чего с помощью формулы ( 9 ) находится его импульс.

Видео:Физика - импульс и закон сохранения импульсаСкачать

Релятивистское уравнение движения.

Рассмотрим тело массы , движущееся вдоль оси под действием силы . Уравнение движения тела в классической механике — это второй закон Ньютона: . Если за бесконечно малое время приращение скорости тела равно , то , и уравнение движения запишется в виде:

Теперь заметим, что — изменение нерелятивистского импульса тела. В результате получим «импульсную» форму записи второго закона Ньютона — производная импульса тела по времени равна силе, приложенной к телу:

Все эти вещи вам знакомы, но повторить никогда не помешает 😉

Классическое уравнение движения — второй закон Ньютона — является инвариантным относительно преобразований Галилея, которые в классической механике описывают переход из одной инерциальной системы отсчёта в другую (это означает, напомним, что при указанном переходе второй закон Ньютона сохраняет свой вид). Однако в СТО переход между инерциальными системами отсчёта описывается преобразованиями Лоренца, а относительно них второй закон Ньютона уже не является инвариантным. Следовательно, классическое уравнение движения должно быть заменено релятивистским, которое сохраняет свой вид под действием преобразований Лоренца.

То, что второй закон Ньютона ( 10 ) не может быть верным в СТО, хорошо видно на следующем простом примере. Допустим, что к телу приложена постоянная сила. Тогда согласно классической механике тело будет двигаться с постоянным ускорением; скорость тела будет линейно возрастать и с течением времени превысит скорость света. Но мы знаем, что на самом
деле это невозможно.

Правильное уравнение движения в теории относительности оказывается совсем не сложным.
Релятивистское уравнение движения имеет вид ( 11 ), где p — релятивистский импульс:

Производная релятивистского импульса по времени равна силе, приложенной к телу.

В теории относительности уравнение ( 12 ) приходит на смену второму закону Ньютона.

Давайте выясним, как же в действительности будет двигаться тело массы m под действием постоянной силы . При условии из формулы ( 12 ) получаем:

Остаётся выразить отсюда скорость:

Посмотрим, что даёт эта формула при малых и при больших временах движения.
Пользуемся приближёнными соотношениями при :

Формулы ( 14 ) и ( 15 ) отличаются от формул ( 3 ) и ( 4 ) только лишь знаком в левых частях. Очень рекомендую вам запомнить все эти четыре приближённых равенства — они часто используются в физике.

Итак, начинаем с малых времён движения. Преобразуем выражение ( 13 ) следующим образом:

При малых имеем:

Последовательно пользуясь нашими приближёнными формулами, получим:

Выражение в скобках почти не отличается от единицы, поэтому при малых имеем:

Здесь — ускорение тела. Мы получили результат, хорошо известный нам из классической механики: скорость тела линейно растёт со временем. Это и не удивительно — при малых временах движения скорость тела также невелика, поэтому мы можем пренебречь релятивистскими эффектами и пользоваться обычной механикой Ньютона.

Теперь переходим к большим временам. Преобразуем формулу ( 13 ) по-другому:

При больших значениях имеем:

Хорошо видно, что при скорость тела неуклонно приближается к скорости света , но всегда остаётся меньше — как того и требует теория относительности.

Зависимость скорости тела от времени, даваемая формулой ( 13 ), графически представлена на рис. 2 .

Рис. 2. Разгон тела под действием постоянной силы

Начальный участок графика — почти линейный; здесь пока работает классическая механика. Впоследствии сказываются релятивистские поправки, график искривляется, и при больших временах наша кривая асимптотически приближается к прямой .

Видео:Урок 434. Фотоэффект. Законы фотоэффектаСкачать

Уравнения Эйнштейна

Десять лет понадобилось Эйнштейну чтобы обобщить специальную теорию относительности (1905 г.) до общей теории относительности (1916 г.). Принцип эквивалентности позволил осознать, что гравитация как-то связана с искривлением самого пространства-времени. Кульминацией усилий по точной количественной формулировке данного факта являются уравнения Эйнштейна:

Они записаны с помощью математики, никогда прежде не появлявшейся в уравнениях физики — Римановой геометрии. Буквы с индексами есть не что иное как тензоры: ( displaystyle R_) — тензор Риччи, ( displaystyle g_) — метрический тензор, ( displaystyle T_) — тензор энергии-импульса. Само тензорное исчисление появилось всего несколькими годами ранее теории относительности.

Индексы ( displaystylemu ) и ( displaystyle nu) в уравнениях Эйнштейна могут принимать значения от единицы до четырех, соответственно тензоры можно представить матрицами 4х4. Поскольку они симметричны относительно диагонали, независимы друг от друга оказываются только десять компонент. Таким образом, в развернутом виде имеем систему из десяти нелинейных дифференциальных уравнений — уравнений Эйнштейна.

Задачей решения уравнений Эйнштейна является нахождение явного вида метрического тензора ( displaystyle g_), полностью характеризующего геометрию пространства-времени. Исходными данными являются тензор энергии-импульса ( displaystyle T_) и начальные/граничные условия. Тензор Риччи ( displaystyle R_) и скалярная кривизна Гаусса ( displaystyle R) являются функциями метрического тензора и его производных и характеризуют кривизну пространства-времени. Концептуально уравнения Эйнштейна можно представить как:

геометрия (левая часть) = энергия (правая часть)

Правая часть уравнений Эйнштейна это начальные условия в виде распределения масс (помним, ( displaystyle E=mc^)), а левая это чисто геометрические величины. То есть уравнения говорят, что масса (энергия) влияет на геометрию пространства-времени.

Искривленная геометрия в свою очередь определяет траектории движения материальных тел. То есть согласно Эйнштейну — гравитация это и есть пространство-время. Просто оно в отличие от Ньютоновской теории не является статическим неизменным объектом, а может деформироваться, искривляться.

Метрический тензор — решение уравнений Эйнштейна — в общем случае разный в разных точках пространства, то есть является функцией координат. По-сути само пространство-время становится динамическим объектом (полем), аналогично другим физическим величинам типа электромагнитного поля.

Внешне уравнения Эйнштейна совсем не похожи на закон всемирного тяготения Ньютона:

Но в приближении малых масс и скоростей они повторяют результаты Ньютоновской теории. Из-за множества тензорных компонент аналитические вычисления крайне запутаны, благо сейчас все моделирование можно производить на компьютере.

В рамках ОТО существуют эффекты отсутствующие в Ньютоновской гравитации, например, увлечение систем отсчета вблизи вращающихся массивных тел или недавно экспериментально обнаруженные гравитационные волны.

Гравитация остается единственным полем для которого так и не построена соответствующая квантовая теория. Даже для кварков (составляющих нейтронов и протонов), теоретически предсказанных только в 1960-х, уже давно построена квантовая теория поля.

Это объясняется тем, что все физические величины обычно выражаются в виде функций от пространственных координат и времени ( displaystyle x=f(t)). Что делать когда само пространство ( displaystyle x) и время ( displaystyle t) теряют классический смысл? По-сути стоит задача построить квантовую теорию самого пространства-времени. Наивные подходы, вводящие минимальную длину и минимальный промежуток времени, несостоятельны вследствие относительности этих величин (изменении при преобразованиях Лоренца).

Среди физиков бытует мнение, что квантовая механика более тесно связана с гравитацией чем предполагалось ранее и их объединение приведет к качественно новой теории.