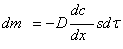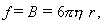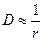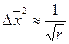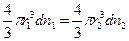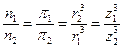3. Диффузия. Ее практическое значение. Уравнение Эйнштейна. Связь между средним сдвигом и коэффициентом диффузии. Уравнение Фика
Диффузией называют самопроизвольный процесс выравнивания концентрации частиц по всему объему раствора или газа под влиянием броуновского движения.
Процесс диффузии идет самопроизвольно, поскольку он сопровождается увеличением энтропии системы. Равномерное распределение вещества в системе отвечает наиболее вероятному ее состоянию.
Часто за причину диффузии принимают осмотическое давление. Это представление было развито Нернстом (1885 г.). Так как осмотическое давление может проявляться лишь при наличии полунепроницаемой перегородки, то это давление бессмысленно рассматривать как какую-то реальную силу, существующую вне связи с мембраной. Тем не менее, осмотическое давление, являющееся также результатом хаотического движения молекул, иногда удобно принимать за причину диффузии.
Перенос массы в результате диффузии сходен с закономерностями переноса тепла или электричества – это легло в основу первого закона диффузии (Фик, 1855г.).
где 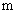
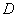
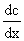
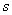
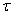
Знак минус перед правой частью уравнения, так как с увеличением значений 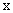
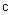
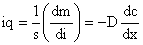
где 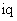
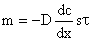
Принимая 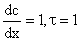
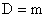
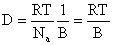
Это уравнение Эйнштейна. Для частиц, по форме близких к сферическим, 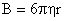
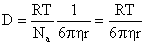
где 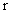
Так как существует связь между броуновским движением и диффузией, то должна существовать связь между средним квадратичным значением проекции смещения частицы 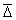
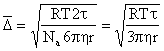
Пользуясь уравнением Эйнштейна-Смолуховского и, зная 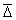
Теория броуновского движения, созданная Эйнштейном и Смолуховским, подтвердила реальное существование молекул. Исследование броуновского движения привело к созданию теории флуктуации и способствовало развитию статической физики.
Флуктуации представляют собой спонтанные отклонения какого-нибудь параметра от среднего равновесного значения в достаточно малых объемах системы. Флуктуация представляет собой явление как бы обратное явлению диффузии.
4. Гипсометрический закон Лапласа
Уравнение Лапласа носит название гипсометрического закона.
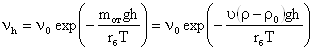
Этот закон был экспериментально подтвержден Перреном (1910г.). Изучая распределение монодисперсной суспензии гуммигута, он использовал уравнение Лапласа для определения числа Авогадро, которое оказалось равным 6,82*10 23 (точное значение 6,024*10 23 ). Гипсометрический закон соблюдается и в аэрозолях, частицы которых имеют небольшую плотность и размер не более 0,05мкм.
Этому закону подчиняется распределение газа по высоте:
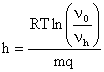
С помощью этой формулы удобно вычислять для любой свободнодисперсной системы величину 
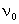

5 Кинетическая или седиментационная устойчивость коллоидно-дисперсных систем. Седиментационый анализ. Вывод уравнения радиуса частиц. Кривые распределения. Монодисперсность и полидисперсность. Методы седиментационного анализа (в поле земного тяготения, в поле центробежной силы – центрифугирование). Их практическое значение
Способность дисперсной системы сохранять равномерное распределение частиц по всему объему принято называть седиментационной, или кинетической устойчивостью системы.
Принцип седиментационного метода анализа дисперсности состоит в измерении скорости осаждения частиц, обычно в жидкой среде. По скорости осаждения частиц с помощью соответствующих уравнений рассчитывают размеры частиц.
Метод позволяет определить распределение частиц по размерам и соответственно подсчитать их удельную поверхность.
Размер частицы дисперсной фазы обычно характеризуют радиусом частицы, реже объемом или площадью ее поверхности. Радиус однозначно определяется только для частиц сферической формы.
В монодисперсной системе все частицы осаждаются с одинаковой скоростью. В соответствии с этим такую же скорость перемещения имеет граница осветления, концентрация частиц по уменьшающейся высоте столба суспензии сохраняется постоянной и также с постоянной скоростью увеличивается масса осевших частиц. Если 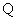
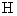
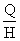
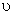
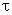
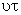
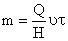
Это уравнение описывает кинетику седиментации в монодисперсной системе. Если принять, что частицы имеют сферическую форму и при их осаждении соблюдается закон Стокса, то, используя формулу:

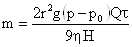
Отсюда радиус частицы равен
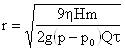
Следовательно, определяя экспериментально зависимость массы осевшего осадка от времени, можно рассчитать размер частиц.
Определение дисперсного состава суспензий, порошков, аэрозолей и других микрогетерогенных систем основано на разнообразных седиментометрических методах дисперсионного анализа.
К ним относят: отмучивание – разделение суспензии на фракции путем многократного отстаивания и сливания; измерение плотности столба суспензии, изменяющейся вследствие седиментации частиц суспензии; пофракционное (дробное) оседание; метод отбора массовых проб – один из наиболее достоверных; накопление осадка на чашке весов; электрофотоседиментометрия, основанная на изменении интенсивности пучка света, проходящего через столб суспензии, о чем судят по измерениям оптической плотности; седиментометрия в поле центробежных сил, основанная на применении центрифуг.
Для успешного проведения седиментометрического анализа должно выполняться условие независимого движения каждой частицы. Этого достигают, применяя разбавленные системы, а в некоторых случаях добавляя стабилизаторы, препятствующие слипанию частиц.
Известны и применяются в практике различные приборы – седиментометры. Например, ряд приборов позволяет проводить анализ по методу накопления осадка на чашечке весов (метод предложен Оденом). Принцип метода состоит в том, что через определенные интервалы времени взвешивают чашку, опущенную в суспензию, и по нарастанию ее массы судят о соотношении различных фракций в суспензии.
Широкое применение для взвешивания чашки с осадком получили торсионные весы. Проведение седиментометрического анализа основано на том, что по мере оседания частиц их масса на чашке увеличивается вначале быстро, так как, прежде всего, оседают наиболее тяжелые частицы, затем все медленнее. При этом каждая фракция считается монодисперсной.
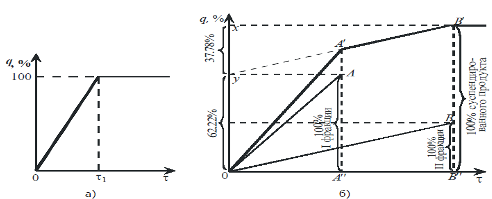
По данным взвешивания осадка получают кривую седиментации, которая выражает зависимость количества осадка q от времени осаждения 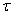
Точка перегиба позволяет определить время полного оседания суспензии 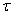
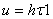
Для бидисперсной системы седиментационная кривая имеет более сложный вид (рис. 1, б). Можно представить себе, что частицы каждой из двух фракций, выпадающие с постоянной скоростью, дают две прямых OA и OB, с различными угловыми коэффициентами, в соответствии с размерами частиц и концентрацией каждой фракции. Однако при совместном оседании обеих фракций мы наблюдаем не эти прямые в отдельности, а суммарную линию седиментации, тангенс угла наклона которой к оси абсцисс является суммой тангенсов углов наклона обеих прямых (OA и OB). В момент полного выпадения фракции, состоящей из частиц больших размеров, эта суммарная линия получает излом (в точке A/) и далее идет параллельно прямой OB, выражающей скорость оседания частиц фракции меньших размеров. В момент окончания оседания второй фракции на графике в точке B/ обнаруживается второй излом, после которого прямая идет параллельно оси абсцисс.
По кривой седиментации оказывается возможным построить прямые осаждения для каждой фракции в отдельности, которые, как было уже сказано, не могут быть получены непосредственно на опыте.
Из рис. 1, б видно, что, продолжая отрезок A/B/ линии седиментации до пересечения с осью ординат и проводя из точки пересечения y прямую, параллельную оси абсцисс, до пересечения ее с линией A/A// , мы получим конечную точку A прямой осаждения фракции, состоящей из крупных частиц. Проводя из начала координат линию OB, параллельную линии y B/ , до пересечения с линией B/B// , получим прямую осаждения фракции, состоящей из мелких частиц, с конечной точкой B .
Рис.1 Кривые седиментации монодисперсной (а) и полидисперсных (б, в) систем.
Если ординаты конечных точек A и B прямых осаждения обеих фракций выражают общее количество (по массе) этих фракций, то очевидно, что ордината точки B/ суммарной линии выражает общее количество обеих фракций (100 %) суспендированного вещества. Легко понять, что отрезки Oy и yx дают относительное содержание каждой фракции в процентах от общего количества суспендированного вещества.
Имеются графические и аналитические методы расчета кривой седиментации.
Монодисперсная система – это система, которая состоит из одинаковых по размеру частиц.
Полидисперсная система – это система, частицы которой имеют различные радиусы.
Так как коллоидные частицы под действием силы тяжести не седиментируют, то под действием центрифуги с большим ускорением можно заставить оседать достаточно быстро и коллоидные частицы.
Ультрацентрифугу используют для определения размера частиц.
Видео:Опыты Столетова. Законы фотоэффекта. Уравнение ЭйнштейнаСкачать

2.3. Молекулярно-кинетические свойства дисперсных систем
2.3.1. Основы теории диффузии
Диффузия – это самопроизвольный процесс выравнивания концентрации частиц во всем объеме коллоидной системы или молекул в растворах.
Еще Т. Грэм в 1861 г. показал, что коллоидные частицы диффундируют гораздо медленнее, чем молекулы в истинных растворах низкомолекулярных веществ. Позднее было установлено, что причиной этой характерной особенности лиозолей является большой размер коллоидных частиц по сравнению с молекулами. Со временем, после разработки точных приборов для определения концентрации дисперсной фазы, измерение коэффициента диффузии частиц в лиозолях превратилось в один из основных методов коллоидной химии, предназначенных для определения размеров частиц дисперсной фазы.
Во всех случаях диффузия идет из слоя золя с более высокой концентрацией частиц до полного выравнивания их концентраций во всех частях системы. Если обозначить dm количество вещества, перенесенного через сечение S по направлению x за время dt, то в соответствии с первым законом А. Фика (1855 г.)
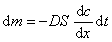
где D – коэффициент диффузии; dc/dx – градиент концентрации.
Знак «минус» показывает, что процесс идет в сторону уменьшения концентрации.
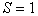
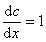
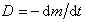
т.е. коэффициент диффузии — это масса вещества, продиффундировавшего за единицу времени через единицу площади при градиенте концентрации, равном единице.
Закон Фика приобретает особенно простой вид, если ввести понятие диффузионного потока, определяемого как количество вещества, перенесенного за единицу времени через сечение, равное единице, т.е.
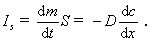
Из входящих в закон Фика величин только одна зависит от свойств диспергированного вещества и дисперсионной среды – это коэффициент диффузии D.
Диффузия очень медленный процесс, поэтому D также мал. Наиболее высокие значения D присущи газам, подвижность частиц которых наибольшая.
Коэффициент диффузии коллоидных частиц определяется из уравнения Эйнштейна
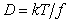
Для сферических несжимаемых частиц, движущихся бесконечно медленно с постоянной скоростью в непрерывной несжимаемой среде так, что жидкость не скользит на поверхности частиц, по закону Стокса

где h – вязкость среды; r – радиус частиц.
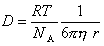
Из этого уравнения, полученного Эйнштейном в 1905 г., видно, что коэффициент диффузии D и скорость диффузии dm/dt не зависят от массы частиц, так как она (масса) не входит в эти уравнения, но зависят от размеров частиц.
Пользуясь уравнением Эйнштейна, можно определить радиус частиц:
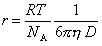
Впервые, используя это уравнение, Ж.Б. Перрен определил «молекулярно-частичную» массу коллоидов.
Так как 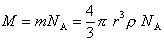
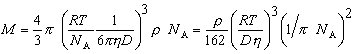

Перрен использовал это уравнение для определения молекулярной массы ряда веществ в истинных растворах и получил достаточно хорошо согласующиеся с теоретическими данными результаты. Таким образом, он доказал, что закон Стокса применим и к молекулярным системам. Однако «молекулярно-частичная» масса коллоидов по этой формуле определяется гораздо точнее, чем молекулярная масса веществ в истинных растворах.
Если рассматривать диффузию частиц в аэрозолях, то оказывается, что закон Стокса в некоторых случаях неприменим, поэтому в уравнение для коэффициентов диффузии необходимо вводить поправки.
Постоянная Стокса В для частиц в аэрозолях меняется в зависимости от размера частиц r:
Видео:Относительность 19 - Уравнение ЭйнштейнаСкачать

Диффузия
Вследствие молекулярно-кинетического движения частицы испытывают случайные смещения, при которых перемещаются вверх или вниз.
Диффузия – самопроизвольно протекающий в системе процесс выравнивания концентраций молекул, ионов или коллоидных частиц под влиянием их хаотического теплового движения.
В термодинамическом отношении процесс диффузии идёт с увеличением энтропии и является самопроизвольным. Явление диффузии необратимо и протекает до полного выравнивания концентраций.
Скорость диффузии при постоянных температуре и вязкости среды (t=const и η=const) зависит только от величины и формы частиц.
Медленность диффузии является признаком, отличающим коллоидные системы от истинных растворов низкомолекулярных веществ.
Перенос массы в результате диффузии формально сходен с законом переноса тепла и электричества. Воспользовавшись этой аналогией, Фик сформулировал (1855г.) первый закон диффузии:
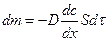
где m — количество продиффундировавшего вещества (моль);
D – коэффициент диффузии, зависит от свойств диффундирующих частиц и среды (м 2 /с);
dc/dx — градиент концентрации (моль/л);
S – площадь, через которую идет диффузия;
τ – продолжительность диффузии;
«-» так как диффузионный поток проходит в направлении меньших концентраций.
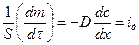
где iд –диффузионный поток, характеризует количество вещества, переносимое в результате диффузии за единицу времени через сечение, равное единице площади.
Принимая dс/dx =1, и S=1, τ=1, тогда получим
т.е. коэффициент диффузии (D) численно равен количеству вещества продиффундировавшего через единицу площади за единицу времени, при градиенте концентрации равном единице.
А. Эйнштейн, изучая броуновское движение, установил связь коэффициента диффузии D со средним сдвигом 

что дает возможность экспериментально установить коэффициент диффузии по методу сдвига.
Рассматривая силы трения, действующую со стороны растворителя на диффузию молекул растворенного вещества, Эйнштейн предложил:
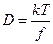
где f – коэффициент трения для растворённых молекул (Нс/м); k – постоянная Больцмана.
С другой стороны, частица со стороны растворителя испытывает силу трения или сопротивление, равное
f= 6 πηr – закон Стокса,
где η – вязкость растворителя, r – радиус частицы.
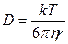
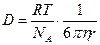
для сферических частиц.
Это уравнение – одно из уравнений коллоидной химии, позволяет определить размер частиц:
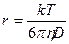
отсюда молекулярный вес: 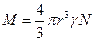
Уравнение Эйнштейна-Стокса выражает физический смысл коэффициента диффузии. Величина kT – мера тепловой или кинетической энергии молекулы, η – мера вязкого сопротивления диффузии. Отношение kT и η определяет насколько легко частица диффундирует. Из уравнения Эйнштейна-Стокса следует, что D обратно пропорционально радиусу,

Рис. 26. Схема, поясняющая понятие осмотического давления.
Перегородка – непроницаемая мембрана для коллоидных частиц (рис. 26). Наличие мембраны ограничивает свободное движение коллоидных частиц в сторону чистой жидкости. Различие в концентрации раствора по обе стороны мембраны не может выровняться путём свободной диффузии. Растворитель переходит в раствор до тех пор, пока этот переход не компенсируется встречно направленным гидростатическим давлением со стороны раствора, это и есть осмотическое давление раствора π.
Осмотическое давление увеличивается из-за перехода части растворителя в сравнении с первоначальным.
Осмотическое давление для разбавленных коллоидных растворов находиться из уравнения:
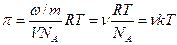
где ω – количество растворенного вещества;
m – масса частицы;
V – объем системы;
ν — частичная концентрация.
Это уравнение аналогично уравнению Вант-Гоффа для осмотического давления истинных растворов:
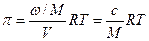
где М – молекулярный вес; с – весовая концентрация.
Осмотическое давление для лиозолей очень маленькая величина и непостоянная, т.к. большие количественные различия в значениях концентрации приводят к слабому проявлению осмоса.
Определим количественную зависимость осмотического давления π от числа частиц n среднего радиуса r и степенью дисперсности z в единице объёма: имеем две дисперсные системы с одинаковым растворителем, при одинаковой температуре масса диспергированного вещества в этих системах выражается:
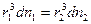
т.е. осмотическое давление обратно пропорционально кубу радиуса частиц и, следовательно, прямо пропорционально кубу степени дисперсности.
Значит небольшое изменение в размере частиц приведёт к значительному изменению осмотического давления.
🌟 Видео
ФОТОЭФФЕКТ И УРАВНЕНИЕ ЭЙНШТЕЙНА НА ПРИМЕРЕ ТЮРЬМЫСкачать

Уравнения математической физики. Уравнение теплопроводности (диффузии).Скачать

Закон диффузии ФикаСкачать

законы Столетова Уравнение Эйнштейна для внешнего фотоэффектаСкачать

Лекция 37 Связь коэффициента диффузии с предельной электропроводностьюСкачать

Лекция 26 Как изменяется скорость диффузии с расстояниемСкачать

Просто о сложном - ДиффузияСкачать

Лекция 29 Задача Коттрелла Cлучай неравных коэффициентов диффузииСкачать

Урок 12 (осн). Диффузия. Броуновское движениеСкачать

Теория относительности для чайников (часть 1)Скачать

Почему E=mc²?Скачать

Физика. ЕГЭ. Фотоэффект теория. Уравнение Эйнштейна.Скачать

Лекция 26 Диффузия и миграцияСкачать

Как Эйнштейн доказал Бога!!!Скачать

Урок 435. Теория фотоэффекта. ФотоэлементыСкачать

Дифференциальное уравнение Эйлера. Основное уравнение гидростатикиСкачать

Теория относительности Эйнштейна - о чём она? Простое объяснениеСкачать

8.5 Теория фотоэффектаСкачать