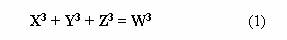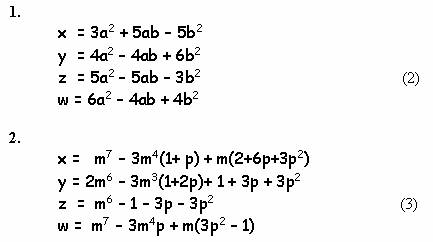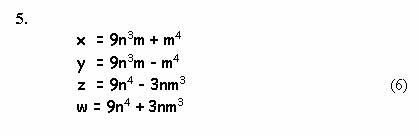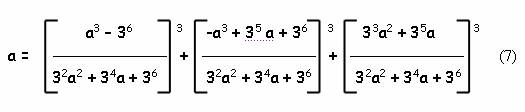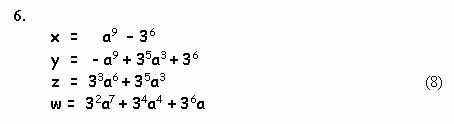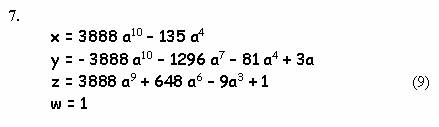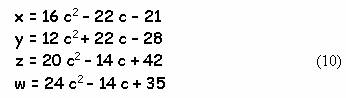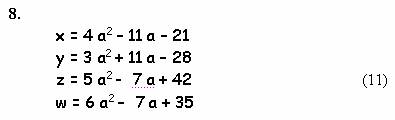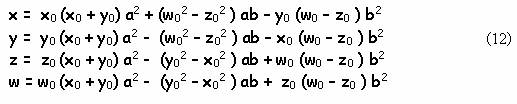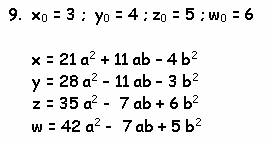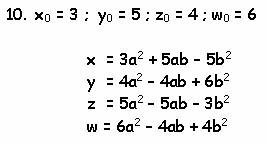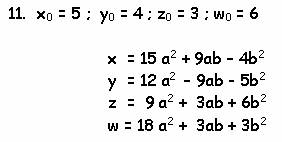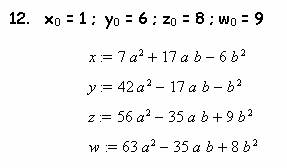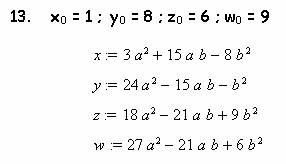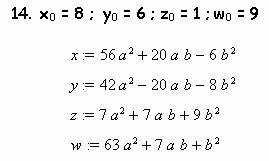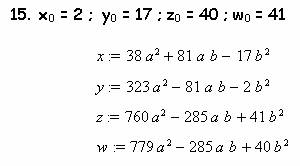Уравнение эйлера задача о четырех кубах (3 видео)

Содержание

Задача о четырех кубах. Часть 2
Уравнение эйлера задача о четырех кубах
Четыре куба.
Ответ
Решение задачи
О задаче
Скачать задачу
Оставить комментарий
Решите задачу
Занимательные задачи
📹 Видео

Видео:Задача о четырех кубах (4 kuba)Скачать

Задача о четырех кубах. Часть 2

УРАВНЕНИЕ ЭЙЛЕРА.
РЕШЕНИЕ ЭЙЛЕРА И БИНЕ

В данной работе речь пойдет об уравнении в целых числах, которое предложил более двух веков назад Леонард Эйлер (Рис.1). Полюбуйтесь им на рисунке Рис.2.
Леонард Эйлер (1707—1783 гг.) — математик, механик, физик и астроном, ученый необычайной широты интересов, автор свыше 800 работ по математическому анализу, дифференциальной геометрии, теории чисел, приближенным вычислениям, небесной механике, математической физике, оптике, баллистике, кораблестроению, теории музыки и др., оказавших значительное влияние на развитие науки. По происхождению швейцарец.
В 1726 г. был приглашен работать в Петербург, в 1727 г. переехал жить в Россию, в 1731—1741 и начиная с 1766 гг. был академиком Петербургской академии наук. В 1741—1766 гг. работал в Берлине, оставаясь почетным членом Петербургской Академии наук.
Он считал, что математика была и будет самой удивительной наукой, рожденной в головах многих выдающихся личностей. Она возникла и совершенствовалась в соответствии с нуждами практики, но оказалась настолько цельной и гармоничной, что сама явилась объектом тщательных исследований. Величайшие умы человечества, иногда по крупицам, а иногда и гейзером идей, открывали все новые и новые грани теории чисел, статистического анализа, изучения функций, дифференциального и интегрального исчислений, рядов, геометрии, тригонометрии, графов, топологии и т.д. и т.п. Основной целью математики чаще всего было нахождение области допустимых решений нужной задачи. Когда та или иная сложная проблема вдруг стопорилась, приходилось искать иные подходы, методы и даже создавать новые направления, которые позволяли преодолевать пробелы в математических знаниях. Так происходил прогресс науки о порядке.
Эти мысли гения математики актуальны и сегодня. Наиболее ярким примером сказанному служит, конечно же, Великая Теорема Ферма. Потребовалось целых 358 лет, чтобы ее безошибочно доказать!
Задача о четырех кубах тоже оказалась непростой. Но если в ВТФ требовалось доказать полное отсутствие решений, то в нашем случае, наоборот, нужно было найти систему выражений для x, y, z ,w которая давала бы все примитивные четверки Эйлера. Четверка Эйлера (x,y,z,w) называется примитивной, если она не может быть получена из какой-то другой четверки Эйлера, то есть x, y, z, w являются взаимно простыми числами.
Леонард Эйлер сам приложил немало усилий, чтобы найти формулы, генерирующие все примитивные четверки целых чисел
Проблема эта чисто алгебраическая и совсем непростая. Вспоминаю такой эпизод в моей жизни. Еще в школе прочитал решение Пифагора, при помощи которого можно находить все примитивные тройки чисел в задаче о трех квадратах. Года через три мне понадобились эти формулы, но я их совершенно забыл, а учебников под рукой не оказалось. Оставалось только самому вывести знаменитые соотношения. И что же? Промучился два часа, но так и не удалось повторить подвиг Пифагора. И это с квадратами! С кубами же такая задача на порядок сложней. Даже Эйлеру оказалось по силам вывести лишь зависимости, дающие хотя бесконечную, но далеко не полную серию x, y, z ,w (смотрите Рис.3). Проверим эффективность работы данных формул. Простая программа на языке Yabasic :

open #1,»340.txt»,»r»
open #2,»EULER2.txt»,»w»
dim x(10)
n=8:n0=4:s1=0.00001
rem Считываем примитивные четверки Эйлера
for v=1 to 340
input #1 r,x0,y0,z0,w0
k=0
for a=-n to n
for b=-n to n
x(1)=abs(1-(a-3*b)*(a^2+3*b^2))
x(2)=abs(-1+(a+3*b)*(a^2+3*b^2))
x(3)=abs(-a-3*b+(a^2+3*b^2)^2)
x(4)=abs(-a+3*b+(a^2+3*b^2)^2)
rem Распределяем массив чисел по возрастанию
for j=1 to n0-1
for i=1 to n0-j
if x(i)>x(i+1) then
t=x(i):x(i)=x(i+1):x(i+1)=t
fi
next i
next j
x=x(1):y=x(2):z=x(3):w=x(4)
rem Исключаем тривиальные и нелинейные варианты
if abs(x)abs(y) then
if abs(x)abs(z) then
if abs(x)abs(w) then
if abs(y)abs(z) then
if abs(y)abs(w) then
if abs(z)abs(w) then
if abs(x/x0-y/y0) «;
print #2, s,x0,y0,z0,w0;:print #2, » -> «;
print a,b:print #2, a,b:k=1:fi
fi:fi:fi:fi:fi:fi:fi:fi:fi
next b
next a
next v

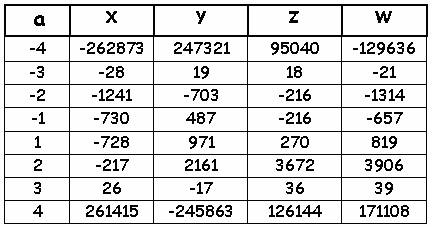
позволила установить, что из 340 известных числовых решений задачи о четырех кубах система Эйлера выявляет всего 25 решений, то есть меньше 10%.

Почти через сто лет такой же результат получил Бине (Рис.4).
Жак Филлип Мари Бине — французский математик и астроном, родился в Ренне 2 февраля 1786 г., умер в Париже 12 мая 1856 г. Окончив Политехническую школу, он был назначен в ней профессором механики и впоследствии главным инспектором. В 1823 г. Бине занял кафедру астрономии в College de France после Деламбра. В 1843 г. он был избран членом Академии наук на место Лакруа. Бине принял участие в новом издании «Mecanique analytique» Лагранжа. Напечатал массу статей по механике, чистой и прикладной математике и астрономии. Бине одним из первых пришёл к идеям матричной алгебры и первым опубликовал в 1812 году правило умножения матриц. С его именем связана формула Бине для чисел Фибоначчи, хотя эту формулу столетием ранее получил Абрахам де Муавр. Независимо от Эйлера нашел частное решение задачи о четырех кубах (формулы Эйлера и Бине). Бине принадлежит также ряд важных теорем в механике вращающихся тел.

Видео:06. Формула ЭйлераСкачать

Уравнение эйлера задача о четырех кубах

История математики оставила нам поразительно красивые проблемы, среди которых есть и нерешенные до сих пор. Об одной из задач, известной как задача о четырех кубах, пойдет речь в данной статье. Почему-то именно диофантову формулу, предложенную впервые Эйлером, крайне скудно освещают современные популярные труды. Отрывочные сведения удалось найти лишь в Интернете, в работе Г.Харди «Двенадцать лекций о Рамануджане» и справочных пособиях по математике.

Леонард Эйлер (1707—1783 гг.) — математик, механик, физик и астроном, ученый необычайной широты интересов, автор свыше 800 работ по математическому анализу, дифференциальной геометрии, теории чисел, приближенным вычислениям, небесной механике, математической физике, оптике, баллистике, кораблестроению, теории музыки и др., оказавших значительное влияние на развитие науки. По происхождению швейцарец.

В 1726 г. был приглашен работать в Петербург, в 1727 г. переехал жить в Россию, в 1731—1741 и начиная с 1766 гг. был академиком Петербургской академии наук. В 1741—1766 гг. работал в Берлине, оставаясь почетным членом Петербургской Академии наук.

Математика, вне всякого сомнения, была и будет самой удивительной наукой, рожденной в головах многих выдающихся личностей. Она возникла и совершенствовалась в соответствии с нуждами практики, но оказалась настолько цельной и гармоничной, что сама явилась объектом тщательных исследований. Величайшие умы человечества, иногда по крупицам, а иногда и гейзером идей, открывали все новые и новые грани теории чисел, статистического анализа, изучения функций, дифференциального и интегрального исчислений, рядов, геометрии, тригонометрии, графов, топологии и т.д. и т.п. Основной целью математики чаще всего было нахождение области допустимых решений нужной задачи. Когда та или иная сложная проблема вдруг стопорилась, приходилось искать иные подходы, методы и даже создавать новые направления, которые позволяли преодолевать пробелы в математических знаниях. Так происходил прогресс науки о порядке.. Наиболее ярким примером сказанному служит, конечно же, Великая Теорема Ферма. Потребовалось целых 358 лет, чтобы ее безошибочно доказать!

В уравнении Эйлера

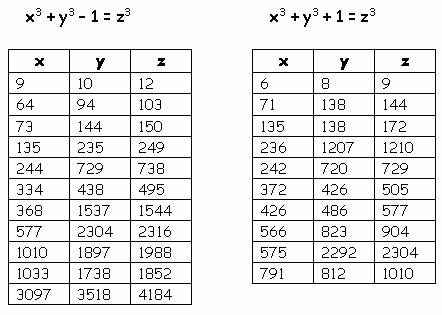
значения X , Y , Z и W целочисленные. Данная математическая головоломка известна еще как задача о четырех кубах. Требуется найти все ее решения. Отдельные арифметические результаты были известны еще Диофанту – древнегреческому математику, занимавшемуся вопросами анализа уравнений с целыми коэффициентами. Сколь угодно большое количество четверок чисел можно найти при помощи элементарной программы на компьютере. Вот некоторые варианты:

Но общей формулы, позволяющей находить данные значения, выявить до сих пор не удалось.

Суммируем все, что известно

Вот два варианта, найденные великим индийским математиком Рамануджаном (1887 – 1920 гг.):

В 1956 году математик Л. Мордел (см.ссылку http://neves.suncloud.ru/task/fermat25.htm) получил следующие весьма любопытные двухпараметрические зависимости:

Выведенное мною объединение последних вариантов (4) и (5) дает еще одно решение:

Математиками давно было доказано, что любое рациональное число можно представить в виде суммы трёх кубов рациональных чисел. Наглядно это демонстрирует потрясающая по красоте формула, полученная еще в 1825 году:

где а – любое действительное число. Отталкиваясь от данного соотношения, мне довольно легко удалось найти громоздкое однопараметрическое решение уравнения Эйлера:

Вычислим для интереса несколько значений коэффициентов уравнения :

И 1955 году математик Д.Лемер обнаружил еще один необычный вариант:

Простейшие численные решения такие:

Ссылка http://rusnauka.narod.ru/lib/matem/labkovsky/ привела меня к интересной работе «Элементарные уравнения Диофанта», написанной преподавателем математики Лабковским Виленом Борисовичем. В ней приведено довольно простое решение уравнения (1):

Совокупность (10) , как ни странно, допускает существенное упрощение. В самом деле, если произвести замену а = 0,5 c , то :

Мы кратко обрисовали состояние дел по интересующему нас вопросу. Можно было бы попытаться найти еще больше формул, но, как мне кажется, и восьми примеров вполне достаточно, чтобы показать всю сложность проблемы. Складывается такое ощущение, будто представленные алгебраические связи выведены простым интуитивным подбором. Часть решений получаются при изменении одного параметра (примеры №№ 6 – 8), а часть – при изменении двух параметров (примеры №№ 1 – 5).

Моя цель – дать наиболее общие связи для четырёх параметров в уравнении Эйлера, из которых, как частные случаи, могли бы отпочковываться четверки целых чисел.

Методом проб и ошибок, анализом огромного количества конкретных вычислений и вовлечением в этот процесс таинственной интуиции, мне удалось сформировать до сих пор непонятные, но чудотворные соотношения:

Если в (12) подставлять в качестве начальные значений параметров любые известные целые числа, удовлетворяющие уравнению (1), то, как из рога изобилия, будут находиться другие решения. Подтвердим сказанное на нескольких примерах. Примем в качестве начальных параметров такие:

Параметры можно перетасовывать, получая новые связи:

А это как раз и есть система (2), полученная Рамануджаном! Просто потрясающее открытие! Знал ли великий индийский математик о существовании решения (12) ?

Подобные формулы можно без особых усилий составить из других вариантов чисел x ₀ ; y ₀ ; z ₀ ; w ₀ . Каждая такая система, тем не менее, — на вес золота, поскольку открывает новое поле конкретных решений.

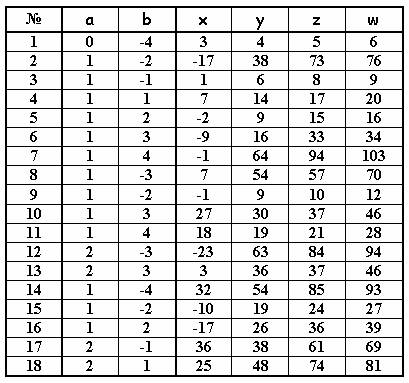
Можно до бесконечности продолжать генерацию все новых и новых систем. Мною была проделана такая интересная работа. Я задал начальные значения x ₀ = 3 , y ₀ = 4 , z ₀ = 5 , w ₀ = 6 и по специально написанной программе на Бейсике нашел 18 различных вариантов при условии, что w ≤ 103 :

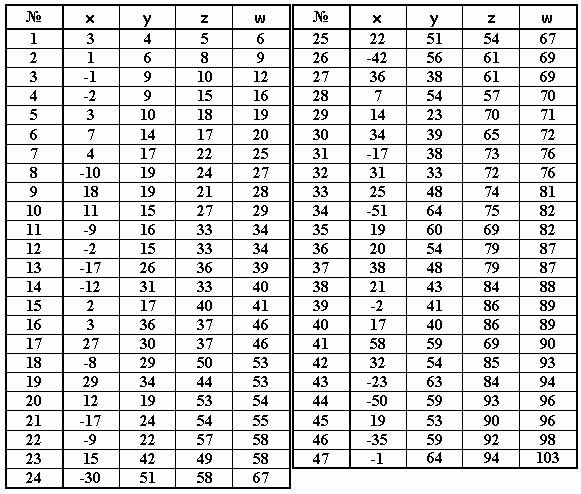
Подставляя эти данные опять в ту же программу, выявил еще 47 вариантов

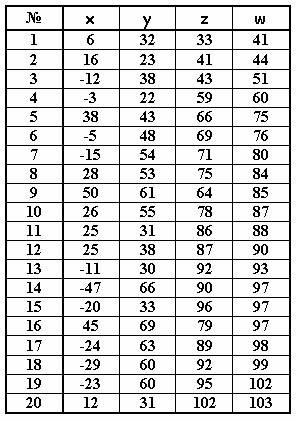
К сожалению, никак не проявили себя следующие 20 четверок чисел:

Как получить эти последние решения – совершенно неясно. Утешением может служить только то, что приблизительно 74% вариантов найдено по цепочке с помощью системы (12) опираясь только на начальные параметры x ₀ = 3 ; y ₀ = 4 ; z ₀ = 5 ; w ₀ = 6 . А это совсем немало.

Видео:✓ Формула Эйлера для графов и многогранников за 8 минут | Ботай со мной #103 | Борис ТрушинСкачать

Четыре куба.

Из одного и того же материала изготовлено четыре сплошных куба различной высоты, а именно в 6 см, 8 см, 10 см и 12 см. надо разместить их на весах так, что бы чашки были в равновесии.

Видео:#161. САМАЯ КРАСИВАЯ ФОРМУЛА В МАТЕМАТИКЕ — ФОРМУЛА ЭЙЛЕРА: e^(iπ)+1=0Скачать

Ответ

12 см на одну и 6, 8, 10 см. на другую.

Видео:Дифференциальное уравнение. Формула ЭйлераСкачать

Решение задачи

Масса кубов пропорциональна их объему или кубу одного из линейных размеров, например, высоты. Получаем, для куба со стороной 6 см., объем равен 216 см 3 , 8 см. — 512 см 3 , 10 см. — 1000 см 3 , 12 см. — 1728 см 3 . Таким образом, привести весы в равновесие можно если разместить кубы следующим образом: на одну чашу покласть куб со стороной 12 см. и объемом 1728 см 3 , а на другую — три куба со сторонами 6, 8 и 10 см. и суммарным объемом 216+512+1000=1728 см 3 .

Видео:Основы вариационного исчисления | уравнение Эйлера Лагранжа | конкретные примеры | 4Скачать

О задаче

Категория: Геометрические задачи, Задачи на взвешивание, Задачи с подвохом,
Степень сложности: средняя.
Ключевые слова: 4, 6, 8, 10, 12, весы, куб,
Источник: Живая математика, Наука на досуге,

Видео:11 класс, 49 урок, Задача ЭйлераСкачать

Скачать задачу

Вы можете скачать изображение с текстом задачи, поделиться им с друзьями в социальных сетях либо использовать в презентациях. Для скачивания, нажмите на картинке.