Простейшую вариационную задачу можно обобщить на случай, когда подынтегральная функция содержит производные высших порядков и функционал имеет вид

Здесь функция F предлагает (n+2) раза дифференцируемой по всем аргументам, а граничные условия заданы в форме
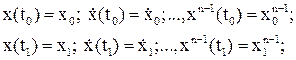
т.е. в граничных точках заданы значения не только функции, но и ее производных до порядка (n-1) включительно (всего 2n условий).
Решение задачи J = min ищется в классе C2n[t0,t1] гладких 2n раз дифференцируемых функций. Методика получения необходимого условия минимума функционала остается прежней: находится первая вариация критерия и приравнивается к нулю, что после преобразований приводит к уравнению
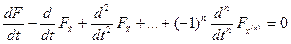
которые называются уравнением Эйлера-Пуассона и представляет в общем случае нелинейное дифференциальное уравнение 2n-порядка.
Его решение x(t,c1,c2,…,c2n) содержит 2n постоянных интегрирования. Последние находятся на основании такого же количества граничных условий (2).
Дадим вывод уравнения (3), ограничившись для простоты выкладок случаем, когда функционал зависит от производной не старше второго порядка:

Предположим, что экстремум достигается на функции x(t), и прибавим к ней вариацию 

Определим вариацию функционала



Преобразуем теперь выражение (5), пользуясь формулой интегрирования по частям, причем третий член вариации будем интегрировать по частям дважды:



Вследствие условий на концах участка все неинтегральные члены обращаются в нуль, и, следовательно, на основе (5) — (7) получаем
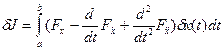
Поскольку необходимым условием экстремума является равенство нулю первой вариации функционала, а вариация 

В этом случае имеет место следующий аналог условия Лагранжа, позволяющий отличить максимум от минимума функционала (1): если функция x(t) доставляет минимум (максимум) функционалу, необходимо, чтобы 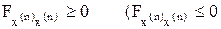
Пример. Применим теорему Лежандра к функционалу
Следовательно, функционал достигает минимума на функции x(t) = t 2 , которую мы определили ранее.
Проверим это. Для чего подставим экстремаль в функционал и вычислим его значение



Для сравнения вычислим значения функционала, например, на прямой линии, соединяющей те же точки (см. предыдущий рис.) – x(t) = t:

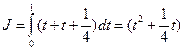

Таким образом, мы убедились, что на экстремали x(t) = t 2 значения функционала меньше, чем на кривой x(t) = t: 

6. Задачи на условный экстремум: метод множителей Лагранжа.
Решение многих технических вопросов приводит к таким вариационным задачам, в которых функции, доставляющие экстремум должны, кроме того, удовлетворять некоторым дополнительным условиям. Так, например, в задаче о кратчайшей морской трассе на поверхности земного шара нужно найти минимум функционала – длины кривой

при условии, что эта кривая лежит на поверхности земного шара, т.е. удовлетворяет уравнению сферы 
Экстремум функционала, определяемый при таком дополнительном условии называется условным экстремумом.
Наиболее простой в методическом плане способ решения указанной задачи на условный экстремум состоит в следующем. Из уравнения (2) выражаем функцию z(x) через функцию y(x)
и дифференцируем ее по х:

Подставляем функцию (3) в функционал (1)


Таким образом исходная задача на условный экстремум (1), (2) сведена к стандартной задаче на поиск экстремума функционала (4).
Однако необходимо подчеркнуть, что указанная процедура исключения неизвестных приводит часто к сложным вычислениям, а во многих случаях не может быть выполнена точно аналитически. В связи с этим Лагранжем был предложен другой достаточно простой метод решения – метод неопределенных множителей (множителей Лагранжа).
Сформулируем в общем виде задачу на условный экстремум.
Пусть задан функционал
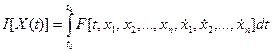
при наличии условий 
Функции 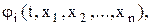
Теорема. Если X(t) – экстремаль функционала (4), удовлетворяющая условиям (5),(6), то она удовлетворяет уравнениям Эйлера, составленным для функционала

где 
В соответствии с данной теоремой, экстремали функционала (4) и функции 


так называемая функция Лагранжа.
Таким образом экстремаль задачи (4) — (6) определяется обычными методами поисками экстремалей функционала

Докажем справедливость теоремы на примере задачи при n=2, m=1:



Записываем функцию Лагранжа 

Для определения трех функций x(t), y(t), 




Для доказательства теоремы получим соотношения (12) с использованием вариационных методов. Предположим, что экстремум функционала (10) доставляется функциями x(t) и y(t); добавим к ним вариации 

Отметим, что поскольку определяются не достаточные, а только необходимые условия экстремума, то вариации 
Вариация функционала (10) будет равна

Однако вариации 

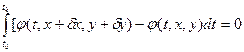
Используя понятие дифференциала функции многих переменных и теорему о значении определенного интеграла, соотношение (14) преобразуем к виду

Подставляя равенство (15) в выражение для вариации (13), получаем

откуда вследствие 

Обозначая правую и левую часть равенства (16) через 
7. Вариационные изопериметрические задачи. Особенности их решения.
Как частный случай задачи Лагранжа можно рассматривать и представляющую самостоятельный интерес изопериметрическую задачу, когда условия которым подчинена искомая функция, заданы в интегральной форме. Например, простейшая задача формулируется следующим образом: определить экстремум функционала

при условии, что другой функционал
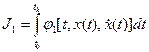
сохраняет заданное значение С, а экстремаль проходит через точки: x(t0)=x0; x(tk)=xk. Название изопериметрических такого рода задачи получили по названию одной из них: среди всех кривых равной длины (одинакового периметра) найти ту, которая ограничивает наибольшую площадь. Эта задача была известна еще древним грекам под названием «задача Дидоны». По преданию, легендарная основательница Карфагена царица Дидона покупала у туземцев землю, на которой должен быть основан город. Ей согласились продать лишь участок, который можно охватить бычьей шкурой. Тогда Дидона разрезала шкуру на тонкие ремни и расположила их так, чтобы охватить наибольшую площадь. Если пользоваться современными математическими понятиями, Дидона решила именно изопериметрическую задачу, выбирая функцию y(x), доставляющую максимум интегралу

(площади, охваченной ремнем), при заданном значении интеграла

Изопериметрическую задачу легко свести к общей задаче Лагранжа. Действительно, обозначив

(интеграл с переменным верхним пределом), получим

и приходим к следующей задаче Лагранжа: найти функции x(t), 

Согласно теореме, для решения этой задачи следует составить уравнение Эйлера для вспомогательной функции 


Из второго уравнения (29) следует, что 


Таким образом, получаем следующее мнемоническое правило: для того чтобы найти функцию x(t), доставляющую экстремум интегралу (22) при условии, что интеграл (23) сохраняет заданное значение, следует составить одно уравнение Эйлера для промежуточной функции

В решение уравнения Эйлера будут входить три произвольные постоянные – две постоянные интегрирования и постоянная 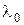
Применяя это правило к задаче Дидоны можно установить, что ее решение является окружностью с радиусом 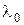
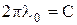

8. Функционалы, зависимые от многих функций: уравнения Эйлера, условие Лежандра.
Одним из обобщений простейшей вариационной задачи является задача отыскания экстремума функционала, зависящего от n функций 
при заданных граничных значениях для всех функций

Требуется в классе функций C1[t0,t1] найти функции xi(t), i=1,2,…,n, проходящие через граничные точки (10) и доставляющие минимум функционалу (9).
Для получения необходимых условий экстремума рассматриваемого функционала будем варьировать лишь одну из функций xi(t), i=1,2,…n, оставляя все остальные функции неизменными. При этом функционал 



Так как это рассуждение применимо к любой функции xj, j=1,2…,n ,то получаем систему дифференциальных уравнений Эйлера

которая определяет совокупность необходимых условий экстремума вариационной задачи (9), (10).
Экстремали, соответствующие системе (11), содержат 2n постоянных интегрирования, находящихся из заданных граничных условий (10).
В современной литературе по теории оптимального управления полученный результат часто записывают в матричной форме. Введем в рассмотрение вектор 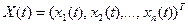
Используя понятие производной скалярной функции 
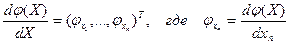
условия (11) можно записать в компактной матричной форме 
(полный аналог скалярного уравнения Эйлера).
Используя матричные операции легко записать условия Лежандра для функционала (9). С этой целью введем в рассмотрение матрицу




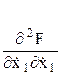




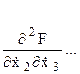





которая является аналогом скалярного выражения 
Для достижения на некоторой совокупности экстремалей минимума функционала (9) необходимо, чтобы все угловые миноры этой матрицы были неотрицательны, т.е.


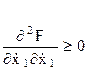




где 
Для достижения максимума J неравенства (14) должны иметь противоположный знак.
Функционал (9) может содержать производные высших порядков. В этом случае система уравнений будет состоять из уравнений Эйлера-Пуассона.
9. Применение классического вариационного исчисления к задаче оптимального управления, двухточечная краевая задача.
10. Применение классического вариационного исчисления к задаче оптимального управления, уравнения Эйлера — Лагранжа в канонической форме.
Вспомним теперь формулировку задачи оптимального управления с закрепленными концами. Объект управления описывается уравнениями

Требуется найти вектор управляющих воздействий u(t) и соответствующую фазовую траекторию x(t) при условии, что X(t0) = X0, X(tk) = Xk и функционал
принимает экстремальное значение.
Очевидно, что сформулированная задача по существу является вариационной задачей и отличается от обычной вариационной задачи на условный экстремум только тем, что в нее входят два вида функций: функция X(t), характеризующая состояние системы, и функция управления U(t).Это отличие не принципиально и легко показать, что задача оптимального управления, удовлетворяющая основным положениям классического вариационного исчисления (отсутствие ограничений на фазовые координаты и управляющие воздействия, непрерывность и дифференцируемость управляющих воздействий), является общей задачей Лагранжа. Действительно, интеграл (9) можно рассматривать как функционал, зависящий от n+m функций x1,…,xn, u1,…,un.
Эти функции связаны дифференциальными уравнениями объекта (8), которые можно записать в виде уравнений связи
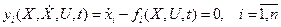
Следовательно, для решения задачи оптимального управления, которая удовлетворяет основным положениям классического вариационного исчисления, можно использовать метод неопределенных множителей Лагранжа и записать необходимое условие экстремума функционала (9) при наличии ограничения (10) в виде уравнения Эйлера – Лагранжа. Согласно методу неопределенных множителей введем вспомогательный функционал


есть функция Лагранжа. Тогда уравнение Эйлера-Лагранжа будут иметь вид

В дальнейшем будем использовать, так называемую каноническую форму записи уравнений Эйлера-Лагранжа. Такая форма записи уравнения Эйлера-Лагранжа имеется в вариационном исчислении мы рассмотрим ее применительно к задачам оптимального управления.
Введем функцию, называемую гамильтонианом (функция Гамильтона).

(l0=-1) и сравним ее с функцией Лагранжа (12). Выразим вспомогательную функцию L через гамильтониан H:

(т.е. к функции H добавлено слагаемое, которое отличает ее от функции L).
Запишем необходимое условие экстремума (уравнения Эйлера-Лагранжа) с использованием функции H. Для частных производных, которые входят в уравнения Эйлера-Лагранжа (13) согласно (15) имеем


Подставим найденные выражения в (13), получим уравнения Эйлера-Лагранжа в канонической форме:
Здесь уравнения (17а) являются уравнениями объекта (8). Уравнения (17б), записанные относительно вспомогательных переменных 
Уравнения (17в) являются алгебраическими. Действительно
Заметим, что значения функции, удовлетворяющие условию в виде (17в), называются стационарными значениями функции, а точки пространства аргументов, в которых эти условия выполняются — стационарными точками (стационарными называются точки, в которых производная функции равна нулю). Следовательно, оптимальное управление есть стационарная точка функции Гамильтона.
Уравнения (19) позволяют определить управление в виде функции



Общее решение такой системы, как известно, зависит от 2n параметров (начальных условий) поскольку управление найдено как функция (X и l). В задаче с закрепленными концами n параметров задано на левом конце фазовой траектории (X(t0)=X0), и n параметров на правом конце (X(tk)=Xk). Такая задача называется краевой.
Таким образом решение задачи оптимального управления оказалось сведенным к решению краевой задачи для систем дифференциальных уравнений. Отметим, что в силу только необходимости уравнений Эйлера-Лагранжа решения системы (17) не обязательно дают оптимальное управление, но только решение системы (17) могут претендовать на роль оптимального управления. С помощью уравнений Эйлера-Лагранжа обычно удается найти оптимальное управление и оптимальную траекторию системы, поскольку существование и характер экстремума функционала в конкретной задаче оптимального управления, как правило, известно заранее.
Пример. Определим из условия минимума функционала

оптимальное управление U(t) для объекта, описываемого уравнениями
составим функцию Гамильтона

Уравнение Эйлера-Лагранжа имеет вид

Из последнего уравнения имеем 
Исключим из оставшихся двух уравнений l. Для чего подставим уравнение (26) в первое уравнение (25)

откуда
Затем продифференцируем
После чего подставим 
Окончательно имеем уравнение относительно x(t):

Решением этого уравнения является функция

Постоянные С1 и С2 определяются из граничных условий. Так как x(¥)=0, то

и для выполнения (29) необходимо положить С1=0.
При t=0 имеем x(0)=x0, тогда

и для выполнения равенства (30) должно быть С2 = x0, следовательно

Используя уравнение (23) – уравнение объекта, найдем

Управление (32) найдено как функция времени и начальных условий – это так называемое программное управление.
В данном примере легко найти и управление в форме обратной связи. Из сравнений выражений (31) и (32) следует

Видео:06. Формула ЭйлераСкачать

Различные обобщения уравнения Эйлера. Уравнение Пуассона-Эйлера и Остроградского.
Читайте также:
|









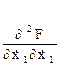









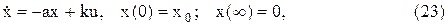





 ,
,  ,
,  ,
,  (2)
(2)
 , которые удовлетворяют краевым условиям (2). Тогда, очевидно, приращения δy(x) должны удовлетворять краевым условиям
, которые удовлетворяют краевым условиям (2). Тогда, очевидно, приращения δy(x) должны удовлетворять краевым условиям ,
,  (4)
(4)
 , (6)
, (6)
 ,
,  имеет вид
имеет вид

 –известна.
–известна.
 — множество непрерывно дифференцируемых функций в замыкании области Ω.
— множество непрерывно дифференцируемых функций в замыкании области Ω. (x, y) — решение вариационной задачи, а z(x, y) — любая другая функция из D(J), то
(x, y) — решение вариационной задачи, а z(x, y) — любая другая функция из D(J), то
 (2)
(2) ,
, 

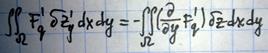
 (3)
(3) ,
,  (на Γ= ∂Ω)
(на Γ= ∂Ω)