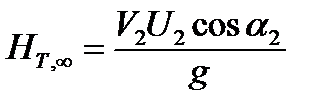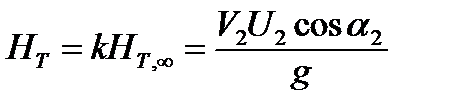Уравнение эйлера для центробежного насоса (2 видео)

Содержание

Теоретический напор насоса, формула Эйлера
Уравнение Эйлера
Уравнение эйлера для центробежного насоса
📺 Видео

Видео:Теоретический напор центробежного насосаСкачать

Теоретический напор насоса, формула Эйлера

Во вращающемся рабочем колесе на частицы жидкости действует центробежная сила:

F= m ω 2 R = ρ∙V∙ ω 2 R

Где Fц- центробежная сила

V – объем частиц

ω- угловая скорость

R- радиус рабочего колеса

В результате этого в центре колеса падает давление, создается разрежение, а на периферии колеса давление повышается, тем самым создается напор.

Движение жидкости в межлопаточных каналах вращающегося колеса можно рассматривать как результат сложения двух движений: переносного (вращение колеса) и относительного (движение относительно колеса).

Поэтому вектор абсолютной скоростижидкости в колесе V может находиться как сумма векторов окружной скорости U и относительной скорости W.

При этом относительная скоростьWнаправлена по касательной к лопатке, а окружнаяU — по касательной к соответствующей окружности.

Параллелограмм скоростей можно построить для любой точки на лопатке.

Если все величины, относящиеся к входу на лопатку, отмечать индексом 1, а величины, относящиеся к выходу, — индексом 2, а угол между векторами скоростей окружной и абсолютной обозначим через a, а между касательной к лопатке и касательной к окружности колеса, проведенной в сторону, обратную вращению, — через b ,то можно получить формулу для расчета теоретического напора (формула Эйлера)

(12)

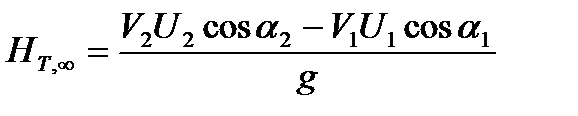
Для вывода основного уравнения теории центробежного насоса принимают следующие два допущения:

1. Насос имеет бесконечно большое число одинаковых лопаток (z=¥), а толщина этих лопаток равна нулю (b=0). Это допущение означает, что мы предполагаем в межлопаточных каналах колеса такое струйное течение, при котором форма всех струек в относительном движении совершенно одинакова и точно соответствует форме лопаток, а скорости зависят только от радиуса и не меняются на окружности данного радиуса. Это положение может иметь место лишь в том случае, когда каждая элементарная струйка направляется своей лопаткой.

2. Коэффициент полезного действия насоса равен единице (h=1), т.е. в насосе отсутствуют все виды потерь энергии и, следовательно, вся мощность, которая затрачивается на вращение колеса, целиком передается жидкости Такая работа насоса возможна лишь при перекачке идеальной жидкости, при отсутствии зазоров в насосе, а также при отсутствии механического трения в сальниках и подшипниках

Такой насос, у которого z=¥ и h=1, называетсяидеальным центробежным насосом.

Обычно жидкость подходит к рабочему колесу насоса без предварительной закрутки, а войдя в колесо, вступает в межлопаточные каналы, двигаясь радиально Это значит, что вектор V₁ направлен по радиусу, а угол a₁=90°. Следовательно, второй член в уравнении делается равным нулю и уравнение принимает вид

Эта форма уравнения Эйлера более употребительна.

Реальное колесо центробежного насоса имеет Z=4-8, a₂ = 5 — 10 0 , b₂ = 20 — 40 0 .

В этом случае поток в относительном движении уже не следует строго по направлению лопаток, что проводит к снижению теоретического напора Н_Т по сравнению с Н_Т∞..

где: К — поправка на коническое число лопаток,

Коэффициент К = 0,6 — 0,8 и зависит от кинематики и конструкции колеса.

Формула показывает, что для получения с помощью центробежного насоса больших напоров нужно иметь,

во-первых, большую окружную скорость вращения колеса и,

во-вторых, достаточную закрутка потока жидкости колесом.

Первое достигается соответствующими значениями числа оборотов и диаметра колеса, а второе — достаточным числом лопаток, их размером и формой.

Видео:Как работает центробежный насос? Основные типы конструкций центробежных насосовСкачать

Уравнение Эйлера

Жидкость, перекачиваемая под действием центробежной силы насосом, при прохождении через межлопаточные пространства (каналы) рабочего колеса приобретает как потенциальную, так и кинетическую энергию.

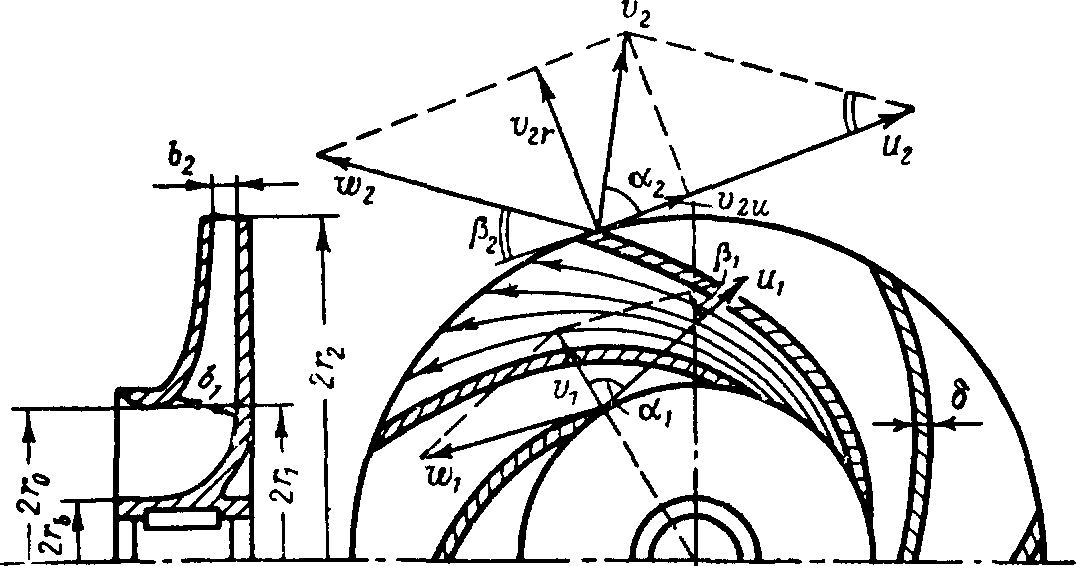
На рис. 2.25 изображена схема изменения направления скоростей на рабочем колесе при входе жидкости на рабочую лопатку и выходе с нее. Энергия в потоке жидкости увеличивается в результате силового воздействия лопаток колеса на жидкость и соответствующего расхода энергии двигателя, приводящего насос в действие. Напор, развиваемый насосом, может характеризовать удельную энергию, т. е. энергию, приобретенную единицей массы жидкости.

Рис. 2.25. Схема изменения направления скоростей на рабочем колесе насоса

Эйлер вывел уравнение для определения теоретического напора при следующих допущениях: а) перекачиваемая жидкость является идеальной (при ее протекании через проточную часть насоса исключаются гидравлические сопротивления); б) рассматриваемый насос имеет бесконечно большое число лопаток, благодаря чему все частицы жидкости движутся внутри колеса по одинаковым траекториям, имеющим очертания лопаток.

Бесконечное число лопаток дает бесконечно узкий канал для прохода жидкости и обеспечивает ламинарный характер течения жидкости, что упрощает построение векторной диаграммы на выходе. Допустим, что за 1 с через колесо протекает масса жидкости т. При входе в лопаточное колесо частица жидкости получает окружную скорость направленную по касательной к окружности входных кромок и равную u1 = 0,5ωD1, где ω — угловая скорость колеса насоса (по часовой стрелке); D1 — диаметр внутренней окружности колеса. Кроме того, жидкость получает относительную скорость ω1 которая направлена по касательной к контуру лопатки от положения входа.

Абсолютная скорость с1 может быть найдена построением параллелограмма, сторонами которого являются векторы скорости u1 и ω1. После того как частица жидкости совершила путь вдоль лопаток колеса, при выходе она будет иметь окружную скорость u2, направленную по касательной к наружному контуру колеса, и относительную ω2, направленную по касательной к контуру лопатки. Построив параллелограмм, можно найти абсолютную скорость выхода с2. Напор Ht∞ (t — идеальная жидкость; ∞ — бесконечно большое число лопаток) определяется на основании закона, известного из теоретической механики, по которому приращение момента количества движения материальной системы относительно данной оси за некоторый промежуток времени равно моменту импульса всех внешних сил за тот же промежуток времени (например, за 1 с).

Количество движения массы жидкости при входе равно произведению массы на скорость F1 = mc1, а при выходе F2 = mс2. Момент количества движения массы жидкости при входе равен 0,5mc1D1 cos α1, момент количества движения массы жидкости при выходе 0,5mc2D2 cos α2, где α1, α2 — углы между направлениями абсолютной и окружной скоростей. Момент импульса внешних сил равен разности моментов количества движения М = 0,5 (mc2D2 cos α2 — mc1D1 cos α1). Для упрощения обе части уравнения умножим на угловую скорость и разделим на массу, а левую часть разделим и умножим на ускорение свободного падения:
Mωg/(mg) = 0,5 (ωc2D2 cos α2 — mc1D1 cos α1. (2.6)
Известно, что мощность равна произведению угловой скорости и момента импульса внешних сил: N = ωМ. Если мощность выразить через теоретический напор, то она равна N = mgHt∞, откуда
Ht∞ = N/(mg). (2.7)
Заменяя в уравнении (2.6) произведение Мω на N и помня, что u1 = 0,5ω1D1 и u2 = 0,5ω2D2, получаем N/(mg) = (c2u2 cos α2 —с1u1 cos α1)/g. С учетом равенства (2.7) теоретический напор определится из выражения Ht∞ = (c2u2 cos α2 — c1u1 cos α1)/g.

Полный теоретический напор равен сумме статического и динамического напоров: Ht∞ = Hст + Hдин. Это очевидно из другого уравнения Эйлера, полученного через уравнение Бернулли: Ht∞ = Hст + Hдин = (n2 — u1)/(2g) + (w1 — w2)/(2g) + (c2—c1)/(2g).

Так как проекция абсолютной скорости на направление окружной скорости u2 представляет собой тангенциальную составляющую абсолютной выходной скорости с2, то она вычисляется по выражению c2u = с2 cos a2. Ввиду того что у большинства центробежных насосов отсутствуют направляющие аппараты при входе жидкости на лопатки и во избежание больших гидравлических потерь от ударов жидкости о лопатки угол ах принято выбирать равным 90°. Но cos 90° = 0, следовательно, c1u1 cos а1 = = 0. Таким образом, получаем основное уравнение центробежного насоса, или уравнение Эйлера:
Ht∞ = u2c2 cos a2/g = u2c2u/g. (2.8)
Основные уравнения для получения теоретического напора Ht в центробежном насосе были получены при условии, что траектория каждой частицы жидкости, движущейся по рабочему колесу, совпадает с профилем лопатки. Это было бы возможно лишь в том случае, когда каждая элементарная струйка направлялась бы двумя бесконечно тонкими лопатками, которых потребовалось бы бесконечно большое число. В действительном насосе число лопаток ограничено и они имеют определенную толщину. Это приводит к искажению треугольников скоростей, пересечению струек жидкости и образованию различных завихрений. Затраты на эти потери энергия снижают создаваемый напор на величину коэффициента φ = 1/, где ψ — технологический коэффициент, который зависит от степени обработки проточной части и угла β2 между направлениями относительной и окружной скоростей, находится по соотношению ψ= (0,55÷0,65) + 0,6 sin β1 ≈ 0,8÷1,3; z = 6÷9 — число лопастей судового насоса.

Для получения действительного напора необходимо учитывать также потери на преодоление гидравлических сопротивлений в насосе. Тогда (2.8) может быть преобразована в формулу действительного напора Hд = Ht∞φηr=u2c2uφηr/g.

Видео:Теорема Эйлера о движении жидкостиСкачать

Уравнение эйлера для центробежного насоса

Элементарная струйная теория центробежных машин была создана в России JI. Эйлером. Формула JI. Эйлера (2.4) является основной теоретической схемой при расчетах центробежных машин. В соответствии с этой теорией движение жидкости в канале между лопастями центробежного колеса при достаточно большом их числе (откуда эта теория получила и другое название — теория бесконечного числа лопастей) и незначительной ширине колеса приближенно может рассматриваться как струйное. Из уравнения неразрывности может быть определена средняя относительная скорость и ее направление как касательное к средней линии тока. При бесконечно большом числе бесконечно тонких лопастей поток в области колеса становится осесимметричным (). Относительная скорость, которая определяется уравнением неразрывности уже для каждой точки области, оказывается направленной по касательной к поверхности лопастей в рассматриваемой области. Схема бес^ конечного числа лопастей создает элементарное представление о кинематика потока в области колеса. Она служит отправной схемой одноразмерной теории центробежного колеса, исследующей параметры гидромашин при максимальном к. п. д. Здесь элементом закручивания потока в проточных каналах гидромашины пренебрегают, считая этот поток струйным в подводящем патрубке,, колесе или отводящем патрубке или создавая условия струйности конструкцией насоса. Действительное же распределение относительных скоростей в канале колеса конечных размеров не может быть осесимметричным из-за силового, взаимодействия между лопастью и потоком. Давление с напорной стороны лопасти будет больше, чем со всасывающей. Скорости со всасывающей стороны лопасти должны быть больше, чем с напорной

Академик Г. Ф. Проскура в 1931 г. разработал вихревую теорию центробежных насосов, согласно которой поток во вращающейся круговой решетке, лопастей может с достаточной степенью точности рассматриваться как состоящий из двух потоков: одного, получаемого конформным преобразованием относительного потока в плоской неподвижной решетке в относительный поток в неподвижной круговой решетке; второго — обусловленного осевым вихрем (вихрем относительной скорости), т, е. в канале между лопастями рабочего колеса в относительном движении жидкости (скорости w) получим вращение жидкости в сторону, обратную вращению колеса ( 2.10).

вихревое движение жидкости при нулевой подаче (w — 0 и Q = 0). Вихревое относительное движение жидкости в канале между лопастями колеса обладает скоростями, совпадающими по направлению с основным потоком со всасывающей стороны лопасти, и скоростями, обратными по направлению основному потоку — с напорной стороны лопасти. Осевой вихрь переносного движения, накладываясь на основной поток, приводит к повышению относительных скоростей на всасывающей стороне и к понижению их на напорной, содействуя распределению скоростей в канале колеса, необходимых для работы лопасти. Следуя вихревой теории центробежных насосов Г. Ф. Проскуры, можно отметить, что при нулевой подаче основной расход напора идет на вихреобразование в межлопаточном канале (вихри замыкаются в межлопаточном канале). К. п. д. насоса равен нулю; по мере роста подачи, т. е. увеличения относительной скорости, вихри, накладываясь на основной поток, сносятся в напорную линию, частично преобразуясь в полезную энергию. При этом напор и, следовательно, к. п. д. машины растут. При оптимальной подаче преобладающим становится поступательное движение жидкости, и потеря напора уже растет из-за трения жидкости в каналах колеса, а при максимальной подаче это сопротивление трению потребляет весь напор, создаваемый насосом. Интенсивность вихреобразования остается постоянной на всех режимах подачи. Такое разложение потока на составляющие следует рассматривать как приближенное.

Предположение о бесконечно большом числе бесконечно тонких лопастей в применении к рабочему колесу центробежного насоса
Другой причиной уменьшения напора по сравнению с его значением, подсчитанным по уравнению Эйлера, являются гидравлические потери.

образом, это воздействие на про. текающую жидкость сил давления со. стороны лопастей рабочего колеса
Она называется уравнением Эйлера или основным уравнением лопастного насоса. Анализ основного уравнения позволяет установить, что напор центробежного насоса.

Очевидно, что в осевых насосах геометрическое подобие подразумевает равенство углов установки лопастей рабочего колеса.
Применительно к осевым и центробежным насосам число Рейнольдса может быть подсчитано различным образом, и каждый раз абсолютные.

К числу лопастных насосов, серийно выпускаемых отечественной промышленностью и
Работа этих насосов основана на общем принципе — силовом взаимодействии лопастей
Центробежные насосы. Основным рабочим органом центробежного насоса, является.