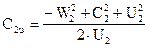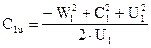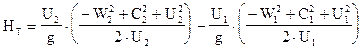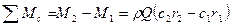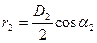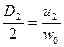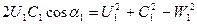Уравнение эйлера для лопастных машин

В процессе проектирования любой лопастной машины необходимо установить взаимосвязь между основными рабочими параметрами машины (подача, напор) и геометрическими размерами, формой лопастей, частотой вращения рабочего колеса. В осевых машинах эту задачу решают с помощью вихревой теории Н.Е. Жуковского. Применительно к центробежным машинам пользуются одноразмерной, струйной теорией, предложенной в 1754 г. Л. Эйлером. Используя закон об изменении моментов количества движения, он получил уравнение для простейшей гидравлической машины – Сегнерова колеса, состоящего из отдельных трубок, траектории движения частиц в которых определялись формой канала-трубки.

При выводе уравнения Эйлером были сделаны два допущения:

· рабочее колесо состоит из бесконечно большого числа бесконечно тонких лопастей;

· рабочее колесо работает без потерь.

При таких допущениях можно без знаний процессов, происходящих внутри каналов рабочего колеса, получить необходимые соотношения по параметрам потока на входе и выходе из него.

Величины, относящиеся к условиям входа в рабочие колесо, обозначим индексом 1, а выхода — индексом 2.

Для вывода уравнения воспользуемся теоремой об изменении момента количества движения: производная по времени от главного момента количества движения системы материальных точек относительно некоторой оси равна сумме моментов всех внешних сил, действующих на данную систему.

(13)

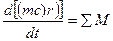
N — мощность на валу рабочего колеса;

m — секундная масса жидкости;

— угловая скорость рабочего колеса;

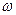
М — внешний момент (на валу рабочего колеса)

М₁— момент количества движения массы жидкости на входе в рабочее колесо;

М₂ — момент количества движения массы жидкости на выходе из рабочего колеса;

N — частота вращения вала рабочего колеса;

Н_т— теоретический напор при бесконечно большом числе лопастей.

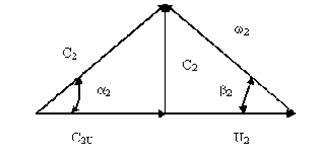
Из плана скоростей при вращении рабочего колеса по часовой стрелке следует:

, (14)

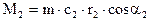
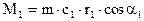
Согласно закону об изменении момента количества движения массы жидкости можно записать:

M = M₂ — M₁ = m×(r₂×c_2u — r₁×c_1u) = 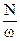. (15)

Известно, что r₁×w = u₁, r₂×w = u₂, M = 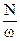(16)

Умножим левую и правую части уравнения на w, а величину мощности выразим r×g×Q_T×H_T

Тогда, решая уравнение относительно Н_т, получим

, м. (17)

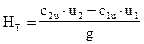
Анализ этого уравнения показывает, что увеличить напора насоса можно разными путями:

1. путем увеличения окружной скорости на выходе из колеса u₂. Для этого можно увеличивать количество оборотов и диаметр рабочего колеса, т.к. ;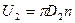

2. путем уменьшения угла a₂. При этом величина проекции абсолютной скорости движения жидкости на окружную

С_2И= U₂ 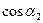будет увеличиваться. Теоретически максимальное значение С_2И= U₂ будет при угле a₂ =0, но при этом подача насоса будет равна нулю. Поэтому при конструировании центробежных насосов чаще всего принимается a₂ =8…12 0 .

3. при неизменных параметрах потока на выходе из рабочего колеса напор насоса можно увеличить путем уменьшения U₁ С_1u. Величину U₁ уменьшать не имеет смысла, потому что при этом еще больше уменьшится величина U₂. Поэтому при конструировании насосов стремятся уменьшить величину С_1u.

Для случая радиального входа жидкости в рабочее колесо, когда a₁=90 и С_1u=0, уравнение Эйлера принимает вид

(18)

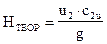
Принимая во внимание, что U₂=p×D₂×n₂ формулу (1) можно записать в виде

(19)

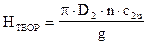
Исходя из этого за счет D₂, n и C_2u можно получить сколь угодно большой напор. Однако в реальных условиях из-за ограничения перечисленных величин повышение удельной энергии на одном колесе насоса не превосходит 5000. 7000 Дж/кг, что соответствует напору 500. 700 м. Диаметр рабочего колеса помимо условий прочности ограничивается потерями на трение его дисков о жидкость. Частота вращения рабочего колеса лимитируется условиями прочности вала и явлением кавитации, которая может возникнуть при больших скоростях жидкости.

При конечном числе лопастей эпюра относительных скоростей в каналах рабочего колеса получится неравномерной, следовательно, будет иметь место разность давлений по обе стороны стенок лопастей. К этому следует добавить, что на характер распределения скоростей в реальном потоке оказывает влияние также форма каналов и вязкость жидкости. Суммарное влияние этих факторов учесть теоретически не представляется возможным. Чтобы применить к реальным потокам и реальным рабочим колесам результаты, полученные на основании струйной теории Л.Эйлера, вводятся опытные поправочные коэффициенты.

Теоретически напор при бесконечном числе лопаток больше напора при конечном числе лопаток и влияние числа лопастей учитывается коэффициентом Г.Ф.Проскуры

, (20)

, (21)

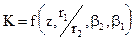
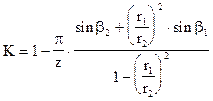
где z — количество лопаток в рабочем колесе, шт.

Обычно у центробежных насосов Z = 6. 12 при этом К = 0.75. 0.9.

Потери напора в насосе характеризуются гидравлическим КПД, который принимается равным 0.8. 0.95.

Действительный напор насоса равен

Пользуясь уравнением Эйлера, определим из каких частей, слагается теоретический напор насоса. Преобразуем уравнение таким образом, чтобы в него после исключения С_2u и С_1u вошли относительные, переносные и абсолютные скорости на входе и выходе из колеса. Из треугольника скоростей на основании теоремы косинусов следует:

(23)

(24)

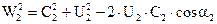
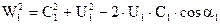
Находим из уравнений

Подставим полученные уравнения в уравнение Эйлера (17)

После преобразований получим

(25)

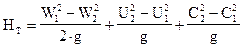
Сумма первых двух членов уравнения называется статическим напором H_т.ст, а третий член уравнения называется динамическим напором H_т.дин. Для уменьшения потерь энергии в процессе преобразования динамического напора в статический последний должен составлять не менее 75. 85% от полного напора. Отношение статического напора к полному напору носит название коэффициента реактивности

(26)

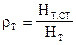
Коэффициент реактивности определяется углом b₂, чем больше r_т, тем большая часть напора преобразуется в рабочем колесе в статический напор.

Дата добавления: 2016-09-26 ; просмотров: 4342 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Дифференциальное уравнение Эйлера. Основное уравнение гидростатикиСкачать

Уравнение Эйлера для работы лопастного колеса

Для определения суммарного момента реакции лопаток рабочего колеса при взаимодействии их с потоком жидкости воспользуемся теоремой об изменении момента количества движения. Согласно этой теореме при установившемся движении изменение момента количества движения потока жидкости, проходящее через рабочее колесо нагнетателя в единицу времени, равно моменту сил реакции лопаток.

Применяя данную теорему к движению жидкости через рабочее колесо нагнетателя, допустим, что это движение установившееся, струйное, без гидравлических потерь. Рассмотрим изменение момента количества движения, массы жидкости за 1с. При этом масса участвующей в движении жидкости можно определить по следующей зависимости:

(2.15)

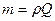
где, – плотность жидкости;

Q – подача нагнетателя.

Момент количества движения относительно оси рабочего колеса во входном сечении при скорости движения в этом сечении C₁ (рисунок 2.3), можно определить по следующей зависимости:

M₁= Qc₁r₁

А момент количества движения на выходе из рабочего колеса – по следующей зависимости:

M₂= Qc₂r₂

r₁ и r₂ — расстояния от оси колеса до вектора входной и выходной скоростей.

Сумма моментов сил, действующих на лопатку рабочего колеса нагнетателя спроецированных на радиус определяют по следующей зависимости:

, а

(2.16)

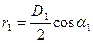
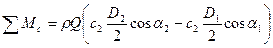
С другой стороны на массу жидкости, заполняющей межлопастные каналы рабочего колеса, действуют 4 группы внешних сил: сила тяжести, силы давления в сечениях (входа-выхода), динамические силы (центробежные силы) со стороны рабочего колеса и силы трения жидкости на обтекаемых поверхностях

где, М_G – момент силы тяжести;

М_P – момент сил давления;

М_К – момент от динамических сил.

Момент силы тяжести всегда равен 0, так как плечо этих сил равно 0 (они проходят через ось вращения колеса). Момент сил давления в расчетных сечениях по той же причине равен 0. А поскольку силами трения пренебрегают, то момент сил трения тоже равен 0. Следовательно, момент всех внешних сил относительно оси вращения колеса сводится к моменту динамического взаимодействия рабочего колеса на протекающую через него жидкость, т.е.

(2.17)

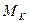
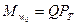
Известно, что мощность, передаваемая жидкости рабочим колесом, т.е. произведение на окружную скорость w₀ равна произведению расхода Q на теоретическое давление P_т, создаваемое нагнетателем.

_, (2.18)

Следовательно, уравнение (2.16) с учетом выражений (2.17) и (2.18) будет иметь вид

(2.19)

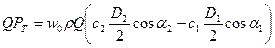
Известно, что окружные скорости u₁ и u₂ можно представить в виде:

(2.20)

из этого следует

_;

Подставив выражения в (2.19) и (2.20) и разделив его на Q, получим

(2.21)

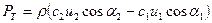
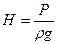
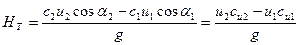
или с учетом того, что или P= gH, уравнение (2.21) примет вид:

(2.22)

Зависимость (2.22) называют основным уравнением лопастных нагнетателей или уравнением Эйлера.

Уравнения (2.21) и (2.22) выведены из условия пренебрежения силами трения и учетом того, что рабочее колесо имеет бесконечное число тонких лопаток (z= ).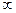

Известно, что в рабочее колеса большинства центробежных нагнетателей жидкость поступает радиально (a=90 0 , следовательно, с₁=0) поэтому уравнение (2.21) и (2.22) можно записать в виде:

(2.23)

(2.24)

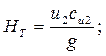
Для осевых нагнетателей в силу того, что переносные (окружные) скорости на входе и выходе одинаковы уравнение (2.22) имеет вид:

(2.25)

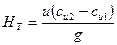
Основное уравнение лопастного нагнетателя показывает, что теоретическое давление и напор, тем больше, чем больше окружная скорость на внешней окружности рабочего колеса u=pD₂n, т.е. чем больше его диаметр, частота вращения и угол b₂.

2.4 Влияние угла (β₂) выхода потока на напор нагнетателя

Угол выхода потока b₂ зависит от формы лопаток. Существуют три вида лопаток: загнутые (по ходу вращения) назад; с радиальным выходом; загнутые вперед.

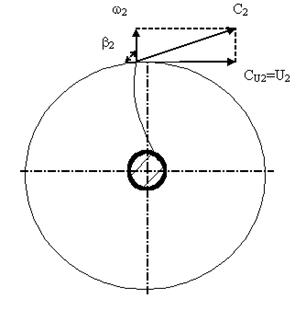
в)

Рис. 2.5. Зависимость угла выходы от формы лопаток.

При равных геометрических размерах колес и постоянном значении u₂ c возрастанием b₂ увеличивается окружная составляющая абсолютной скорости с_w. Следовательно, с увеличением b₂ напор насоса увеличивается и у рабочего колеса с лопатками, загнутыми вперед, он будет наибольшим. Однако в практике насосостроения чаще используют рабочие колеса с лопатками, загнутыми назад. Это объясняется следующими причинами:

1. Основным назначением нагнетателей является создание статистического напора, а колеса с лопатками загнутыми вперед обладают малым коэффициентом статического напора (k_с 0,5), (k= )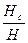

Основное увеличение напора у них происходит за счет возрастания динамической составляющей скорости (с₂).

2. Лопатки, загнутые назад, с гидродинамической точки зрения более удобообтекаемые при переменном режиме работы нагнетателей, диапазон скоростей безотрывного обтекания значительно шире. Следовательно, гидравлические потери при движении жидкой среды по каналам будут меньше, а КПД насоса выше. Обычно принимают следующие значения углов входа и выхода для лопаток, загнутых назад:

Действительное давление и напор, развиваемый нагнетателем, меньше теоретических. Давление, развиваемое нагнетателем, уменьшается главным образом из-за того, что при конечном числе лопастей рабочего колеса не все частицы жидкости отклоняются равномерно, вследствие чего уменьшается абсолютная скорость (с₂). Влияние конечного числа лопастей учитывается введением поправочного коэффициента К,

(2.26)

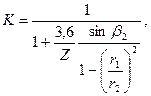
Z – число лопастей рабочего колеса нагнетателя.

Кроме того, часть энергии расходуется на преодоление гидравлических сопротивлений, которые учитываются гидравлическим КПД.

(2.27)

С учетом этих поправок полное давление определяют следующим выражением:

(2.28)

(2.29)

Угол a₂ принимают обычно в пределах 8-14 0 .

Полное давление (напор) можно выразить в виде зависимости от абсолютной, переносной и относительной скоростей потока. Для этого еще раз воспользуемся треугольником скоростей (см. рис.2.4)

Согласно теореме косинусов имеем:

(2.30)

и подставив в уравнение (2.69), вместо значения

(2.31)

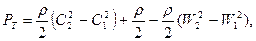
Из уравнения видно, что давление, создаваемое нагнетателем, складывается из прироста кинетической энергии абсолютного движения, повышения статического давления от работы центробежных сил и преобразования кинетической энергии относительного движения в межлопасных каналах.

Отношение скорости закручивания к окружной скорости называется коэффициентом закручиванияj.

Отношение полного давления P_Т к динамическому P_d= , где скорость потока равна окружной скорости U₂, получило название коэффициентаполного давления ψ, который определяют опытным путем.

Видео:Как работает центробежный насос? Основные типы конструкций центробежных насосовСкачать

Динамика м кинематика потока газа в центробежных и осевых компрссорах

Видео:Уравнение Эйлера - bezbotvyСкачать

Основные уравнения газодинамики

Движение газового потока в проточной части лопастных компрессоров имеет сложный пространственный характер. Параметры потока (скорость, давление, плотность, температура) в различных сечениях имеют разные значения и зависят от времени. Обычно же с целью упрощения течение газа в компрессоре принимается установившимся, т. е. независимым от времени. Для вывода основных уравнений движения газа в лопастном компрессоре исходят из представления элементарной струйки газа, у которой в любом поперечном сечении изменением вышеназванных параметров можно пренебречь.

В теории лопастных компрессоров большое значение имеют уравнения постоянства массового расхода (уравнение неразрывности), количества движения и момента количества движения и уравнение энергии в абсолютном и относительном движении.

Уравнение количества движения

Фундаментальная теорема механики — импульс внешней силы равен изменению количества движения материальной системы — применительно к потоку газа в каналах лопастной машины может быть выражена уравнением,
где Р — сила, действующая со стороны потока на лопасть; G — массовый секундный расход; сть стг — средние значения скоростей в начальном и конечном сечениях.

Уравнение моментов количества движения

где М — момент, прилагаемый к массе газа G, необходимый для увеличения момента количества движения; r1, r2—соответственно радиусы начального и конечного сечений потока; с — проекции абсолютных скоростей в этих сечениях на направление окружных скоростей.

Уравнение энергии в абсолютном и относительном движении

Механический принцип рабочих процессов лопастных динамических машин, подающих непрерывную среду (жидкость или газ), одинаков: лопасти, взаимодействуя с потоком, повышают его энергию. Однако жидкость почти несжимаема, а газ сжимаем существенно, и его плотность определяется зависимостью от давления и температуры. Это обстоятельство, а также большое различие в процессах трения жидкостей и газов приводят к существенному различию физических процессов лопастных машин для сжимаемых и несжимаемых сред. В рабочих процессах лопастных компрессоров имеют место термодинамические явления.

Из уравнения следует, что энергия, сообщенная газу, расходуется на сжатие и изменение кинетической энергии газа. Член представляет собой статический напор лопастного компрессора. При течении газа в неподвижном канале, где энергия газу не сообщается и потери пренебрежимо малы.

Уравнение (4.6) называют уравнением Бернулли для установившегося абсолютного движения газа в неподвижном канале. Каналы проточной части лопастного компрессора имеют специфическую форму; некоторые из них, например межлопастные каналы рабочего колеса, вращаются.

Поэтому использование уравнений теоретической газомеханикидля расчета потоков в каналах лопастного компрессора должно проводиться с учетом их особенностей и в некоторых случаях с применением опытных коэффициентов.

Видео:Центробежный насос - устройство и принцип работыСкачать

Течение идеального газа в .межлопастных каналах колеса центробежного компрессора

Кинематика потока в центробежном колесе

Все лопасти рабочего колеса центробежного компрессора можно рассматривать как круговую решетку, вращающуюся с угловой скоростью. До настоящего времени газодинамика потока в таких решетках с конечным шагом лопастей недостаточно изучена. Поэтому применяются упрощенные схемы, рассматривающие течение потока в отдельных межлопастных каналах, образованных соседними лопастями.

Рассмотрим движение идеального газа во вращающемся канале произвольной формы (рис. 4.1). При постоянной ω относительное движение в межлопастных каналах можно полагать установившимся.

Абсолютная скорость с в таком потоке представляет собой векторную сумму относительной W (относительно стенок канала) и переносной (вращение вокруг оси колеса) скорости. Окружная (переносная) скорость на произвольном радиусе равна u = rw. W определяют по объемному расходу q через канал и геометрическим размерам живого сечения канала.

Результирующую абсолютную скорость с определяют построением параллелограмма скоростей. Как будет указано ниже, энергетические качества рабочего колеса определяются главным образом кинематическими соотношениями на входе 1 и выходе 2 рабочего колеса. Обычно вместо параллелограммов строят треугольники скоростей (рис. 4.2).

Составляющая абсолютной скорости сы характеризует закрутку потока при входе на лопасти. Иногда в компрессорах имеет место радиальный (без закрутки) вход потока на лопасти (рис. 4.2), треугольник скоростей для такого случая изображен штриховыми линиями. Составляющая С характеризует энергию, передаваемую газу в рабочем колесе центробежного компрессора. Радиальные составляющие абсолютной скорости определяют объемный расход на входе в колесо и выходе из него.

Механизм передачи энергии в центробежном рабочем колесе

Силовые поля потоков во вращающихся и неподвижных каналах различны.

Кроме сил, вызванных изменением величины и направления W, здесь возникает центробежная сила, вызываемая вращением в переносном движении и сила инерции, вызываемая кориолисовым ускорением. Следовательно, уравнение Бернулли в виде (4.6) в данном случае неприемлемо. К этому уравнению необходимо добавить члены, учитывающие упомянутое различие силового поля.

Равновесие сил, действующих на частицу идеального газа в направлении касательной к ее траектории s в относительном движении по принципу Даламбера, выражается уравнением,
где s — длина пути частицы; р — угол перемещения частицы в относительном движении.

Силы Кориолиса и силы, обусловленные давлением, в направлении оси п, а также сила, возникающая от поворота потока в относительном движении, направлены нормально к траектории и в условии равновесия не учитываются. Сила массы газа также не учитывается вследствие ее малости (рис. 4.1).

Видео:Эффект Вентури и трубка Пито (видео 16) | Жидкости | ФизикаСкачать

Степень реактивности колеса центробежного компрессора

Как следует из уравнения Эйлера, теоретический напор колеса центробежного компрессора зависит от значений u и c (при с = 0).

Для обеспечения требуемого значения действительного напора Я приходится применять различные формы лопастей рабочего колеса, обеспечивающие различные значения С2и при заданной иг. Величина игСги изменяется в широких пределах. При расчете компрессоров проектант должен знать, какую долю составляет потенциальная энергия в общей энергии, передаваемой газу в рабочем колесе. Это отношение называют степенью реактивного р и при c = 0 определяют выражением.

Отношение и угол потока на выходе из рабочего колеса в значительной степени определяют значения H и р (рис. 4.3). С увеличением С возрастает величина H.

Для предельного случая рабочее колесо создает максимальный теоретический напор в форме динамического (р = 0). Соотношение С и р зависят от 0β2.

На рис. 4.3 изображены три возможные формы лопасти при одинаковых β1, D1, D2 и С2г и соответствующее распределение энергий, поКак следует из рис. 4.3, для получения более высоких значений Ят следует выбирать повышенные значения Сги/нг- Однако это допустимо в определенных пределах. При лопастях, загнутых вперед (тип 3), основная часть приращения энергии создается в виде кинетической энергии, что приводит к большим потерям в неподвижных каналах ступени, так как каналы рабочего колеса имеют неблагоприятную форму для потока. Все это снижает КПД компрессора. Кроме того, лопасти, загнутые вперед, имеют неблагоприятные акустические качества. Рабочие колеса с такими лопастями применяются в маломощных вентиляторах. Радиальные лопасти (тип 2) применяются в нагнетателях холодильных центробежных компрессоров. Лопасти, загнутые назад (тип 1), нашли широкое применение в многоступенчатых компрессорах большой мощности.

Видео:Теорема Эйлера о движении жидкостиСкачать

Учет влияния конечного числа лопастей колеса центробежного компрессора

Формулы получены в предположении полной осевой симметрии потока газа в межлопастных каналах рабочего колеса, т.е. при постоянстве скоростей в выходном сечении на окружности диаметра. Это теоретически возможно при бесконечно большом количестве бесконечно тонких лопаток. При этом скорость совпадает с направлением касательной к лопасти. В этом случае суммарное приращение энергии в колесе получается простым суммированием по окружности энергий множества элементарных струек. Схема бесконечного числа лопастей была использована Эйлером и является исходным условием для приближенного определения Hт.

В действительности при конечном числе лопастей картина течения в межлопастных каналах имеет иной вид (см. рис. 4.1).

Согласно гипотезе поток в межлопастном канале можно получить путем сложения двух потоков: потока протекания и потока осевого вихря, интенсивности ω.

При сложении этих потоков (рис. 4. Г) относительная скорость на передней стороне лопасти уменьшается, a на тыльной увеличивается по сравнению со скоростью потока протекания. По уравнению Бернулли происходит изменение давления, что соответствует ранее рассмотренной картине.

В межлопастном канале на входе и выходе имеются окружные составляющие относительных скоростей.

Коэффициент р зависит от многих факторов. Несмотря на многочисленные попытки, не удалось до настоящего времени получить вполне строгое общее выражение для определения μ. Используют приближенные полузначения коэффициента р, колеблются в пределах среднестатической величины (л « 0,8.

С учетом неравномерности распределения скоростей на входе и выходе колеса полная удельная энергия (работа), переданная 1 кг массы газа, которая называется теоретическим -напором Нт, определяется выражением.

Следовательно, для определения удельной энергии, передаваемой потоку рабочим колесом, необходимо знать значения моментов скоростей (циркуляции) на входе и выходе лопастей. Величину моментов определяют экспериментально.

При рассмотрении течения газа во вращающейся круговой решетке за основу принята схема плоского (двухмерного) потока, который наиболее часто встречается в центробежных компрессорах. Если в межлопастных каналах рабочих колес имеет место пространственный (трехмерный) поток, то в этом случае приходится учитывать ряд дополнительных обстоятельств — вторичные течения, перетечки и др.

Одним из способов анализа пространственное™ потока является разбивка полости канала на ряд элементарных полостей, поверхностями вращения Ьимметричными оси колеса. В полученных элементарных полостях поток можно принимать плоским и использовать описанные выше методы.

Видео:Урок 132. Основные понятия гидродинамики. Уравнение непрерывностиСкачать

Внутренний напор ступени центробежного компрессора

Внутренний напор ступени многоступенчатого компрессора Я,- определяет собой полную энергию, сообщенную каждому 1 кг массы газа в ступени компрессора,
где Hт — теоретический напор лопастного колеса; Hд.т — потери напора на дисковое трение; Hд, — потери напора от утечек через уплотнения колеса (Hд. т и Hд, отнесены к 1 кг массы газа).

Потери Hд. т возникают из-за трения в слоях газа близ поверхности дисков рабочего колеса.

Потери в центробежном компрессоре происходят в основном через переднее уплотнение лопастного колеса, в осевом компрессоре — между бандажом колеса и корпусом компрессора (при наличии такового).

Потери взаимно влияют друг на друга, поэтому их разделение весьма условно. (В осевых компрессорах рассмотренные выше потери незначительны, поэтому на практике ими пренебрегают)

В центробежных компрессорах применяют коэффициент закрутки потока.

Коэффициент зависит от числа лопаток и выходного угла лопаток колеса. Суммарный коэффициент, учитывающий относительные потери изменяется в пределах 1,2 ÷ 1,5.

Видео:Турбомашины. Основы теории.Скачать

Параметры профиля и плоской решетки профилей осевого компрессора

Течение газа в пространственных решетках рабочих колес и направляющих аппаратов имеет сложный характер. В теории и расчетах осевых компрессоров используются плоские решетки профилей, которые получаются сечением пространственных решеток рядом соосных цилиндрических поверхностей произвольного радиуса и разверткой полученных сечений на плоскость.

В результате получают плоскую решетку профилей, расположенных на одинаковом расстоянии друг от друга. При ориентировочном рассмотрении течения газа в плоской решетке осевого компрессора (плоский поток) радиальной составляющей скорости газа и взаимным влиянием профилей пренебрегают.

На рис. 4.4,а показана плоская решетка профилей, а на рис. 4.4,б — отдельный профиль. Средняя (скелетная) линия профиля — это кривая линия, разделяющая на равные части расстояние между выпуклой и вогнутой кромкой профиля, измеренное по нормали к этой линии. Среднюю линию можно построить вписанием окружностей в тело профиля. Хордой профиля называют линию, соединяющую крайние точки средней линии. За толщину профиля принимают расстояние между выпуклой и вогнутой кромками профиля, измеренное нормально к хорде, либо расстояние, измеренное нормально к средней линии профиля (т. е. диаметры вписанных окружностей). Кривизна профиля характеризуется углом Ф = θ1 + θ2, где углы θ1 и θ2 — углы между хордой и касательными к средней линии на входё и выходе профиля. Входная и выходная кромки профиля закругляются радиусами r1 и г2.

Все размеры, характеризующие профиль, могут быть представлены как относительные величины путем деления их на длину хорды.

Плоская решетка профилей характеризуется следующими величинами. Шаг решетки это расстояние между соседними профилями, измеренное по соответственным точкам профилей.

Относительный шаг решетки — это отношение шага решетки к длине хорды, т.е. который характеризует густоту решетки.

Ширина решетки — это размер решетки, параллельно оси вала компрессора. Геометрические углы входа и выхода лопастей решетки — это углы между касательными к средней линии профиля на входе и выходе и направлением оси решетки.

Угол установки профиля в решетке — это угол между хордой профиля и осью решетки. Кривизну профиля можно выразить через углы.

Поток газа, обтекающий решетку профилей, характеризуется входным углом β1 и выходным углом β2- Входной угол β1 — это угол между направлением относительной скорости на входе решетки и осью решетки. Выходной угол β2— это угол между направлением относительной скорости на выходе решетки и осью решетки. Разница между углами β2 и β1 называется углом закрутки потока. Угол атаки на входе решетки i—это угол между касательной к средней линии на входе профиля и относительной скоростью.

Угол отставания потока — это угол между касательной к средней линии на выходе профиля и относительной скоростью.

Видео:Принцип работы центробежного насосаСкачать

Силовое взаимодействие между прямолинейной решеткой профилей и потоком газа осевого компрессора. теорема жуковского

При обтекании профиля плоским потоком идеального газа со скоростью вследствие разных давлений на выпуклой и вогнутой сторонах профиля возникает подъемная сила. Подъемная сила перпендикулярна скоростии согласно теореме Жуковского для несжимаемой жидкости определяется на единицу длины профиля уравнением.

Теорема Жуковского действительна и для решетки профилей, если вместо скорости невозмущенного потока в уравнение ввести среднегеометрическую скорость.

КПД решетки

В осевых компрессорах применяются в основном диффузорные решетки, увеличивающие давление газового потока за счет понижения относительной скорости W.

Давление, развиваемое решеткой, работающей на реальном газе, отличается от давления, получаемого в ней прих идеальном газе при прочих равных условиях. Причиной этого является в основном газовое сопротивление межлопастных каналов, требующее для его преодоления определенных затрат энергии. Рассматривая идеальное и реальное течения при одинаковом расходе через решетку, т.е. при одинаковых скоростях на входе и выходе, перепад давлений в реальном потоке отличается от перепада давлений идеального потока, так как в реальном потоке часть перепада расходуется на гидравлические потери.

Видео:Урок 133. Закон Бернулли. Уравнение БернуллиСкачать

Кинематика течения в ступени осевого компрессора

Рассмотрим работу ступени осевого компрессора, состоящей из решеток вращающегося рабочего колеса и неподвижного направляющего аппарата (4.6,а). Сечением решеток ступени соосной цилиндрической поверхностью произвольного радиуса и разверткой получаем плоскую решетку профилей рабочего колеса и направляющего аппарата.

Считая радиальную составляющую скорости незначительной и пренебрегая ее влиянием, получаем равенство меридиональной и осевой составляющей скорости. Плоская решетка рабочего колеса движется с переносной скоростью и = const. Так как с — абсолютная скорость газа перед решеткой рабочего колеса, построив вектор переносной скорости и, получаем вектор относительной скорости с которой газ поступает на вращающуюся решетку колеса. Скорости образуют так называемый входной треугольник скоростей перед решеткой.

Так как W2 — относительная скорость газа на выходе решетки, добавив к ней вектор переносной скорости u1 получаем абсолютную скорость с2 на выходе из решетки. Скорости с2, и, W2 образуют так называемый выходной треугольник скоростей за решеткой.

На входе и выходе решетки рабочего колеса осевые составляющие скорости соответственно сг и сг2. В осевых компрессорах осевая скорость с обычно постоянна либо несколько уменьшается от первой к последней ступени.

На рис. 4.6,б, в показаны совместно скоростные треугольники на входе и выходе решетки рабочего колеса. Здесь же показана среднегеометрическая скорость

Поток газа поступает на решетку направляющего аппарата со скоростью С2 и покидает решетку со скоростью С3, несколько меньшей С2 из-за диффузорного эффекта.

Видео:Закон БернуллиСкачать

Напор ступени осевого компрессора

Теоретический напор осевого компрессора представляет собой энергию, передаваемую лопатками рабочего колеса каждому 1 кг газа, проходящему через него.

Сообщение энергии материальной системе, в том числе газу, возможно только в процессе движения приложением внешней силы. Такой силой для потока газа в межлопастных каналах решетки является подъемная сила, вычисленная по формуле Жуковского.

Для существования такой силы должна иметь место разность давлений на передней и тыльной сторонах лопасти. Если обозначить через давление в середине канала на радиусе, то должно выполняться условие. В результате обтекания газовым потоком лопасти и образования перепада давления на передней и тыльной сторонах лопатки образуется циркуляционный поток. Суммарная циркуляция лопаток равна разности циркуляций на входе в колесо и выходе из него.

Теоретический напор можно выразить через циркуляцию скорости профиля решетки.

Видео:Теоретический напор центробежного насосаСкачать

Основные кинематические схемы осевых компрессоров

В осевых компрессорах степень реактивности обычно лежит в пределах 0,5 ÷ 1,0. При р 1 происходит скачкообразное изменение параметров потока. Обратный переход от сверхзвуковых к дозвуковым значениям скоростей нельзя осуществить плавно. При переходе скорости звука в рабочей среде имеет место скачкообразное изменение параметров потока р, р и Т. Такой процесс называют скачком уплотнения (стоячей ударной волной). Скачок уплотнения сопровождается сильными акустическими явлениями (подобными преодолению звукового барьера самолетом).

При скачке уплотнения происходит резкое снижение КПД компрессора (подобно снижению КПД при кавитации в насосе). Снижение КПД в значительной степени вызвано увеличением сопротивления при обтекании профиля из-за интенсивного отрыва пограничного слоя при скачке уплотнения. При скачках уплотнения происходит необратимое преобразование кинетической энергии газа в теплоту, возникает свойственное только сверхзвуковым потокам волновое сопротивление.

На рис. 4.8 показана качественная картина дозвукового и сверхзвукового обтекания профиля.

Опасность возникновения скачка уплотнений в центробежных компрессорах относительно меньше.

Стационарные компрессоры рекомендуется выполнять при максимальных значениях числа Маха М 0,75 можно принять
ε’ = (1 — М2)ε,
где ε ≈ 8° — оптимальный угол раскрытия диффузора для несжимаемого газа.

Видео:Центробежный насосСкачать

Основы теории подобия. безразмерные коэффициенты

Лопастные компрессоры относятся к классу динамических машин. Явления, происходящие в потоке газа в проточной части, должны подчиняться общим законам динамического подобия. Поток газа в проточной части компрессора движется с высокими скоростями и, следовательно, с высокой степенью турбулентности (в квадратичной зоне режимов течения). В связи с этим условия динамического подобия течения могут выполняться, если обеспечить прежде всего требования геометрического и кинематического подобия.

Компрессоры обычно создаются сериями с геометрически подобной формой проточной части, и рабочие параметры их подчиняются основным законам подобия.

Основные критерии подобия лопастных компрессоров

При изучении подобия газодинамических процессов в лопастных компрессорах рассматриваются следующие безразмерные критерии:

• число Маха — М, характеризующее режим течения при скоростях, превышающих скорость звука в газовой среде, подаваемой компрессором;
• число Рейнольдса — Re, характеризующее режим течения при скоростях, меньших скорости звука;
• число Прандтля — Рг, оценивающее влияние тепломеханических характеристик газа на его движение и теплообмен);
• число Нуссельта — Nu, определяющее влияние теплообмена газа при его движении.

К этим четырем критериям следует добавить показатель адиабаты k. Однако выполнение равенства всех критериев подобия для двух геометрически подобных потоков невозможно.

Например, равенство чисел Re и М возможно лишь в случае, если рассматриваемые системы каналов не только подобны, но и равны по размерам. Для газовых потоков с разными показателями адиабаты невозможно сочетать геометрическое и кинематическое подобие во всех сходственных сечениях двух лопастных компрессоров. Поэтому применяется приближенное подобие, допускающее нарушение таких критериев подобия, которые в данном конкретном случае не являются определяющими.

В неохлаждаемых группах ступеней компрессорных машин процессы теплопередачи существенного значения не имеют, поэтому критерии Прандтля и Нуссельта в этих случаях можно не учитывать. Число Re оказывает влияние на характер течения.

В пределах значений М 0,8);

Необходимо отметить, что число Рr для газов с одинаковыми к (равной атомности) практически одинаковы.

В проточной части компрессора аналитическое определение основных технических характеристик с использованием методов газодинамики довольно сложно. Поэтому если известны характеристики проточной части какого-то компрессора или его ступени (обозначим индексом м), то при выполнении условий подобия можно определить характеристики разрабатываемого компрессора (индекс н).

Масштаб геометрического подобия (коэффициент пересчета)

При широком диапазоне изменения значений Хы и т обеспечить точное соблюдение условий подобия трудно.
В качестве критерия подобия в компрессоростроении используют также коэффициент быстроходности, об/мин.

Под коэффициентом быстроходности подразумевается частота вращения ступени эталонного компрессора (геометрически подобного проектируемому), который, работая на аналогичном газе при производительности VM = 1 м³/с, создает напор Ям = 1 м.

В многоступенчатых компрессорах значение пул меняется из-за изменения объемной производительности по ступеням.

Ступени с равным нуд имеют одинаковые характерные геометрические и кинематические соотношения проточной части и одинаковую безразмерную характеристику. Создаваемые серии компрессоров обычно имеют проточную часть с одинаковым Пуд.

Для энергетической и размерной характеристик ступеней используются безразмерные коэффициенты, которые также зависят от пуд. К ним относятся:

• коэффициент напора (давления). Это коэффициент, характеризующий соотношение между окружной скоростью u2 и действительным напором (повышением давления), не совсем точен, так как не учитывает изменения гидравлического КПД в подобных ступенях различных геометрических размеров. Его используют для приближенных расчетов;
• коэффициент расхода (производительности)
• коэффициент полезной мощности

Коэффициенты определяют пропускную способность, энергоемкость и размеры сечений проточной части серии подобных ступеней и используются для построения безразмерной характеристики для серий подобных машин.

Значения коэффициента ср изменяются в пределах:

• для центробежных компрессоров φ = 0,03 ÷ 0,15;
• для диагональных компрессоров φ = 0,1 ÷ 0,2.

Приняв соответствующие значения φ и имея заданные параметры V, Н и n, можно определить ориентировочно габаритный размер рабочего колеса и требуемое значение u2. По выбранным значениям входной скорости в рабочее колесо (обычно с = 20 ÷ 100 м/с) и коэффициенту φ можно оценить диаметр D0 входной воронки рабочего колеса.

Таким образом, n, φ и ψ служат исходными величинами для определения размеров элементов проточной части центробежного компрессора на заданные параметры.

🔍 Видео

Пуск насосаСкачать

Гидростатическое давлениеСкачать

Подготовка насоса к ремонту и приемка насосов из ремонтаСкачать

Детали машин. Лекция 4.1. Валы и оси.Скачать

Движение жидкости в рабочем колесеСкачать