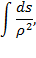Начало исследований изогнутой оси стержня в пределах пропорциональности (упругой линии) было положено в работах Я.Бернулли в 1694 и 1705 гг. [323, 324]. Он изучал прогибы при изгибе консольной балки прямоугольного поперечного сечения, нагруженной силой, приложенной на конце. При этом, так же как и Э.Мариотт, он принимал однозначную (нейтральная линия совпадает со стороной поперечного сечения), а затем и двузначную (нейтральная линия делит поперечное сечение на две равные части) треугольные эпюры напряжений. При этом Я.Бернулли сделал точно такую же ошибку, что и Мариотт, в результате чего пришел к неправильному заключению о том, что положение нейтральной линии не оказывает влияния на форму изогнутой оси. Однако Я.Бернулли правильно установил пропорциональность кривизны изгибающему моменту, хотя и с неправильным коэффициентом пропорциональности. Эта зависимость была использована Л.Эйлером в его работах по исследованию упругих линий.
По совету Я.Бернулли , Эйлер использовал разрабатываемое им вариационное исчисление, составлявшее предмет его книги [307], вышедшей в 1744 г., для вывода уравнений упругой линии. Приложение 1 этой книги, которое посвящено упругим кривым, начинается следующей фразой: «Действительно, так как здание всего мира совершенно и возведено премудрым творцом, то в мире не происходит ничего, в чем не был бы виден смысл какого-нибудь максимума или минимума; поэтому нет никакого сомнения, что все явления мира с таким же успехом можно определить из причин конечных при помощи методов максимума и минимума, как и из самих причин производящих». Дифференциальное уравнение изогнутой оси стержня Эйлер получил из условия минимума интеграла
ds ρ 2 ,
Видео:Дифференциальное уравнение Эйлера. Основное уравнение гидростатикиСкачать

где ds — элемент длины стержня, ρ — радиус кривизны его оси. Сам Я.Бернулли в 1751 г. впервые вывел дифференциальное уравнение поперечных колебаний стержня и рассмотрел ряд частных случаев [322]. Л.Эйлер не ограничился рассмотрением лишь малых прогибов. Он проинтегрировал в рядах дифференциальное уравнение для больших перемещений, в котором не пренебрегается квадратом первой производной прогиба по сравнению с единицей. Л.Эйлер также рассмотрел изгиб консольной балки переменного поперечного сечения, жесткость которой пропорциональна расстоянию от приложенной силы, изгиб консоли, нагруженной равномерно распределенной нагрузкой (собственный вес), и изгиб стержня малой кривизны, полагая, что разница между конечной и начальной кривизной пропорциональна изгибающему моменту. В связи с последней задачей Эйлер установил, какой должна быть начальная (искривленная) форма консоли для того, чтобы после приложения на конце ее силы она стала прямолинейной. При решении всех этих задач Эйлера не интересовал физический смысл постоянной в линейной зависимости кривизны от изгибающего момента.
Большие прогибы консольной балки были исследованы также Б.Сен-Венаном, который решил задачу в рядах. Результаты были опубликованы в третьем издании книги Л.Навье [447]. Б.Сен-Венан также показал, что в случае малых перемещений прогиб консольной балки может быть вычислен методом, который в настоящее время называется методом моментных площадей. В 1771 г. Ж.Лагранж изучал [414] изгиб полосы постоянного поперечного сечения заделанной одним концом и нагруженной на другом конце силой. При этом было использовано точное уравнение изогнутой оси.
Определением прогибов балок на основе интегрирования приближенного дифференциального уравнения для малых перемещений занимался Л.Навье в 1826г. [447], который рассмотрел ряд частных случаев.
Влияние поперечной силы на прогибы балок исследовано Ж.Понселе в 1826 г. [464].
Видео:Уравнение Бернулли гидравликаСкачать

Определению прогибов балок при малых перемещениях посвящено много работ. Наиболее значительной, по-видимому, является книга А.Клебша [344], опубликованная в 1862г. В ней автор указал на способ интегрирования дифференциальных уравнений для балки с несколькими участками, при котором число постоянных интегрирования равно двум при любом числе участков.
Зависимости Ф.Дюпена для прогиба балок
Экспериментальное исследование прогибов деревянных балок производил Ж.Бюффон [331] в 1741 г. Он определял не только разрушающую силу для двухопорных деревянных балок, нагруженных силой, в среднем сечении, но и прогиб в этом сечении в момент разрушения. Ф.Дюпэн также производил испытания двухопорных балок прямоугольного поперечного сечения по той же схеме, что и Ж.Бюффон, и установил, что прогиб прямо пропорционален кубу длины балки и обратно пропорционален ширине поперечного сечения и кубу его высоты. На рисунке изображены полученные Дюпэном графики зависимости прогиба от куба длины пролета при одинаковой силе, приложенной в среднем сечении, и одинаковых размерах поперечного сечения. Сопоставляя наибольшие прогибы балок, нагруженных равномерно распределенной нагрузкой, а затем силой, равнодействующей этой нагрузки, приложенной в среднем сечении, Дюпэн экспериментально установил, что их отношение равно 19/30, что близко к величине 5/8, которую дает теория изгиба. Эти эксперименты описаны в статье Ф.Дюпэна [358], опубликованной в 1815 г. А.Дюло в работе [357], опубликованной в 1820 г., приводит результаты испытаний двухопорных с консолями и без них железных балок — прямоугольного, круглого и треугольного поперечных сечений, нагруженных силой, приложенной в различных сечениях. Он установил, что для прямоугольного и круглого сечений согласование экспериментальных и теоретических результатов по определению прогибов хорошее. В случае треугольного сечения согласование значительно худшее, что, очевидно, объясняется неверным определением положения нейтральной оси.
Изгиб балок на упругом основании обычно в курсах сопротивления материалов не излагается. В некоторых учебниках этому вопросу уделяется внимание. Если принять, что реакция основания в некотором сечении балки пропорциональна прогибу этого сечения, то тогда дифференциальное уравнение изогнутой оси совпадает с дифференциальным уравнением для прогиба при осесимметричном нагружении цилиндрической оболочки и является линейным дифференциальным уравнением четвертого порядка. Предположение о пропорциональности реакции основания прогибу было введено Э.Винклером в 1867 г. [503]. Основание, обладающее таким свойством, иногда называют винклеровым.
Видео:Урок 133. Закон Бернулли. Уравнение БернуллиСкачать

Заметим, впрочем, что для случая односторонних связей (например, плавающая в жидкости балка, корпус судна) эта гипотеза была предложена в 1778 г. [365] математиком Николаем Ивановичем Фуссом (29.01.1755 — 23.12.1825).
Механик и инженер Анри Эме Резаль (27.01.1828 — 22.08.1896) в 1876г. применил указанное выше линейное дифференциальное уравнение четвертого порядка для расчета стенки парового котла [471]. Использование этого уравнения для различных задач строительной механики принадлежит В.Г.Шухову, опубликовавшему в 1903г. работу [306]. В частности, он применил указанное уравнение в расчетах резервуаров для хранения нефти. По-видимому, В.Г.Шухов установил последовательные дифференциальные соотношения между прогибом балки, углом поворота сечения, изгибающим моментом, поперечной силой и интенсивностью распределенной нагрузки. Идея метода начальных параметров в расчете балок на упругом основании была впервые предложена в 1902г. механиком и инженером Дмитрием Константиновичем Бобылевым (11.11.1842 — 20.02.1917) в его книге [132].
Механик и инженер Нестор Платонович Пузыревский (30.08.1861 — 26.08.1934) развил этот метод в своем литографированном курсе оснований и фундаментов, опубликованном в 1923г. [236]. Однако работы Д.К.Бобылева и Н.П.Пузыревского не привлекли к себе внимания и остались незамеченными. В 1930 г. А.Н.Крылов опубликовал монографию [192], в которой было дано исчерпывающее изложение метода начальных параметров, причем рассмотрены как балки постоянного, так и балки переменного поперечных сечений и приведены примеры использования метода, в частности, для расчета связей и набора судового днища.
Изгиб кривых стержней малой кривизны при малых перемещениях изучал Л.Навье [447] в 1826 г. Он, так же как и Л.Эйлер, принимал, что изменение кривизны прямо пропорционально изгибающему моменту, но в отличие от работы Л.Эйлера коэффициент пропорциональности был определен как величина, обратная жесткости стержня при изгибе.
Видео:Теорема Эйлера о движении жидкостиСкачать

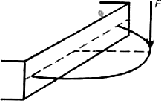
Б.Сен-Венан исследовал изгиб кривого стержня малой кривизны, введя в формулы Л.Навье дополнительные члены, учитывающие перемещения, вызываемые удлинением оси стержня, а также сдвигом. В качестве примера он решил задачи плоского изгиба круглого кольца, подвешенного в некоторой точке, под действием его сил тяжести, а также плоского изгиба кольца под воздействием двух сжимающих кольцо сил. Кроме этого, Сен-Венан решил задачу изгиба кривого стержня в виде полуокружности из его плоскости. Все эти результаты, полученные Сен-Венаном, изложены в его мемуарах [475], опубликованных в 1844 г.

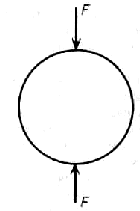
Задачи исследования изгиба бруса малой кривизны, исследованные Сен-Венаном
Общая теория больших перемещений в пределах упругости прямых и кривых стержней малой кривизны в одной плоскости разработана механиком и инженером Евгением Павловичем Поповым (14.02.1914) и отражена в его монографиях [232, 233], опубликованных в 1947—1948 гг. и удостоенных в 1949 г. Государственной премии. В них изложена не только теория плоского изгиба прямых и кривых стержней малой кривизны при больших перемещениях, но и приведено значительное количество конкретных задач и числовых примеров.
Составленные автором таблицы и диаграммы освобождают конструкторов от утомительных вычислений.
Видео:Балка на трёх опорахСкачать

Более полное изложение этой теории дано в книге Е.П.Попова [234], опубликованной в 1986 г. В ней приведены общие формулы, которые являются едиными при больших прогибах, как прямых, так и кривых стержней малой кривизны, независимо от схем нагружения и условий закрепления. Структура этих формул, а также таблиц и диаграмм такова, что точность расчета увеличивается с возрастанием перемещений, что является очень ценным свойством метода.
Дифференциальные уравнения равновесия пространственного кривого стержня, нагруженного на торцах силами, были получены Р.Кирхгофом [404] в 1858 г. Он же установил аналогию между задачей об упругой линии для стержня, ось которого в недеформированном состоянии прямолинейна, и задачей о вращении тяжелого твердого тела вокруг неподвижной точки.
Уравнения Кирхгофа были дополнены зависимостями, описывающими малые перемещения стержня, установленными А.Клебшем [344] в 1862 г., и таким образом была получена система уравнений (Кирхгофа—Клебша), которая вместе с уравнениями, выведенными на основе закона Гука, позволила решать задачи малых перемещений пространственных кривых стержней.
Исследованию упругой линии двоякой кривизны посвящена работа Е.Л.Николаи, опубликованная в 1816 г. [216].
Видео:Урок 134. Применения уравнения Бернулли (ч.1)Скачать

Для пространственных криволинейных стержней произвольной формы алгоритм определения усилий и моментов, линейных и угловых перемещений дан в статье механика и инженера Анатолия Петровича Филина (05.12.1920) [292].
Статике и динамике пространственных криволинейных стержней посвящены книги механика и инженера Валерия Александровича Светлицкого (01.06.1927), опубликованные в 1978и 1987гг. [251, 252]. Статике таких стержней посвящены также опубликованные в 1979 и 1984 гг. монографии механиков Александра Алексеевича Илюхина [177] и Юрия Борисовича Шулькина [305].
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
📺 Видео
Закон БернуллиСкачать

10. Уравнения БернуллиСкачать

Уравнение Бернулли для потока жидкостиСкачать

Понимание напряжений в балкахСкачать

Уравнение Бернулли. Практическая часть. 10 класс.Скачать

Дифференциальные уравнения, 5 урок, Уравнение БернуллиСкачать

Уравнение Бернулли Метод БернуллиСкачать

Уравнение БернуллиСкачать

Уравнение Эйлера - bezbotvyСкачать

Уравнение Бернулли. Диаграмма Бернулли.Скачать

Урок 132. Основные понятия гидродинамики. Уравнение непрерывностиСкачать

История изучения кровотока, 18 - нач. 19 века. Гемодинамика: Эйлер, Бернулли, Пуазёйль.Скачать

Уравнение БернуллиСкачать

Галилео. Эксперимент. Закон БернуллиСкачать