Видео:Полярная система координатСкачать

Параметрические уравнения эвольвенты окружности
Два твердых тела (звена), соприкасающиеся своими поверхностями и имеющие возможность двигаться относительно друг друга, образуют кинематическую пару. Кинематическая пара допускает не любое движение звеньев относительно друг друга, а только такое движение, которое согласуется с характером соприкосновения и с формой соприкасающихся поверхностей.
Если звенья, образующие КП, в силу характера их соприкосновения, могут совершать только простейшие движения относительно друг друга ( вращательное, прямолинейное поступательное или, в общем случае, винтовое ), то пара является низшей . Низшая пара — пара, в которой требуемое относительное движение звеньев обеспечивается соприкасанием ее элементов по поверхности ( фактическое соприкасание звеньев в низшей паре возможно как по поверхности, так и по линиям и точкам ). В таких парах движение одного звена относительно другого представляет собой чистое скольжение, причем может иметь место поверхностный контакт — соприкасание звеньев по плоскости, цилиндрической или винтовой поверхности. Такая поверхность контакта может двигаться, «как бы оставаясь в самой себе».
Более сложные относительные движения можно реализовать в парах, характер соприкасания звеньев в которых допускает не только относительное скольжение, но и перекатывание. Такие пары называются высшими. Высшая пара — пара, в которой требуемое относительное движение звеньев может быть получено только соприкасанием звеньев по линиям или в точках. В высшей паре поверхностный контакт невозможен, так как он исключает возможность перекатывания тел. Если контакт в высшей КП происходит по линии, то она называется мгновенной контактной линией. Эта линия может быть прямой или кривой, при движении соприкасающихся тел она не только меняет свое положение по отношению к звеньям и к неподвижному пространству, но может менять и свою форму. Двигаясь относительно каждого из соприкасающихся звеньев, эта линия как бы «покрывает», описывает или формирует его поверхность. То есть поверхность каждого из звеньев пары можно рассматривать как геометрическое место мгновенных контактных линий в системе координат, связанной со звеном. В неподвижном пространстве эти линии описывают поверхность зацепления — геометрическое место мгновенных контактных линий в неподвижной системе координат. Очевидно, что мгновенная контактная линия — линия пересечения поверхности зацепления с любой из двух соприкасающихся поверхностей. При точечном контакте, контактная точка в системах координат связанных со звеньями описывает некоторую контактную линию на контактирующей поверхности, в неподвижной системе координат — линию зацепления.
Как следует из вышеизложенного, характер относительного движения звеньев КП и геометрия их контактирующих поверхностей находятся в тесной взаимосвязи. Изучение геометрии контактирующих поверхностей в связи с их относительным движением составляет предмет раздела прикладной механики, который называется теорией зацепления [ 1, 2 ].
Механизмы с высшими кинематическими парами и их классификация.
К механизмам с высшими КП относятся любые механизмы в состав которых входит хотя бы одна высшая пара. Простейший типовой механизм с высшей парой состоит из двух подвижных звеньев, образующих между собой высшую кинематическую пару, а со стойкой низшие ( вращательные или поступательные ) пары. К простейшим механизмам с высшей парой относятся :
Структурные схемы простейших механизмов с высшими КП..
Фрикционными механизмами или передачами сцепления называются механизмы с высшей парой в которых передача движения в высшей паре осуществляется за счет сил сцепления или трения в зоне контакта. Кулачковым механизмом называется механизм с высшей парой, ведущее звено которого выполнено в форме замкнутой криволинейной поверхности и называется кулачком (или кулаком). Зубчатыми механизмами называются механизмы звенья которых снабжены зубьями (зубчатый механизм можно определить как многократный кулачковый, рассматривая зацепление каждой пары зубьев, как зацепление двух кулачков) . Рабочие поверхности зубьев должны быть выполнены так, чтобы обеспечивать передачу и преобразование движения по заданному закону за счет их зацепления . Условия, которым должны удовлетворять рабочие поверхности высших пар, формулируются в разделе теории механизмов — теории зацепления или теории высшей пары.
Основы теории высшей кинематической пары.
Основная теорема зацепления.
Понятие о полюсе и центроидах. Рассмотрим два твердых тела i и j , которые совершают друг по отношению к другу плоское движение. Свяжем с телом i систему координат 0 i x i y i , а с телом j систему координат 0 j x j y j . Плоское движение тела i относительно тела j в рассматриваемый момент эквивалентно вращению вокруг мгновенного центра скоростей или полюса P . Тогда геометрическое место полюсов относительного вращения в системе координат 0 i x i y i называется подвижной Ц i , а в системе координат 0 j x j y j неподвижной Ц j центроидой. В процессе рассматриваемого движения цетроиды контактируют друг с другом в полюсах относительного вращения и поэтому перекатываются друг по другу без скольжения, т.е.
V Pi = V Pj ; V PiPj = 0 ;
тогда дуга S wi равна дуге S wj .
Полюс зацепления — мгновенный центр относительного вращения звеньев, образующих кинематическую пару.
Центроида (полоида) — геометрическое место центров (полюсов) относительного вращения в системах координат, связанных со звеньями.
Передаточное отношение для тел совершающих вращательное движение.
Рассмотрим два тела 1 и 2 , совершающих вращательное движение соответственно вокруг центров 0 1 и 0 2 с угловыми скоростями w 1 и w 2 (рис. 11.6). Причем нам неизвестно связаны эти тела между собой или нет. Как отмечено выше, полюс относительного вращения этих тел будет лежать в такой общей точке этих тел , где вектора скоростей как первого, так и второго тела будут равны. Для скоростей любой точки первого тела V A = w 1 Ч l A01 , для любой точки второго — V В = w 2 Ч l В 02 . Равенство векторов скоростей по направлению для тел, совершающих вращательное движение, возможно только на линии соединяющей центры вращения тел. Поэтому полюс относительного вращения должен лежать на этой линии . Для определения положения полюса на линии центров составим следующее уравнение
| Движение механизма: | Звено 1 | Звено 2 | Звено 0 |
| исходное | w 1 | w 2 | w 0 = 0 |
| относительно звена 1 | w 1 — w 1 = 0 | w 21 = w 2 — w 1 | w 1 = — w 01 |
Скорость любой точки звена 2 в относительном движении будет равно его угловой скорости в этом движении умноженной на расстояние от этой точки до полюса относительного вращения, т. е.
Перейдем к рассмотрению двух тел 1 и 2 , совершающих вращательное движение, соответственно вокруг центров 0 1 и 0 2 с угловыми скоростями w 1 и w 2 , и образующих между собой высшую кинематическую пару К (рис. 11.7).
Условием существования высшей кинематической пары является условие неразрывности контакта звеньев, которое заключается в том, что проекции скоростей звеньев в точке контакта на контактную нормаль к профилям должны быть равны
т.е. скалярное произведение вектора относительной скорости в точке контакта на орт нормали равно нулю. Это условие обеспечивается, если скорость относительного движения контактных точек лежит на касательной ( в пространстве в касательной плоскости ). При выполнении этого условия профили не отстают друг от друга ( нарушение контакта приведет к исчезновению пары ), и не внедряются друг в друга
( что при принятом допущении о абсолютно жестких звеньях, невозможно ).
Как было показано выше скорость относительного скольжения в точке контакта равна
где l KP — расстояние от контактной точки до полюса относительного вращения. Так как V K2K1 перпендикулярна l KP >, а V K2K1 должна лежать на касательной, то l KP является нормалью к профилям в точке контакта. То есть контактная нормаль к профилям в высшей паре пересекает линию центров в полюсе относительного вращения.
Основная теорема зацепления.
Формулировка анализа. Контактная нормаль к профилям высшей пары пересекает линию центров в полюсе относительного вращения звеньев ( то что полюс делит линию центров на отрезки обратно пропроциональные угловым скоростям было доказано выше ).
Формулировка синтеза. Профили в высшей кинематической паре должны быть выполнены так, чтобы контактная нормаль к ним проходила через полюс относительного вращения звеньев.
Так как положение полюса на линии центров определяет передаточное отношение механизма, то профили удовлетворяющие основной теореме зацепления обеспечивают заданный закон изменения передаточного отношения или являются сопряженными.
Скорость скольжения в высшей КП или перовое следствие основной теоремы зацепления.
Скорость скольжения профилей в высшей КП равна произведению скорости относительного вращения на расстояние от контактной точки до полюса зацепления.
где верхний знак относится к внешнему зацеплению, нижний — к внутреннему. Зацепление считается внешним, если полюс делит линию центров внутренним образом и направления угловых скоростей звеньев противоположны, и внутренним, если полюс делит линию центров внешним образом (Рис. 17.8) и направления угловых скоростей одинаковы.
Из формулы видно, что скорость скольжения во внутреннем зацеплении много меньше, чем во внешнем.
Определение центра вращения ведущего звена или второе следствие основной теоремы зацепления.
Из схемы, изображенной на рис. 11.7, видно, что
т.е. отрезок l KD , отсекаемый от луча, проведенного из точки О 2 через точку K, прямой параллельной контактной нормали, равен передаточной функции точки K 2 .
Второе следствие основной теоремы зацепления.
Формулировка синтеза. Если на продолжении луча, проведенного из точки О 2 через точку K, отложить от точки K отрезок длиной l KD = V K2 / w 1 = V qK2 и через конец этого отрезка провести прямую параллельную контактной нормали, то эта прямая пройдет через центр вращения ведущего звена точку О 1 .
С использованием этого свойства механизма с высшей парой при проектировании кулачковых механизмов определяют радиус начальной шайбы по допустимому углу давления.
Формулировка анализа. Луч проведенный через центр вращения ведущего звена точку О 2 параллельно контактной нормали, отсекает на луче проведенном из точки О 2 через точку K отрезок l KD = V K2 / w 1 = V qK2 , равный передаточной функции точки K 2 .
Угол давления в высшей паре ( на примере плоского кулачкового механизма ).
Рассмотрим плоский кулачковый механизм с поступательно движущимся роликовым толкателем ( Рис. 11.9). Из D BPF
Подставляя эти выражения в формулу для тангенса угла давления, получим
где знак — соответствует смещению оси толкателя (эксцентриситету) вправо от центра вращения кулачка.
Теорема Оливье имеет три важных следствия:
Следствие 1. Если оба зубчатых колеса обработаны друг другом, т.е. первое колесо обработано инструментом режущие кромки которого копируют второе колесо, а второое — инструментом режущие кромки которого копируют первое, то эти колеса имеют взаимоогибаемые поверхности зубьев с линейным контактом поверхностей.
Следствие 2. Если оба колеса обработаны инструментами, образующими между собой конгруентную пару, то эти колеса имеют взаимоогибаемые поверхности зубьев с линейным контактом поверхностей.
Следствие 3. Если поверхность зацепления И 1 инструмента 1 с колесом 1 и поверхность зацепления И 2 инструмента 2 с колесом 2 совпадает с поверхностью зацепления колес 1 и 2, то зубья колес обработанных при таком условии будут иметь линейный контакт.
Зубчатые передачи и их классификация.
Зубчатыми передачами называются механизмы с высшими кинематическими парами в состав которых входят зубчатые колеса, рейки или секторы — звенья, снабженные профилироваными выступами или зубьями. Зубчатые передачи бывают простые и сложные. Простая зубчатая передача — трехзвенные механизм, состоящий из двух зубчатых колес и стойки, в котором зубчатые колеса образуют между собой высшую пару, со стойкой — низшие ( поступательные или вращательные ).
Простые зубчатые передачи классифицируются:
- с постоянным передаточным отношением;
- с переменным передаточным отношением;
- с параллельными осями;
- с пересекающимися осями;
- с перекрещивающимися осями;
- эвольвентным профилем;
- с циклоидальным профилем;
- с круговым профилем (передачи Новикова);
- с прямым зубом;
- косозубые;
- шевронные;
- с круговым зубом;
- цилиндрические;
- коническое;
- гиперболоидные;
- червячные;
- с некруглыми колесами;
- винтовые.
Эвольвентная зубчатая передача.
Эвольвентная зубчатая передача — цилиндрическая зубчатая передача, профили зубьев которой выполнены по эвольвенте окружности.
Эвольвента окружности и ее свойства.
Эволютой называется геометрическое место центров кривизны данной кривой. Данная кривая по отношению к эволюте называется эвольвентой. Согласно определению нормаль к эвольвенте ( на которой лежит центр кривизны ) является касательной к эволюте. Эвольвенты окружности описываются точками производящей прямой при ее перекатывании по окружности, которую называют основной.
Свойства эвольвенты окружности:
Форма эвольвенты окружности определяется только радиусом основной окружности r b . При 
Производящая прямая является нормалью к эвольвенте в рассматриваемой произвольной точке M y . Отрезок нормали в произвольной точке эвольвенты l MyN = r равен радиусу ее кривизны и является касательной к основной окружности.
Эвольвента имеет две ветви и точку возврата М 0 , лежащую на основной окружности. Эвольвента не имеет точек внутри основной окружности.
Точки связанные с производящей прямой но не лежащие на ней при перекатывании описывают: точки расположенные выше производящей прямой W — укороченные эвольвенты, точки, расположенные ниже производящей прямой L — удлиненные эвольвенты.
Параметрические уравнения эвольвенты получим из схемы, изображенной на рис. 11.11 . Так как производящая прямая перекатывается по основной окружности без скольжения то дуга М 0 N равна отрезку NM y . Для дуги окружности
из треугольника D OM y N
получим параметрические уравнения эвольвенты.
Эвольвентное зацепление и его свойства.
В зубчатой передаче контактирующие элементы двух профилей выполняются по эвольвентам окружности и образуют, так называемое эвольвентное зацепление. Это зацепление обладает рядом полезных свойств, которые и определяют широкое распространение эвольвентных зубчатых передач в современном машиностроении. Рассмотрим эти свойства.






















































































 откуда
откуда 





 3) Радиус кривизны эвольвенты в данной точке равен отрезку производящей прямой, заключённому между данной точкой эвольвенты и точкой касания производящей прямой с основной окружностью, ρА = AC. В точке начала эвольвенты её радиус кривизны равен нулю, ρA0 = 0.
3) Радиус кривизны эвольвенты в данной точке равен отрезку производящей прямой, заключённому между данной точкой эвольвенты и точкой касания производящей прямой с основной окружностью, ρА = AC. В точке начала эвольвенты её радиус кривизны равен нулю, ρA0 = 0.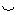 C0C.
C0C. длиной радиус-вектора Ry и углом θy. Радиус-вектор Ry определим из прямоугольного треугольника OAyCy:
длиной радиус-вектора Ry и углом θy. Радиус-вектор Ry определим из прямоугольного треугольника OAyCy:



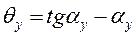 .
.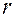 , в зацеплении двух колёс имеет индекс номера колеса):
, в зацеплении двух колёс имеет индекс номера колеса):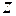 ;
; ,
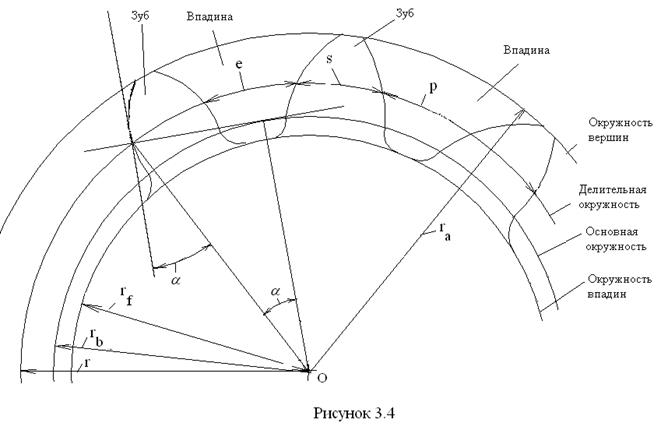
, – высота головки зуба, причём
– высота головки зуба, причём  . Множитель перед модулем называется коэффициентом высоты головки зуба и равен по величине 1, т. е.
. Множитель перед модулем называется коэффициентом высоты головки зуба и равен по величине 1, т. е.  .
. ,
, где
где  – высота ножки зуба, определяемая равенством
– высота ножки зуба, определяемая равенством  , второе слагаемое в скобках называется коэффициентом радиального зазора и имеет величину
, второе слагаемое в скобках называется коэффициентом радиального зазора и имеет величину  .
.















