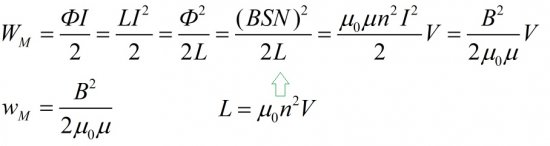Электромагнитные колебания и волны
Для колебательного контура предыдущей задачи написать уравнение (с числовыми коэффициентами) изменения со временем t энергии электрического поля Wэл, энергии магнитного поля Wм и полной энергии поля W. Найти энергию электрического поля, энергию магнитного поля и полную энергию поля в моменты времени Т/8, Т/4 и Т/2. Построить графики этих зависимостей в пределах одного периода.
Дано:
q = 2,5 мкКл = 2,5·10 -6 Кл
Решение:
Энергия электрического поля на обкладках конденсатора
Энергия магнитного поля в катушке индуктивности
Полная энергия в контуре
Закон изменения напряжения на обкладках конденсатора
Период колебаний находим по формуле Томсона
Циклическая частота связана с периодом соотношением
Уравнение колебания напряжения запишется в виде
Аналогично можно записать уравнение изменения заряда на обкладках конденсатора
Ток в контуре – первая производная от заряда по времени
Энергия катушки индуктивности
Энергия катушки индуктивности (W) — это энергия магнитного поля, порождаемого электрическим током I, текущим по проводу данной катушки. Главная характеристика катушки — ее индуктивность L, то есть способность создавать магнитное поле при похождении по ее проводу электрического тока. У каждой катушки индуктивность и форма свои, поэтому и магнитное поле для каждой катушки будет отличаться величиной и направлением, хотя ток может быть абсолютно одинаковым.
В зависимости от геометрии конкретной катушки, от магнитных свойств среды внутри и около нее, — создаваемое пропускаемым током магнитное поле в каждой рассматриваемой точке будет обладать определенной индукцией B, как и величина магнитного потока Ф — тоже будет определенной на каждой из рассматриваемых площадок S.
Если попытаться объяснить совсем просто, то индукция показывает интенсивность магнитного действия (связанного с силой Ампера), которое способно оказать данное магнитное поле на проводник с током, в это поле помещенный, а магнитный поток обозначает то, как распределена магнитная индукция по рассматриваемой поверхности. Таким образом, энергия магнитного поля катушки с током локализована не непосредственно в витках катушки, а в том объеме пространства, в котором существует магнитное поле, c током катушки связанное.
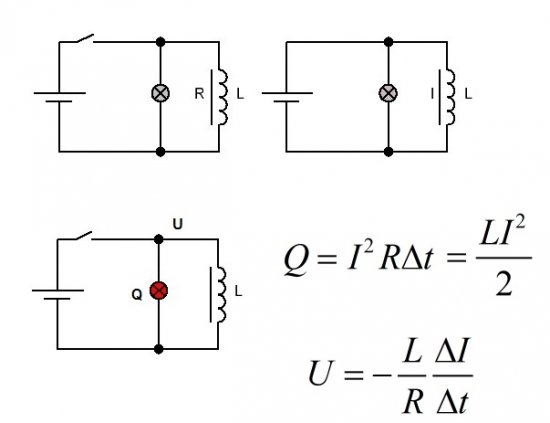
То, что магнитное поле катушки с током обладает реальной энергией, можно обнаружить экспериментально. Соберем схему, в которой параллельно катушке с железным сердечником подключим лампу накаливания. Подадим на катушку с лампочкой постоянное напряжение от источника питания. В цепи нагрузки тут же установится ток, он потечет через лампочку и через катушку. Ток через лампочку будет обратно пропорционален сопротивлению ее нити накала, а ток через катушку — обратно пропорционален сопротивлению провода, которым она намотана.
Ежели сейчас резко разомкнуть тумблер между источником питания и цепью нагрузки, то лампочка кратковременно но довольно заметно вспыхнет. Это значит, что когда мы отключили источник питания, ток из катушки устремился в лампу, а значит данный ток в катушке был, он имел вокруг себя магнитное поле, и в момент исчезновения магнитного поля в катушке возникла ЭДС.
Данная индуцированная ЭДС называется ЭДС самоиндукции, поскольку навелась она собственным магнитным полем катушки с током на саму эту катушку. Тепловое действие Q тока в данном случае можно выразить через произведение величин тока, который был установлен в катушке на момент размыкания тумблера, сопротивления R цепи (провода катушки и лампы) и продолжительности времени исчезновения тока t. Напряжение, которое возникло на сопротивлении цепи, можно выразить через индуктивность L, полное сопротивление цепи R, а также с учетом времени исчезновения тока dt.
Применим теперь выражение для энергии катушки W к частному случаю — к соленоиду с сердечником, обладающим определенной магнитной проницаемостью, отличной от магнитной проницаемости вакуума.
Для начала выразим магнитный поток Ф через площадь сечения S соленоида, количество витков N и магнитную индукцию B по всей его длине l. Распишем сначала индукцию B через ток витка I, число витков на единицу длины n, и магнитную проницаемость вакуума.
Подставим затем сюда объем соленоида V. Мы нашли формулу для магнитной энергии W, и имеем право взять отсюда величину w – объемную плотность магнитной энергии внутри соленоида.
Джеймс Клерк Максвелл в свое время показал, что выражение объемной плотности магнитной энергии справедливо не только для соленоидов, но и для магнитных полей вообще.
Видео:Урок 292. Энергия магнитного поляСкачать
Самоиндукция. Энергия магнитного поля
Самоиндукция – это значимый частный случай электромагнитной индукции, когда магнитный поток, изменяясь и вызывая ЭДС индукции, создается током в самом контуре.
В случае, когда ток рассматриваемого контура по каким-либо причинам изменен, то имеет место изменение и магнитного поля этого тока, а значит и собственного магнитного потока, проходящего через контур. В контуре создается ЭДС самоиндукции, создавая препятствие для изменений тока в контуре (по правилу Ленца).
Собственный магнитный поток Φ , который проходит через контур или катушку с током, является пропорциональным силе тока I : Φ = L I .
Коэффициент пропорциональности L в формуле Φ = L I есть коэффициент самоиндукции или индуктивность катушки. Единица индуктивности в С И носит название генри ( Г н ) . Индуктивность контура или катушки равна 1 Г н , когда при силе постоянного тока 1 А собственный поток составляет 1 В б : 1 Г н = 1 В б 1 А .
Видео:Энергия магнитного поляСкачать
Расчет индуктивности
Для наглядности произведем расчет индуктивности длинного соленоида, который имеет N витков, площадь сечения S и длину l . Соленоид – это цилиндрическая катушка индуктивности, у которой длина много больше диаметра. Магнитное поле соленоида задается формулой:
где I является обозначением тока в соленоиде, n = N e указывает число витков на единицу длины соленоида.
Магнитный поток внутри катушки соленоида, проходящий через все N витков, составляет:
Φ = B · S · N = μ 0 n 2 S l
Таким образом, индуктивность соленоида будет выражена формулой:
L = μ 0 n 2 S · l = μ 0 n 2 V ,
где V = S l – объем соленоида, содержащий магнитное поле.
Результат, который мы получили, не берет в расчет краевых эффектов, а значит он является приближенно верным лишь для катушек достаточной длины. Когда соленоид заполнен веществом, имеющим магнитную проницаемость μ , при заданном токе I индукция магнитного поля будет возрастать по модулю в μ раз, а значит и индуктивность катушки с сердечником тоже получит увеличение в μ раз:
L μ = μ · L = μ 0 · μ · n 2 · V .
ЭДС самоиндукции, которая возникает в катушке при постоянном значении индуктивности, в соответствии с законом Фарадея записывается в виде формулы:
δ и н д = δ L = — ∆ Φ ∆ t = — L ∆ I ∆ t .
ЭДС самоиндукции является прямо пропорциональной индуктивности катушки и скорости изменения силы тока в ней.
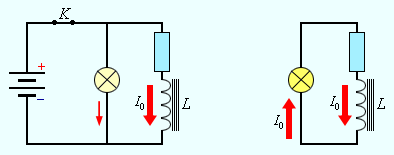
Магнитное поле выступает носителем энергии. Так же, как заряженный конденсатор обладает запасом электрической энергии, катушка, по виткам которой проходит ток, обладает запасом магнитной энергии. Включив электрическую лампу параллельно катушке с большой индуктивностью в электрическую цепь постоянного тока, при размыкании ключа будем наблюдать короткую вспышку лампы (рис. 1 . 21 . 1 ). Ток в цепи появится под влиянием ЭДС самоиндукции. Источником энергии, которая будет выделяться в этом процессе электрической цепью, будет служить магнитное поле катушки.
Рисунок 1 . 21 . 1 . Магнитная энергия катушки. В момент размыкания ключа K лампа ярко вспыхнет.
Закон сохранения энергии позволяет говорить, что вся энергия, составляющая запас катушки, будет выделена в виде джоулева тепла. Обозначим как R полное сопротивление цепи, тогда за время Δ t будет выделено количество теплоты Δ Q = I 2 · R · Δ t .
Ток в цепи составляет:
I = δ L R = — L R ∆ I ∆ t
Выражение для Δ Q можем записать так:
∆ Q = — L · I · ∆ I = — Φ ( I ) ∆ I
В данной записи Δ I 0 ; значение тока в цепи постепенно снижается от изначального I 0 до нуля. Полное количество теплоты, которое выделится в цепи, возможно получить, осуществив действие интегрирования в пределах от I 0 до 0 . Тогда получим:
Видео:Урок 287. Индуктивность контура (катушки). Явление самоиндукцииСкачать
Графический вывод формулы
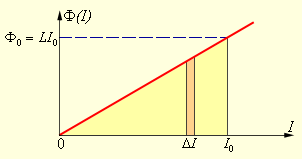
Существует возможность получить записанную формулу, используя графический метод. Для этого отобразим на графике зависимость магнитного потока Φ ( I ) от тока I (рис. 1 . 21 . 2 ). Полное количество выделившейся теплоты, которое равно изначальному запасу энергии магнитного поля, определится как площадь получившегося на рис. 1 . 21 . 2 треугольника:
Рисунок 1 . 21 . 2 . Вычисление энергии магнитного поля.
В итоге формула энергии W м магнитного поля катушки с индуктивностью L , создаваемого током I , будет записана в виде формулы:
W м = Φ I 2 = L I 2 2 = Φ 2 2 L
Используем выражение, которое мы получили, для энергии катушки к длинному соленоиду с магнитным сердечником. Применяя указанные выше формулы для коэффициента самоиндукции L μ соленоида и для магнитного поля B, создаваемого током I , получим запись:
W м = μ 0 · μ · n 2 · I 2 2 V = B 2 2 μ 0 · μ V
В этой формуле V является объемом соленоида. Полученное выражение демонстрирует нам, что магнитная энергия имеет локализацию не в витках катушки, по которым проходит ток, а распределена по всему объему, в котором возникло магнитное поле.
Объёмная плотность магнитной энергии – это физическая величина, которая равна энергии магнитного поля в единице объема: W м = B 2 2 μ · μ .
В свое время Максвелл продемонстрировал, что указанная формула (в нашем случае выведенная для длинного соленоида) верна для любых магнитных полей.
🔍 Видео
Магнитное поле соленоидаСкачать
Магнитное поле катушки с током. Электромагниты и их применение | Физика 8 класс #23 | ИнфоурокСкачать
Физика Какова индуктивность катушки, если при силе тока 3 А энергия магнитного поля катушки равнаСкачать
Индуктивность и ЭДС Самоиндукции. ЕГЭ Физика. Николай Ньютон. ТехноскулСкачать
Физика 11 класс (Урок№6 - Самоиндукция. Индуктивность.)Скачать
ДЛЯ ЧЕГО НУЖНА КАТУШКА ИНДУКТИВНОСТИ? #катушка #индуктивность #электроникаСкачать
Магнитное поле катушки с токомСкачать
Физика Энергия магнитного поля катушки индуктивностью 0,5 Гн равна 0,25 Дж Какова сила токаСкачать
Тема 30. Явление самоиндукции. Индуктивность. Энергия магнитного поля катушки с токомСкачать
Энергия МАГНИТНОГО поля | ЕГЭ Физика | Николай НьютонСкачать
ГИА-лаборатория. Взаимодействие магнита и катушкиСкачать
Урок 171 (осн). Магнитное поле витка и катушки с токомСкачать
Урок 281. Электромагнитная индукция. Магнитный поток. Правило ЛенцаСкачать
Физика - Магнитное полеСкачать
Рассмотрение темы: "Магнитное поле катушки"Скачать
Энергия магнитного поля катушки с током. Магнитный потокСкачать
Опыты по физике. Зависимость магнитного поля катушки от сердечникаСкачать
