Уравнение энергии для сжимаемого газа

Уравнения аэродинамики больших скоростей

Уравнение Бернулли для сжимаемого газа

Рассмотрим идеальное течение газа без вязкости. Кроме того, будем считать газ легким, следовательно, в нем будут отсутствовать массовые силы.

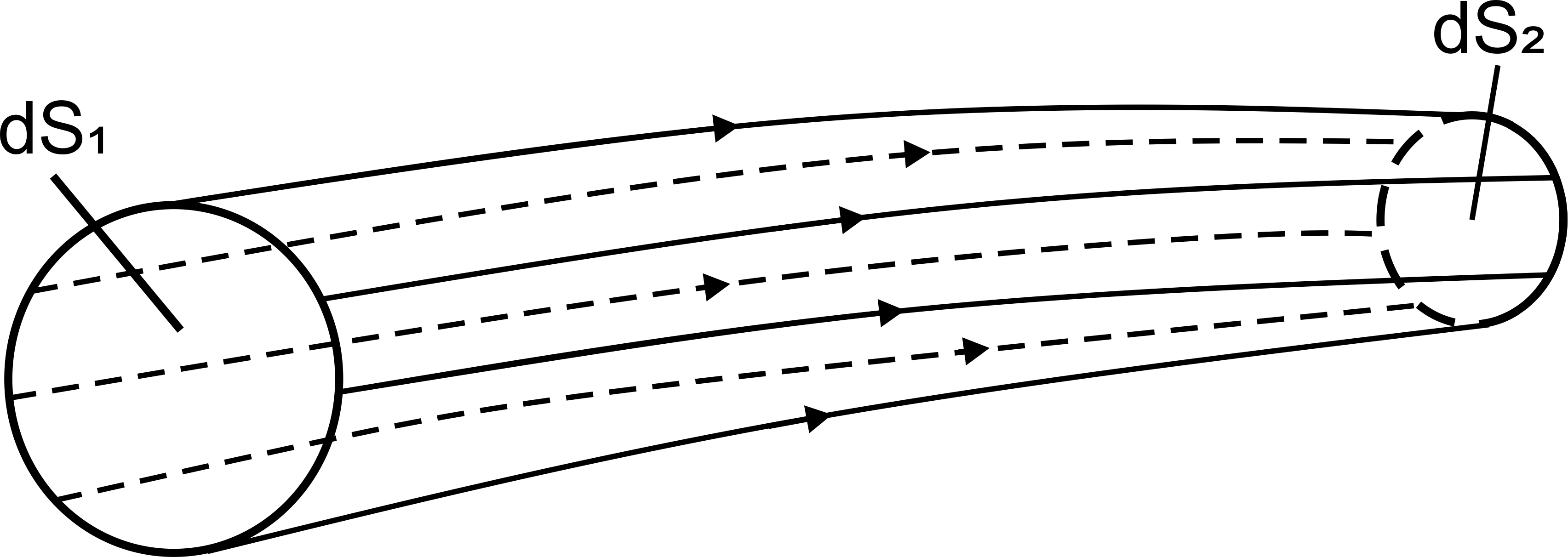
В потоке газа выделим элементарную струйку, ограниченную трубкой тока (рис.1.1). Здесь нужно вспомнить эти понятия основ аэродинамики и динамики полета.

Линия тока – кривая в потоке газа, в каждой точке которой вектор скорости в данный момент времени направлен по касательной.

Трубка тока – поверхность, образованная линиями тока, проведенными через все точки произвольного замкнутого контура площадью dS. Трубка тока считается непроницаемой для воздушных частиц.

Элементарная струйка – часть потока газа, ограниченная трубкой тока.

В связи с этим можно считать, что поток газа состоит из совокупности элементарных струек.

Рис.1.1 Элементарная струйка в потоке газа

Запишем для элементарной струйки 2-ой закон Ньютона

, (1.1)

который показывает, что произведение массы (газа) на ускорение равно сумме всех сил, действующих на тело (в данном случае – элементарную струйку). Проведем анализ данного уравнения (рис.1.2).

Рис.1.2 К выводу уравнения Бернулли для потока сжимаемого газа

В правой части уравнения (1.1) на элементарную струйку действуют силы давления по площадкам dS1, и dS2 , которые можно считать равными

.

По боковым поверхностям элементарной струйки силами давления пренебрегаем, так как они взаимно уравновешиваются. Силами трения (идеальный газ) и силами тяжести (легкий газ) также пренебрегаем.

или учитывая

,

.

Учитывая и сокращая на dS, имеем

. Перенося – dp в левую часть уравнения, и разделив обе части уравнения на , получим

. (1.2)

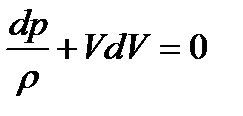
Внося скорость V под знак дифференциала, получим

. (1.3)

Уравнения (1.2) и (1.3) являются двумя формами записи уравнения Бернулли для газа в дифференциальном виде. Вспомним, что в основе уравнения Бернулли лежит закон сохранения энергии.

Современные магистральные ВС (Ту-204, Airbus A320 и др.) летают с достаточно большими скоростями. При числах Маха М>0,4 плотность газа начинает изменяться, и движение газа уже нельзя считать движением несжимаемой жидкости.

Чтобы найти конечные величины p и V или связь между этими параметрами в дифференциальном уравнении Бернулли, необходимо проинтегрировать уравнение (1.3)

. (1.4)

Для сжимаемого течения зависимость между p и r (без определения которой нельзя выполнить интегрирование) имеет вид

Для изоэнтропного (энтропия S не меняется), энергоизолированного (над газом не совершается работа) течения вместо показателя политропы n можно подставить k, и тогда интегрирование уравнения (1.4) можно выполнить.

В случае сжимаемого газа, когда плотность газа уже непостоянна, уравнение (1.4) после интегрирования преобразуется к виду

(1.5)

где k – постоянная изоэнтропы (адиабаты) и для воздуха равна 1,4.

Это и есть уравнение Бернулли для потока сжимаемого газа.

Величина в формуле (1.5) учитывает влияние сжимаемости. Для газа как несжимаемой жидкости при М

ПВД измеряют скоростной напор набегающего потока

. (1.7)

Здесь q – скоростной напор,

Dp – перепад давления или разность между полным и статическим давлением,

r – плотность воздуха на данной высоте,

V – скорость воздушного потока.

Однако указатель скорости измеряет не саму скорость, а скоростной напор . Поскольку при изменении высоты и скорости существенно изменяется плотность r, что происходит при полете магистральных ВС, то при измерении скорости полета возникают погрешности.

Воздушная (истинная) скорость полета V не совпадает с той скоростью, которую показывает прибор, т.к. на ПВД оказывает влияние создаваемые самолетом возмущения, а также сжимаемость воздуха. Кроме того, величина воздушной скорости зависит от инструментальной и других поправок.

Градуировка приборов для измерения скорости соответствует лишь полету у земли, когда Н = 0, а (или 1,225 ). При наборе высоты плотность падает и r

Индикаторная скорость в аэродинамике – это идеальная скорость, которую показывает прибор с учетом всех поправок.

Видео:Уравнение состояния идеального газа. 10 класс.Скачать

Термодинамические основы сжатия газов

Видео:Физика 10 класс (Урок№20 - Уравнение состояния идеального газа. Газовые законы.)Скачать

Уравнение состояния газа

В теории компрессорных машин, работающих в условиях, когда можно пренебречь межмолекулярными силами и размерами молекул, используется уравнение состояния идеального газа.

При сжатии воздуха и его составляющих (азот, кислород, аргон, водород, гелий и др.) в области давлений до 10 МПа и температур более 273 К применение уравнения дает погрешность не более 2%.

При более высоких давлениях сжатия сказывается объем молекул газа и влияние силы межмолекулярного притяжения. Многоатомные газы и пары при давлениях и температурах, близких к критическим, не следуют уравнению состояния идеального газа. В этом случае газ рассматривается как реальный.

Объем реального газа при низких давлениях и температурах из-за. взаимного притяжения молекул меньше, чем у идеального газа, а при высоких давлениях больше, чем у идеального при влиянии собственного объема молекул. Избыточный объем газа, учитывающий объем молекул и влияние сил межмолекулярного притяжения, равен разности при одинаковых условиях.

Значения коэффициента и показателя отклонения сжимаемости Р в зависимости от давления и температуры для ряда газов приведены на рис 2.1 и в приложении П.З.

Для газовой смеси, если ее компоненты в процессе сжатия не конденсируются и не вступают друг с другом в химическую реакцию, справедливы уравнения состояния идеального и реального газов, приведенные выше. Использование этих уравнений возможно, если известны значения газовой постоянной смеси Rcm и коэффициента сжимаемости смеси 5см.

Использование правила аддитивности для определения коэффициента ξсм дает надежные результаты только в тех случаях, когда значения коэффициентов сжимаемости отдельных газов, составляющих смесь, близки друг к другу. Если же они существенно отличаются друг от друга, сумма парциальных объемов отдельных газов, составляющих газовую смесь, будет отличаться от объема смеси и поэтому значение, найденное по (2.10), будет неточным.

Для более точного определения может быть рекомендован метод, основанный на использовании закона соответственных состояний.

Видео:Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать

Процессы сжатия в компрессорных машинах

Процессы сжатия газа в компрессорных машинах обычно рассматриваются в системах Т, s- и р, υ-координат.

Термодинамический рабочий процесс компрессора протекает по политропе и описывается уравнением р/рη — const.

Для начальных и конечных параметров сжимаемого газа в изо-энтропном процессе (рис. 2.2) повышение температуры пропорционально увеличению давления и зависит от показателя k:

В теории компрессорных машин рассматриваются так называемые эталонные процессы: для машин без внутреннего охлаждения (лопастной компрессор)—адиабатный процесс; для машин с внутренним охлаждением (поршневой компрессор, многоступенчатый компрессор) — изотермический процесс.

Действительные рабочие процессы характеризуются наличием теплообмена с окружающей средой, а также наличием внутреннего теплопритока в результате работы сил трения в процессе сжатия газа.

Пренебрегая теплообменом с окружающей средой и работой сил трения в ступени центробежного компрессора, получаем эталонный процесс сжатия — изоэнтропное сжатие (n = k) (адиабатное сжатие без учета работы сил трения). Рабочим процессом ступени центробежного компрессора считается по-литропное сжатие с учетом работы сил трения (n>k)y если пренебречь теплообменом с окружающей средой. Эталонным процессом охлаждаемых машин считается изотермический, а рабочим процессом — политропный, проходящий с охлаждением (рис. 2.3).

Изотермический процесс сжатия газа в компрессоре изображен на рис. 2.3 горизонтальной линией при Т = const pv — const.

Видео:Урок 145. Идеальный газ. Основное ур-ние МКТ ид. газа - 1Скачать

Уравнения сохранения энергии в компрессорных машинах

Энергия, сообщенная сжимаемому газу в компрессоре, расходуется на изменение энтальпии газа, кинетической и потенциальной энергии его и на покрытие тепловых потерь в окружающую среду. Пренебрегая изменением потенциальной энергии положения, дифференциальное уравнение энергии потока газа, отнесенное к 1 Кг массы газа, Дж/кг, можно записать, где dLi — элементарная энергия, сообщенная газу; dh — изменение энтальпии газа; d(c2/2) — изменение кинетической энергии газа; dqo — отведенное от газа количество теплоты. Интегрируя от входа до выхода компрессора получаем, что

Для неохлаждаемой ступени лопастного компрессора, если пренебречь теплообменом с окружающей средой,
где Li — внутренняя удельная работа лопастного компрессора. Энергия газового потока характеризуется единым параметром, называемым полная энтальпия:
Полная энтальпия h* и полная температура T* соответствуют так называемому полному давлению р*, которое имел бы газ при преобразованной без потерь кинетической энергии (адиабатный поток).

Движение реального (вязкого) газа сопровождается внутренними потерями энергии на трение и вихреобразование в рабочих органах компрессора. Энергия, израсходованная на трение и вихреобразование, Lr полностью превращается в тепловую энергию qr и передается потоку газа.

Уравнение сохранения энергии (первый закон термодинамики) имеет вид
dq = du + pdv,
где dq — элементарное количество теплоты, сообщенное газу; du — элементарное изменение внутренней энергии газа; pdv — элементарная внешняя работа газового процесса.

Известно, что для идеального газа
dh = du + d(pv) = du + pdv + vdp или
du = dq — pdv — vdp.

Подставим значение du в уравнение:
dq = dh — vdp,
где vdp — элементарная работа сжатия и перемещения газа.

В общем случае величина dq в компрессоре равна
dq = dqr — dq0
где dqr = dLr — элементарное количество теплоты, сообщенной газу вследствие потерь на трение и вихреобразование; dq0 — элементарное количество теплоты, отведенной от. газа. Из уравнений следует
vdp + dLr = dh + dq0.

Рассмотренные уравнения энергии используются в теории и расчетах компрессорных машин.

Видео:Уравнение состояния идеального газа | Физика 10 класс #33 | ИнфоурокСкачать

Охлаждение газа в компрессоре

Охлаждение газа в компрессоре уменьшает работу сжатия. При этом температура сжимаемого газа уменьшается до допустимых значений. Охлаждение в процессе сжатия обычно применяется при относительно высокой степени сжатия на ступень (поршневые компрессоры) или при большом значении показателя адиабаты (газы с большой молекулярной массой).

В компрессоростроении применяются следующие способы охлаждения сжимаемого газа: внутреннее, внешнее, комбинированное и предварительное, а также охлаждение путем впрыска охлаждающей среды в проточную часть машины.

Внутреннее охлаждение осуществляется непосредственно в процессе сжатия газа путем охлаждения стенок рабочих органов компрессора и обычно применяется в объемных машинах (поршневые, винтовые, ротационные и др. компрессоры) . Охлаждаемая среда — обычно вода или окружающий воздух.

В лопастных компрессорах внутреннее охлаждение применяется редко по ряду причин: увеличиваются размеры компрессора и компрессорной установки, увеличиваются гидравлические потери в неподвижных элементах рабочих органов из-за увеличения поверхности охлаждения, возможна конденсация влаги, имеющейся в сжимаемом газе и др.

Внешнее охлаждение газа осуществляется в межступенных холодильниках, расположенных вне проточной части компрессора. Сжатый газ охлаждается во внешнем холодильнике при некотором снижении давления из-за гидравлических потерь в холодильнике почти до первоначальной температуры.

На рис. 1.10 показана схема трехступенчатого поршневого компрессора с двумя промежуточными (межступенчатыми холодильниками). На рис. 2.5 показана Т, s-диаграмма рабочего процесса сжатия вышеуказанного компрессора при условии, что газ сжимается в отдельных ступенях по политропе п > k и охлаждается почти до первоначальной температуры в каждой ступени без потерь давления в холодильниках, т. е. при р = const. Заштрихованная площадь диаграмм соответствует уменьшению подводимой энергии на сжатие газа при межступенном охлаждении. Имеющаяся в сжимаемом газе влага конденсируется в межступенных холодильниках и удаляется.

Рис. 2.5. Т, s-диаграмма трехсекционного лопастного компрессора с промежуточным охлаждением

Комбинированное охлаждение предусматривает применение одновременно внутреннего и внешнего охлаждения (поршневые, винтовые и другие компрессоры объемного типа). На рис. 2.6 показана Т, s-диаграмма различных процессов сжатия в компрессоре.

Предварительное охлаждение целесообразно применять, когда имеется существенная разница между температурой всасываемого газа и охлаждающей водой. Установленный перед компрессором холодильник, снижая температуру поступающего газа, увеличивает плотность, массовый расход и потребляемую мощность. С энергетической точки зрения предварительное охлаждение нерационально, так как экономия работы сжатия за счет охлаждения невелика из-за повышения потребляемой мощности при увеличении плотности газа.

Применение промежуточных холодильников увеличивает металлоемкость и усложняет конструкцию машины, повышает ее себестоимость на 20—30 % по сравнению с неох-лаждаемыми компрессорами. Использование охлаждающей воды увеличивает эксплуатационные затраты. Применение охлаждения газа должно основываться на результатах технико-экономических расчетов. Считается возможным изготовлять неохлаждаемые компрессоры стационарного типа с 8 2, а при сжатии пропана или фреона-12 (k = 1,14) при е > 10. При дефиците воды используется воздушное охлаждение.

Теплоту, отводимую от компрессоров, можно иногда использовать в качестве вторичных энергетических ресурсов для обогрева теплиц, зданий и др.

Охлаждение впрыском жидкости в поток перекачиваемого газа можно применять, если впрыскиваемая жидкость существенно не влияет на свойства перекачиваемых газов (вода — воздух; жидкий аммиак — аммиак; слабый раствор азотной кислоты — нитрозный газ). Охлаждение газа происходит за счет теплоты испарения жидкости. Жидкость от постороннего источника через распыливающие форсунки впрыскивается непосредственно в проточную часть компрессора. Например, при впрыскивании 1% по массе воды температура сжимаемого воздуха снижается примерно на 25°С.

При применении предварительного охлаждения газа обычно приходится использовать специальную холодильную установку. Так, например, на компрессорных станциях магистральных северных газопроводов газ предварительно охлаждается во избежание подтаивания грунта в зоне трубопровода.

Видео:Галилео. Эксперимент. Закон БернуллиСкачать

Влияние начального давления на работу сжатия компрессора

Давление всасывания воздушного компрессора зависит от барометрического давления, определяемого высотой установки компрессора над уровнем моря. Для дожимающих и циркуляционных компрессоров давление всасывания может изменяться в широких пределах в соответствии с требованиями

технологических процессов. Поэтому необходимо определить, как зависит работа, затрачиваемая на сжатие газа в ступени компрессора, от давления всасывания.

Для определения отношения давления, соответствующего максимуму работы, продифференцируем зависимость.

Видео:Идеальный газ. Основное уравнение молекулярно-кинетической теории газов. 10 класс.Скачать

Применение тепловых диаграмм при расчете поршневого компрессора

Выполнение теплового расчета поршневого компрессора с использованием тепловых s, Т- и s, ft-диаграмм позволяет существенно упростить расчет. На s, 7-диаграмму (рис. 2.8) наносятся изобары (р = — const), а также линии постоянной энтальпии (h — const).

Удельная энтальпия идеального газа зависит только от температуры. Удельная энтальпия реального газа зависит от температуры и давления, поэтому линии постоянной энтальпии представляют собой кривые, которые с уменьшением энтропии в области относительно низких давлений.

Линия, разграничивающая эти области и проходящая через точку К, соответствующую состоянию газа, при котором ε == 1, называется кривой инверсии.

Параметры реального газа на этой кривой подчиняются уравнению состояния идеального газа. Область диаграмм, расположенная справа от кривой инверсии, соответствует состояниям, при которых дросселирование газа от давления Pi до давления р2 приводит к снижению температуры на A7 = 7i — Т2. Для состояний газа, охватываемых областью диаграмм слева от кривой инверсии, характерно повышение температуры при дросселировании.

На диаграмме имеется граничная кривая, проходящая через точку К. и соответствующая критическим параметрам состояния газа; она разграничивает диаграмму на две области. Над кривой находится область сухого пара или газа; под кривой — область влажного пара или газа.

Ha s, Т-диаграмме q изображается площадью под линией процесса, ограниченной двумя ординатами. Энтропия газа возрастает, если процесс изменения его состояния осуществляется с подводом теплоты, и убывает, если этот процесс происходит с отводом теплоты. В случае же, еслц процесс изменения состояния газа идет без теплообмена (и без потерь), энтропия газа не изменяется.

На диаграмме показаны изотермический (7 = const линия 1-2) у изоэнтропный (n-const линия 1-2′) и политропный (линия 1-2″ и 1-2″) процессы сжатия идеального газа от давления р1 до давления р2. Количество теплоты, отводимой от газа в изотермическом процессе, выражается площадью диаграммы под линией 1-2.

Изоэнтропический процесс характеризуется отсутствием теплообмена и потерь, вследствие чего для этого процесса s = const. Что касается политропного процесса, то в случае, если показатель политропы п меньше показателя изоэнтро-пы, процесс происходит с отводом теплоты и кривая процесса 1-2″ располагается левее линии изоэнтропического процесса 1-2′.

Количество подводимой к 1 кг газа теплоты изображается площадью под кривой 1-2″ (+q), а от-водимой — площадью под кривой 1-2″ (—q). s, Г-диаграмма позволяет найти и количество теплоты, отводимой от 1 кг газа в холодильнике.

При условии охлаждения газа от температуры нагнетания Т2 до температуры всасывания Т1 количество теплоты равно площади диаграммы под отрезком изобары р2» соответствующим изменению температуры газа от Т2 до Т1.

Суммарное удельное количество теплоты qc, отводимое от идеального газа в цилиндре и холодильнике при охлаждении газа до температуры Ти равно удельной работе цикла
qс = l = q1 + q2,
где q2 — удельное количество теплоты, подводимое к газу (или отводимое от него) в цилиндре; q1 — удельное количество теплоты, отводимое от газа в холодильнике.

В изотермическом цикле q1 = О и l = q2. В изоэнтропическом цикле q2 = 0 и l = q1. В политропном цикле l = q2 + q1 причем q2 может быть положительным в зависимости от» того, подводится теплота к газу в цилиндре в процессе сжатия или отводится от него.

При сжатии реального газа связь между количеством теплоты, отведенной от газа в цилиндре и холодильнике, и работой 1, затраченной на осуществление цикла в ступени, выражается зависимостью
qc = l — (h» — h1),
где h1 — энтальпия всасываемого в ступень газа; h» — энтальпия газа, выходящего из холодильника.

Для реального газа даже если температура газа, выходящего из холодильника T», равна температуре всасываемого в ступень газа Т1. Работа и теплота в s, T-диаграмме при изотермическом и изоэнтропном сжатии реального газа показаны на рис. 2.9.

Из рисунка видно, что в зависимости от того, какой знак имеет разность h» — h1 работа, затрачиваемая в изотермическом и изоэнтропном сжатии реального газа, может превышать количество отводимой теплоты или быть меньше. Аналогично и при политропном сжатии реального газа.

В общем случае если сжатие осуществляется при состояниях газа, соответствующих области, расположенной на s, Г-диаграмме левее и выше кривой инверсии (высокие давления и температуры газа), затраченная работа превышаем количество теплоты qc, отводимое от газа в цилиндре и холодильнике. Если сжатие осуществляется при состояниях газа, соответствующих области, расположенной на s, Г-диаграмме правее кривой инверсии (низкие давления и температуры газа), затраченная работа меньше количества теплоты — qc.

В s, T-диаграмме (рис. 2.10) по горизонтальной оси откладывается удельная энтропия s и по вертикальной оси — удельная энтальпия Л. На диаграмму нанесены изобары р = const и изотермы Т = const, s, h-диаграмма применяется для определения удельной работы в изо энт р опическом. реального газа ta и удельного количества теплоты q1 отводимого от реального газа в холодильнике.

Видео:Физика. МКТ: Уравнение Менделеева-Клапейрона для идеального газа. Центр онлайн-обучения «Фоксфорд»Скачать

Закон Бернулли для чайников и учёных

Предисловием можно считать «За что физики не любят математиков»: http://proza.ru/2015/11/16/160

а началом — «О прилипании предметов к телу человека»: http://proza.ru/2015/03/06/306

«Наука должна быть весёлая, увлекательная и простая. Таковыми же должны быть и учёные» (П.Л. Капица). и преподаватели. Но более всего наука должна быть честная. И «Ни один человек не должен покидать стены наших университетов без понимания того, как мало он знает» (Роберт Оппенгеймер). и как мало знают учёные. А чтобы так оно и было, нужно срезать профессора математической лженауки на первой же лекции. И прежним занудой он уже не будет. Знаю, что говорю, и привожу очередной пример.

Курс лекций по гидродинамике и аэродинамике начинается с закона Бернулли. Первый вопрос профессору на засыпку: «Что именно измеряют или показывают три трубчатых манометра на картинке вверху — давление в потоках или давление потоков?».

Правильный ответ: неподвижные поверхностные манометры на картинке вверху показывают давление потоков, так как для измерения давления в потоках нужны такие манометры или датчики давления, которые находились бы внутри потоков и двигались вместе с ними. Давление внутри потоков, знаете ли, почти всегда статично. Но таких мобильных манометров, которые могли бы быть неподвижными относительно ламинарных потоков, нет в опытах к теме «Закон Бернулли». Однако вывод сделан такой, словно они есть, словно давление внутри потоков уже измерено. «Для физика должно существовать только то, что измерено» (Нильс Бор). а не то, что можно подумать, придумать, недодумать и сосчитать. Сосчитать то, чего нет, может каждый.

С маленькой лжи, как правило, начинается ложь большая. «Ложь большая» — это теория. Правильных теорий не бывает, поэтому «Никаким количеством экспериментов нельзя доказать теорию, но достаточно одного эксперимента, чтобы её опровергнуть» (А.Э.). Вся научная гидродинамика и аэродинамика опровергаются опытами по измерению давления в потоках.

Профессор, ау-у. Вы нас слышите. В опытах к теме «Закон Бернулли» нет соответствующих выводам измерений. Вы врёте по причине того, что ни один математик не отличает «давление потока» от «давление в потоке». Доказательства — картинки из учебников и глупые формулки под ними.

Так как давление в потоках у теоретиков не измерено, профессору опыт на картинке вверху говорит одно, а нам — другое: «Давление потока на параллельную потоку поверхность всегда тем меньше давления в самом потоке, чем больше скорость потока; а давление потока на поперечную или наклонную поверхность всегда тем больше давления в потоке, чем больше скорость самого потока». И чем наш вывод хуже.

А тем-то он и хуже, что никакой научности и сложности для понимания в нём нет. К тому же, давление потока на поперечную поверхность или «скоростной напор» измеряется с помощью Г-образной «трубки Пито», вставляемой в поток загнутым концом навстречу потоку. Отсюда: давление в самом потоке примерно равно среднему арифметическому от показаний «трубки Пито» и «трубки у Бернулли». Более того, в ньютоновской механике уменьшение силы давления на параллельную потоку или телу поверхность с увеличением скорости потока или тела и одновременное увеличение давления потока или тела на поперечную поверхность можно объяснить простым векторным разложением силы давления потока или тела. Чем больше скорость автомобиля, тем меньше его вес и давление на дорожное полотно; чем больше скорость потока, тем меньше его давление на стенки трубы. Пусть пока будет так.

Конечно, наши выводы профессору будут сильно не по нутру. Но если он будет ещё в состоянии что-то говорить и продолжит настаивать на том, что «С увеличением скорости потока давление внутри потока уменьшается», то срежем его вторым вопросом: «Почему причина и следствие в формулировке общепризнанного закона Бернулли переставлены местами?».

Действительно, так сформулировать общий закон потоков мог только теоретик с математическим складом ума, для которого «Что полумёртвый равен полуживому, что полуживой равен полумёртвому, а «полу-» вообще можно сократить». А для физика и инженера давление всегда первично, а сам поток и его скорость — это всегда лишь следствие. Инженер так никогда не скажет: мол, чем больше скорость потока, тем меньше давление в нём. Для него это утверждение является противоречием здравому смыслу, то есть оксюмороном: дескать, чем выше фонтан, тем меньше давление в трубе. А как скажет инженер?

Инженер скажет: «Поток можно создать двумя противоположными, но равнозначными способами — локальным (или местным) повышением давления и локальным понижением его, потому что любой поток всегда движется в сторону меньшего давления. Это главный закон потоков или аксиома потоков, поэтому давление в потоке всегда стремится к выравниванию с внешним давлением и к уменьшению. При этом чем значительнее перепад и падение давления мы имеем или создаём, тем больше будет и скорость потока».

Можно короче: «Чем больше падение давления в потоке или на данном участке трубы, тем больше здесь и скорость самого потока». И это будет тривиальный закон потоков, у которого уже есть все пять обязательных признаков новой истины: простота, ясность, универсальность, «предсказательная сила» и антинаучность. Опровергнуть этот закон сможет только тот, кто создаст поток жидкости или газа, движущийся из области пониженного давления в область повышенного давления, то есть против действия превосходящих сил давления и упругости. Шутка.

«Тривиальный» — значит, яснее и проще некуда; значит, это закон-аксиома. К примеру, очень значительный перепад давления мы имеем сразу за камерой сгорания ракеты (примерно 250 атмосфер), и только поэтому скорость частиц реактивной струи, как говорят, достигает 3-х км/с. Вопрос профессору: «Что толкает ракету — закон сохранения импульса или асимметричное давление непрерывного взрыва в асимметричной камере сгорания?». Если скажет, что закон, перед вами математик. Стреляйтесь сразу, ибо ничто физическое и реально существующее вы ему объяснить уже не сможете (никто не сможет). «Математики похожи на французов: что бы вы ни сказали, они всё переведут на свой собственный язык. Получится нечто противоположное» (Гёте).

Если скоростной поток жидкости инженеры создают в длинной горизонтальной трубе постоянного сечения, то тут будет так: чем большее давление нагнетается в трубе, тем больше будет скорость потока в трубе при постепенном падении давления в потоке к концу трубы, то есть к расширителю потока. Всё проще простого: наибольшее давление в потоке будет в начале трубы, а наименьшее — в конце, при этом скорость несжимаемого потока будет одинаковой и там, и тут. Постепенное падение давления в потоке будет происходить по причине уменьшения массы (как меры инерции) и веса прокачиваемых жидкостей или газов на различных участках протяжённой трубы по мере приближения к концу трубы.

Любой пожарник скажет, что так оно и есть, ведь давление воды и в вертикальном потоке тоже убывает по мере приближения к концу пожарного рукава по причине уменьшения веса воды в столбе воды. А физик вспомнит ещё и про третий закон Ньютона — «Действие не может быть больше противодействия». «Действие» — это в данном случае сила нагнетаемого давления; а «противодействие» — это масса и вес потока плюс атмосферное давление на противоположном конце трубы. Противодействие уменьшается к концу трубы, и давление в потоке стремится к атмосферному.

Итак, давление в потоке жидкости на разных участках трубопровода всегда различное, а скорость потока всегда одна и та же; давление в жидкости может уменьшаться, а скорость потока при этом может сохраняться. Где тут закон Бернулли для давления в потоках. Законы Ньютона, да, мал-мало есть, а Бернулли нет и близко. Но для математиков закон есть закон, поэтому давление в скоростном потоке у них всегда низкое по всей длине трубопровода. Трубопровод разорвало. и никто не знает почему. А виноват Даниил Бернулли. Но «Кто ж его посадит, он же — па-мят-ник!».

Инженер-аэродинамист сформулирует свой закон потоков примерно так: «Давление потока на параллельную или отрицательно наклонную поверхность всегда тем меньше давления в самом потоке, чем больше скорость потока или поверхности (верхней поверхности крыла); а давление потока на поперечную или положительно наклонную поверхность всегда тем больше давления в самом потоке, чем больше скорость потока или поверхности (нижней поверхности атакующего крыла)». И это будет качественный закон взаимодействия потоков с поверхностями, так как в каждом конкретном случае величина давления потока на поверхность зависит не только от скорости потока, но и от физических свойств потока и поверхности, поэтому она не вычисляется, а только измеряется. Следовательно, математикам и в аэродинамике делать особо нечего.

Так что, два математических закона Бернулли мы отменили. Зато, теперь имеем два основных физических закона потоков — тривиальный и качественный. И всё в этих законах понятно, и всё работает. Профессор «падсталом». Но добьём его математическую лженауку.

Действие этих двух законов во многих опытах и явлениях складывается или накладывается, поэтому наблюдаемый результат нельзя объяснять действием только какого-то одного закона. Но объединённого закона Бернулли или третьего математического закона потоков никогда не было, поэтому как определить «личную долю» каждого закона в результате того или иного опыта к теме «Закон Бернулли» не знает ни один математик. но знает каждый инженер. Он просто измеряет с помощью манометров и динамометров давление в потоке и давление потока при различной скорости потока, а потом лишь сравнивает результаты измерений. и никаких теорий потоков для него словно не существует. Действительно, зачем вычислять, если можно измерить.

Сосчитать то, чего нет, может каждый. и превратить теоретическую физику в то, чего не может быть, чего уже никто не понимает, — тоже. Математические законы Бернулли — это лишь частный случай того, чего не может быть. Впрочем, математик всегда начинает считать, не спев подумать. Сейчас мы в этом снова убедимся.

Если подуть между двумя бумажными листами, подвешенными параллельно друг другу, листы сблизятся и почти сомкнутся. Можно подуть, а можно, наоборот, прососать пылесосом воздух между листами — результат тот же.

Математик Леонард Эйлер назвал этот опыт своего друга Даниила Бернулли «Великим парадоксом», ведь в первом случае листы должны были раздвинуться расширяющимся сжатым потоком. Сам назвал — сам и объяснил. через постоянство суммы потенциальной и кинетической или полной энергии замкнутой системы. Объяснил опять же уменьшение давления в потоке с увеличением скорости потока, а не уменьшение давления потока на листы, то есть объяснил совсем не то, что надо было объяснять. И объяснил опять же математикам, а не инженерам. Инженеры твёрдо знают: давление в потоке выдуваемого из лёгких воздуха не может быть меньше атмосферного давления. А вот давление выдуваемого потока на параллельные листы может быть меньше атмосферного, поэтому листы и смыкаются. Так мы о том и говорим. Кстати, ещё вопросец на засыпку: «С какого места в опытах к теме «Закон Бернулли» начинается «замкнутая система?». Профессор, ау-у. (Правильный ответ: «С головы».)

Качественный закон потоков гласит: «Давление потока на параллельную ему поверхность всегда тем меньше давления в самом потоке, чем больше скорость этого потока и чем больше хаос в движении частиц пограничного слоя потока». Можно короче: «Давление потока на параллельную поверхность всегда тем меньше, чем больше хаос в движении частиц потока».

В этой формулировке уже появилась физическая, а не математическая или теоретическая причина уменьшения давления потока на поверхность — это хаос или беспорядок в движении пограничных частиц потока. Вот почему на результат действия первого или тривиального закона потоков всегда накладывается действие второго или качественного закона, если мы рассматриваем взаимодействие потоков со стенками трубы, например, или с подвешенными листами. Однако давление внутри потока по-прежнему не измерено, а хаос в пограничном слое потока увидеть нельзя… Нет, уже всё можно. Человек, знаете ли, видит мир не глазами и слышит его не ушами.

В гидродинамике давление всегда первично, а скорость потока вторична; в аэродинамике скорость крыла всегда первична, а давление неподвижной атмосферы на него всегда вторично. Плоское крыло самолёта или птицы не изменяет давление в неподвижной атмосфере, а изменяется с увеличением скорости и угла атаки лишь взаимодействие быстрого крыла с атмосферой. Но в наших рассуждениях крыло чаще всего неподвижно, а это атмосфера «набегает» на крыло, словно всё происходит в аэродинамической трубе или в статическом (стационарном) потоке. Просто так нам удобнее рассуждать и объяснять.

У инженеров всё, что летает, делает это по причине совсем небольшой положительной разницы или асимметрии атмосферного давления на крыло. Появление подъёмной силы как раз и обусловлено качественным законом потоков: «Давление атмосферного потока на верхнюю отрицательно наклонную поверхность быстрого крыла тем меньше давления в самой атмосфере, чем больше хаос и разрежение частиц воздуха над ней; а давление потока на нижнюю положительно наклонную поверхность крыла тем больше атмосферного давления, чем больше скорость крыла, его угол наклона или атаки и деформация или уплотнение упругого воздуха под быстрым крылом». Как диагональ делит прямоугольник на два равных треугольника, так и плоское атакующее крыло делит набегающий поток на две самостоятельные и равнозначные причины возникновения подъёмной силы.

Вспомним, атмосферное давление на уровне моря равно 1,0033 кг/см2. Это очень большая сила, которая давит на неподвижное плоское крыло совершенно одинаково и сверху, и снизу. Если атмосферное давление со стороны одной из поверхностей крыла убрать, то со стороны противоположной поверхности тут же возникнет сила равная 10033 кг/м2. Да, 10 тонн на каждый квадратный метр крыла! И что мы имеем: орёл весом 4 кг, имея площадь «несущих поверхностей» как раз 1м2, почти неподвижно парит в вышине при положительной разнице атмосферных давлений на его крылья всего 0,04% от теоретически возможного 1 кг/см2; АН-2 («кукурузник») летает горизонтально на разности 0,4% атмосферного давления; а скоростному современному пассажирскому авиалайнеру для горизонтального полёта достаточно и 5% от 1 кг/см2 или 50 г/см2.

Как инженеры это узнали? Они применили принцип пропорциональности Леонардо да Винчи и разделили вес орла или летательного аппарата на площадь его несущих поверхностей. Вот и всё. А у математиков всё, что летает, летать не может по причине крайне не достаточной (в 6 раз меньше веса самолёта или божьей твари) подъёмной силы, вычисленной ими по самым надёжным математическим законам ньютоновской механики. Можете посмотреть по запросу «Парадокс шмеля», как математики из NASA и британские учёные вычисляли подъёмную силу. Ужас! Знание математической физики сделало их ещё глупее, чем когда они родились. И вообще, математик, считающий себя физиком, — это ноль в квадрате. Считать, что подъёмная сила крыла есть результат сопротивления воздушной среды его движению, в наше время может только профессор математики, а не физики. Читайте по запросу «О математическом идеализме в физике» (это не только мои статьи).

Идеальный или самый эффективный аэродинамический профиль – это «беспрофиль», то есть плоское, как лезвие безопасной бритвы, крыло. И это для передовых инженеров уже аксиома или «новая аэродинамика», а Природа это знала ещё со времён первых летающих насекомых и птеродактилей. Так вот, асимметричное атмосферное давление на совершенно плоское крыло возникает и при его нулевом угле наклона к вектору движения набегающего атмосферного потока, если верхняя поверхность крыла испещрена микроскопическими неровностями, а нижняя – максимально гладкая. В воде «эффект хаоса над крылом» проявляется ещё значительно сильнее.

Это утверждение доказано самой эволюцией живой природы и передовой практикой авиастроения. Смотрим на расправленное крыло любой птицы: сверху оно бархатистое и может играть всеми цветами радуги, что физику говорит о дисперсии света на мельчайших неровностях на поверхности, а снизу – всегда очень плотное, гладкое и со стальным отливом. Смотрим на современный пассажирский «Боинг»: сверху он словно матовый, а снизу – зеркально гладкий. И пусть та положительная разница в атмосферном давлении на крыло, которая возникает только по причине различного качества покрытия его аэродинамических поверхностей, будет и недостаточной для полёта, но именно она и позволит самолёту или птице лететь горизонтально с меньшим углом атаки, то есть с меньшим лобовым сопротивлением, экономя топливо и силы.

Инженеры «Боинга» говорят, что уже экономят на «эффекте хаоса над крылом» до 7-ми процентов топлива, а это огромные деньги. Смотрите фотографии «Боингов» и читайте по запросу «Аэродинамика Боинг». А наши дурни из Сколково одной краской покрывают весь Боинг. Смотрите по запросу «Красим Боинг». Кожа акулы тоже только кажется гладкой, а на ощупь она сравнима с наждачной бумагой. Шершавая кожа способствует образованию хаоса в пограничном слое воды, что ещё больше уменьшает её давление на быструю акулу. И таких примеров «мильён».

«Если ты не можешь объяснить что-либо просто — значит, ты сам этого не понимаешь» (Эйнштейн). или говоришь о том, чего нет, ибо познанное всегда проще непознанного. «Вашу теорию относительности не понимает никто в мире, но Вы всё-таки стали великим человеком» (Чаплин). «Человек, на исправление ошибок которого потребовалось целое десятилетие, — это действительно человек» (Оппенгеймер). Эйнштейн очень много сделал для любителей огромных и сверхмалых чисел и всевозможных формул, но он «наследил» ещё и в аэродинамике.

В рассуждениях Эйнштейна о подъёмной силе («Элементарная теория полёта и волн на воде» 1916. Берлин) есть только верхняя горбатая поверхность крыла и есть закон Бернулли: мол, крыло делит набегающий поток на два потока, из которых верхний, огибающий горб, всегда несколько быстрее прямого нижнего, а раз быстрее, то и меньше давление в нём; дескать, вот вам и положительная или подъёмная разница атмосферного давления на крыло. Но при этом его ни разу не посетила простая мысль вот о чём: при увеличении скорости крыла разница в скорости верхнего и нижнего потока остаётся той же самой, то есть 1/9 — 1/6; закон Бернулли действует и над, и под крылом. и как итог: при увеличении скорости самолёта подъёмная сила по закону Бернулли увеличиваться не может, то есть самолёт на горизонтальных крыльях просто-напросто не взлетит. Однако небольшая подъёмная сила горизонтального горбатого крыла всё же имеет место быть, но не по закону Бернулли, а по причине разрежения и завихрения воздуха за горбом, то есть по качественному закону потоков (отрицательно наклонная поверхность).

Как авторитетные авиаторы ни пытались хоть что-то объяснить знаменитому теоретику про угол атаки крыла и наклон всего самолёта к вектору движения, как о главной причине возникновения положительной разницы атмосферного давления, он лишь снисходительно посмеивался над ними (к примеру, переписка Эйнштейна с испытателем самолётов Паулем Георгом Эрхардтом). Дундуковость учёного всегда начинается с непонимания, незнания или с «незамечания» им сущей простоты и с желания выглядеть умным. Смотрите «Эйнштейн и подъёмная сила, или Зачем змею хвост». «Математика — единственный совершенный метод водить себя за нос» (Эйнштейн). и других — тоже. Вопросы профессору на засыпку: «Почему в рассуждениях теоретиков горбатого профиля закон Бернулли действует только над крылом?»; «Что доказал лейтенант Кульнев, совершивший в 1913 году затяжной горизонтальный полёт на перевернутом гидросамолете?» (Он доказал, что с хорошим движком и дверь полетит — был бы положительный угол атаки.)

Про математика Николая Жуковского и про его «присоединённые вихри», как о причине возникновения подъёмной силы, толкающей крыло снизу вверх, даже упоминать не хочется. Самолёты Эйнштейна и Жуковского — «беременная утка» и «шестикрылый монстр доаэродинамического периода» — не полетели по причине большого паразитного лобового сопротивления очень горбатых крыльев. Но именно они, а не Природа являются основоположниками и «отцами» аэродинамики. А ведь ещё Галилей завещал нам искать подсказки для ответов на все вопросы у Природы и в лабораториях, а не в научных текстах. Смотрите по запросу «Посмеёмся, мой Кеплер, великой глупости людской». «Великая глупость людская» — это глупость учёных. А их, учёных и учителей, и во времена Галилея было, мягко говоря, не мало.

Повторяем только что доказанный вывод: «Давление потока на параллельную ему поверхность всегда тем меньше давления в самом потоке, чем больше скорость этого потока и чем больше хаос в движении частиц пограничного слоя потока». «Степень хаоса» не вычисляется по математическим формулам, а «личная доля» каждого из двух законов потоков в наблюдаемых эффектах уменьшения давления потоков на поверхности с увеличением их скорости в каждом конкретном случае зависит от качества потоков и поверхностей, поэтому при желании тоже только измеряется, но не вычисляется. Вот почему математикам уже делать больше нечего — ни в аэродинамике, ни в объяснениях взаимодействий потоков с поверхностями. Так что, не только «Математика убивает креативность» (Андрей Фурсенко), но и креативность убивает математику. Причём математика убивает креативность всегда, а креативность убивает математику ещё недостаточно часто. «Занимаясь расчётами, ты попадаешь впросак, прежде чем успеваешь это осознать» (Эйнштейн). но чаще этого не замечаешь.

Однако вторым законом потоков объясняются не только опыты к теме «Закон Бернулли», но ещё один раз доказывается нечто совсем другое, позволяющее увидеть истоки математического идеализма в физике и похоронить математическую физику, как науку о природе. «Законы математики, имеющие какое-либо отношение к реальному миру, ненадёжны; а надёжные математические законы не имеют отношения к реальному миру» (А. Эйнштейн). Сейчас мы эту словесную формулу математического идеализма просто-напросто докажем. Вернее, я докажу, а вы. согласитесь.

Невесомые вещества – это хаосы: «Если нет веса у беспорядочно мечущейся частицы, то нет его и у целого» (Левкипп и Демокрит). Древние греки считали воздух невесомым веществом, но даже не все плазмы – это невесомые хаосы: «неорганизованная» плазма – это всем хаосам хаос; а «самоорганизованная» плазма — совсем не хаос. Последняя образуется в замкнутых объёмах или под внешним давлением и состоит из равноудалённых колеблющихся частиц. Напряжением взаимного отталкивания равноудалённых частиц «организованная» плазма способна разорвать любые оболочки или направленным действием пробить любую броню, что и используется инженерами-взрывниками уже довольно давно. (Смотрите по запросу «Самоорганизованная плазма».)

Самый яркий пример «неорганизованной» плазмы – это удалённая от поверхности плазменная атмосфера Солнца или его корона; самый простой пример «организованной» плазмы — пламя свечи, обжатое атмосферным давлением. Но у хаосов нет не только ни веса, ни существенного давления, но они ещё и непрозрачны ни для звука, ни для электромагнитных колебаний. К примеру, «неорганизованная» плазма, окружающая гиперзвуковую ракету, не позволяет управлять ракетой с помощью радиосигналов.

«Все жидкости и газы на Земле имеют вес и находятся под давлением веса собственных и выше расположенных слоёв» (Архимед). Поэтому все прозрачные жидкости и газы состоят из примерно одинаковых, равноудалённых и условно неподвижных (колеблющихся или дрожащих) частиц, находящихся в состоянии взаимного отталкивания и относительного (или чуткого) равновесия и взаимно отталкивающихся в газах на расстояниях много больших, чем в жидкостях. Отсюда: давление в любой точке водоёма или атмосферы равно напряжению взаимного отталкивания равноудалённых частиц в этой точке, и по силе оно равно весу всех частиц над этой точкой. Уберите атмосферное давление, и капля воды тут же исчезнет, разлетевшись на молекулы, а аквариум с водой словно взорвётся. И повинно в том будет как раз-таки «напряжение взаимного отталкивания равноудалённых частиц». Смотрите по запросу «Современный Архимед. Трактат «О плавающих телах» и «К физике антигравитонов». Там есть опыты, позволяющие буквально увидеть неподвижность колеблющихся частиц в жидкостях и в газах. Особенно показателен опыт по мгновенному замерзании переохлаждённой воды при её встряхивании в пластиковой бутылке. Многие его знают, но не понимают.

Способность атомов и молекул к движению взаимного отталкивания пропорциональна температуре. А температура – это «опосредованное мерило» интенсивности атомных и внутриатомных движений и величины гравитационных моментов (квантов, импульсов) атомов, передающихся от атома к атому путём индукции.

Гравитационные моменты у более возбуждённых атомов больше, а у «менее горячих» — меньше. Этими моментами атомы словно дёргают друг друга, понуждая сами себя к взаимному отталкиванию, к синхронности движений и к равновесию. Так осуществляется встречный индукционный или индуктивный теплообмен в природе и в гравитационной физике. О квантовой природе тяготения и отталкивания, электромагнетизма и прочего всего смотрите по запросу «Гравитационная физика. Атом».

Или вы думаете, что теоретики знают об атоме больше инженеров. Отнюдь. «Нет ни малейших признаков того, что атомная энергия когда-нибудь станет доступна людям. Это значило бы, что человек научился расщеплять атом» (Альберт Эйнштейн). «Десять лет моей жизни было потрачено только на то, чтобы полностью избавиться от идей этого человека» (Роберт Оппенгеймер об Эйнштейне и его теориях). Роберт Оппенгеймер — это инженер-изобретатель, «папа атомной бомбы». Он же на вопрос президента Гарри Трумэна «Когда русские смогут сделать атомную бомбу?» ответил: «Никогда». Дескать, в учебниках русских нет и намёка на реальную физику атома. И был абсолютно прав: русские сделали американскую атомную бомбу. Но в наших учебниках ничто не изменилось, словно атомного взрыва и не было. Смотрите по запросу «Гравитационная физика. Атом».

Теперь, думаю, вам уже более понятно — почему с увеличением скорости потока его давление на параллельную поверхность всегда уменьшается. Да, потому что при движении жидкого или газообразного кристалла вдоль шершавой поверхности возникает невесомый беспорядок в движении частиц пограничного слоя этого кристалла. Однако всё, что человек понимает, он когда-то понял сам — даже если ему в этом кто-то помог.

P.S. «Учёные объясняют то, что уже есть; инженеры создают то, чего никогда не было. И всё понятно, и всё работает. Мы же соединяем теорию с практикой: ничто не работает. и никто не знает почему» (Эйнштейн). У теоретиков ничто не работает потому, что у них «самая успешная математическая теория 20-го века» — это кинетическая теория теплоты и давления, не имеющая к физической реальности никакого отношения. Да и вся математическая или теоретическая физика — это то, чего не может быть. А то, что может быть, это — инженерная физика, то есть физика природных и искусственных технологий. И вообще, наука — это логичная совокупность всех явлений и всего известного опыта, а также поиск нового опыта. «Логичная» — значит, простая, явная, последовательная, взаимосвязанная и взаимообусловленная реальность, имеющая общую причинность.

Там, где нет науки, есть научность. Научность появляется именно там, где посредством математических действий и преобразований доказывается возможность невозможного, где одно непонятное объясняется посредством чего-то ещё более непонятного, где кому-то удаётся из очевидного сделать невероятное и где постулируется, то есть берётся за основу, то, что невозможно ни опровергнуть, ни доказать. Это словно злонамеренно рассчитано на то, что глупцам умным и научным кажется лишь то, чего они не понимают. «Конечно, ваша гипотеза безумна. Но достаточно ли она безумна. Если гипотеза недостаточно безумна, науке от неё не будет никакого толку» (Нильс Бор). а учёным — проку.

Простые и разумные идеи нужны только инженерам. И только они знают, что сложных открытий не бывает, что простота ближе к Природе и к пониманию Природы. но истинная простота — это как раз то, что впервые даётся познанию людей труднее всего. Но простота — это ещё и то, что учёным труднее всего объяснить. Более того, простота объяснения того или иного явления или опыта — это для теоретика хуже воровства и большое свинство. Дошло уже то того, что сказать правду учёным может только хам, антисемит и неуч. И только поэтому самым большим парадоксом является то, что этот мир всё же познаваемый (с).

И ещё. Всем теоретикам и преподавателям на засыпку: «Какой теорией руководствовались братья Райт, когда делали свой воздушный винт, который у них получился с КПД 78-80%, если научной аэродинамики ещё не было, а КПД самых современных пропеллеров из дерева не превышает 85%?».

Хотелось бы услышать возражения или замечания, но их почему-то нет. Видимо, с тем, что мы живём в эпоху математических лженаук, уже никто не спорит.

Воображеньем прозорливым
К догадкам верным нас несло…
Но сонм учёных кропотливых
Свернул наш поиск — на число.

И лязгом счёта оглушённый
Забыл наш ум — решенья ключ…
Стал слепнуть, в шоры цифр втеснённый.
А был так зряч и так могуч!

Уж цифре памятник построен,
Распята Истина на нём.
Поклонник счёта, жрец и воин
Простёрся ниц перед числом:

Не осознать бедняге в заблужденье,
Как много лжи за ширмой исчисленья!

🔍 Видео

Урок 146. Основное уравнение МКТ идеального газа - 2Скачать

Урок 133. Закон Бернулли. Уравнение БернуллиСкачать

Закон БернуллиСкачать

Урок 147. Задачи на основное уравнение МКТ идеального газаСкачать

Урок 132. Основные понятия гидродинамики. Уравнение непрерывностиСкачать

Уравнение состояния идеального газаСкачать

Уравнение Бернулли гидравликаСкачать

CFD. Течение в сопле. Уравнения Эйлера для сжимаемого газаСкачать

Уравнение Бернулли для газа. Олимпиадная физика. Be Student SchoolСкачать

Урок 151. Средняя кинетическая энергия молекул многоатомного газаСкачать