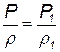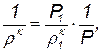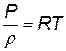Уравнение энергии для потока газа в механической форме (3 видео)

Содержание

ТЕРМОДИНАМИКА ГАЗОВОГО ПОТОКА
Уравнение энергии газового потока
Уравнение энергии в механической форме (уравнение Бернулли)
Уравнение Бернулли
Уравнение Бернулли
🎥 Видео

Видео:Уравнение Бернулли для потока жидкостиСкачать

ТЕРМОДИНАМИКА ГАЗОВОГО ПОТОКА

После изучения главы 5 бакалавр должен: знать

• вывод уравнения энергии газового потока;
• основные закономерности соплового и диффузорного адиабатного течения газа;
• дроссельный эффект Джоуля —Томсона; уметь
• выполнять расчеты располагаемой работы газового потока;
• выполнять расчеты истечения идеального газа из суживающихся и комбинированных сопел;
• выполнять расчеты истечения реальных газов и паров; владеть
• навыками использования уравнения энергии газового потока для расчетов истечения идеальных и реальных газов и паров.

Видео:Урок 133. Закон Бернулли. Уравнение БернуллиСкачать

Уравнение энергии газового потока

Процессы движения газа, происходящие в различных теплотехнических установках, связаны с преобразованием энергии в газовом потоке. Расчеты рабочих процессов этих установок строятся на общих положениях теории газового потока. Эта теория базируется на основных положениях термодинамики и на ряде допущений, два из которых представлены ниже.

1. Течение газа установившееся, т.е. в каждом выделенном сечении параметры газа во всех его точках остаются постоянными.
2. От сечения к сечению происходят бесконечно малые изменения параметров газа но сравнению со значениями самих параметров. Течение газа стационарное.

При таких допущениях газ при движении будет проходить ряд последовательных равновесных состояний.

Стационарное течение газа описывается системой уравнений, включающей уравнение неразрывности потока, уравнение состояния и уравнение энергии (уравнение первого закона термодинамики применительно к газовому потоку).

Уравнение неразрывности характеризует неизменность массового расхода газа в любом сечении канала при установившемся течении. Это уравнение имеет вид

где G — массовый секундный расход газа; F, F2 — площади поперечных сечений канала; W, w₂ — скорости в соответствующих сечениях; р_1? р₂ — плотности газа для тех же сечений потока (р = t/v).

Для одномерного газового потока в соответствии со вторым законом Ньютона (сила равна массе, умноженной на ускорение) можно записать соотношение [21]

где dp/dx — изменение давления по координате х, dw/dx — изменение скорости по координате х; ^dV= ^jdxF— сила, действующая на выделенный элементарный объем dV w(dw/dx) — ускорение элементарной массы газа dV.

Последнее соотношение можно переписать в виде

Учитывая, что р = 1/?;, получаем

Данное соотношение показывает, что приращения давления dp и скорости dw имеют разные знаки. Следовательно, скорость одномерного потока возрастает с уменьшением давления.

Величина -vdp совпадает с формулой для располагаемой работы dl₀ в уравнении первого закона термодинамики вида

Отсюда уравнение первого закона термодинамики для газового потока при отсутствии сил тяжести и сил трения в газе примет вид

где а—— приращение кинетической энергии газа на выделенном участке.

Так как i = и + pv> то

где d(pv) = pdv + vdp — элементарная работа проталкивания.

Последнее уравнение показывает, что теплота, сообщаемая газу, затрачивается па изменение внутренней энергии, на работу проталкивания и на изменение внешней кинетической энергии газа.

Видео:Закон БернуллиСкачать

Уравнение энергии в механической форме (уравнение Бернулли)

Уравнение энергии (3.18) содержит тепловые величины (q_нар, i₂, i₁) и не содержит давления и плотности газа. Можно получить иную механическую форму уравнения, куда, наоборот, не входит температура газа и тепло, а скорость движения связана с давлением и плотностью. Для этого воспользуемся формой записи первого закона термодинамики в виде

Уравнение энергии для потока газа в механической форме

(3.39)

После интегрирования с учетом того, что v=1/r имеем

(3.40)

Уравнение первого закона термодинамики записано для покоящейся жидкости или, что то же самое, для жидкости, движущейся вместе с системой координат. Учитывая это, вычтем из (3.18) уравнение (3.13), помня, что q=q_нар+q_T в результате получим

Это мы вправе делать, несмотря на то, что уравнение (3.23) записано для движущейся жидкости, так как значение температуры газа Т, количества тепла q, давления Р и плотности r не зависят оттого, в какой системе координат они измеряются.

Так как тепло трения равно работе, затрачиваемой на преодоление сил трения (q_ТР=l_ТР), то уравнению энергии можно придать следующий вид

(3.41)

Это уравнение, называемое уравнением Бернулли, имеет четкий физический смысл. Техническая работа, совершаемая газом (рис. 3.4, а)

расходуется на полезную работу расширения (например, в колесе турбины), на увеличение кинетической энергии газов

и на преодоление сил трения l_ТР

Посредством (3.41) можно вычислить, например, работу, которую отдает газ колесу турбины, стоящему между сечениями 1 и 2, если все остальные члены уравнения известны. Если величина / получится отрицательной, то это значит, что между сечениями 1 и 2 стоит компрессор и работа к газу подводится. Для того чтобы пользоваться уравнением Бернулли для сжимаемого газа, необходимо знать термодинамический процесс изменения состояния газа, так как без этого неизвестна зависимость плотности газа от давления, и нельзя вычислить интеграл (рис. 3.4, а).

Вычислим этот интеграл для основных термодинамических процессов. Для изохорического процесса p=const

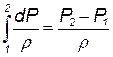(3.42)

Это соотношение используется в гидравлике, например, для определения мощности насоса или турбины.

При изобарическом процессе Р=const

(3.43)

Для изотермического процесса P/r=RT=const.

Из уравнения состояния

Это позволяет взять интеграл

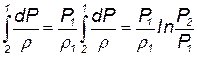(3.44)

Если состояние газа изменяется по идеальной адиабате

(3.45)

Для политропического процесса с постоянным показателем политропны P/r n =const

(3.46)

Важно отметить, что подводимое к газу тепло непосредственно не отражено в уравнении Бернулли. Однако оно учитывается при вычислении интеграла, т.к. влияет на вид функции р=f(Р), т.е. на характер процесса, по которому изменяется состояние газа.

Наибольшее значение в газовой динамике и теории реактивных двигателей имеет идеальный адиабатический процесс, который предполагает отсутствие теплообмена с окружающей средой и работы сил трения. Энтропия в таком процессе не изменяется. Если нет технической работы, и процесс идеальный адиабатический, то уравнение Бернулли (3.41) примет следующий вид

(3.47)

т.е. совершаемая газом техническая работа (рис. 3.4, а) целиком тратится на увеличение кинетической энергии газа.

Если поток газа при скорости, соответствующей числу М, затормозить полностью, то в соответствии с (3.31) его температура возрастет от значения T до T *

Если процесс торможения идет по идеальной адиабате, то, воспользовавшись уравнениями

0можно связать отношение температуры T * /T с отношением давлений

(3.48)

Подставив (3.48) в (3.31) получим

(3.49)

Аналогично свяжем отношение температуры T * /T с отношением r * /r

(3.50)

(3.51)

С помощью уравнения (3.37), связывающего отношение температур T * /T с приведенной скоростью, используя (3.39) и (3.40), можно получить

(3.52)

(3.53)

Истинное давление, которое получается при торможении струи газа, может существенно отличаться от полного давления, определенного из выражений (3.49) и (3.52).

Объясняется это тем, что в действительности торможение осуществляется не по идеальной адиабате, а с гидравлическими потерями, что, естественно, приводит к выделению тепла трения в потоке. Если на участке струи 1 — 2 наблюдаются потери, то это обязательно приводит к тому, что полное давление в сечении 2 будет ниже полного давления в сечении 1: Р₂ * * Величина гидравлических потерь оценивается коэффициентом сохранения полного давления

(3.54)

Чем больше потери, тем ниже значение коэффициента сохранения полного давления и меньше полное давление в сечении 2

(3.55)

Коэффициент сохранения полного давления связан с изменением энтропии в потоке газа, и, следовательно, с количеством выделившегося тепла в результате работы сил трения. Для того чтобы убедиться в этом, перейдем в равенстве (3.20) от параметров потока к параметрам торможения, используя соотношение Рv к =P * v *к =const. Получим

(3.56)

Выразив удельный объем через давление и температуру, используя уравнения состояния

и подставив v* в (3.56), после ряда преобразований можно получить

(3.57)

Так как полное давление в газовом потоке вследствие потерь падает Р * ₂ * ₁, тепло трения имеет всегда положительный знак (dq_тр>0) и соответственно энтропия возрастает (S₂>S₁,). Заменив в уравнении (3.57) отношение давлений через s, получим

Видео:Курс ""Турбомашины". Раздел 2.4 Уравнение энергии в мех. форме в отн.движении (лектор Батурин О.В.)Скачать

Уравнение Бернулли

Видео:Уравнение Бернулли гидравликаСкачать

Уравнение Бернулли

Тепловая форма уравнения энергии не обеспечивает связи между изменением скорости потока кинетической энергии и изменением давления. Такую связь можно получить, преобразовав уравнение энергии и придав ему механическую форму. Трение, которое не изменяет полную энергию потока, значительно влияет на изменение давления, основного механического параметра. Поэтому при выводе уравнения энергии в механической формуле необходимо учитывать трение. Мы предполагаем, что общее количество тепла, получаемого газом, состоит из 2 частей внешнего тепла которое подается в газ извне или выделяется в результате реакции горения и теплоты трения, которая выделяется в газе под действием силы трения. Энергия 3.

Является членом тепловой природы, достаточно заменить полученное выражение На a. Используйте первый закон термодинамики уравнение из ссылки 3. 5 3. 7 Подставляя эту формулу в уравнение энергии 3. 10, описанное с учетом работы теплоты и трения, получаем как видим, тепловые эффекты входят в обе стороны этого уравнения и взаимно разрушаются. Уравнения, в которых остается только механическая величина, удобнее писать в таком виде 8.

Для того чтобы лучистый теплообмен был пренебрежимо мал по сравнению с конвективным теплообменом, воздух, влажность которого требуется измерить, необходимо продувать через термометры с достаточной скоростью. Людмила Фирмаль

Это уравнение энергии, протекающей в механической форме. Конечная форма уравнения получается интегрированием уравнения 8. 7 и имеет вид 2 8. 8 П Уравнение слева от уравнения 8. 7 n 8. 8, как известно, называется одноразовой работой 3. 6. В результате уравнение энергии механического типа показывает, что имеющаяся работа газа расходуется при его движении на изменение кинетической энергии газа, на выполнение технической внешней работы, на выполнение фрикционной работы на преодоление силы трения.

Ранее указывалось, что можно рассчитать объем доступной работы только в том случае, если известно, как изменяется определенный объем газа в зависимости от изменения давления. То есть известно уравнение процесса v p 3 6. Формула 8. 8 является наиболее простой формой, когда плотность, а следовательно, и удельный объем не зависят от давления и температуры например, когда газ течет с малой скоростью или когда текут капли. Mr 1 p для sop81 Тогда уравнение энергии принимает вид П1-П2 Или Два 8. 9 Уравнение формы 8. 9 применяется к движению несжимаемых жидкостей в 1738 г. D. it был впервые получен путем bernoulli.

Вы можете видеть, что уравнение Бернулли является частным случаем более общего уравнения энергии. Уравнения механической энергии 8. 7 и 8. 8 называются обобщенными уравнениями Бернулли. Если учесть движение сжимаемых газов, то расчет доступной работы будет намного больше complicated. In в этом случае плотность не постоянна, она изменяется с изменением давления и температуры воздуха. Gas. At в то же время, как давление, так и температура изменяются одновременно, под влиянием различных причин скорости, технической работы, внешней теплопередачи, трения и др. В реальных компрессорах, турбинах и других газовых двигателях работа сил трения важна и не может быть проигнорирована.

Температура такого тела бывает ниже температуры воздуха, так как то тепло, которое передается телу от воздуха, поглощается в процессе испарения. Людмила Фирмаль

Работа трения влияет на уравнение не только в том, что сохраняется член g mp, но и в том, что теплота трения влияет на характер процесса изменения состояния gas. As как известно из предыдущего раздела 5. 10, сложный термодинамический процесс может быть описан с достаточной точностью политропным уравнением. ПГ Н const и В этом случае имеющаяся работа представляется формулой 5. 51. Таким образом, реальный процесс движения газа описывается уравнением Бернулли следующим образом Кей тр 8.