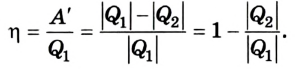
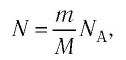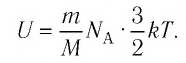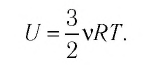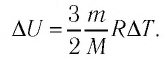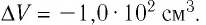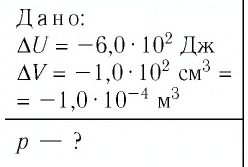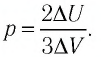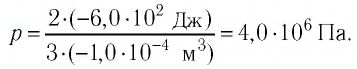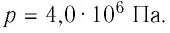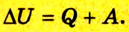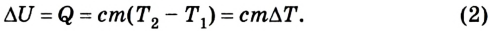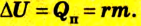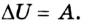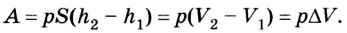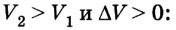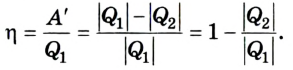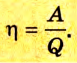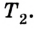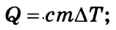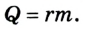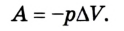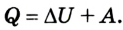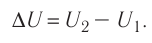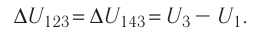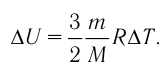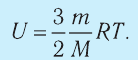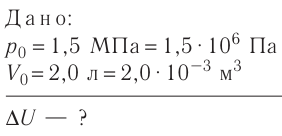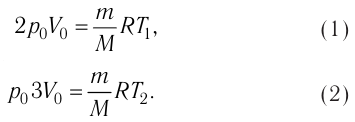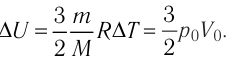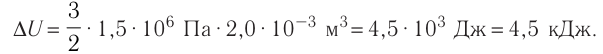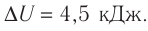ЛЕКЦИЯ № 2. Химическая термодинамика
Химическая термодинамика – наука, изучающая условия устойчивости систем и законы.
Термодинамика – наука о макросистемах.
Она позволяет apriori определить принципиальную невозможность того или иного процесса. Физические и химические явления в термодинамике исследуются с помощью основных законов термодинамики. Состояние рассматриваемых объектов в термодинамике определяется непосредственно измеряемыми величинами, характеризующими вещества; механизм процесса и сама структура вещества не рассматриваются.
В химической термодинамике изучается применение законов термодинамики к химическим и физико-химическим явлениям.
В ней рассматриваются главным образом:
1) тепловые балансы процессов, включая тепловые эффекты физических и химических процессов;
2) фазовые равновесия для индивидуальных веществ и смесей;
3) химическое равновесие.
Тепловые балансы составляют на основе первого закона термодинамики. На основе второго и третьего законов проводят анализ фазового и химического равновесий.
Изучение законов, которые описывают химические и физические равновесия, имеет огромное значение в химической термодинамике. Значение их позволяет решать задачи для производственной и научно-исследовательской работы. Рассмотрим основные задачи:
1) определение условий, при которых данный процесс становится возможным;
2) нахождение пределов устойчивости изучаемых веществ в тех или иных условиях;
3) устранение побочных реакций;
4) выбор оптимального режима процесса (давления, концентрации реагентов и т. д.).
Основные понятия и определения
1. Системы и их классификация
Система – тело или несколько тел, находящихся во взаимодействии между собой (диффузия, теплообмен, химическая реакция) и отделенных от окружающей среды.
Состояние системы в термодинамике определяется с помощью набора переменных, называемых параметрами состояния и характеризующих термодинамическое состояние при равновесии. Всякое изменение, происходящее в системе и связанное с изменением хотя бы одного из параметров состояния, называется термодинамическим процессом.
Системы имеют определенные границы, отделяющие их от внешней среды, и могут быть гомогенными или гетерогенными.
Гомогенная система – система, в которой все макроскопические свойства в любых ее частях имеют одно и то же значение или непрерывно меняются от точки к точке. Примеры: ненасыщенные растворы, пар, газовые смеси. Составленные части гомогенной системы не могут быть выделены из нее с помощью простых механических приемов (фильтрования, отбора и т. д.).
Гетерогенная система – система, составные части которой отделены друг от друга видимыми поверхностями раздела, на которых происходят резкие скачкообразные изменения какого-либо свойства. Примеры: насыщенный раствор какой-либо соли, находящийся в равновесии с кристаллами этой соли, две несмешивающиеся жидкости и т. д.). Составные части таких систем могут быть отделены друг от друга с помощью механических операций.
Совокупность тел, энергетически взаимодействующих между собой и с другими телами, обменивающихся с ними веществом, называется термодинамической системой.
Системы делят на изолированные (это те системы, которые не обмениваются энергией и веществом с другими системами), открытые (те системы, которые обмениваются с окружающей средой и веществом, и энергией), закрытые (системы, в которых есть только обмен энергией).
2. Термодинамические параметры. Термодинамические показатели. Баланс напряжений
Любая ТДС характеризуется параметрами: температура, давление, плотность, концентрация, мольный объем. В любой ТДС обязательно протекают процессы, и они могут быть равновесными, неравновесными, обратимыми и необратимыми.
Если в ТДС определенное свойство системы не будет изменяться во времени, т. е. оно будет одинаковым во всех точках объема, то такие процессы – равновесные.
В неравновесных процессах свойство системы будет изменяться во времени без воздействия окружающей среды.
Обратимые процессы – процессы, в которых система возвращается в первоначальное состояние.
Необратимые – когда система не возвращается в первоначальное состояние.
Функции могут зависеть от пути процесса. Функции, которые зависят от начального и конечного состояний системы и не зависят от пути процесса, – функции состояния; внутренняя энергия, энтальпия, энтропия и другие – полные дифференциалы.
Функции, которые зависят от начального и конечного состояний системы и зависят от пути процесса, не являются функциями состояния и не являются полными дифференциалами Q, A.
Функции можно разделить на две группы: экстенсивные и интенсивные.
Экстенсивное свойство системы прямо пропорционально массе системы и обладает аддитивностью (можно складывать): V, H, Uвн, S, G, F.
Интенсивное свойство системы не зависит от массы системы и не обладает свойством аддитивности: Q, A, T, P.
Давление – параметр состояния, определяемый силой, действующей в теле на единицу площади поверхности по нормали к ней. Оно характеризует взаимодействие системы с внешней средой.
Температура определяет меру интенсивности теплового движения молекул.
Значение градуса температуры и начало ее отсчета произвольны. В качестве эталона можно было бы выбрать не воду, а любое другое вещество (лишь бы его свойства однозначно изменялись с температурой, были воспроизводимы и легко поддавались измерению).
Такая произвольность исчезает, если пользоваться термодинамической (абсолютной) шкалой температур, основанной на втором законе термодинамики. Начальной точкой этой универсальной шкалы является значение предельно низкой температуры – абсолютный нуль, равный 273,15 о С.
Уравнение, связывающее термодинамические параметры системы в равновесном состоянии, – уравнение состояния.
Вследствие взаимосвязи между свойствами системы для определения ее состояния достаточно указать лишь некоторое число свойств. Так, состояние газа можно считать заданным, если указаны два параметра, например, температура и объем, а значение третьего параметра – давления – можно определить из уравнения состояния
Графически это уравнение является уравнением поверхности, построенной на трех взаимно перпендикулярных осях, каждая из которых соответствует одному термодинамическому параметру. Таким образом, термодинамическая поверхность – геометрическое место точек, изображающих равновесные состояния системы в функциях от термодинамических параметров.
Пусть дан изолированный сосуд, который разделен полупроницаемой перегородкой (рис. 1). В первой части сосуда температура Т1, во второй – температура Т2; Т1 > Т2.
Молекулы, ударяясь о полупроницаемую перегородку, будут отдавать часть энергии, а другие – принимать ее, без механического перемещения.
Форма передачи энергии от одной части системы к другой называется теплотой Q.
Мера переданной энергии от одной системы к другой – количество теплоты. Q не является функцией состояния и не является полным дифференциалом ?Q.
Работа процесса – это энергия, передаваемая одним телом другому при их взаимодействии, не зависящая от температуры этих тел и не связанная с переносом вещества от одного тела к другому.
Обмен энергией между системой и внешней средой обуславливается работой, совершаемой этой системой:
Работа (А) определяется суммой произведений сил, действующих на систему сил (давления и изменения объема).
Работа не является полным дифференциалом, ?А.
Если протекают равновесные процессы, то работа равновесного процесса будет максимальной величиной, по сравнению с неравновесным процессом
Если телу сообщают определенное количество теплоты, то это значит, что тело надо нагреть, а охладить систему – произвести действие, обратное нагреванию, т. е. отвести энергию.
Работа и теплота являются количественными характеристиками двух форм обмена энергией между системой и окружающей средой.
Понятие внутренней энергии
Внутренняя энергия системы Uвнскладывается из энергии поступательного и вращательного движения молекул, энергии внутримолекулярного колебательного движений атомов и атомных групп, энергии, заключающейся в ядрах атомов, энергии межмолекулярного взаимодействия.
Uвнявляется полным дифференциалом, она не зависит от пути процесса, а зависит от начального и конечного состояний системы, она однозначно непрерывна и конечна. Абсолютное значение Uвнопределить нельзя, можно определить только ее изменения.
Q и А качественно и количественно характеризуют форму передачи энергии, взаимосвязь между Q, A, Uвнустанавливает первый закон термодинамики.
К термодинамическим показателям относятся те, которые можно рассчитать, используя законы термодинамики, исходя из условий, что система находится в равновесии. Напряжение разложения:
где ?G – изменение термодинамического потенциала;
п – число электронов, участвующих в химической реакции;
F– число Фарадея.
где А – максимальная работа, которую способна совершить система в равновесном состоянии.
где Q – тепловой эффект реакций;
Up– термодинамическая характеристика электрохимической системы, которая мало зависит от условий электролиза.
Отклонение системы – поляризация. Электрохимическая реакция является гетерогенным процессом, и ее скорость может лимитироваться одной из стадий:
1) подвод реагирующего вещества к границе раздела фаз;
2) разряд и ионизация;
3) отвод продуктов реакции.
Поляризация, определяемая медленной стадией массопереноса – концентрационная. Если медленной стадией является стадия разряда ионизации, то поляризация называется перенапряжением. Природа и значение поляризации зависят от многих факторов: природа реагирующего вещества, материал электрода, состояние поверхности электрода, плотность тока, состав раствора и режим электролиза. Кинетический параметр – параметр, определяемый в реальных условиях электрохимической системы: ? тока, ЕАКТИВ, коэффициент диффузии, коэффициент переноса ? (на катод), ? (на анод) – доля расхода на процесс:
1) сила тока в электрохимическом аппарате J= iKSед загрузки, A, Z, iK – в зависимости от электролита;
2) скорость электролиза – образование массы вещества за единицу времени
где q – электрохимический эквивалент, v электролиза – J тока,
если в 1 см 2 – v – i тока.
Баланс напряжений. Напряжение на электрохимическом аппарате определяет расход электроэнергии при электролизе. Баланс напряжений на электрохимическом аппарате складывается из следующих составляющих:
где Еa– обратимый потенциал анода, В;
ЕК – обратимый потенциал катода, В;
?UЭЛ-ТА– падение напряжения в электролите, В;
?UДИФ– падения напряжения в диафрагме, В;
?UКОН– падение напряжения в контактах, В;
?UЭЛ – падение напряжения в электродах, В.
где i– плотность катодного тока;
?0 – удельное сопротивление электролита, ?0 повышается при вводе газа;
l – расстояние между электродами;
S – площадь сечения электролита;
Падение напряжения газозаполнения элемента определяется по формуле
Падение напряжения в диафрагме
Падение напряжения в контактах обычно принимают равным 5 – 10% от общего напряжения.
Падение напряжения в электродах:
Снижение напряжения на электрохимическом аппарате – оптимальное расстояние между электродами, максимальной электропроводностью.
К энергетическим характеристикам относятся:
1) напряжение на электрохимическом аппарате;
2) отдача по напряжению.
3) отдача по емкости
4) отдача по энергии
5) производительность электрохимического аппарата оценивается количеством продукта на одной затраченной энергии.
Расход электрической энергии на 1 тонну произведенного продукта определяется так:
ВT – выход по току в долях единицы.
Энергетический баланс – устанавливает соотношение между видом энергии, поступающей в электролизер, и энергией, уходящей из него, демонстрируя равенство статей прихода и расхода. Электроэнергия const тока, подводимая к электролизеру, составляет:
Общее уравнение энергетического баланса имеет следующий вид:
где ?Qприхода – тепловая энергия, поступающая в электролизер с электролитом и электродами за счет вторичных процессов;
Wэл.хим.р-ии – энергия тока, затраченная на электрохимическую реакцию;
Wтока – энергия тока, перешедшая в тепловую энергию; ?Qрасх– тепловая энергия, уносимая электролитом, электродами, газами при испарении Н2О, излучении и конвекции.
3. Первый закон термодинамики. Калорические коэффициенты. Связь между функциями CP и Cv
Формулировки первого закона термодинамики.
1. Общий запас энергии в изолированной системе остается постоянным.
2. Разные формы энергии переходят друг в друга в строго эквивалентных количествах.
3. Невозможно построить вечный двигатель первого рода, который бы давал механическую энергию, не затрачивая на это определенное количество молекулярной энергии.
4. Количество теплоты, подводимое к системе, расходуется на изменение Uвн и совершаемую работу.
5. Uвн– функция состояния, т. е. она не зависит от пути процесса, а зависит от начального и конечного состояния системы.
Пусть ТДС рассматривается при двух параметрах давления и объема, имеется два состояния системы I и II. Нужно перевести систему из состояния I в состояние II либо по пути А, либо по пути В (рис. 3).
Предположим, что по пути А изменение энергии будет ?UA, а по пути В – ?UB. Внутренняя энергия зависит от пути процесса
Согласно пункту 1 из формулировок первого закона термодинамики, общий запас энергии в изолированной системе остается постоянным
Uвн – функция состояния не зависит от пути процесса, а зависит от состояния системы I или II. Uвн – функция состояния, является полным дифференциалом
интегральная форма уравнения первого закона термодинамики.
для бесконечно малого процесса, ?A– сумма всех элементарных работ.
Теплота изотермического расширения:
Уравнение первого закона термодинамики в калорических коэффициентах
где l– коэффициент изотермического расширения;
Сv– теплоемкость при постоянном объеме.
теплоемкость при const давлении,
для реального газа.
Для идеального газа l= р
к = (?Q/дv)?– теплота изохорного расширения;
m = (?Q/дP)v– теплота изобарного сжатия.
4. Изопроцессы в термодинамике. Энергия Гельмгольца
1. Изотермический – Т= const
3. Изобарный – P = const
4. Адиабатический – ?Q = 0
действие, обратное логарифму – потенцирование
Уравнение первого закона термодинамики в калорических коэффициентах
где l– коэффициент изотермического расширения;
CV – теплоемкость при постоянном объеме.
теплоемкость при const давлении,
5. Процессы. Второй закон термодинамики
Второй закон термодинамики, в отличие от первого закона термодинамики, изучает все процессы, которые протекают в природе, и эти процессы можно классифицировать следующим образом.
Процессы бывают самопроизвольные, несамопроизвольные, равновесные, неравновесные.
Самопроизвольные процессы делятся на обратимые и необратимые. Второй закон термодинамики называют законом направленности процесса в изолированной системе (закон роста S). Слово «энтропия» создано в 1865 г. Р. Ю. Э. Клаузиусом – «тропе» с греческого означает превращение. В 1909 г. профессор П. Ауербах назвал царицей всех функций внутреннюю энергию, а S – тенью этой царицы. Энтропия – мера неупорядоченности системы.
Обратимые и необратимые процессы
Необратимые процессы идут без затраты работы, протекают самопроизвольно лишь в одном направлении, это такие изменения состояния в изолированной системе, когда при обращении процессов свойства всей системы меняются. К ним относятся:
1) теплопроводность при конечной разности температур;
2) расширение газа при конечной разности давлений;
3) диффузия при конечной разности концентраций.
Обратимыми процессами в изолированной системе называются такие процессы, которые можно обратить без каких-либо изменений в свойствах этой системы.
Обратимые: механические процессы в системе, где отсутствует трение (идеальная жидкость, ее движение, незатухающие колебания маятника в вакууме, незатухающие электромагнитные колебания и распространение электромагнитных волн там, где нет поглощения), которые могут возвратиться в начальное состояние.
Самопроизвольные – процессы, которые идут сами собой, на них не затрачивается работа, они сами могут производить ее (движение камней в горах, Na с большой скоростью движется по поверхности, так как идет выделение водорода проверить.).
Несамопроизвольные – процессы, которые не могут идти сами собой, на них затрачивается работа.
Равновесие делится на устойчивое, неустойчивое и безразличное.
Постулаты второго закона термодинамики.
1. Постулат Клаузиуса – не может быть перехода тепла от менее нагретого к более нагретому телу.
2. Постулат Томсона – теплота наиболее холодного тела не может служить источником работы.
Теорема Карно – Клаузиуса: все обратимые машины, совершающие цикл Карно с участием одного и того же нагревателя и одного и того же холодильника, имеют одинаковый коэффициент полезного действия, независимо от рода рабочего тела.
Аналитические выражения второго закона термодинамики.
1. Классическое уравнение второго закона термодинамики
Q1 /Т1– приведенное тепло нагревателя;
Q2 / T2 – приведенное тепло холодильника;
Q1 /Т1= Q2 /Т2 – равенство приведенных теплот нагревателя и холодильника. Это второе уравнение термодинамики.
Если делим адиабатами на множество циклов Карно, то получим
Это третье уравнение второго закона термодинамики для бесконечно малого цикла Карно.
Если процесс является конечным, то
Это четвертое уравнение второго закона термодинамики Если процесс является замкнутым, то
Это пятое уравнение второго закона термодинамики для обратимого процесса.
Интеграл по замкнутому контуру – интеграл Клаузиуса.
При необратимом процессе:
Это шестое уравнение второго закона термодинамики, или уравнение Клаузиуса, для обратимого процесса равно нулю, для необратимого процесса оно меньше 0, но иногда может быть больше 0.
это седьмое уравнение второго закона термодинамики. Второй закон термодинамики – закон роста S.
Действие, обратное логарифму – потенцирование:
Первый закон термодинамики определяется постоянством функции U в изолированной системе. Найдем функцию, выражающую содержание второго закона, а именно, одностороннюю направленность протекающих в изолированной системе процессов. Изменение искомой функции должно иметь для всех реальных, т. е. необратимых процессов, протекающих в изолированных системах, один и тот же знак. Второй закон термодинамики в приложении к некруговым необратимым процессам должен выражатся неравенством. Вспомним Цикл Карно. Так как любой цикл можно заменить бесконечно большим числом бесконечно малых циклов Карно, то выражение:
справедливо для любого обратимого цикла. Считая на каждом элементарном участке теплообмена Т = const, найдем, что:
и для всего цикла
Энергия Гельмгольца Изохорно-изотермический потенциал
Величина (V – TS) является свойством системы; она называется энергией Гельмгольца. Была введена Гельмгольцем в 1882 г.
dF = dU – TdS – SdT,
dF = TdS – pdV – SdT,
F – полный дифференциал.
Увеличение объема приводит к тому, что изохорно-изотермический потенциал уменьшается (тот «минус», который стоит перед Р ). Повышение температуры приводит к тому, что F уменьшается.
физический смысл изохорно-изотермического потенциала.
Убыль изохорно-изотермического потенциала равна максимальной работе, производимой системой в этом процессе; F – критерий направленности самопроизвольного процесса в изолированной системе. Для самопроизвольного процесса: AFT г 0. Для равновесного процесса: ?FT,V = 0.
Изохорно-изотермический потенциал в самопроизвольных процессах уменьшается и, когда он достигает своего минимального значения, то наступает состояние равновесия (рис. 4).
где 1 – самопроизвольный процесс;
2 – несамопроизвольный процесс;
3 – равновесный процесс.
1) G (P, Т= cоnst), энергия Гиббса
G = U – TS + PV = H – TS = F + PV,
Работа изобарно-изотермического процесса равна убыли изобарно-изотермического потенциала – физический смысл этой функции;
2) функция – полный дифференциал, однозначна, конечна, непрерывна.
dG = dU – TdS – SdT + pdv + vdp,
dG = TdS – pdV – TdS – SdT + pdv + vdp,
Повышение температуры приводит к тому, что изобарно-изотермический потенциал уменьшается, так как перед S стоит знак «минус». Повышение давления приводит к тому, что изобарно-изотермический потенциал увеличивается, так как перед V стоит знак «плюс»;
3) G как критерий направленности процесса в изолированной системе.
Для самопроизвольного процесса: (?G)P,T 0. Для равновесного процесса: (?G)P,T = 0
Изобарно-изотермический потенциал в самопроизвольных процессах уменьшается, и, когда он достигает своего минимума, то наступает состояние равновесия.
где 1 – самопроизвольный процесс;
2 – равновесный процесс;
3 – несамопроизвольный процесс.
Совершается работа за счет ?U и ?H.
Противодействующие факторы. Энтальпийный фактор характеризует силу притяжения молекул. Энтропийный фактор характеризует стремление к разъединению молекул.
Энтальпия – Н Внутренняя энергия – U.
dH = dU + pdv + vdp,
dU = TdS – SdT + pdV + Vdp,
dH = –pdV + pdV + Vdp; U = TdS + VdP.
где 1 – самопроизвольный процесс,
2 – несамопроизвольный процесс,
3 – равновесный процесс,
Уравнения Гиббса – Гельмгольца – уравнения максимальной работы.
Они позволяют установить связь между максимальной работой равновесного процесса и теплотой неравновесного процесса
уравнение Гельмгольца (уравнение связывающее функции F и G с их температурными производными).
уравнение Гиббса (уравнение связывающее функции F и G с их температурными производными).
Уравнения эти дают возможность рассчитать работу через температурный коэффициент функции Гельмгольца или через температурный коэффициент функции Гиббса.
Оно позволяет применить второй закон термодинамики к фазовым переходам. Если рассчитать процессы, в которых совершается только работа расширения, то тогда изменение внутренней энергии
Предположим, что 1 моль вещества переходит из первой фазы во вторую.
нет условного равновесия,
где dP/dT – температурный коэффициент давления,
где ?фп – теплота фазового перехода.
уравнение Клаузиуса-Клапейрона, дифференциальная форма уравнения.
Уравнение устанавливает взаимосвязь между теплотой фазового перехода, давлением, температурой и изменением молярного объема.
эмпирическая форма уравнения Клаузиуса-Клапейрона.
Уравнение Клаузиуса-Клапейрона изучает фазовые переходы. Фазовые переходы могут быть I рода и II рода.
I рода – характеризуются равенством изобарных потенциалов и скачкообразными изменениями S и V.
II рода – характеризуются равенством изобарных потенциалов, равенством энтропий и равенством молярных объемов.
Алгебраическая сумма приведенных теплот для любого обратимого кругового процесса равна нулю.
Эта подынтегральная величина – дифференциал однозначной функции состояния. Эта новая функция была введена Клаузиусом в 1865 г. и названа энтропией – S (от греч. «превращение»).
Любая система в различном состоянии имеет вполне определенное и единственное значение энтропии, точно так же, как определенное и единственное значение Р, V, Tи других свойств.
Итак, энтропия выражается уравнением:
где S – это функция состояний, изменение которой dSв обратимом изотермическом процессе перехода теплоты в количество Q равно приведенной теплоте процесса.
При независимых переменных U (внутренняя энергия) может обозначаться UВН и V (объем), или Р (давление) и Н(энтальпия). Энтропия является характеристической функцией. Характеристические функции – функции состояния системы, каждая из которых при использовании ее производных дает возможность выразить в явной форме другие термодинамические свойства системы. Напомним, в химической термодинамике их пять:
1) изобарно-изотермический потенциал (энергия Гиббса) при независимых переменных Т, Р и числе молей каждого из компонентов и.;
2) изохорно-изотермический потенциал (энергия Гельмгольца) при независимых переменных Т, V, ni;
3) внутренняя энергия при независимых переменных: S, V, ni;
4) энтальпия при независимых переменных: S, Р, пi;
5) энтропия при независимых переменных Н, Р, ni..
В изолированных системах (U и V= const) при необратимых процессах энтропия системы возрастает, dS > 0; при обратимых – не изменяется, dS = 0.
Связь энтропии с другими термодинамическими параметрами
Для того, чтобы решить конкретную задачу, связанную с применением энтропии, надо установить зависимость между ней и другими термодинамическими параметрами. Уравнение dS = ?Q/T в сочетании с ?Q = dU + PdV и ?Q = dH – VdP дает уравнения:
применительно к функциональной зависимости ?(Т, V, S) = 0, получим
Теперь найдем зависимость энтропии от температуры из уравнений:
Вот эти зависимости:
Эти два уравнения являются практически наиболее важными частными случаями общего соотношения:
Пользуясь разными зависимостями, можно вывести другие уравнения, связывающие термодинамические параметры.
Самопроизвольные – процессы, которые идут сами собой, на них не затрачивается работа, они сами могут производить ее (движение камней в горах, натрий с большой скоростью движется по поверхности, так как идет выделение водорода), а калий буквально «прыгает» по воде.
Несамопроизвольные – процессы, которые не могут идти сами собой, на них затрачивается работа.
Равновесие делится на устойчивое, неустойчивое и безразличное.
Постулаты второго закона термодинамики.
1. Постулат Клаузиуса – «Не может быть перехода тепла от менее нагретого к более нагретому телу».
2. Постулат Томсона – «Теплота наиболее холодного тела не может служить источником работы».
Теорема Карно-Клаузиуса: «Все обратимые машины, совершающие цикл Карно с участием одного и того же нагревателя и одного и того же холодильника, имеют одинаковый коэффициент полезного действия, независимо от рода рабочего тела».
Аналитические выражения второго закона термодинамики.
1. Классическое уравнение второго закона термодинамики
где Q /Т – приведенное тепло;
Q1 /Т1– приведенное тепло нагревателя;
Q2 / T2 – приведенное тепло холодильника;
Q1 /Т1= Q2 / T2 – равенство приведенных теплот нагревателя и холодильника. Это второе уравнение термодинамики.
Если делим адиабатами на множество циклов Карно, то получим
Это третье уравнение второго закона термодинамики для бесконечно малого цикла Карно.
Если процесс является конечным, то
Это четвертое уравнение второго закона термодинамики
Если процесс является замкнутым, то
Это пятое уравнение второго закона термодинамики для обратимого процесса.
Интеграл по замкнутому контуру – интеграл Клаузиуса.
При необратимом процессе:
шестое уравнение второго закона термодинамики, или уравнение Клаузиуса, для обратимого процесса равно нулю, для необратимого процесса оно меньше 0, но иногда может быть больше 0.
это седьмое уравнение второго закона термодинамики. Второй закон термодинамики – закон роста S.
это формула Больцмана,
где S – энтропия – степень разупорядоченности системы;
k– постоянная Больцмана;
W – термодинамическая вероятность системы макросостояний.
Термодинамическая вероятность – число микросостояний данной системы, с помощью которых можно реализовать данное макросостояние системы (Р, Т, V).
Если W = 1, то S = 0, при температуре абсолютного нуля –273°С все виды движений прекращаются.
Термодинамическая вероятность – это число способов, которыми атомы и молекулы можно распределить в объеме.
Цикл Карно – круговой тепловой процесс, в результате которого некоторое количество тепла термодинамически обратимым способом переносится от горячего тела к холодному. Процесс должен совершаться таким образом, чтобы тела, между которыми происходит непосредственный обмен энергией, находились при постоянной температуре, т. е. и горячее и холодное тела считаются настолько большими тепловыми резервуарами, что температура первого при отнятии и температура второго при прибавлении рассматриваемого количества тепла ощутимо не изменяются. Для этого необходимо «рабочее тело». Рабочим телом в этом цикле является 1 моль идеального газа. Все процессы, составляющие цикл Карно, являются обратимыми. Рассмотрим их. На рисунке 9 показано:
АВ – изотермическое расширение газа от V1 до V2 при температуре T1, количество теплоты Q1 поглощается;
CD – сжатие изотермическое от V3до V4 осуществляется при температуре Т2, количество теплоты Q отдается;
Проанализируем его подробно. Для процесса необходимо «рабочее тело», которое сначала при более высокой температуре Т1 приводится в соприкосновение с горячим телом и изотермически получает от него указанное количество тепла. Затем оно адиабатически охлаждается до температуры Т2, отдавая при этой температуре тепло холодному телу с температурой Т2, а затем адиабатически возвращается в начальное состояние. В цикле Карно ?U = 0. При проведении цикла «рабочее тело» получило количество теплоты Q1 – Q2 и произвело работу А, равную площади цикла. Итак, в соответствии с первым законом термодинамики Q1 – Q2 = А, получаем:
Для адиабатических процессов можно записать:
Поделим первое уравнение на второе. В результате имеем:
Получаем уравнение для работы:
Теперь получим КПД:
Итак, КПД цикла Карно зависит от температуры теплоотдатчика и теплоприемника. Эта величина имеет тем большее значение, чем выше T1 и ниже T2. Цикл Карно необходим при разрешении вопроса о КПД тепловых машин.
7. Невозможность вечного двигателя
Даже в самой современной высокопроизводительной машине часть теплоты не может быть превращена в работу. Чтобы это осуществить, нужна машина, работающая в пределах температуры теплоприемника и более низкой температуры теплоотдатчика.
Значит, невозможно построить двигатель, в котором рабочее тело совершало бы работу, вступая в теплообмен с одним только, и при-чем единственным, источником теплоты, то есть нельзя осущест-вить вечный двигатель второго рода. Из этой формулировки логически вытекает следующая: нельзя превратить теплоту какого-либо тела в работу, не производя никакого другого изменения, кроме охлаждения этого тела. Это доказывает одно: что невозможно при помощи кругового изотермического процесса произвести работу. Попробуем сформулировать неосуществимость вечного двигателя первого рода. Ее можно рассматривать двояко: с одной стороны, «работу нельзя создать из ничего», с другой стороны, «работу нельзя превратить в ничто». Хаотическое тепловое движение частиц более вероятно, чем их направленное движение. «Появление» теплоты всегда знаменуется превращением энергии в малоэффективную форму. Вероятность того, что молекулы, движущиеся хаотично, получат определенную ориентацию, ничтожна. Если бы это существовало на самом деле, то привело бы к появлению направленной силы, способной совершать работу. Поэтому переход без ограничений теплоты в работу невозможен, хотя работа может перейти в теплоту целиком. Итак, при отсутствии теплоприемника запас энергии теплоотдатчика не может быть использован. Нельзя использовать безграничные запасы энергии воздуха, морей, океанов и т. д.
- Термодинамика — основные понятия, формулы и определения с примерами
- Термодинамическая система
- Внутренняя энергия
- Внутренняя энергия одноатомного идеального газа
- Способы изменения внутренней энергии
- Работа в термодинамике
- Работа газа
- Что такое термодинамическая система
- Что такое внутренняя энергия
- Внутренняя энергия идеального одноатомного газа
- Пример решения задачи №1
- Внутренняя энергия тела
- Работа газа
- Первый закон термодинамики
- Тепловые двигатели
- Основные определения и формулы
- Основы термодинамики
- Пример решения задачи №2
- Уравнение энергетического баланса термодинамической системы
- 🎥 Видео
Видео:Урок 175. Уравнение теплового балансаСкачать

Термодинамика — основные понятия, формулы и определения с примерами
Содержание:
Термодинамические системы и макропараметры состояния вещества:
Термодинамический подход основывается на понятии термодинамической системы, которая представляет собой любое макроскопическое тело или совокупность таких тел. Состояние термодинамической системы определяется ее внутренними параметрами, например состоянием движения микрочастиц, из которых состоит тело. Тепловое состояние тела, которое характеризуется температурой, тесно связано со скоростью движения атомов и молекул — чем больше скорость их движения, тем выше температура тела.
Температура тела зависит от скорости движения атомов и молекул, из которых оно состоит, — чем больше скорость, тем выше температура.
Внутреннее состояние тела очень сложно определить через параметры движения микрочастиц, потому что их очень много. Поэтому, чтоб упростить описание состояния термодинамической системы, его связывают с физическими величинами, которые характеризуют тело в целом, независимо от его молекулярного строения. К таким величинам принадлежат, в частности, масса, объем, плотность, давление, температура и т. п.
Их называют макропараметрами системы. Фактически они являются усредненными значениями данных физических величин на протяжении длительного времени.
Температура — один из основных макропараметров термодинамической системы, характеризующий состояние ее теплового или термодинамического равновесия. Сущность данного понятия объясняется течением тепловых явлений и процессов.
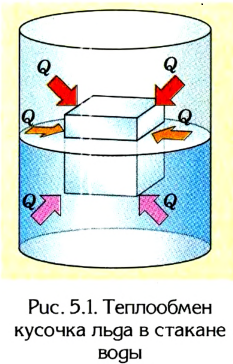
Например, из собственного опыта нам известно, что более нагретые тела отдают теплоту менее нагретым, вследствие чего со временем их температуры станут одинаковыми. Если, к примеру, кусочек льда бросить в стакан с теплой водой (рис. 5.1), то лед будет таять, а вода в стакане охлаждаться, отдавая определенное количество теплоты тающему льду. Кроме того, стакан с водой и лед пребывают в состоянии теплообмена с окружающей средой. Поэтому со временем температуры всех этих тел станут одинаковыми.
Тела с более высокой температурой отдают тепловую энергию телам с более низкой температурой; теплообмен происходит до тех пор, пока их температуры не станут одинаковыми.
Следовательно, со временем вследствие теплообмена в термодинамических системах наступает состояние термодинамического равновесия, когда температуры всех тел становятся одинаковыми и теплообмен между ними прекращается. Значение температуры характеризует вполне определенное состояние теплового равновесия термодинамической системы, в котором она пребывает в данный момент. Он может быть изменен в результате термодинамического процесса.
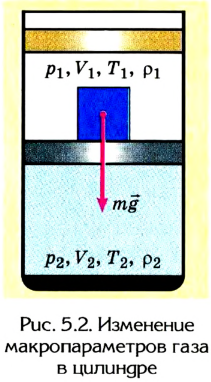
Если, например, на поршень в цилиндре с газом положить груз (рис. 5.2), то объем газа будет изменяться до тех пор, пока давление не сравняется с внешним давлением. Т. е. термодинамическая система «цилиндр — газ» перейдет в иное состояние, характеризующееся новыми значениями макропараметров — давлением 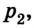
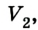
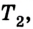
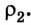
Термодинамика рассматривает в основном состояния термодинамического равновесия и процессы, которые происходят достаточно медленно, и поэтому каждое новое их состояние можно считать равновесным. В состоянии термодинамического равновесия между макропараметрами системы существуют определенные функциональные зависимости, отображаемые уравнениями состояния термодинамической системы.
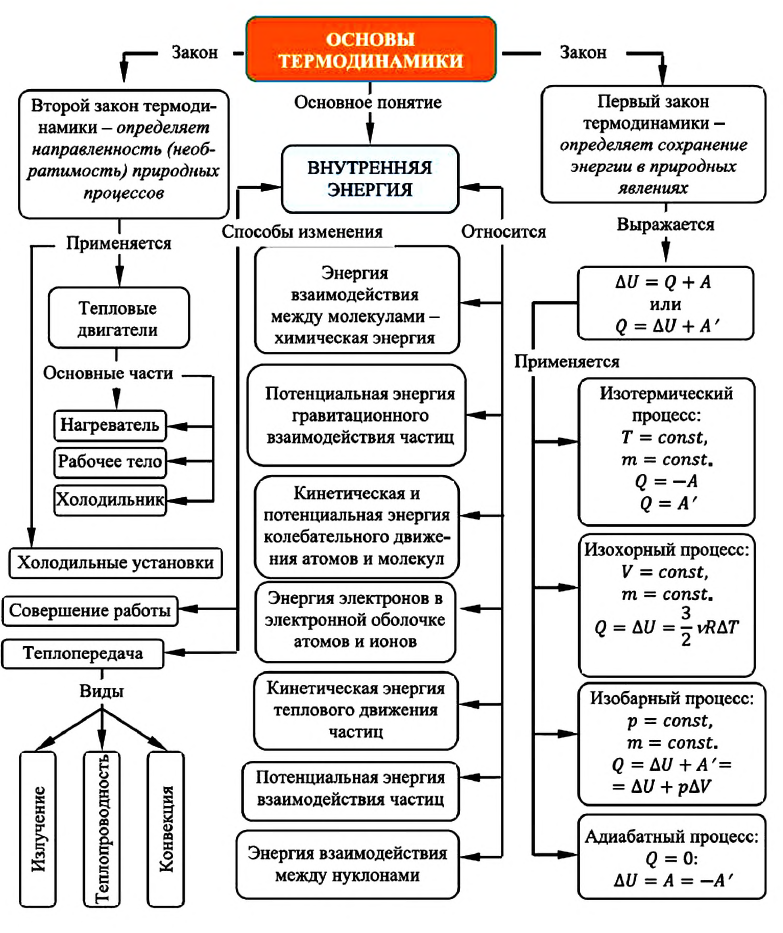
Карта основ термодинамики:
Видео:ОВР и Метод Электронного Баланса — Быстрая Подготовка к ЕГЭ по ХимииСкачать

Термодинамическая система
Раздел физики, изучающий тепловые явления в макроскопических системах, называется термодинамикой. В основе термодинамики лежат термодинамические законы, опирающиеся на большое количество экспериментальных фактов. Эти законы отвечают на вопрос «как?», например, как изменяется состояние тела (твердого тела, жидкости или газа) при нагревании (или охлаждении), в каком направлении и как передается тепло, как изменяется температура газа при его расширении и другие. Объектами исследования термодинамики являются термодинамические системы.
Любое макроскопическое тело или система макроскопических тел называется термодинамической системой. Состояние термодинамической системы характеризуется макроскопическими или термодинамическими параметрами (масса, плотность, объем, давление, температура).
Внутренняя энергия
Величины, определяющие состояние термодинамической системы в данный момент времени, то есть соответствующие этому состоянию макроскопические параметры, называются функциями состояния. Основной среди этих величин является внутренняя энергия.
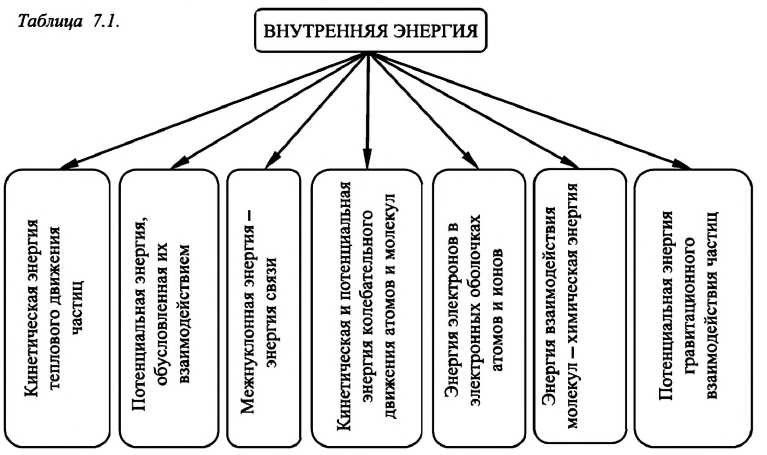
Внутренняя энергия — это сумма кинетических энергий различных видов, движения частиц системы и потенциальных энергий взаимодействия этих частиц (см.: таблица 7.1).
Внутренняя энергия термодинамической системы является функцией температуры и объема, определяющих состояние системы:
Внутренняя энергия одноатомного идеального газа
Газ, молекулы которого состоят из одного атома, называют одноатомным газом. Внутренняя энергия одноатомного газа равна сумме кинетических энергий поступательного движения частиц и потенциальных энергий их взаимодействия:
Однако внутренняя энергия идеального газа данной массы равна сумме средних кинетических энергий хаотического движения частиц:
Средняя кинетическая энергия одной частицы одноатомного идеального газа определяется выражением 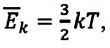
Это выражение является формулой закона Джоуля:
Внутренняя энергия идеального газа зависит от ее массы, рода (молярной массы) и температуры. Даже если давление и объем газа изменятся, при постоянной температуре его внутренняя энергия не изменится.
Сопоставив формулу (7.1) с выражением Менделеева-Клапейрона, получим:
Способы изменения внутренней энергии
Для изменения внутренней энергии термодинамической системы необходимо изменить или среднюю кинетическую энергию теплового движения молекул системы, или потенциальную энергию их взаимодействия, или же изменить обе энергии одновременно. Из многочисленных опытов было определено, что существует два способа изменения внутренней энергии: теплопередача и совершение работы.
Изменение внутренней энергии системы происходит двумя способами: передачей количества теплоты 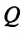
Если внутренняя энергия изменяется только в результате теплообмена, то изменение внутренней энергии равно полученному (или отданному) системой количеству теплоты. Например, при нагревании и охлаждении тела изменение его внутренней энергии определяется так:
Изменение внутренней энергии в процессе плавления твердого тела или кристаллизации жидкости происходит за счет изменения потенциальной энергии взаимодействия молекул тела. Изменение внутренней энергии при этих процессах численно равно теплоте плавления (кристаллизации):
Где 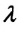
Изменение внутренней энергии тела в процессе парообразования и конденсации также равно затраченному во время этого процесса количеству теплоты:
Где 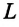
Изменение внутренней энергии одноатомного идеального газа определяется изменением его температуры:
Где 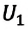
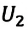
Внимание. Изменение внутренней энергии термодинамической системы зависит не от вида процесса, а от его начального и конечного состояния.
Работа в термодинамике
Если изменение внутренней энергии происходит только в результате совершения механической работы, то это изменение равно или работе внешних сил над системой 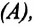
Работа в термодинамике — это одна из мер изменения внутренней энергии термодинамической системы.
Работа газа
Предположим, что в толстостенном цилиндре находится газ, сжимаемый поршнем. При сжатии поршень передает часть своей кинетической энергии молекулам газа, в результате чего увеличивается внутренняя энергия газа и повышается его температура — внешние силы совершают работу над газом. При расширении, наоборот, молекулы газа, передавая часть своей кинетической энергии поршню, уменьшают свою скорость и газ охлаждается — он совершает работу над внешними силами (b).
Таким образом, работа, совершенная газом над внешними силами, в результате расширении газа данной массы при постоянном давлении равна:
Работа же, совершенная внешними силами над газом равна :
Где 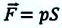
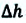
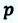
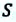

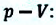
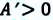
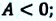
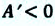
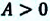
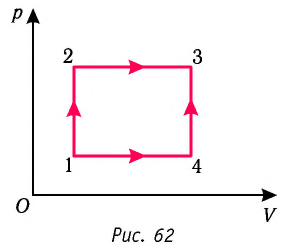
Если в процессе совершения работы газ через некоторое время возвращается в первоначальное состояние, то такой процесс называется замкнутым или циклическим процессом.
Если стрелки, показывающие направление циклического процесса, совпадают с направлением вращения часовых стрелок, то работа газа положительна, а работа внешних сил отрицательна (d). Если же стрелки, определяющие направление процесса, направлены против вращения часовых стрелок, то работа газа отрицательна, а работа внешних сил положительна.
Что такое термодинамическая система
Полную энергию физической системы можно представить как алгебраическую сумму её механической энергии и внутренних энергий тел, образующих систему. Убыль механической энергии системы в ряде случаев происходит при самопроизвольном переходе её части во внутреннюю энергию тел системы. Так, например, режущие инструменты заметно нагреваются при заточке. При скольжении конькобежца под коньками тает лёд, что обеспечивает хорошее скольжение. В этих примерах тела при трении нагреваются, и интенсивность теплового движения их молекул возрастает, что приводит к увеличению внутренней энергии тел. Как же определить внутреннюю энергию термодинамической системы? И что понимают под термодинамической системой?
В термодинамике физические тела и их модели называют термодинамическими системами. Для их описания используют параметры системы, такие, как давление, объём, температура (макропараметры), а не физические характеристики молекул (микропараметры). Макропараметры можно непосредственно измерить, используя приборы, или выразить через другие величины, которые можно измерить на опыте. Мы рассмотрим простейшие термодинамические системы, состояние которых определяют, используя только давление, объём и температуру.
Тела, образующие термодинамическую систему, могут обмениваться с окружающей средой энергией, а также веществом. Если этого не происходит, то термодинамическую систему называют замкнутой или изолированной.
Что такое внутренняя энергия
Рассматривая полную энергию макроскопического тела, необходимо учитывать не только его механическую энергию (кинетическую и потенциальную), но также и энергию, заключённую внутри самого тела, — внутреннюю энергию.
Внутренняя энергия макроскопического тела — алгебраическая сумма кинетической энергии теплового движения всех частиц, образующих тело, и потенциальной энергии их взаимодействия.
Внутренняя энергия любой термодинамической системы состоит из внутренних энергий тел, входящих в данную систему, и является одной из основных физических величин, используемых в термодинамике.
В термодинамике представляет интерес не само значение внутренней энергии системы, а её изменение. Поэтому обычно принимают во внимание только те составляющие внутренней энергии, которые изменяются в рассматриваемых процессах.
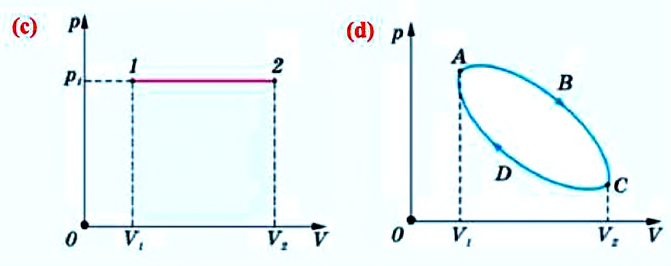
Рассмотрим переход некоторой массы идеального газа из состояния 1, в котором его внутренняя энергия 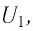
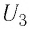
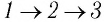
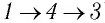
Внутренняя энергия зависит от конкретного состояния системы. Это означает, что изменение внутренней энергии при переходе термодинамической системы из одного состояния в другое зависит только от значений параметров этих состояний и не зависит от процесса перехода.
- *
— приращение физической величины, т. е. разность между её конечным и начальным значениями;
— убыль величины, т. е. разность между её начальным и конечным значениями.
Внутренняя энергия идеального одноатомного газа
Определим внутреннюю энергию идеального одноатомного газа, т. е. газа, образованного атомами. Например, одноатомными газами являются инертные газы — гелий, неон, аргон и др.
Из определения понятия «идеальный газ» следует, что его внутренняя энергия является суммой кинетических энергий хаотического движения всех атомов (или молекул) (потенциальная энергия взаимодействия между частицами отсутствует). Следовательно, внутренняя энергия идеального одноатомного газа равна произведению средней кинетической энергии 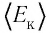
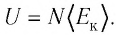
где 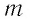
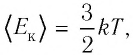
С учётом того, что произведение постоянной Больцмана и постоянной Авогадро 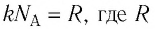
Из формулы (11.1) следует, что внутренняя энергия данной массы идеального одноатомного газа пропорциональна его абсолютной температуре. Она не зависит от других макроскопических параметров состояния — давления и объёма. Следовательно, изменение внутренней энергии данной массы одноатомного идеального газа происходит только при изменении его температуры:
При определении внутренней энергии реальных газов, жидкостей и твёрдых тел необходимо учитывать потенциальную энергию взаимодействия частиц, которая зависит от расстояния между ними. Поэтому в общем случае внутренняя энергия макроскопических тел зависит не только от абсолютной температуры, но и от объёма.
Изменить внутреннюю энергию термодинамической системы можно двумя способами: используя теплообмен и совершая работу. Процесс теплообмена и совершение работы характеризуют соответственно физическими величинами — количеством теплоты Q и работой А, которые являются мерами изменения внутренней энергии системы.
Пример решения задачи №1
При изобарном охлаждении внутренняя энергия идеального одноатомного газа изменилась на 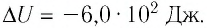
Решение. Приращение внутренней энергии некоторого количества идеального одноатомного газа
Используя уравнение Клапейрона—Менделеева, можно осуществить замену:

Решая совместно уравнения (1) и (2), получим:
Ответ:
Внутренняя энергия тела
Любое макроскопическое тело обладает энергией, что обусловлено его микросостоянием. Эта энергия называется внутренней (обозначается U). Она равна энергии всех микрочастиц вещества, из которых состоит данное тело. Например, внутренняя энергия идеального газа состоит из кинетической энергии всех его молекул, без учета их потенциальной энергии, поскольку взаимодействием молекул в модели идеального газа пренебрегают.
Модель идеального газа предусматривает, что молекулы пребывают на расстоянии нескольких диаметров друг от друга. Поэтому энергия их взаимодействия намного меньше энергии их движения, следовательно, ею можно пренебречь.
В реальных газах, а также в жидкостях и твердых телах внутреннюю энергию необходимо учитывать, потому что она соизмерима с кинетической энергией и существенно влияет на их свойства. В таком случае их внутренняя энергия состоит из кинетической энергии теплового движения микрочастиц и потенциальной энергии их взаимодействия.
Для того чтобы изменить внутреннюю энергию тела, следует фактически изменить или кинетическую энергию теплового движения микрочастиц, или потенциальную энергию их взаимодействия, или и ту и другую вместе. Многовековой опыт человечества убеждает нас в том, что это можно сделать двумя способами — либо в процессе теплообмена, либо в ходе выполнения работы. В первом случае это произойдет вследствие передачи определенного количества теплоты Q; во втором — в результате выполнения работы А.
Изменение внутренней энергии тела может произойти за счет теплообмена или в результате выполнения работы:
Следовательно, передача количества теплоты и выполнение работы являются факторами, благодаря которым можно изменить внутреннюю энергию тела:
В случае, когда происходит лишь теплообмен, полученное или отданное телом количество теплоты полностью идет на изменение его внутренней энергии, в частности кинетической энергии его атомов и молекул: 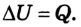
В процессе плавления или кристаллизации твердых тел внутренняя энергия изменяется за счет потенциальной энергии взаимодействия микрочастиц, потому что происходит структурная перестройка вещества. В данном случае изменение внутренней энергии равно теплоте плавления (кристаллизации) тела:
где 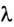
Если изменение внутренней энергии тела происходит вследствие теплообмена, то 
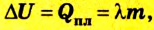
Испарение жидкости или конденсация пара также ведет к изменению внутренней энергии, которая равна в таком случае теплоте парообразования: 
где r — удельная теплота парообразования (конденсации) жидкости.
Изменение внутренней энергии тела вследствие выполнения механической работы (без теплообмена) равно значению работы:
Следовательно, с точки зрения молекулярной физики внутренняя энергия тела является суммой кинетической энергии теплового движения атомов, молекул и других частиц, из которых оно состоит, и потенциальной энергии их взаимодействия. Это энергия термодинамической системы, которая зависит от ее внутреннего состояния. Поэтому вычисляют изменение внутренней энергии 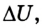
Работа газа
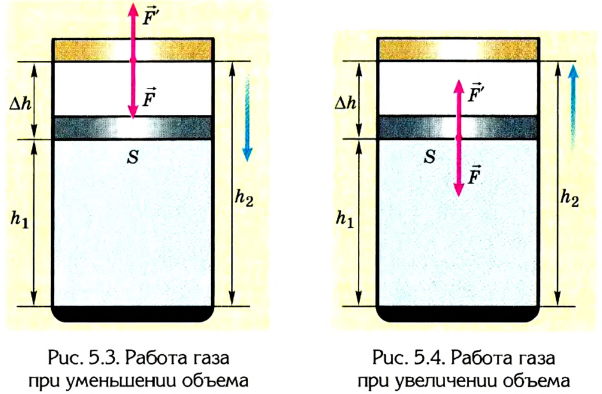
Вычисление выполненной работы в термодинамике связывают с макропараметрами системы. Рассмотрим газ, находящийся в цилиндре под поршнем площадью S (рис. 5.3).
Пусть на газ действует поршень, вызывая его сжатие. Под действием силы F поршень опускается на высоту 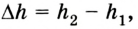
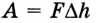
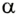
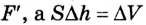
Поскольку 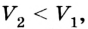
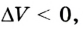
Если под действием силы давления F’ газ расширяется (рис. 5.4), т. е. он сам выполняет работу 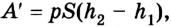
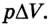
Во время незначительных изменений объема и при постоянном давлении формулы (1) и (2) справедливы не только для газов, но и иных термодинамических систем. Поскольку изменение объема при постоянном давлении сопровождается изменением температуры тела, то можно сделать вывод, что выполнение работы в термодинамике вызывает изменение состояния тела, ведь при этом изменяются его температура Т и объем V.
Видео:Урок 112 (осн). Уравнение теплового балансаСкачать

Первый закон термодинамики
Тот факт, что внутреннюю энергию тела можно изменить двумя способами — в результате выполнения работы или за счет теплопередачи, вынуждал ученых искать соотношение между соответствующими величинами. Вначале в 1842 г. немецкий естествоиспытатель Р. Майер теоретически установил, а затем в 1843 г. английский ученый Дж. Джоуль экспериментально измерил эквивалентность значений количества теплоты и работы. В соответствии с полученными результатами ученые сделали обобщения, которые касались сохранения энергии в природе: энергия в природе не возникает из ничего и не пропадает бесследно; она лишь переходит из одного вида в другой.
Позже этот фундаментальный закон природы приобрел логическую форму первого закона термодинамики: переход термодинамической системы из одного состояния в другое характеризуется изменением ее внутренней энергии, равной сумме работы внешних сил и количества теплоты, переданной системе:
В каком бы состоянии не было тело, оно обладает определенной внутренней энергией. Однако нельзя утверждать, что оно содержит определенное количество теплоты либо запас выполненной работы. Независимо от того, каким из этих способов произведено изменение состояния тела, его состояние однозначно определяется внутренней энергией. Например, газ может быть нагрет за счет передачи ему некоторого количества теплоты либо в результате выполнения внешними силами над ним работы (сжатие газа). Однако невозможно однозначно указать, благодаря какому из этих процессов — выполнению работы или теплопередаче — произошло нагревание газа.
Если система сама выполняет работу (А = -А’), то первый закон термодинамики приобретает другой вид:
т. е. передача термодинамической системе определенного количества теплоты вызывает изменение ее внутренней энергии или выполнение работы, либо то и другое одновременно.
Еще в 1775 г. Французская академия наук приняла решение не рассматривать проекты вечных двигателей.
Последняя формулировка первого закона термодинамики важна с точки зрения отрицания возможности создания вечного двигателя: нельзя создать машину, которая бы неограниченно выполняла работу, не получая энергию извне. Ведь, если количество теплоты Q = 0, то А’ = 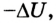
Тепловые двигатели
Человечество научилось использовать тепловую энергию, создав тепловые машины и двигатели. В основу их действия положена идея, что выполнение механической работы может осуществляться за счет теплоты, получаемой от какого-либо нагревателя и частично отдаваемой холодильнику.
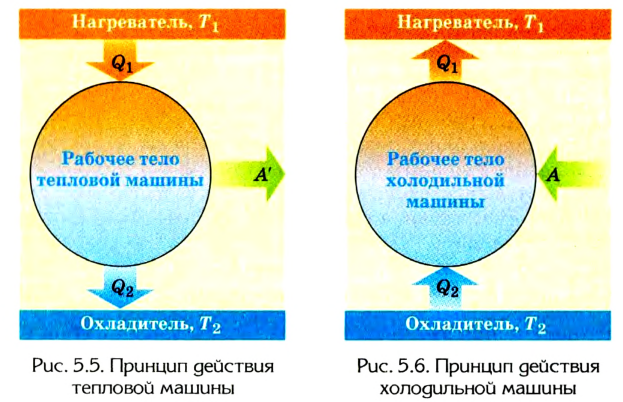
Принцип действия тепловой машины можно представить схематически (рис. 5.5). Нагреватель передает рабочему телу определенное количество теплоты 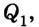
может быть газ или пар, выполняющие работу вследствие своего расширения при нагревании. В паровых турбинах это происходит благодаря паровым котлам, в двигателях внутреннего сгорания — в результате сгорания топливной смеси, в реактивных двигателях — за счет большой теплоотдачи топлива во время быстрого его сгорания.
Выполняя работу, рабочее тело отдает определенную часть количества теплоты 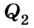
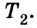
Согласно закону сохранения энергии значение выполненной работы 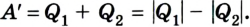
Следовательно, коэффициент полезного действия тепловой машины всегда меньше 1 (часто его представляют в процентах). К примеру, у двигателей внутреннего сгорания он равен приблизительно 44 %, у паровых турбин — до 40 %.
Коэффициент полезного действия равен отношению величины выполненной работы к затраченной при этом энергии:
Холодильник также является тепловой машиной. Принцип его действия основан на обратимости цикла тепловой машины. Холодильная машина работает как тепловой насос: она отбирает тепловую энергию у менее нагретого тела и передает ее более нагретому (рис. 5.6). Это не противоречит законам термодинамики, поскольку охлаждение происходит за счет выполнения работы.
Для того чтобы привести в действие холодильную машину, необходимо над рабочим телом выполнить работу. В таком случае нагревателю будет передаваться количество теплоты, превышающее по значению то, которое отбирается у охладителя: 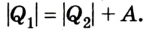
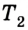
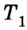
Эффективность работы холодильной машины характеризуется отношением количества теплоты 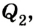
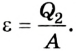
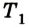
Основные определения и формулы
В основу термодинамического подхода положено описание термодинамической системы при помощи легко измеримых макропараметров — температуры (Т), давления (р), объема (V), массы (m) и др.
Внутренняя энергия тела равна энергии всех микрочастиц вещества, из которых оно состоит. Ее можно изменить за счет теплообмена или в результате выполнения работы. Количество теплоты, переданное телу (либо отобранное у него), определяется в зависимости от теплового процесса, который при этом осуществляется:
при нагревании (охлаждении )
при плавлении (кристаллизации )
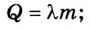
при парообразовании (конденсации)
Работа газа при постоянном давлении (р = const) равна: 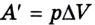
Первый закон термодинамики устанавливает, что количество теплоты, переданное термодинамической системе, вызывает изменение ее внутренней энергии или выполнение работы, либо и той другое одновременно:
Он отражает сущность фундаментального закона сохранения энергии, которым отрицается возможность создания вечного двигателя: нельзя создать машину, которая неограниченно выполняла бы работу, не получая энергию извне.
Законы термодинамики получили широкое практическое применение, в частности, в технике, при конструировании тепловых машин. Все тепловые машины (двигатели внутреннего сгорания, реактивные двигатели, паровые и газовые турбины, холодильные машины и пр.) построены по принципу выполнения механической работы за счет внутренней энергии. Их КПД всегда меньше 1 и равен:
Видео:ЭТОТ метод поможет на уроках ХИМИИ / Химия 9 классСкачать

Основы термодинамики
В 9 классе вы узнали, что полная энергия физической системы представляет собой сумму её механической энергии и внутренних энергий тел, образующих систему. Причём изменение механической энергии в ряде случаев происходит в результате перехода её части во внутреннюю энергию тел системы. Режущие инструменты заметно нагреваются при заточке их на точильном камне. При скольжении конькобежца по льду под коньками тает лёд, что обеспечивает хорошее скольжение. В этих примерах тела при трении нагреваются, и интенсивность хаотического движения молекул возрастает, что приводит к увеличению внутренней энергии тел. Как же определить внутреннюю энергию термодинамической системы? И что понимают под термодинамической системой?
Выводы термодинамики основаны на фундаментальных законах, называемых началами термодинамики. Эти законы установлены в результате обобщения многочисленных экспериментальных фактов. Опираясь на них, термодинамика позволяет делать определённые выводы о свойствах исследуемых систем, которые подтверждаются экспериментально. Физические тела и их модели в термодинамике называют термодинамическими системами. Термодинамическую систему характеризуют набором параметров, определяющих её состояние. В отличие от молекулярно-кинетической теории в термодинамике не рассматривают микроскопическое строение тел и для их описания используют не физические характеристики молекул (микропараметры), а параметры системы (макропараметры), такие как давление, объём, температура.
Замкнутая, или же изолированная, термодинамическая система стремится к равновесию, когда все её макропараметры не изменяются с течением времени. Иначе говоря, для каждой изолированной термодинамической системы существует состояние термодинамического равновесия, в которое она переходит самопроизвольно.
Это утверждение называют нулевым началом термодинамики.
Говоря о полной энергии макроскопического тела, необходимо всегда учитывать не только его механическую энергию (кинетическую и потенциальную), но также кинетическую энергию теплового движения его частиц и потенциальную энергию их взаимодействия. В термодинамике под внутренней энергией тела понимают полную энергию, относящуюся к самим частицам, образующим тело. Это кинетическая энергия теплового движения молекул, кинетическая энергия движения атомов внутри молекул, потенциальная энергия взаимодействия между молекулами, энергия электронных оболочек атомов и внутриядерная энергия.
Внутренняя энергия любой термодинамической системы состоит из внутренних энергий тел, входящих в данную систему.
В термодинамике главную роль играет не сама внутренняя энергия, а её изменение, которое происходит при переходе системы из одного состояния в другое. Под приращением (изменением) внутренней энергии понимают разность внутренних энергий в конечном и начальном состояниях:
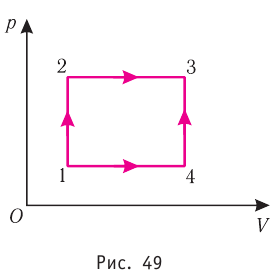
Например, переход некоторой массы идеального газа из состояния / в состояние 3 (рис. 49) можно осуществить или в ходе процесса 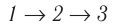
Внутренняя энергия является функцией состояния системы. Это означает, что изменение внутренней энергии при переходе термодинамической системы из одного состояния в другое зависит только лишь от значений параметров этих состояний, а не от процесса перехода.
Внутренняя энергия идеального одноатомного газа:
Определим внутреннюю энергию идеального одноатомного газа, т. е. газа, состоящего из отдельных атомов. Например, к одноатомным газам относят инертные газы — гелий, неон, аргон и др.
Из определения понятия «идеальный газ» следует, что его внутренняя энергия является суммой кинетических энергий хаотического движения всех молекул или атомов (взаимодействие между частицами отсутствует). Следовательно, внутренняя энергия идеального одноатомного газа равна произведению средней кинетической энергии 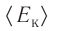
т. е. 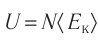
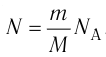
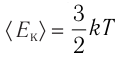
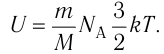
С учётом того, что 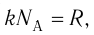
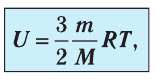
или
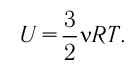
Как видно из формулы (9.1), внутренняя энергия данной массы идеального одноатомного газа пропорциональна абсолютной температуре газа. Она не зависит от других макроскопических параметров состояния — давления и объёма. Следовательно, изменение внутренней энергии данной массы идеального одноатомного газа происходит только при изменении его температуры: 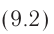
При определении внутренней энергии реальных газов, жидкостей и твёрдых тел необходимо учитывать потенциальную энергию взаимодействия частиц, которая зависит от расстояния между ними. Поэтому в общем случае внутренняя энергия макроскопических тел зависит не только от абсолютной температуры, но и от объёма.
При изучении физики в 8 классе вы узнали, что изменить состояние термодинамической системы можно двумя способами: используя теплопередачу и совершая работу. Процесс теплопередачи и совершение работы характеризуют соответственно физическими величинами — количеством теплоты Q и работой А, которые являются мерами изменения внутренней энергии системы.
- Физические тела и их модели в термодинамике называют термодинамическими системами. Термодинамическую систему характеризуют набором макронараметров, определяющих её состояние.
- Состояние изолированной термодинамической системы, когда все её макропараметры не изменяются с течением времени, называют равновесным.
- Под внутренней энергией термодинамической системы понимают сумму кинетической энергии всех частиц системы и потенциальной энергии их взаимодействия.
- Изменение внутренней энергии тела при переходе из одного состояния в другое зависит только лишь от значений параметров этих состояний, а не от процесса перехода.
- Внутренняя энергия данной массы идеального одноатомного газа зависит только от температуры:
Пример решения задачи №2
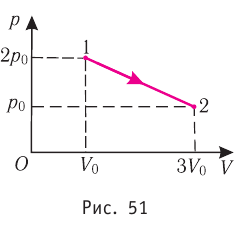
На рисунке 51 в координатах (р, V) изображён процесс перехода идеального одноатомного газа определённой массы из состояния 1 в состояние 2. Определите приращение внутренней энергии газа, если давление газа в конечном состоянии 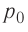
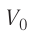
Приращение внутренней энергии идеального одноатомного газа 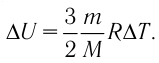
изменение температуры 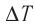
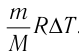
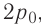
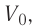
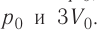
Вычтем из уравнения (2) уравнение (1): 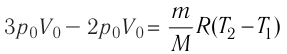
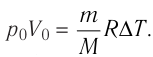
Ответ:
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Необратимость тепловых процессов
- Адиабатический процесс
- Молекулярно-кинетическая теория
- Работа в термодинамике
- Освоение космоса — история, этапы и достижения с фотографиями
- Закон сохранения механической энергии в физике
- Релятивистская механика в физике
- Теория относительности Эйнштейна
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Учимся составлять электронный баланс/овр/8классСкачать
Уравнение энергетического баланса термодинамической системы
Мы уже говорили, что энтропия и энтальпия описывают преобразование энергии. Есть всего два варианта её превращения: энергия может перейти в тепло или в работу. Так вот, энтальпия — это та часть энергии, которая во время химической реакции переходит в тепло. Впервые описание этого процесса предложил американский физикохимик Джозайя Уиллард Гиббс в 1876 году в научной работе «О равновесии гетерогенных веществ» — но тогда он называл её «тепловой функцией при постоянном давлении». Сам термин «энтальпия» предложил голландский физик и химик Хейке Камерлинг-Оннес в 1909 году.
Как же вычисляется энтальпия? Итак, вся энергия, которой вещества обмениваются между собой или с окружающей средой, хранится в связях между составляющими их атомами. Узнать значение энергии в каждой конкретной связи в произвольный момент времени невозможно — все вещества разные, атомы по-разному взаимодействуют между собой, оборот энергии в них тоже разный. И даже если бы мы остановились только на одном типе связи, это было бы сродни вычислению объёма океана в момент, когда в него по литру вливают воду. Гораздо проще вычислить изменение его объёма — оно будет равно тому объёму воды, который в океан добавили. Так же поступают и с энергией. Вместо того, чтобы считать абсолютную энтальпию в каждый момент времени, находят разницу между температурой вещества до вступления в связь с другим веществом и температурой после.
Это имеет большое практическое значение в химии — так предсказывается тепловой эффект химических реакций. Причём в современном мире расчёт теплового эффекта значительно упростился по сравнению с началом XX века: данных о том, сколько тепла выделяется и когда, очень много, и все они сведены в таблицы. Поэтому в процессе работы уже необязательно применять сложные формулы и пользоваться калориметром, чтобы понять, сколько тепла выделится. Достаточно заглянуть в справочную таблицу. Это экономит и время, и реактивы.
Энтальпия характеризует стремление системы — например, системы реагирующих в пробирке веществ — перейти в состояние с наименьшей энергией. Если в процессе химического опыта энергии вырабатывается больше, чем поглощается, то выделяется тепло, а энтальпия убывает. Такая реакция называется экзотермической (от др.-греч. exo — внешний). Если энергии выделяется меньше, чем поглощается, то тепло поглощается — идёт эндотермическая реакция (от др.-греч. endon — внутренний). В этом случае энтальпия возрастает.
Без понимания, какой будет энтальпия (то есть тепловой эффект реакции), сложно принимать решения в химической лаборатории. Нужно ли надевать специальные защитные перчатки? Пользоваться ли термостойкой посудой? А самое главное — нужно ли дополнительно нагревать пробирку для того, чтобы реакция пошла?
Энтальпийный и энтропийный факторы химической реакции действуют независимо друг от друга и могут направлять процесс в противоположные стороны. Джозайя Уиллард Гиббс в своё время не только познакомил научный мир с таким явлением, как энтальпия, — он предложил подход, при котором можно учесть оба фактора и вычислить максимум энергии, способной превратиться в полезную работу. Такую энергию называют свободной энергией Гиббса. Её изменение вычисляется по формуле:
По тому, как изменяется энергия Гиббса, можно отследить, когда реакция происходит самопроизвольно, а когда для её продолжения требуется вмешательство извне. Это важно для любого процесса — будь то промышленное производство или синтез в лаборатории.
Для наглядности приведём бытовой пример — походную грелку для рук. Чтобы сделать такую грелку, нужно подобрать реакцию, которая будет протекать сама по себе, но после небольшого нагревания — растирания грелки руками. При этом от грелки не должно исходить слишком много тепла, иначе можно обжечь руки, но его и не должно быть слишком мало — руки не согреются. Оптимальную температуру можно рассчитать, зная энтальпию и энтропию реакции.
Предлагаем вам следующую задачку. Возьмём два вещества, которые реагируют друг с другом не в растворе, а в твёрдом состоянии и не ядовиты. Их можно поместить в нашу грелку.
Нам нужно выяснить следующее:
- Выделяется ли тепло в результате реакции — будет ли наша грелка греть?
- Будет ли процесс самопроизвольным?
В качестве реагентов возьмём кристаллогидрат гидроокиси бария и хлорид аммония. Наш процесс описывается уравнением реакции:
А теперь подведём итоги. Изменение энтальпии положительное, а значит, в продуктах суммарная энергия больше, чем в реагентах. Следовательно, реакция эндотермическая, то есть протекает с поглощением тепла. Отрицательная энергия Гиббса означает, что процесс самопроизвольный, то есть для протекания этого процесса воздействие извне не нужно. Хоть процесс и самопроизвольный, такая грелка непригодна. Причина в тепловом эффекте реакции: тепло не выделяется, а поглощается, и, следовательно, грелка не греет, а охлаждает!
🎥 Видео
ЕГЭ физика. Уравнение теплового баланса (термодинамика)Скачать

ФИЗИКА ЗА 5 МИНУТ - ТЕРМОДИНАМИКАСкачать

Закон БернуллиСкачать

Химия | Тепловой эффект химической реакции (энтальпия)Скачать

8 класс. ОВР. Окислительно-восстановительные реакции.Скачать

Энергетические уровни. 8 класс.Скачать

Законы Термодинамики. Что Такое Термодинамика?Скачать

Тепловой эффект хим. реакции. Энтальпия. Закон Гесса. Капучинка ^-^Скачать

Урок 176. Задачи на уравнение теплового балансаСкачать

Закон сохранения превращения энергии в тепловых процессах. 8 класс.Скачать

БЕЗ ЭТОГО НЕ СДАТЬ ЕГЭ по Химии — Электронная конфигурация атомаСкачать

Урок 166. Предмет термодинамики. Внутренняя энергия телаСкачать

Как из хаоса рождается порядок? [Veritasium]Скачать
![Как из хаоса рождается порядок? [Veritasium]](https://i.ytimg.com/vi/HmmYtopGx7Y/0.jpg)
Теплообмен. Уравнение теплового баланса 8-10 класс | Физика TutorOnlineСкачать

Как выучить Химию с нуля за 10 минут? Принцип Ле-ШательеСкачать









































































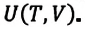
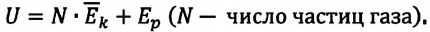
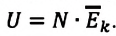
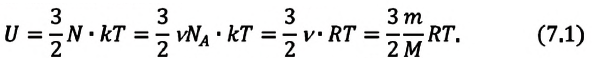

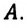

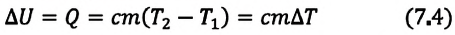


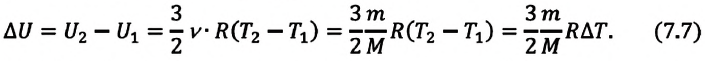
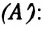

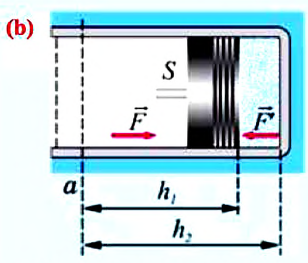
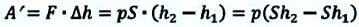

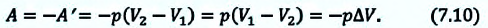
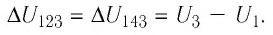
 — приращение физической величины, т. е. разность между её конечным и начальным значениями;
— приращение физической величины, т. е. разность между её конечным и начальным значениями;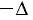 — убыль величины, т. е. разность между её начальным и конечным значениями.
— убыль величины, т. е. разность между её начальным и конечным значениями.