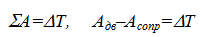Уравнение энергетического баланса тепловой машины (7 видео)

iSopromat.ru

Уравнением энергетического баланса машины называют уравнение, получаемое алгебраической суммой работ всех сил и моментов, действующих на систему, равную приращению кинетической энергии этой системы.

Поэтому при изучении движения машинного агрегата используют теорему об изменении кинетической энергии системы.

В зависимости от приращения кинетической энергии ΔТ выделяют три этапа работы машины:

ΔТ>0 – разбег или разгон машины
ΔТ=0 – этап установившегося движения
ΔТ
Курсовой проект по ТММ >

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Содержание

Тепловые машины
Тепловые двигатели
Холодильные машины
Тепловая машина Карно
Тепловые двигатели и охрана окружающей среды
Тепловое равновесие и уравнение теплового баланса
Что такое теплообмен и при каких условиях он происходит
Уравнение теплового баланса и сохранение тепловой энергии
Уравнение теплового баланса
Если несколько тел участвуют в процессе теплообмена
Пример расчетов для теплообмена между холодным и горячим телом
Задача для самостоятельного решения:
🔍 Видео

Видео:Урок 113 (осн). Задачи на уравнение теплового балансаСкачать

Тепловые машины

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: принципы действия тепловых машин, КПД тепловой машины, тепловые двигатели и охрана окружающей среды.

Коротко говоря, тепловые машины преобразуют теплоту в работу или, наоборот, работу в теплоту.
Тепловые машины бывают двух видов — в зависимости от направления протекающих в них процессов.

1. Тепловые двигатели преобразуют теплоту, поступающую от внешнего источника, в механическую работу.

2. Холодильные машины передают тепло от менее нагретого тела к более нагретому за счёт механической работы внешнего источника.

Рассмотрим эти виды тепловых машин более подробно.

Видео:Урок 112 (осн). Уравнение теплового балансаСкачать

Тепловые двигатели

Мы знаем, что совершение над телом работы есть один из способов изменения его внутренней энергии: совершённая работа как бы растворяется в теле, переходя в энергию беспорядочного движения и взаимодействия его частиц.

Рис. 1. Тепловой двигатель

Тепловой двигатель — это устройство, которое, наоборот, извлекает полезную работу из «хаотической» внутренней энергии тела. Изобретение теплового двигателя радикально изменило облик человеческой цивилизации.

Принципиальную схему теплового двигателя можно изобразить следующим образом (рис. 1 ). Давайте разбираться, что означают элементы данной схемы.

Рабочее тело двигателя — это газ. Он расширяется, двигает поршень и совершает тем самым полезную механическую работу.

Но чтобы заставить газ расширяться, преодолевая внешние силы, нужно нагреть его до температуры, которая существенно выше температуры окружающей среды. Для этого газ приводится в контакт с нагревателем — сгорающим топливом.

В процессе сгорания топлива выделяется значительная энергия, часть которой идёт на нагревание газа. Газ получает от нагревателя количество теплоты . Именно за счёт этого тепла двигатель совершает полезную работу .

Это всё понятно. Что такое холодильник и зачем он нужен?

При однократном расширении газа мы можем использовать поступающее тепло максимально эффективно и целиком превратить его в работу. Для этого надо расширять газ изотермически: первый закон термодинамики, как мы знаем, даёт нам в этом случае .

Но однократное расширение никому не нужно. Двигатель должен работать циклически, обеспечивая периодическую повторяемость движений поршня. Следовательно, по окончании расширения газ нужно сжимать, возвращая его в исходное состояние.

В процессе расширения газ совершает некоторую положительную работу . В процессе сжатия над газом совершается положительная работа (а сам газ совершает отрицательную работу ). В итоге полезная работа газа за цикл: .

Разумеется, должно быть 0′ alt=’A>0′ /> , или (иначе никакого смысла в двигателе нет).

Сжимая газ, мы должны совершить меньшую работу, чем совершил газ при расширении.

Как этого достичь? Ответ: сжимать газ под меньшими давлениями, чем были в ходе расширения. Иными словами, на -диаграмме процесс сжатия должен идти ниже процесса расширения, т. е. цикл должен проходиться по часовой стрелке (рис. 2 ).

Рис. 2. Цикл теплового двигателя

Например, в цикле на рисунке работа газа при расширении равна площади криволинейной трапеции . Аналогично, работа газа при сжатии равна площади криволинейной трапеции со знаком минус. В результате работа газа за цикл оказывается положительной и равной площади цикла .

Хорошо, но как заставить газ возвращаться в исходное состояние по более низкой кривой, т. е. через состояния с меньшими давлениями? Вспомним, что при данном объёме давление газа тем меньше, чем ниже температура. Стало быть, при сжатии газ должен проходить состояния с меньшими температурами.

Вот именно для этого и нужен холодильник: чтобы охлаждать газ в процессе сжатия.

Холодильником может служить атмосфера (для двигателей внутреннего сгорания) или охлаждающая проточная вода (для паровых турбин). При охлаждении газ отдаёт холодильнику некоторое количество теплоты .

Суммарное количество теплоты, полученное газом за цикл, оказывается равным . Согласно первому закону термодинамики:

где — изменение внутренней энергии газа за цикл. Оно равно нулю: , так как газ вернулся в исходное состояние (а внутренняя энергия, как мы помним, является функцией состояния). В итоге работа газа за цикл получается равна:

Как видите, : не удаётся полностью превратить в работу поступающее от нагревателя тепло. Часть теплоты приходится отдавать холодильнику — для обеспечения цикличности процесса.

Показателем эффективности превращения энергии сгорающего топлива в механическую работу служит коэффициент полезного действия теплового двигателя.

КПД теплового двигателя — это отношение механической работы к количеству теплоты , поступившему от нагревателя:

С учётом соотношения (1) имеем также

КПД теплового двигателя, как видим, всегда меньше единицы. Например, КПД паровых турбин приблизительно , а КПД двигателей внутреннего сгорания около .

Видео:ЕГЭ физика. Уравнение теплового баланса (термодинамика)Скачать

Холодильные машины

Житейский опыт и физические эксперименты говорят нам о том, что в процессе теплообмена теплота передаётся от более нагретого тела к менее нагретому, но не наоборот. Никогда не наблюдаются процессы, в которых за счёт теплообмена энергия самопроизвольно переходит от холодного тела к горячему, в результате чего холодное тело ещё больше остывало бы, а горячее тело — ещё больше нагревалось.

Рис. 3. Холодильная машина

Ключевое слово здесь — «самопроизвольно». Если использовать внешний источник энергии, то осуществить процесс передачи тепла от холодного тела к горячему оказывается вполне возможным. Это и делают холодильные
машины.

По сравнению с тепловым двигателем процессы в холодильной машине имеют противоположное направление (рис. 3 ).

Рабочее тело холодильной машины называют также хладагентом. Мы для простоты будем считать его газом, который поглощает теплоту при расширении и отдаёт при сжатии (в реальных холодильных установках хладагент — это летучий раствор с низкой температурой кипения, который забирает теплоту в процессе испарения и отдаёт при конденсации).

Холодильник в холодильной машине — это тело, от которого отводится теплота. Холодильник передаёт рабочему телу (газу) количество теплоты , в результате чего газ расширяется.

В ходе сжатия газ отдаёт теплоту более нагретому телу — нагревателю. Чтобы такая теплопередача осуществлялась, надо сжимать газ при более высоких температурах, чем были при расширении. Это возможно лишь за счёт работы , совершаемой внешним источником (например, электродвигателем (в реальных холодильных агрегатах электродвигатель создаёт в испарителе низкое давление, в результате чего хладагент вскипает и забирает тепло; наоборот, в конденсаторе электродвигатель создаёт высокое давление, под которым хладагент конденсируется и отдаёт тепло)). Поэтому количество теплоты, передаваемое нагревателю, оказывается больше количества теплоты, забираемого от холодильника, как раз на величину :

Таким образом, на -диаграмме рабочий цикл холодильной машины идёт против часовой стрелки. Площадь цикла — это работа , совершаемая внешним источником (рис. 4 ).

Рис. 4. Цикл холодильной машины

Основное назначение холодильной машины — охлаждение некоторого резервуара (например, морозильной камеры). В таком случае данный резервуар играет роль холодильника, а нагревателем служит окружающая среда — в неё рассеивается отводимое от резервуара тепло.

Показателем эффективности работы холодильной машины является холодильный коэффициент, равный отношению отведённого от холодильника тепла к работе внешнего источника:

Холодильный коэффициент может быть и больше единицы. В реальных холодильниках он принимает значения приблизительно от 1 до 3.

Имеется ещё одно интересное применение: холодильная машина может работать как тепловой насос. Тогда её назначение — нагревание некоторого резервуара (например, обогрев помещения) за счёт тепла, отводимого от окружающей среды. В данном случае этот резервуар будет нагревателем, а окружающая среда — холодильником.

Показателем эффективности работы теплового насоса служит отопительный коэффициент, равный отношению количества теплоты, переданного обогреваемому резервуару, к работе внешнего источника:

Значения отопительного коэффициента реальных тепловых насосов находятся обычно в диапазоне от 3 до 5.

Видео:Энергия топлива, удельная теплота сгорания топлива. 8 класс.Скачать

Тепловая машина Карно

Важными характеристиками тепловой машины являются наибольшее и наименьшее значения температуры рабочего тела в ходе цикла. Эти значения называются соответственно температурой нагревателя и температурой холодильника.

Мы видели, что КПД теплового двигателя строго меньше единицы. Возникает естественный вопрос: каков наибольший возможный КПД теплового двигателя с фиксированными значениями температуры нагревателя и температуры холодильника ?

Пусть, например, максимальная температура рабочего тела двигателя равна , а минимальная — . Каков теоретический предел КПД такого двигателя?

Ответ на поставленный вопрос дал французский физик и инженер Сади Карно в 1824 году.

Он придумал и исследовал замечательную тепловую машину с идеальным газом в качестве рабочего тела. Эта машина работает по циклу Карно, состоящему из двух изотерм и двух адиабат.

Рассмотрим прямой цикл машины Карно, идущий по часовой стрелке (рис. 5 ). В этом случае машина функционирует как тепловой двигатель.

Рис. 5. Цикл Карно

Изотерма . На участке газ приводится в тепловой контакт с нагревателем температуры и расширяется изотермически. От нагревателя поступает количество теплоты и целиком превращается в работу на этом участке: .

Адиабата . В целях последующего сжатия нужно перевести газ в зону более низких температур. Для этого газ теплоизолируется, а затем расширяется адиабатно на учатке .

При расширении газ совершает положительную работу , и за счёт этого уменьшается его внутренняя энергия: .

Изотерма . Теплоизоляция снимается, газ приводится в тепловой контакт с холодильником температуры . Происходит изотермическое сжатие. Газ отдаёт холодильнику количество теплоты и совершает отрицательную работу .

Адиабата . Этот участок необходим для возврата газа в исходное состояние. В ходе адиабатного сжатия газ совершает отрицательную работу , а изменение внутренней энергии положительно: . Газ нагревается до исходной температуры .

Карно нашёл КПД этого цикла (вычисления, к сожалению, выходят за рамки школьной программы):

Кроме того, он доказал, что КПД цикла Карно является максимально возможным для всех тепловых двигателей с температурой нагревателя и температурой холодильника .

Так, в приведённом выше примере имеем:

В чём смысл использования именно изотерм и адиабат, а не каких-то других процессов?

Оказывается, изотермические и адиабатные процессы делают машину Карно обратимой. Её можно запустить по обратному циклу (против часовой стрелки) между теми же нагревателем и холодильником, не привлекая другие устройства. В таком случае машина Карно будет функционировать как холодильная машина.

Возможность запуска машины Карно в обоих направлениях играет очень большую роль в термодинамике. Например, данный факт служит звеном доказательства максимальности КПД цикла Карно. Мы ещё вернёмся к этому в следующей статье, посвящённой второму закону термодинамики.

Видео:89 НЕ ЗНАЮТ этого в Физике: Что такое Количество Теплоты, Теплоемкость, Уравнение Теплового БалансаСкачать

Тепловые двигатели и охрана окружающей среды

Тепловые двигатели наносят серьёзный ущерб окружающей среде. Их повсеместное использование приводит к целому ряду негативных эффектов.

• Рассеяние в атмосферу огромного количества тепловой энергии приводит к повышению температуры на планете. Потепление климата грозит обернуться таянием ледников и катастрофическими бедствиями.
• К потеплению климата ведёт также накопление в атмосфере углекислого газа, который замедляет уход теплового излучения Земли в космос (парниковый эффект).
• Из-за высокой концентрации продуктов сгорания топлива ухудшается экологическая ситуация.

Это — проблемы в масштабе всей цивилизации. Для борьбы с вредными последствиями работы тепловых двигателей следует повышать их КПД, снижать выбросы токсичных веществ, разрабатывать новые виды топлива и экономно расходовать энергию.

Видео:Уравнение теплового балансаСкачать

Тепловое равновесие и уравнение теплового баланса

Тела, температура которых отличается, могут обмениваться тепловой энергией. То есть, между телами будет происходить теплообмен. Самостоятельно тепловая энергия переходит от более нагретых тел к менее нагретым.

Видео:Решение задач на уравнение теплового баланса. Физика 8 классСкачать

Что такое теплообмен и при каких условиях он происходит

Тела, имеющие различные температуры, будут обмениваться тепловой энергией. Этот процесс называется теплообменом.

Теплообмен – процесс обмена тепловой энергией между телами, имеющими различные температуры.

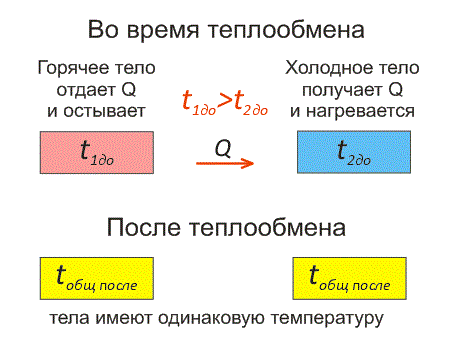
Рассмотрим два тела, имеющие различные температуры (рис. 1).

Тело, имеющее более высокую температуру, будет остывать и отдавать тепловую энергию телу, имеющему низкую температуру. А тело с низкой температурой будет получать количество теплоты и нагреваться.

На рисунке, горячее тело имеет розовый оттенок, а холодное изображено голубым цветом.

Когда температуры тел выравниваются, теплообмен прекращается.

Чтобы теплообмен происходил, нужно, чтобы тела имели различные температуры.

Когда температура тел выравняется, теплообмен прекратится.

Тепловое равновесие — это состояние, при котором тела имеют одинаковую температуру.

Видео:Процессы и аппараты. Материальный балансСкачать

Уравнение теплового баланса и сохранение тепловой энергии

Когда тело остывает, оно отдает тепловую энергию (теплоту). Утерянное количество теплоты Q имеет знак «минус».

А когда тело нагревается – оно получает тепловую энергию. Приобретенное количество теплоты Q имеет знак «плюс».

Эти факты отражены на рисунке 2.

Закон сохранения тепловой энергии: Количество теплоты, отданное горячим телом равно количеству теплоты, полученному холодным телом.

Примечание: Существует и другая формулировка закона сохранения энергии: Энергия не появляется сама собой и не исчезает бесследно. Она переходит из одного вида в другой.

Уравнение теплового баланса

Тот факт, что тепловая энергия сохраняется, можно записать с помощью математики в виде уравнения. Такую запись называют уравнением теплового баланса.

Запишем уравнение теплового баланса для двух тел, обменивающихся тепловой энергией:

(large Q_<text> left( text right) ) – это количество теплоты горячее тело теряет.

(large Q_<text> left( text right) ) – это количество теплоты холодное тело получает.

В левой части уравнения складываем количество теплоты каждого из тел, участвующих в теплообмене.

Записываем ноль в правой части уравнения, когда теплообмен с окружающей средой отсутствует. То есть, теплообмен происходит только между рассматриваемыми телами.

В некоторых учебниках применяют сокращения:

[large Q_ + Q_ = 0 ]

Примечание: Складывая два числа мы получим ноль, когда эти числа будут:

равными по модулю и
имеют различные знаки (одно число — знак «плюс», а второе – знак «минус»).

Если несколько тел участвуют в процессе теплообмена

Иногда в процессе теплообмена участвуют несколько тел. Тогда, для каждого тела нужно записать формулу количества теплоты Q. А потом все количества теплоты подставить в уравнение для теплового баланса:

[large boxed < Q_+ Q_ + Q_ + ldots + Q_ = 0 > ]

Q для каждого нагреваемого тела будет обладать знаком «+»,
Q для каждого охлаждаемого тела — знаком «-».

Видео:Закон сохранения превращения энергии в тепловых процессах. 8 класс.Скачать

Пример расчетов для теплообмена между холодным и горячим телом

К горячей воде, массой 200 грамм, имеющей температуру +80 градусов Цельсия, добавили холодную воду, в количестве 100 грамм при температуре +15 градусов Цельсия. Какую температуру будет иметь смесь после установления теплового равновесия? Считать, что окружающая среда в теплообмене не участвует.

Примечание: Здесь мы рассматриваем упрощенную задачу, для того, чтобы облегчить понимание закона сохранения энергии. Мы не учитываем в этой задаче, что вода содержится в емкости. И часть тепловой энергии будет затрачиваться на то, чтобы изменить температуру емкости.

При решении других задач обязательно учитывайте, что емкость, в которой будет содержаться вещество, имеет массу. И часть тепловой энергии будет затрачиваться на то, чтобы изменить температуру емкости.

Решение:

В условии сказано, что окружающая среда в теплообмене не участвует. Поэтому, будем считать рассматриваемую систему замкнутой. А в замкнутых системах выполняются законы сохранения. Например, закон сохранения энергии.

Иными словами, с сосудом и окружающим воздухом теплообмен не происходит и, все тепловая энергия, отданная горячей водой, будет получена холодной водой.

1). Запишем уравнение теплового баланса, в правой части которого можно записать ноль:

2). Теперь запишем формулу для каждого количества теплоты:

Примечания:

(large c_<text> ) – удельную теплоемкость воды находим в справочнике;
Массу воды переводим в килограммы;
Горячая вода остывает и отдает тепловую энергию. Поэтому, разность (large (t_<text> — t_<text> ) ) будет иметь знак «минус», потому, что конечная температура горячей воды меньше ее начальной температуры;
Холодная вода получает тепловую энергию и нагревается. Из-за этого, разность (large (t_<text> — t_<text> ) ) будет иметь знак «плюс», потому, что конечная температура холодной воды больше ее начальной температуры;

3). Подставим выражения для каждого Q в уравнение баланса:

4). Для удобства, заменим символы числами:

[large 4200 cdot 0,2 cdot (t_<text> — 80 ) + 4200 cdot 0,1 cdot (t_<text> — 15 ) = 0 ]

[large 840 cdot (t_<text> — 80 ) + 420 cdot (t_<text> — 15 ) = 0 ]

Раскрыв скобки и решив это уравнение, получим ответ:

Ответ: Температура смеси после прекращения теплообмена будет равна 58,33 градуса Цельсия.

Задача для самостоятельного решения:

В алюминиевом калориметре массой 100 грамм находится керосин массой 250 грамм при температуре +80 градусов Цельсия. В керосин поместили свинцовый шарик, массой 300 грамм. Начальная температура шарика +20 градусов Цельсия. Найдите температуру тел после установления теплового равновесия. Внешняя среда в теплообмене не участвует.

Примечание к решению: В левой части уравнения теплового баланса теперь будут находиться три слагаемых. Потому, что мы учитываем три количества теплоты:

(large Q_ ) – охлаждение алюминия от температуры +80 градусов до конечной температуры;
(large Q_ ) – охлаждение керосина от температуры +80 градусов до конечной температуры;
(large Q_ ) – нагревание свинца от температуры +20 градусов до конечной температуры;

А справа в уравнение теплового баланса запишем ноль. Так как внешняя среда в теплообмене не участвует.