Уравнение эллипсоида в сферических координатах

$d=sqrt$

НАПРАВЛЯЮЩИЙ КОСИНУС ЛИНИИ, СОЕДИНЯЮЩЕЯ ТОЧКИ $P_1(x_1,y_1,z_1)$ И $P_2(x_2,y_2,z_2)$
$l=cosalpha=frac$, $m=cosbeta=frac$, $n=cosgamma=frac$

где $alpha,beta,gamma$ углы, которые линия $P_1P_2$ образовывает с положительными осями $x,y,z$ соответственно, а $d$ определено на рисунке вверху.

ОТНОШЕНИЕ МЕЖДУ НАПРЯВЛЯЮЩИМИ КОСИНУСАМИ
$cos^2alpha+cos^2beta+cos^2gamma=1$ или $l^2+m^2+n^2=1$

НАПРАВЛЯЮЩИЕ ЧИСЛА
Числа $L,M,N$, которые есть пропорциональны к направляющим косинусам $l, m, n$ называются направляющими числами. Отношение между ними

Это также действительно, если $l, m, n$ заменяются на $L, M, N$ соответственно.

УРАВНЕНИЯ ЛИНИИ, СОЕДИНЯЮЩЕЙ $P_1(x_1,y_1,z_1)$ И $P_2(x_2,y_2,z_2)$ В ПАРАМЕТРИЧЕСКОЙ ФОРМЕ
$x=x_1+lt$, $y=y_1+mt$, $z=z_1+nt$

Это также действительно если $l, m, n$ заменяются на $L, M, N$ соответственно.

УГОЛ $phi$ МЕЖДУ ДВУМЯ ЛИНЯМИ С НАПРАВЛЯЮЩИМИ КОСИНУСАМИ $l_1, m_1, n_1$ И $l_2, m_2, n_2$
$cosphi=l_1l_2+m_1m_2+n_1n_2$

ОБЩЕЕ УРАВНЕНИЕ ПЛОСКОСТИ
$Ax + By + Cz + D = 0$ [$A, B, C, D$ — константы]

УРАВНЕНИЕ ПЛОСКОСТИ, ПРОХОДЯЩЕЙ ЧЕРЕЗ ТОЧКИ $(x_1,y_1,z_1),(x_2,y_2,z_2),(x_3,y_3,z_3)$

$beginx-x_1 & y-y_1 & z-z_1\ x_2-x_1 & y_2-y_1 & z_2-z_1\ x_3-x_1 & y_3-y_1 & z_3-z_1end=0$

$begin y_2-y_1 & z_2-z_1\ y_3-y_1 & z_3-z_1end(x-x_1)$ $+begin z_2-z_1 & x_2-x_1\ z_3-z_1 & x_3-x_1end(y-y_1)$ $+begin x_2-x_1 & y_2-y_1\ x_3-x_1 & y_3-y_1end(z-z_1)=0$

где $a, b, c$ есть пересечения на осях $x, y, z$ соответственно.

Обратите внимание, что направляющие числа для линии, перпендикулярной к плоскости $Ax + By + Cz + D = 0$ есть $A, B, C$.

где знак выбирается так, что расстояние не является отрицательным.

НОРМАЛЬНОЕ УРАВНЕНИЯ ПЛОСКОСТИ
$xcosalpha+ycosbeta+zcosgamma=p$

где $p$ = перпендикулярному расстоянию от $O$ к плоскости в $P$ и $alpha, beta, gamma$ есть углами между $OP$ и положительными осями $x, y, z$.

ПРЕОБРАЗОВАНИЕ КООРДИНАТ ПРИ ПЕРЕМЕЩЕНИИ
$left<beginx=x’+x_0\ y=y’+y_0\ z=z’+z_0endright.$ $left<beginx’=x-x_0\ y’=y-y_0\ z’=z-z_0endright.$

где $(x, y, z)$ — старые координаты [т.e. координаты относительно системы xyz], $(x’, y’, z’)$ — новые координаты [относительно системы $x’y’z’$] и $(x_0,y_0,z_0)$ координаты нового центра $O’$ относительно старой координатной системы $xyz$.

ПРЕОБРАЗОВАНИЕ КООРДИНАТ ПРИ ВРАЩЕНИИ

где центры систем $xyz$ и $x’y’z’$ находятся в одной точке и $l_1,m_1,n_1; l_2,m_2,n_2; l_3,m_3,n_3$ направляющие косинусы осей $x’, y’, z’$ относительно осей $x, y, z$ соответственно.

ПРЕОБРАЗОВАНИЕ КООРДИНАТ ПРИ ПЕРЕМЕЩЕНИИ И ВРАЩЕНИИ

$left<beginx=l_1x’+l_2y’+l_3z’+x_0\ y=m_1x’+m_2y’+m_3z’+y_0\ z=n_1x’+n_2y’+n_3z’+z_0endright.$

$left<beginx’=l_1(x-x_0)+m_1(y-y_0)+n_1(z-z_0)\ y’=l_2(x-x_0)+m_2(y-y_0)+n_2(z-z_0)\ z’=l_3(x-x_0)+m_3(y-y_0)+n_3(z-z_0)endright.$

где $O’$ системы $x’y’z’$ имеет координаты $(x_0,y_0,z_0)$ относительно системы $xyz$ и $l_1,m_1,n_1; l_2,m_2,n_2; l_3,m_3,n_3$ направляющие косинусы осей $x’, y’, z’$ относительно осей $x, y, z$ соответственно.

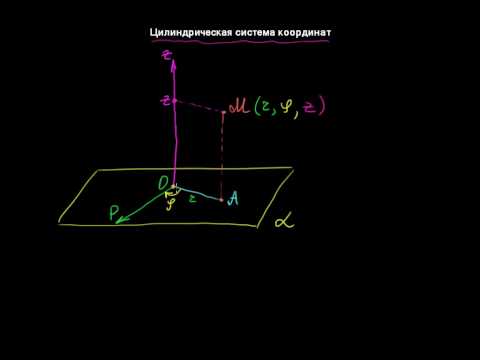
ЦИЛИНДРИЧЕСКИЕ КООРДИНАТЫ $(r, theta, z)$
Точка $P$ может быть определена как цилиндрическими координатами $(r, theta, z)$, так и прямоугольными координатами $(x, y, z)$.
Преобразование между этими двумя координатами есть

СФЕРИЧЕСКИЕ КООРДИНАТЫ $(r, theta, phi)$
Точка $P$ может быть определена как сферическими координатами $(r, theta, phi)$ так и прямоугольными координатами $(x, y, z)$.
Преобразование между этими двумя кординатами есть

$left<beginx=rsinthetacosphi\ y=rsinthetasinphi\ z=rcosthetaendright.$

УРАВНЕНИЕ СФЕРЫ В ПРЯМОУГОЛЬНЫХ КООРДИНАТАХ
$(x-x_0)^2+(y-y_0)^2+(z-z_0)^2=R^2$

где сфера имеет центр $(x_0,y_0,z_0)$ и радиус $R$.

УРАВНЕНИЕ СФЕРЫ В ЦИЛИНДРИЧЕСКИХ КООРДИНАТАХ
$r^2-2r_0r(theta-theta_0)+r_0^2+(z-z_0)^2=R^2$

где сфера имеет центр $(r_0;theta_0;z_0)$ в цилиндрических координатах и радиус $R$.

Если центр находится в начале координат, уравнение имеет вид:

УРАВНЕНИЕ СФЕРЫ В СФЕРИЧЕСКИХ КООРДИНАТАХ
$r^2+r_0^2-2r_0 rsinthetasintheta_0cos(phi-phi_0)=R^2$

где сфера имеет центр $(r_0; theta_0; phi_0)$ в сферических координатах и радиус $R$.

Если центр в начале координат, уравнение имеет вид:

ЭЛЛИПТИЧЕСКИЙ ЦИЛИНДР С ОСЬЮ КАК $z$ ОСЬ
$frac+frac=1$

где $a, b$ — полуоси эллиптического сечения.
Если $b = a$, фигура превращается в цилиндрический цилиндр с радиусом $a$.

Обратите внимание на ориентацию осей этой фигуры.

Видео:Полярные координаты. Полярное уравнение эллипса.Скачать

Эллипсоид: характеристики и примеры

Эллипсоид: характеристики и примеры — Наука

Видео:Сферические координатыСкачать

Содержание:

В эллипсоид — поверхность в пространстве, принадлежащая к группе квадратичных поверхностей, общее уравнение которой имеет вид:

Топор 2 + Автор 2 + Cz 2 + Dxy + Exz + Fyz + Gx + Hy + Iz + J = 0

Это трехмерный эквивалент эллипса, для которого в некоторых особых случаях характерны эллиптические и круговые следы. Следы — это кривые, полученные пересечением эллипсоида плоскостью.

Помимо эллипсоида, есть еще пять квадрик: одностворчатый и двухлистный гиперболоид, два типа параболоида (гиперболический и эллиптический) и эллиптический конус. Его следы также имеют коническую форму.

Эллипсоид также можно выразить стандартным уравнением в декартовых координатах. Эллипсоид с центром в начале координат (0,0,0), выраженный таким образом, напоминает эллипс, но с дополнительным членом:

Ценности к, б Y c являются действительными числами больше 0 и представляют три полуоси эллипсоида.

Видео:§30 Уравнения кривых второго порядка в полярных координатахСкачать

Характеристики эллипсоида

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

— Стандартное уравнение

Стандартное уравнение в декартовых координатах для эллипса с центром в точке (ч, к, м) это:

Видео:§56 Сферическая система координатСкачать

— Параметрические уравнения эллипсоида

В сферических координатах эллипсоид можно описать следующим образом:

х = грех θ. cos φ

у = б грех θ. сен φ

Полуоси эллипсоида остаются a, b и c, а параметрами являются углы θ и φ на следующем рисунке:

Видео:Полярная система координатСкачать

— Следы эллипсоида

Общее уравнение поверхности в пространстве: F (x, y, z) = 0, а следы поверхности — это кривые:

— х = с; F (c, y, z) = 0

— у = с; F (х, с, z) = 0

— z = c; F (х, у, с) = 0

В случае эллипсоида такие кривые представляют собой эллипсы, а иногда и окружности.

Видео:Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

— Объем

Объем V эллипсоида равен (4/3) π умноженным на произведение трех его полуосей:

Видео:Объем через тройной интеграл в сферической системе координатСкачать

Частные случаи эллипсоида

-Эллипсоид становится сферой, когда все полуоси имеют одинаковый размер: a = b = c ≠ 0. Это имеет смысл, поскольку эллипсоид подобен сфере, которая была растянута по-разному вдоль каждой оси. ось.

-Сфероид представляет собой эллипсоид, в котором две полуоси идентичны, а третья другая, например, это может быть a = b ≠ c.

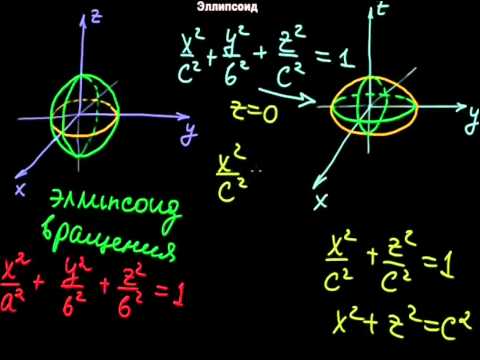
Сфероид также называют эллипсоидом вращения, потому что он может быть образован вращением эллипсов вокруг оси.

Если ось вращения совпадает с большой осью, сфероид имеет вид вытянутый, но если он совпадает с малой осью, он сплюснутый:

Мера уплощения сфероида (эллиптичность) определяется разницей в длине между двумя полуосями, выраженной в дробной форме, то есть это единица сплющивания, определяемая как:

В этом уравнении a представляет большую полуось, а b — малую ось, помните, что третья ось равна одной из них для сфероида. Значение f находится в диапазоне от 0 до 1, а для сфероида оно должно быть больше 0 (если бы оно было равно 0, у нас была бы просто сфера).

Видео:Сферические координаты и координатные линииСкачать

Справочный эллипсоид

Планеты и звезды в целом обычно не являются идеальными сферами, потому что вращательное движение вокруг их осей сглаживает тело на полюсах и выпячивает его на экваторе.

Вот почему Земля похожа на сплюснутый сфероид, хотя и не такой преувеличенный, как на предыдущем рисунке, а газовый гигант Сатурн со своей стороны является самой плоской из планет Солнечной системы.

Таким образом, более реалистичный способ представить планеты — это предположить, что они похожи на сфероид или эллипсоид вращения, большая полуось которого соответствует экваториальному радиусу, а малая полуось — полярному радиусу.

Тщательные измерения, сделанные на земном шаре, позволили построитьопорный эллипсоид Земли как наиболее точный способ математической работы.

Звезды также имеют вращательные движения, которые придают им более или менее уплощенные формы. Быстрая звезда Ахернар, восьмая по яркости звезда на ночном небе, в южном созвездии Эридана, имеет удивительно эллиптическую форму по сравнению с большинством из них. Это 144 световых года от нас.

С другой стороны, несколько лет назад ученые обнаружили самый сферический объект из когда-либо обнаруженных: звезду Кеплер 11145123, находящуюся на расстоянии 5000 световых лет, в два раза больше нашего Солнца и с разницей между полуосями всего в 3 км. Как и ожидалось, он тоже медленнее вращается.

Что касается Земли, то она не является идеальным сфероидом из-за неровной поверхности и местных изменений силы тяжести. По этой причине доступно более одного эталонного сфероида, и на каждом сайте выбирается наиболее подходящий для местной географии.

Помощь спутников неоценима в создании все более точных моделей формы Земли, благодаря которым известно, например, что южный полюс ближе к экватору, чем северный полюс.

Видео:§65 ЭллипсоидСкачать

Числовой пример

Из-за вращения Земли создается центробежная сила, которая придает ей форму продолговатого эллипсоида, а не сферы. Известно, что экваториальный радиус Земли составляет 3963 мили, а полярный радиус — 3942 мили.

Найдите уравнение экваториального следа этого эллипсоида и меру его уплощения. Также сравните с эллиптичностью Сатурна, с данными, приведенными ниже:

Экваториальный радиус Сатурна: 60 ​​268 км

-Полярный радиус Сатурна: 54,364 км

Видео:§55 Цилиндрическая система координатСкачать

Решение

Требуется система координат, центр которой мы будем считать центрированной в начале координат (центре Земли). Предположим, что вертикальная ось z и след, соответствующий экватору, лежит в плоскости xy, эквивалентной плоскости z = 0.

В экваториальной плоскости полуоси a и b равны, поэтому a = b = 3963 мили, а c = 3942 мили. Это особый случай: сфероид с центром в точке (0,0,0), как упоминалось выше.

Экваториальный след представляет собой круг радиусом R = 3963 мили с центром в начале координат. Он рассчитывается путем принятия z = 0 в стандартном уравнении:

А стандартное уравнение земного эллипсоида:

F_Земля = (a — b) / a = (3963-3942) миль / 3963 мили = 0,0053

F _Сатурн = (60268-54363) км / 60268 км = 0,0980

Отметим, что эллиптичность f — безразмерная величина.

Видео:Цилиндрическая система координат(ЦСК).Тройной интегралСкачать

Ссылки

1. ArcGIS for Desktop. Сфероиды и сферы. Получено с: desktop.arcgis.com.
2. BBC World. Тайна самого сферического объекта, когда-либо обнаруженного во Вселенной. Получено с: bbc.com.
3. Ларсон Р. Исчисление и аналитическая геометрия. Издание шестое. Том 2. Макгроу Хилл.
4. Википедия. Эллипсоид. Получено с: en.wikipedia.org.
5. Википедия. Сфероид. Получено с: en.wikipedia.org.

Как мотивировать команду на работе: 8 советов

Призма семиугольная: характеристики, объем, площадь

Видео:Сферическое движениеСкачать

6.3. Эллипсоид

Каноническое уравнение эллипсоида имеет вид , где – положительные числа (полуоси эллипсоида), которые в общем случае различны. Эллипсоидом называют как поверхность, так и тело, ограниченное данной поверхностью. Тело задаётся неравенством и координаты любой внутренней точки (а также любой точки поверхности) обязательно удовлетворяют этому неравенству. Конструкция симметрична относительно координатных осей и координатных плоскостей:

Происхождение термина «эллипсоид» тоже очевидно: если поверхность «разрезать» координатными плоскостями, то в сечениях получатся три различных (в общем случае) эллипса. В зависимости от значений эллипсоид может быть вытянут вдоль любой оси, причём вытянут достаточно далеко.

Если две полуоси совпадают, то данную поверхность / тело называют эллипсоидом вращения. Так, например, эллипсоид получен вращением эллипса вокруг оси (представьте мысленно).

Небольшая задачка для самостоятельного решения:

Задача 173

Построить эллипсоид . Записать уравнение порождающего эллипса и ось, вокруг которой осуществляется его вращение.

Чертеж с комментариями в конце книги.

В случае равенства всех полуосей , эллипсоид вырождается в сферу:
– данное уравнение задаёт сферу с центром в начале координат радиуса .

Тело, ограниченное сферой, называется шаром. Неравенство определяет шар с центром в начале координат радиуса . И, соответственно, противоположному условию удовлетворяют координаты любой внешней точки.

Разделаемся с аппетитным Колобком:

Задача 174

Построить поверхность . Найти функции, задающие верхнюю и нижнюю полусферу, указать их области определения. Записать аналитическое выражение шара, ограниченного данной сферой и проверить, принадлежат ли ему точки .

Решение: уравнение задаёт сферу с центром в начале координат радиуса 2. Здесь, как и в примерах с параболическими цилиндрами, удобно уменьшить масштаб чертежа:

Выразим «зет»: , после чего уравнение распадается на две функции:
– задаёт верхнюю полусферу;
– задаёт нижнюю полусферу.

Область определения функции – это её ортогональная проекция на плоскость . Очевидно, что областью определения наших функций является круг с центром в начале координат радиуса 2.

Неравенство определяет шар с центром в начале координат радиуса 2. Подставим координаты точек в данное неравенство:

1)

– получено неверное неравенство, следовательно, точка «дэ» лежит вне шара.

2)

– получено верное неравенство, значит, точка «эф» принадлежит шару, а конкретнее – его границе (сфере).

Следующее задание для самостоятельного решения:

Задача 175

Найти область определения функции двух переменных и построить соответствующую поверхность.

Решение и ответ в конце книги.

Кстати, наша планета, кто не знает, имеет форму эллипсоида. Чуть-чуть-чуть, но Земля – таки не шар.

🔥 Видео

Пример решения тройного интеграла в сферических координатах - bezbotvyСкачать

§28 Эксцентриситет эллипсаСкачать

Построение кривой в полярной системе координатСкачать

§19 Исследование канонического уравнения эллипсаСкачать

Площадь фигуры через двойной интеграл в полярных координатахСкачать

Скорость и ускорение точки в полярных координатахСкачать

Площадь пересечения эллипсов и двойной интеграл в полярной системе координатСкачать