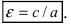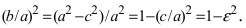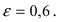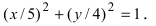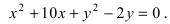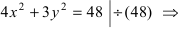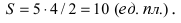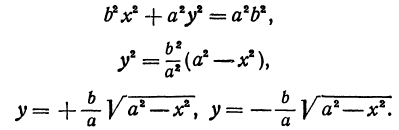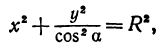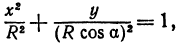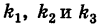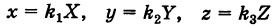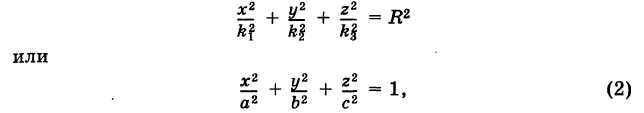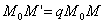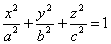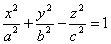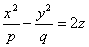Эллипс:
Определение: Эллипсом называется геометрическое место точек, сумма расстояний от которых до двух выделенных точек
Получим каноническое уравнение эллипса. Выберем декартову систему координат так, чтобы фокусы
Рис. 29. Вывод уравнения эллипса.
Расстояние между фокусами (фокусное расстояние) равно 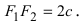
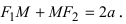
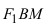
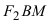
соответственно. Следовательно, согласно определению имеем
Возведем обе части равенства в квадрат, получим
Перенося квадратный корень в левую часть, а все остальное в правую часть равенства, находим 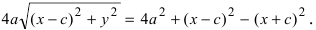
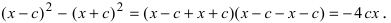
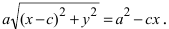
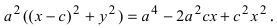
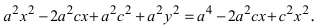
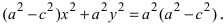
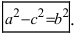
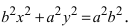
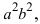
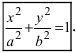
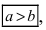
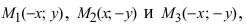
т.е. точками пересечения эллипса с осью абсцисс будут точки
т.е. точками пересечения эллипса с осью ординат будут точки
(Рис. 30).
Определение: Найденные точки называются вершинами эллипса.
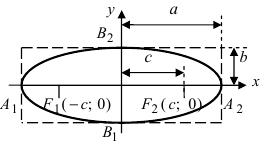
Рис. 30. Вершины, фокусы и параметры эллипса
Определение: Если 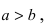
Определение: Эксцентриситетом эллипса называется отношение фокусного рас- стояния к большой полуоси эллипса
Из определения эксцентриситета эллипса следует, что он удовлетворяет двойному неравенству 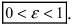
Если 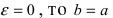
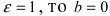
Пример:
Составить уравнение эллипса, если его большая полуось а = 5, а его эксцентриситет
Решение:
Исходя из понятия эксцентриситета, найдем абсциссу фокуса, т.е. параметр 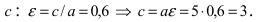
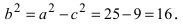
Пример:
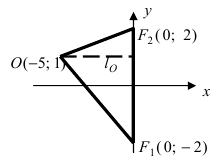
Найти площадь треугольника, две вершины которого находятся в фокусах эллипса 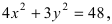
Решение:
Для определения координат фокусов эллипса и центра окружности преобразуем их уравнения к каноническому виду. Эллипс:
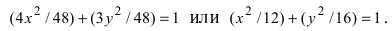
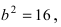
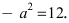
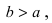
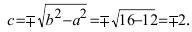
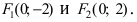
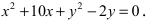
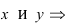
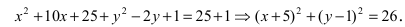
Построим в декартовой системе координат треугольник 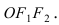
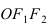
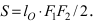
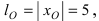
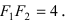
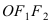
Видео:ЭллипсСкачать

Эллипс в высшей математике
где 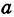
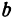
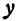
Отсюда видно, что уравнение (2) определяет две функции. Пока независимое переменное 
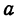

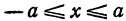
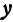
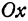
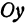
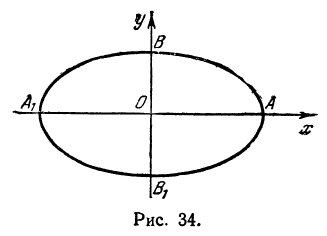
При 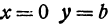
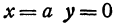
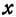

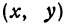
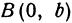
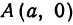
Полученная линия называется эллипсом. Число 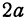
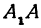
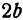
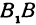
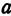
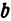
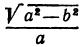
Пример:
Найти проекцию окружности на плоскость, не совпадающую с плоскостью окружности.
Решение:
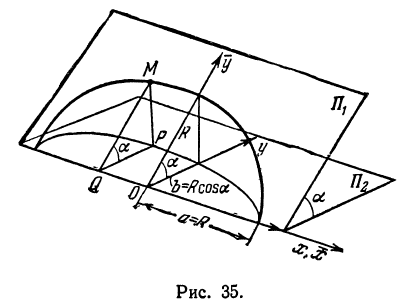
Возьмем две плоскости, пересекающиеся под углом 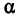
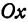
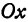
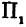
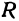
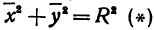
Пусть точка 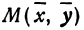
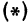
Обозначим проекцию точки 
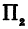
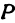
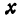
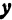


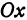
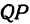
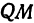
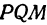
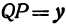
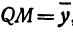
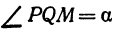
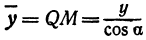


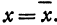
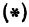
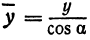
а это есть уравнение эллипса с полуосями 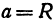
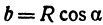
Таким образом, эллипс является проекцией окружности на плоскость, расположенную под углом к плоскости окружности.
Замечание. Окружность можно рассматривать как эллипс с равными полуосями.
Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Уравнение эллипсоида
Определение: Трехосным эллипсоидом называется поверхность, полученная в результате равномерной деформации (растяжения или сжатия) сферы по трем взаимно перпендикулярным направлениям.
Рассмотрим сферу радиуса R с центром в начале координат:
где Х, У, Z — текущие координаты точки сферы.
Пусть данная сфера подвергнута равномерной деформации в направлении координатных осей 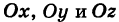
В результате сфера превратится в эллипсоид, а точка сферы М (X, У, Z) с текущими координатами Х, У, Z перейдет в точку эллипсоидам 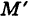
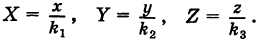
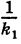
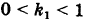
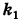
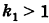
Подставляя эти формулы в уравнение (1), будем иметь
где 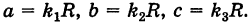
Величины 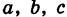
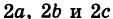
Если две полуоси эллипсоида равны между собой, то эллипсоид называется эллипсоидом вращения, так как может быть получен в результате вращения эллипса вокруг одной из его осей. Например, в геодезии считают поверхность земного шара эллипсоидом вращения с полуосями
а = b = 6377 км и с = 6356 км.
Если а = b = с, то эллипсоид превращается в сферу.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Гипербола
- Парабола
- Многогранник
- Решение задач на вычисление площадей
- Шар в геометрии
- Правильные многогранники в геометрии
- Многогранники
- Окружность
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:§28 Эксцентриситет эллипсаСкачать

Эллипсоиды
Видео:§18 Каноническое уравнение эллипсаСкачать

Определение эллипсоида
Эллипсоидом называется поверхность, определяемая в некоторой прямоугольной системе координат каноническим уравнением
где — положительные параметры, удовлетворяющие неравенствам .
Если точка принадлежит эллипсоиду (4.46), то координаты точек при любом выборе знаков также удовлетворяют уравнению (4.46). Поэтому эллипсоид (4.46) симметричен относительно координатных плоскостей, координатных осей и начала координат. Начало координат называют центром эллипсоида (4.46). Шесть точек пересечения эллипсоида с координатными осями называются его вершинами, а три отрезка координатных осей, соединяющих вершины, — осями эллипсоида. Оси эллипсоида, принадлежащие координатным осям , имеют длины соответственно. Если b>c» png;base64,iVBORw0KGgoAAAANSUhEUgAAAFEAAAAQBAMAAACcpY7MAAAAKlBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAHrpZrAAAADXRSTlMAEacB0WkhgcA75ZFRKK9ZmAAAARhJREFUKM9jYKAEJHUQq1L0igGRKhlv45dXg7N47oAppgRcruuE2cl9EUyxaUxGs2vHtgCI0h6oUhPXpgkQpYdhiiKaBBgYZgWfvQw11RWiVPaq6UKIqSrBEBkRNakNDIyLGLicoTrFIUrPBnBehdpXAlbK6GJQW8DAfodBdgPMEvHlIHKvgOV1mNOqCkAOv8MgycBgtZjh7AF4SLqDSBcG9qswlSEglVZg58k2A82A2w5iMV9i4LgGsz0QRNk2gMkCBi8msFcZ0l2ZQe5kvs6QqwDxUUmAMVgNkJvAwKLAekkExevM2gwqAiheN3JgEApg4FytuksHNeRn7VJEDXnGjiJNkIABGyjaGDURkTERTApNQMQOUAQACxo8dxA2UAQAAAAASUVORK5CYII=» />, то число называется большой полуосью, число — средней полуосью, число — малой полуосью эллипсоида. Если полуоси не удовлетворяют условиям , то уравнение (4.46) не является каноническим. Однако при помощи переименования неизвестных можно всегда добиться выполнения неравенств .
Видео:165. Найти фокусы и эксцентриситет эллипса.Скачать

Плоские сечения эллипсоида
Подставляя в уравнение (4.46), получаем уравнение линии пересечения эллипсоида с координатной плоскостью . Это уравнение в плоскости определяет эллипс Линии пересечения эллипсоида с другими координатными плоскостями также являются эллипсами. Они называются главными сечениями (главными эллипсами) эллипсоида.
Рассмотрим теперь сечение эллипсоида плоскостью, параллельной какой-нибудь координатной плоскости, например . Подставляя , где — произвольная постоянная (параметр), в уравнение (4.46), получаем
При c» png;base64,iVBORw0KGgoAAAANSUhEUgAAADoAAAAVBAMAAADlb+D4AAAAKlBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAHrpZrAAAADnRSTlMAg0KoBP0QXdEhwHEx4v6hyb4AAADaSURBVCjPY2DAD/ZAae4D2GSFGBiqlgNpRgUcsofD8ckyh+GT5W2Ay1piyk4VgMtOXoQhW1q9WAFm8uTlMAn2VWZgWdMm5gtweye3Q2i25mkXwbJXJzDGIFyVCJHOaGAMBMlyBjIwByC5OfEiiBQtYFMAybKHM7AaIMmmN4LIUKirgN49ugHJ5O4EEBUFleVtYBHNMYDJToS6KpiBgRMkmyrAsIL5AMxHUEkGCwY2c5CsqgLDXnOM0MhaaAx2FQ/QjASILJsRIpiSEiBhBQY4Y4Fs2U2wlINFFgCrpSqpbSiUhgAAAABJRU5ErkJggg==» style=»vertical-align: middle;» /> уравнение не имеет действительных решений (правая часть уравнения отрицательная, а левая неотрицательная), т.е. плоскость не пересекает эллипсоид. При уравнение (4.47) имеет нулевое решение . Следовательно, плоскости касаются эллипсоида в его вершинах . При , разделив обе части уравнения (4.47) на 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAGMAAAAwBAMAAAD3D9n/AAAAKlBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAHrpZrAAAADnRSTlMAmv2BWBABQTDA2LEhcNbL+n8AAAGvSURBVEjHY2CgJughWUeg9VRStQgyrCZVixCDFAmqWcvB1G4StDhpgUgODVJsUQSRUQ0kaGFRAenbwUKCFkYdIMHtXkiClqxlxwMYhJQUSdASNFtag6G9vIaUEFvKpkhqLDawKpOmg21VAjjMSIsWRlXStACtSNrgSpIWYLQ4uS0jSQvnAganQgd8KngC0AQSHRiYp2BXGw5OdxlGBeghlobLdObFO4Hms2lOKiA69J0CGEF+TDAioIXlKpy5moEdHGGEtKR5mUJZHMrQrERIC1ualwzUPmWgP4jRwsDGVgnRwwzSkkCMFiCo3A7TooSwxdkYBEDBHigIB8JwPYUzoFq0EojVcnAGzC9EO2w6SGWGMgOPNlHeZ4B5n00bGi9CDoS0wAKZwSiAcSlQp5KS0gRs6i7CI93LBp4tlgg1gGMqAZuOxFYpaApPMUWINuPLeUwXgqAOZksgMtUmNjBdILkaczpAqg7WJaSpb29g4G4gSUfn5I0MEhyk+IVDmU0pcbNlAQlaghaw7T05cyYp3r9EevBOaiBdSwLJWoQSGKJJ1BIl2ruCRC2p1iJ4ZAESoVYyhvDZkwAAAABJRU5ErkJggg==» style=»vertical-align: middle;» />, получаем уравнение эллипса полуосями . Следовательно, сечение эллипсоида плоскостью при представляет собой эллипс.
Плоские сечения дают возможность составить полное представление о виде эллипсоида (рис.4.40,а).
Видео:3 Полуоси эллипсаСкачать

Эллипсоиды вращения
Эллипсоид, у которого две полуоси равны, называется эллипсоидом вращения (или сфероидом ). Такой эллипсоид является поверхностью вращения. Например, если , то линии (4.47) при являются окружностями. Следовательно, сечения эллипсоида плоскостями представляют собой окружности с центрами на оси аппликат. Такую поверхность можно получить, вращая вокруг оси эллипс заданный в плоскости (рис.4.41,а).
Если , то все сечения эллипсоида (4.46) плоскостями при эллипс (рис.4.41,б).
Если все полуоси эллипсоида равны , то он представляет собой сферу радиуса , которую можно получить, например, вращая окружность такого же радиуса вокруг любого диаметра.
Эллипсоид, у которого полуоси попарно различны b>c)» png;base64,iVBORw0KGgoAAAANSUhEUgAAAGAAAAAWBAMAAADNzYTXAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAAXynYREhwNFB6DGRUQyCkmkAAAGUSURBVDjLY2AgHbBcIFYlkwOYcsYm51yCTRQsyLYUm9T2t9hEoxKABLsCNimep9hEmQ2AxL4AhG8c4EyJRjDlIoCige0ZkDiBJOahCmPFHYAY0RSArIFxEZCoAWJO49sJYAG4jnvKRWBaBK6D29ySgcEYqOYRkGO1tQ7iE0YPM4j0ubYoiIhIcwJEROuilgADEDE+AVr8ksEPFhnTwToYuwLYF0IEJIvBOljeMr5iYNQTYGB9CQytBoZzCTBnTrcGkqxvGNgfMsB0bACSeY0M2xgY/CAa/BQYuuAem1wNJHjfMsgtgApwmoM06IFd6Adx0rkJrI9h6qdbghPBM4Z5BlD1xRNAlB2YBDoJ5Gm9AN4nyRAHXYd4WughzJGyEC+AlLIxMGpBgvVeQsRLFUhEQAOJ+yn3E0hEwAJp3gVGjQAGcyBLQ4CBp8dycQFqxJ2wuIAacSxrjitAIi4PKBTKIAl2OVw9A+tGMKWEiGhpoAjbayBDWIH4rMMDcgfnUuI1gJM39gyEFTCaQDIe0VkUKfkTDwAVFViuYeRgnwAAAABJRU5ErkJggg==» style=»vertical-align: middle;» />, называется трехосным (или общим).
1. Плоскости определяют в пространстве основной прямоугольный параллелепипед , внутри которого находится эллипсоид (см. рис.4.40,б). Грани параллелепипеда касаются эллипсоида в его вершинах.
2. Эллипсоид можно определить, как геометрическое место точек, получаемое в результате трех сжатий (растяжений) сферы единичного радиуса к трем взаимно перпендикулярным плоскостям.
3. Начало канонической системы координат является центром симметрии эллипсоида, координатные оси — осями симметрии эллипсоида, координатные плоскости — плоскостями симметрии эллипсоида.
В самом деле, если точка принадлежит эллипсоиду, то точки с координатами при любом выборе знаков также принадлежат эллипсоиду, поскольку их координаты удовлетворяют уравнению (4.46).
Видео:Аналитическая геометрия: Эллипс, Парабола, Гипербола. Высшая математикаСкачать

Уравнение эллипсоида и его полуоси
Видео:Лекция 31.1. Кривые второго порядка. ЭллипсСкачать

Глава 46. Поверхности второго порядка
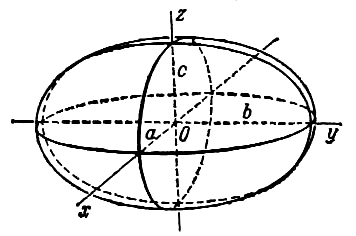
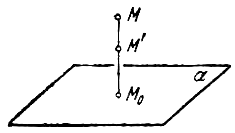
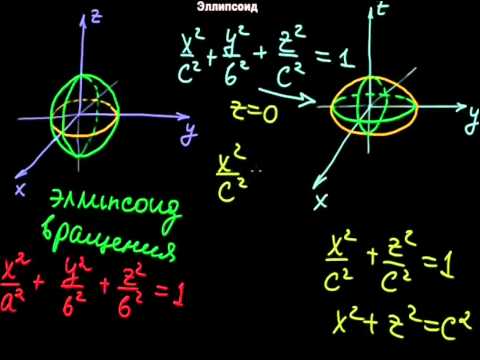
Эллипсоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением
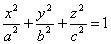
Уравнение (1) называется каноническим уравнением эллипсоида. Величины a, b, c суть полуоси эллипсоида (рис. 1). Если все они различны, эллипсоид называется трехосным; в случае, когда какие-нибудь две из них одинаковы, эллипсоид называется вытянутым, при a=b>c — сжатым. В случае, когда a=b=c , эллипсоид представляет собой сферу.
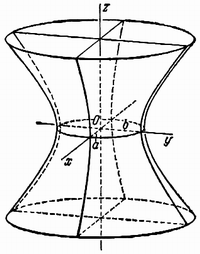
Гиперболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями
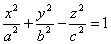
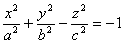
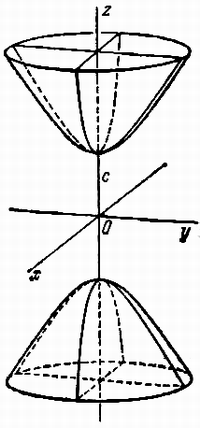
Гиперболоид, определяемый уравнением (2), называется однополостным (рис. 2); гиперболоид, определяемый уравнением (3), — двуполостным (рис. 3); уравнения (2) и (3) называются каноническими уравнениями соответствующих гиперболоидов. Величины a, b, c называются полуосями гиперболоида. В случае однополостного гиперболоида, заданного уравнением (2), только первые из них (а и b ) показаны на рис. 2. В случае двуполостного гиперболоида, заданного уравнением (3), одна из них (именно, с) показана на рис. 3. Гиперболоиды, определяемые уравнениями (2) и (3), при a=b являются поверхностями вращения.
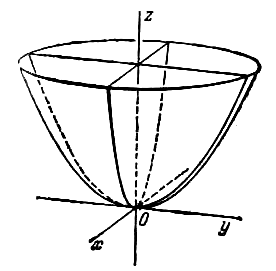
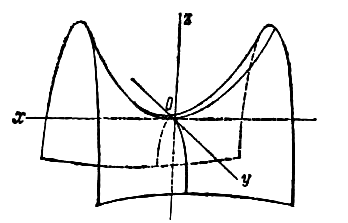
Параболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями
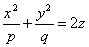
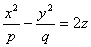
где p и q — положительные числа, называемые параметрами параболоида. Параболоид, определяемый уравнением (4), называется эллиптическим (рис. 4); параболоид, определяемый уравнением (5), — гиперболическим (рис. 5). Уравнения (4) и (5) называют каноническими уравнениями соответствующих параболоидов. В случае, когда p=q , параболоид, определяемый уравнением (4), является поверхностью вращения (вокруг Oz).
Рассмотрим теперь преобразование пространства, которое называется равномерным сжатием (или равномерным растяжением).
Выберем какую-нибудь плоскость; обозначим ее буквой 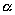
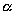
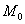
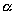
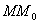
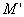
и чтобы после перемещения точка осталась с той же стороны от плоскости 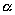
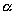
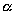
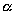
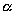
Пусть дана некоторая поверхность F ; при равномерном сжатии пространства точки, которые ее составляют, переместятся и в новых положениях сотавят поверхность F ’. Будем говорить, что поверхность F ’ получено из F в результате равномерного сжатия пространства. Оказывается, что многие поверхности второго порядка (все, кроме гиперболического параболоида) можно получить в результате равномерного сжатия из поверхностей вращения).
ПРИМЕР. Доказать, что произвольный трехосный эллипсоид
может быть получен из сферы
в результате двух последовательных равномерных сжатий пространства к координатным плоскостям: к плоскости Oxy с коэффициентом сжатия 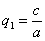
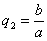
ДОКАЗАТЕЛЬСТВО. Пусть производится равномерное сжатие пространства к плоскости Oxy с коэффициентом 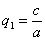
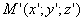
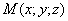
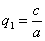
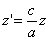
Таким образом, мы получаем искомые выражения:
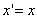
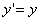
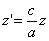
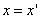
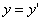
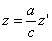
Предположим, что M(x; y; z ) — произвольная точка сферы
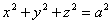
Заменим здесь x, y, z их выражениями (7); получим
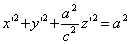
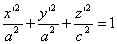
Следовательно, точка M’(x’; y’; z ’) лежит на эллипсоиде вращения. Аналогично, мы должны осуществить сжатие пространства к плоскости Oxz по формулам
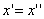
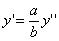
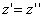
тогда получим трехосный эллипсоид и именно тот, уравнение которого дано в условии задачи.
Отметим еще, что однополостный гиперболоид и гиперболический параболоид суть линейчатые поверхности, то есть они состоят из прямых; эти прямые называются прямолинейными образующими указанных поверхностей.
имеет две системы прямолинейных образующих, которые определяются уравнениями:
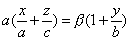
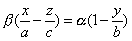
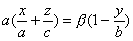
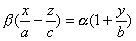
где 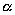
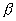
также имеет две системы прямолинейных образующих, которые определяются уравнениями
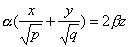
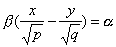
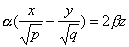
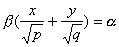
Конической поверхностью, или конусом, называется поверхность, которая описывается движущейся прямой (образующей) при условии, что эта прямая проходит через постоянную точку S и пересекает некоторую определенную линию L . Точка S называется вершиной конуса; линия L — направляющей.
Цилиндрической поверхностью, или цилиндром, называется поверхность, которая описывается движущейся прямой (образующей) при услвоии, что эта прямая имеет постоянное направление и пересекает некоторую определенную линию L (направляющую).
🎦 Видео
Эллипс. Определение. Уравнение. График. Фокусы. Главные оси. Эксцентриситет - Новиков АлександрСкачать

§31.1 Приведение уравнения кривой к каноническому видуСкачать

Как найти полуоси эллипса, вписанного в равнобедренную трапецию?Скачать

§17 Определение эллипсаСкачать

Видеоурок "Эллипс"Скачать

§65 ЭллипсоидСкачать
11 класс, 52 урок, ЭллипсСкачать

Кривые второго порядка. Эллипс. Приведение к каноническому виду и чертежСкачать

Видеоурок "Гипербола"Скачать

Определить тип кривой (эллипс)Скачать

Уравнение эллипса. Нахождение вершин и фокусовСкачать

Эллипс (часть 1). Каноническое уравнение. Высшая математика.Скачать

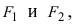
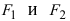
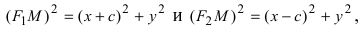
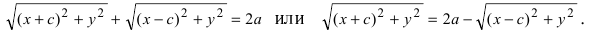
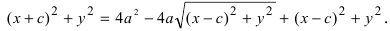
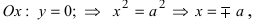 т.е. точками пересечения эллипса с осью абсцисс будут точки
т.е. точками пересечения эллипса с осью абсцисс будут точки 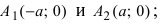
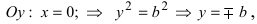 т.е. точками пересечения эллипса с осью ординат будут точки
т.е. точками пересечения эллипса с осью ординат будут точки 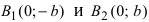 (Рис. 30).
(Рис. 30).