Уравнение эллипса в полярных координатах с центром в начале координат (3 видео)

ЛИНИИ И ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА

Содержание

Алгебраические линии и порядок
Эллипс
Математический портал
Nav view search
Navigation
Search
Уравнение эллипса, гиперболы, параболы в полярной системе координат.
05.3. Уравнения эллипса, гиперболы и параболы
Уравнения эллипса, гиперболы и параболы В полярной системе координат
🔥 Видео

Видео:Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

Алгебраические линии и порядок

Определение 10.1. Поверхность называется алгебраической, если в некоторой системе координат она удовлетворяет уравнению fix, у, z) = 0, где fix, у, z) — многочлен.

Определение 10.2. Алгебраическая поверхность называется поверхностью порядка п, если она определяется уравнением степени п.

Теорема 10.1. Если поверхность определяется относительно некоторой системы координат уравнением степени п, то относительно любой другой системы она также определяется уравнением степени п.

Видео:§30 Уравнения кривых второго порядка в полярных координатахСкачать

Эллипс

Определение 10.3. Эллипсом называется линия, которая в некоторой прямоугольной системе координат определяется уравнением

Рассмотрим точки с координатами (с, 0) и (-с, 0), где

(рис. 10.1). Эти точки называются фокусами эллипса.

Вычислим сумму расстояний от фокусов до произвольной точки эллипса М(х, у).

Имеем:

Таким образом, получаем:

Видео:Полярные координаты. Полярное уравнение эллипса.Скачать

Математический портал

Видео:Построение кривой в полярной системе координатСкачать

Nav view search

Search

Вы здесь:
Home
Аналитическая геометрия
Высшая математика.
Аналитическая геометрия.
Уравнение эллипса, гиперболы, параболы в полярной системе координат.

Видео:Полярная система координатСкачать

Уравнение эллипса, гиперболы, параболы в полярной системе координат.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Пример.

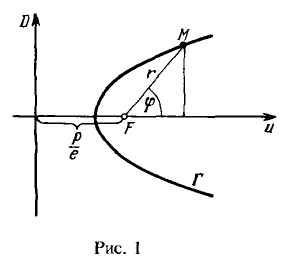
Пусть $Gamma -$ эллипс, ветвь гиперболы или парабола, $F -$ фокус этой кривой, $D -$ соответствующая директриса. Вывести уравнение кривой $Gamma$ в полярной системе координат, полюс которой совпадает с фокусом а полярная ось сонаправлена с осью кривой (см рисунок 1).

Решение.

Общее свойство эллипса, гиперболы и параболы состоит в следующем $$MinGammaLeftrightarrowfrac=const=e,qquadqquad (1)$$ где $e -$ эксцентриситет кривой ( $e 1$ для гиперболы и $e=1$ для параболы)

Обозначим расстояние от фокусы до директрисы через $frac

$( $p-$ параметр кривой, называемый полуфокальным параметром). Тогда из рисунка 1 следует, что $rho(M, F)=r$ и $rho(M, D)=frac

+rcosvarphi.$ Подставляя эти выражения в (1), получаем $$frac<frac

+rcosvarphi>=e,$$ откуда $$r=frac

.qquadqquad (2)$$ Уравнение (2) и есть искомое уравнение в полярной системе координат, общее для эллипса, гиперболы и параболы.

Примеры.

2.321(а).

Для эллипса $frac+frac=1$ написать полярное уравнение, считая, что полярная ось сонаправлена с осью абсцисс, а полюс находится в левом фокусе.

Решение.

Найдем эксцентриситет параболы и параметр $p:$

Далее, подставляя найденные параметры в полярное уравнение (2), найденное в предыдущей задаче, найдем уравнение данного эллипса:

2.324(а).

Написать каноническое уравнение кривой второго порядка $r=frac.$

Решение.

Приведем заданное уравнение, к уравнению вида $r=frac

Отсюда имеем: $e=frac,$ $p=frac.$ Поскольку $e

Далее, подставляя выражения эксцентриситета и параметра по определению, надем полуоси эллипса:

Таким образом, запишем каноническое уравнение эллипса:

Вывести полярное уравнение гиперболы $frac-frac=1,$ при условии, что полярная ось сонаправлена с осью $Ox,$ а полюс находится в центре гиперболы.

Решение.

Так как полюс находится в центре гиперболы, то $OM=r,$ тогда $rho(M, D)=rcosvarphi-frac,$ $rho(M, F)=sqrt .$

Таким образом, из уравнения (1) находим:

Домашнее задание.

2.321(б) Для эллипса $frac+frac=1$ написать полярное уравнение, считая, что полярная ось сонаправлена с осью абсцисс, а полюс находится в правом фокусе.

2.322. Для правой ветви гиперболы $frac-frac=1$ написать полярное уравнение, считая, что полярная ось сонаправлена с осью абсцисс, а полюс находится

а) в левом фокусе, б) в правом фокусе.

2.323. Для параболы $y^2=6x$ написать полярное уравнение, считая, что полярная ось сонаправлена с осью абсцисс, а полюс находится в фокусе параболы.

2.324 (б, в) Написать канонические уравнения следующих кривых второго порядка:

Ответ: а) $frac-frac=1,$ б) $y^2=6x.$

2.327. Вывести полярное уравнение параболы $y^2=2px$ при условии, что полярная ось сонаправленна с осью $Ox,$ а полюс находится в вершине параболы.

Видео:Оператор Лапласа в полярных координатахСкачать

05.3. Уравнения эллипса, гиперболы и параболы

Уравнения эллипса, гиперболы и параболы
В полярной системе координат

Нам уже известно, что в полярной системе координат окружность с центром в начале отсчета задается уравнением:

Где r – радиус окружности, а – полярный радиус.

Интуитивно легко угадывается расположение начала отсчета, при котором уравнение окружности имеет более простой вид. Эта проблема усложняется при выводе уравнений эллипса, гиперболы и параболы.

Рассмотрим сначала отличный от окружности эллипс и параболу. Проведем рассуждения для параболы. Пусть начало полярной системы координат находится в полюсе F, а полярная ось перпендикулярна директрисе и ориентирована, как указано на рис. 5.18. Возьмем произвольную точку на данной кривой.

Рис. 5.18. Расположение полярной системы координат при выводе уравнений эллипса и параболы.

Как уже известно, для точек эллипса и параболы и только для них

Где – расстояние от этой точки до фокуса F, а – расстояние до директрисы, е – эксцентриситет.

Где р – расстояние от фокуса F до директрисы, то

Как параметр р выражается через полуоси эллиптической кривой?

Каким будет уравнение этих кривых, если начало полярной системы координат перенести в точку С, а полярную ось — параллельно самой себе, не меняя ориентации ?

(5.11)

Это есть уравнение эллипса или параболы в полярной системе координат.

Перейдем к выводу уравнения гиперболы в полярной системе координат.

Пусть F – один из фокусов гиперболы (рис.5.19), а р=AC, – эксцентриситет гиперболы. Располагаем начало отсчета в фокусе F и ориентируем полярную ось, как указано на рис. 5.19.

Рис. 5.19. Расположение полярной системы координат при выводе уравнения гиперболы.

Для правой ветви гиперболы, повторяя предыдущие рассуждения, сразу получим уравнение вида (5.11).

Найдем уравнение левой ветви. Для точек гиперболы будет справедливо соотношение . Пусть – произвольная точка, лежащая на левой ветви (рис. 5.19). Имеем: