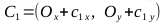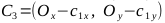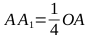IP76 > Координаты точки эллипса по углу
Для нахождения координат точки эллипса по углу существует простое и элегантное решение. Понимаю, что для маститого математика это решение является очевидным. Однако, для меня в то далекое время, когда инет был диким, связь модемной, а я сильно молодым, это таковым не являлось.
Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Калькулятор точки на эллипсе
Давайте посмотрим, как это выглядит на практике. Потом теория. Оранжевый маркер отвечает за угол, на основании которого считаем координаты. Красный — параметрический угол, о котором ниже.
Get a better browser, bro…
Видео:10 класс, 43 урок, Уравнение касательной к графику функцииСкачать

Параметрическое уравнение эллипса
Обратимся, как обычно, к Википедии. Находим там следующее:
Каноническое уравнение эллипса может быть параметризовано:
Очевидно, что t — это угол, и это не «наш» угол. Это какой-то другой угол, который функционально связан с «нашим». «Нашим» называю угол, от которого требуется посчитать координаты.
Таким образом, задача нахождения координат точки эллипса по углу сводится к задаче нахождения угла t, зависящим от требуемого. Нахождением этой зависимости и займемся.
Видео:Аналитическая геометрия: Эллипс, Парабола, Гипербола. Высшая математикаСкачать

Подготовка
У нас есть эллипс, описанный двумя полуосями a и b. Представим две окружности, имеющих общий центр. Меньшая окружность (зеленая) имеет радиус b. Большая окружность (синяя) имеет радиус a.
Проведем прямую из общего центра [X0;Y0] в произвольную точку плоскости [X;Y]. В результате пересечения с этими окружностями получаются две точки [X1;Y1] и [X2;Y2].
α – угол между прямой и осью X.
| Малая окружность | X1 = b × cos α | Y1 = b × sin α |
| Большая окружность | X2 = a × cos α | Y2 = a × sin α |
Таблица 1. Координаты точек пересечения прямой с окружностями
Видео:§18 Каноническое уравнение эллипсаСкачать

Нахождение зависимости
Используя уравнение (1) посчитаем координаты точки на эллипсе [X’;Y’] для угла α. Проведем прямую из центра [X0;Y0] в точку [X’;Y’]. Угол β – угол между этой прямой и осью X.
Задача сводится к тому, чтобы найти такой α, при котором β был бы равен интересующему нас углу. Таким образом, угол α будет являться параметром в уравнении (1) для требуемого угла β.
Найдем зависимость между получившимся углом β и углом α. На рисунке видно, что прилегающий к углу катет (синий) равен ранее рассчитанному X2, а противолежащий (зеленый) равен Y1:
X’ = X2 = a × cos α
Y’ = Y1 = b × sin α
Опыт показывает, что тут зачастую возникает легкий ступор. Возможно, рисунок вводит в некое заблуждение. Видим треугольник, и если с синим катетом вопросов нет, то с зеленым — масса. Почему синус от α? Угол «вона где», тут синус вообще не от того угла и т.д.
Смотрим на пересечение прямой и малой (зеленой) окружности. Зеленый катет прилетает именно оттуда. Именно так координату Y’ и рассчитывали, согласно уравнению(1). Рисунок — это иллюстрация, не метод решения.
Тангенс угла β в этом случае равен:
(3) Тангенс угла β
Используя формулу тангенса произведем дальнейшие преобразования:
(4) Зависимость тангенса α от тангенса β
Таким образом, видим прямую зависимость угла α, который нужен нам в качестве параметра в уравнении(1), от угла β, координаты точки от которого хотим получить.
Видео:§28 Эксцентриситет эллипсаСкачать

Нахождение координат
Угол α находим через арктангенс. В Delphi (и не только) для этих целей используется функция ArcTan2 из модуля math. Она корректно возвращает знак ± угла в зависимости от квадранта, а также предусмотрительно нечувствительна к возможным коллизиям, типа деления на 0.
Находим синус и косинус от требуемого угла β и подставляем в параметры функции ArcTan2, согласно последней формуле (4):
Видео:11 класс, 52 урок, ЭллипсСкачать

Рисование эллипса под произвольным углом в canvas на JavaScript
В процессе разработки одного приложения столкнулся с необходимостью рисования эллипсов под произвольным углом в canvas на JavaScript. Пользоваться какими-либо фреймворками в столь простом проекте не хотелось, так что я отправился на поиски статьи-мануала на эту тему. Поиски не увенчались успехом, так что пришлось разбираться с задачей самостоятельно, и я решил поделиться с вами полученным опытом.
Формализуем задачу. Нам требуется функция drawEllipse(coords, sizes, vector), где:
- coords — координаты центра эллипса — массив [x, y]
- sizes — длины большой и малой полуосей эллипса — массив [a, b]
- vector — вектор [x, y] наклона эллипса
В статье приведено три способа решения данной задачи.
В качестве первого метода были выбраны кривые Безье. Для построения такой кривой требуются четыре точки: начальная, конечная и две контрольные.
Искомый эллипс будет состоять из двух таких кривых, причем нетрудно догадаться, что вышеупомянутые точки у каждой из них будут вершинами прямоугольника. Давайте исследуем наш эллипс.
- Имеем некоторый вектор
Найдем единичный вектор
Найдем единичный вектор
Для этого вспомним свойство скалярного произведения векторов обращаться в ноль в случае, если они перпендикулярны:
Таким образом: - Найдем векторы
, точки A1, A2, B1, B2
- Найдем векторы
, точки C1, C2, C3, C4
- Вспомним, что для рисования эллипса нам нужны две кривые Безье:
- 1-я имеет начальную точку B1, конечную B2, проходит через точку A1
- 2-я имеет начальную точку B2, конечную B1, проходит через точку A2
Вспомним также, что для построения кривых Безье нам требуются контрольные точки. Недолго думая, я сначала подставил в качестве таковых вершины прямоугольника, в который вписан эллипс. Это решение оказалось ошибкой, ведь если мы рассмотрим построение кривой Безье, то обнаружим, что она не касается отрезка, соединяющего две контрольные точки.
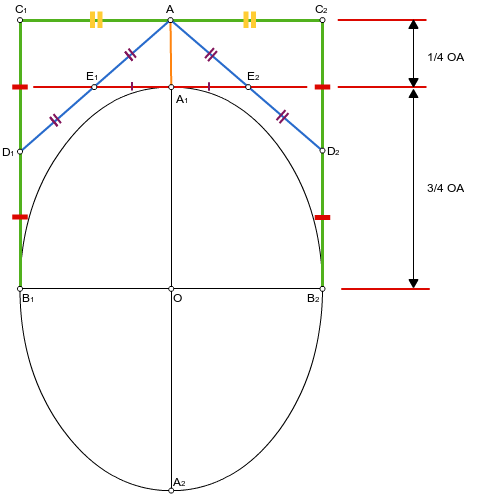
Изобразим момент построения кривой Безье в точке, в которой она (кривая) будет наиболее близка к отрезку между контрольными точками. В нашем случае это будет выглядеть так:
Из рисунка очевидно, что расстояние от этой точки (A1) до отрезка между контрольными точками (C1, C2) будет составлять четверть от расстояния между центром искомого эллипса (O) и тем же отрезком (C1, C2), то есть:



Таким образом, для получения эллипса с нужными параметрами нам необходимо умножить вектор
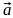 на параметр
на параметр 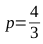 , после чего вернуться к вычислениям, описанным в пунктах 1-4. В результате получаем наборы точек (B1, C1, C2, B2 и B2, C3, C4, B1) для построения двух кривых Безье, вместе представляющих искомую фигуру.
, после чего вернуться к вычислениям, описанным в пунктах 1-4. В результате получаем наборы точек (B1, C1, C2, B2 и B2, C3, C4, B1) для построения двух кривых Безье, вместе представляющих искомую фигуру.Собственно демо и код:
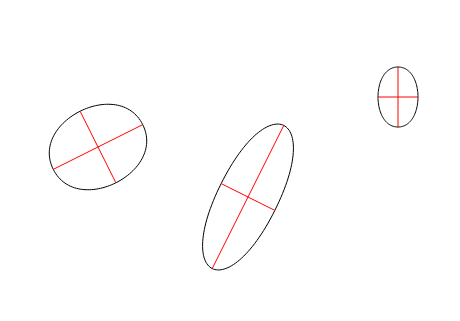
Upd. Ознакомившись с комментариями, написал функцию рисования эллипса через параметрическое уравнение, и оказалось, что фигура, которая получается с помощью кривых Безье не вполне точно совпадает с эллипсом. На наложении фигур видно, что нарисованный кривыми Безье объект (красный) местами шире, чем правильный эллипс (синий). Вот демо наложения фигур.
Upd. В комментариях подсказали более нативный и простой способ отрисовки наклонного эллипса (спасибо subzey). Оставлю здесь, чтобы не затерялся. Вот демо.
Видео:Поворот и параллельный перенос координатных осей. ЭллипсСкачать
Эллипс
Видео:Математика без Ху!ни. Уравнение касательной.Скачать

Определение эллипса.
Напомним, что мы назвали эллипсом линию, которая в некоторой декартовой прямоугольной системе координат определяется каноническим уравнением
$$
frac<x^><a^>+frac<y^><b^>=1label
$$
при условии (a geq b > 0).
Из уравнения eqref следует, что для всех точек эллипса (|x| leq a) и (|y| leq b). Значит, эллипс лежит в прямоугольнике со сторонами (2a) и (2b).
Точки пересечения эллипса с осями канонической системы координат, имеющие координаты ((a, 0)), ((-a, 0)), ((0, b)) и ((0, -b)), называются вершинами эллипса. Числа (a) и (b) называются соответственно большой и малой полуосями эллипса.
Рис. 8.1. Эллипс
В каноническое уравнение входят только квадраты координат. Поэтому, если координаты ((x, y)) какой-либо точки /(M) ему удовлетворяют, то ему удовлетворяют и координаты ((-x, y)), ((x, -y)) и ((-x, -y)) точек (M_), (M_) и (M_) (рис. 8.1). Следовательно, справедливо следующее утверждение.
Оси канонической системы координат являются осями симметрии эллипса, а начало канонической системы — его центром симметрии.
Внешний вид эллипса проще всего описать сравнением с окружностью радиуса (a) с центром в центре эллипса: (x^+y^=a^). При каждом (x) таком, что (|x| Рис. 8.2. Сжатие окружности к эллипсу. Ординаты всех точек уменьшаются в отношении (b/a).
Видео:Найти все касательные к эллипсу проходящие через начало координатСкачать

Фокусы, эксценриситет и директрисы эллипса.
У эллипса есть две замечательные точки, которые называются его фокусами.
Фокусами называются точки (F_) и (F_) с координатами ((c, 0)) и ((-c, 0)) в канонической системе координат (рис. 8.3).
Рис. 8.3. Фокусы эллипса.
Для окружности (c=0), и оба фокуса совпадают с центром. Ниже мы будем предполагать, что эллипс не является окружностью.
Отметим, что (varepsilon Утверждение 2.
Расстояние от произвольной точки (M(x, y)), лежащей на эллипсе, до каждого из фокусов (рис. 8.3) является линейной функцией от ее абсциссы (x):
$$
r_=|F_M|=a-varepsilon x, r_=|F_M|=a+varepsilon x.label
$$
Очевидно, что (r_^=(x-c)^+y^). Подставим сюда выражение для (y^), найденное из уравнения эллипса. Мы получим
$$
r_^=x^-2cx+c^+b^-frac<b^x^><a^>.nonumber
$$
Учитывая равенство eqref, это можно преобразовать к виду
$$
r_^=a^-2cx+frac<c^x^><a^>=(a-varepsilon x)^.nonumber
$$
Так как (x leq a) и (varepsilon Утверждение 3.
Для того чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы сумма ее расстояний до фокусов равнялась большой оси эллипса (2a).
Необходимость. Если мы сложим равенства eqref почленно, то увидим, что
$$
r_+r_=2a.label
$$
Достаточность. Пусть для точки (M(x, y)) выполнено условие eqref, то есть
$$
sqrt<(x-c)^+y^>=2a-sqrt<(x+c)^+y^>.nonumber
$$
Возведем обе части равенства в квадрат и приведем подобные члены:
$$
xc+a^=asqrt<(x+c)^+y^>.label
$$
Это равенство также возведем в квадрат и приведем подобные члены, используя соотношение eqref. Мы придем к (b^x^+a^y^=a^b^), равносильному уравнению эллипса eqref.
Рис. 8.4. Фокусы и директрисы эллипса.
Для того чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы отношение ее расстояния до фокуса к расстоянию до соответствующей директрисы равнялось эксцентриситету эллипса (varepsilon).
Видео:Овчинников А. В. - Аналитическая геометрия - Эллипс, гипербола, параболаСкачать

Уравнение касательной к эллипсу.
Выведем уравнение касательной к эллипсу, заданному каноническим уравнением. Пусть (M_(x_, y_)) — точка на эллипсе и (y_ neq 0). Через (M_) проходит график некоторой функции (y=f(x)), который целиком лежит на эллипсе. (Для (y_ > 0) это график (f_(x)=bsqrt<1-x^/a^>), для (y_ Утверждение 5.
Касательная к эллипсу в точке (M_(x_, y_)) есть биссектриса угла, смежного с углом между отрезками, соединяющими эту точку с фокусами.
Рис. 8.5.
💡 Видео
ЭллипсСкачать

Эллипс (часть 1). Каноническое уравнение. Высшая математика.Скачать

Лекция 31.1. Кривые второго порядка. ЭллипсСкачать

Кривые второго порядка. Эллипс. Приведение к каноническому виду и чертежСкачать

Эллипс (часть 8). Решение задач. Высшая математика.Скачать

Разбор задания из теста по ангему | Уравнение эллипса | Уравнение касательной к эллипсуСкачать

§20 Построение эллипсаСкачать
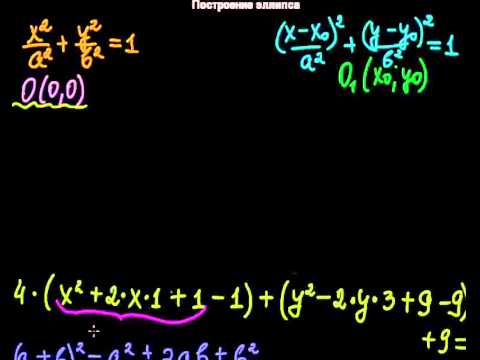
Эллипс, парабола и гипербола. Конические сечения | Ботай со мной #055 | Борис Трушин |Скачать

найти уравнение касательной к эллипсуСкачать

Аналитическая геометрия, 7 урок, Линии второго порядкаСкачать






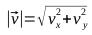
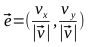


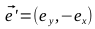
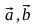 , точки A1, A2, B1, B2
, точки A1, A2, B1, B2
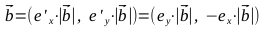

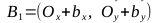


 , точки C1, C2, C3, C4
, точки C1, C2, C3, C4