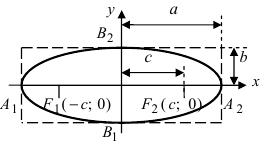
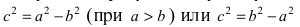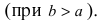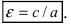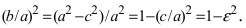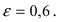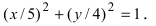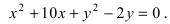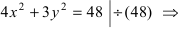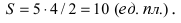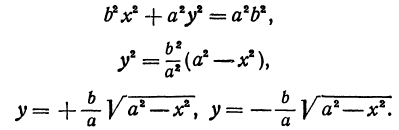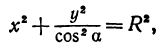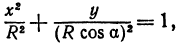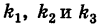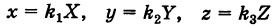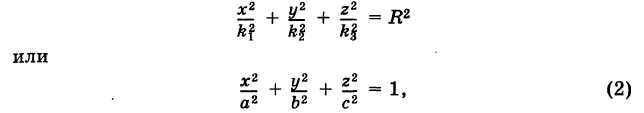Вернёмся к каноническому уравнению эллипса 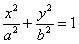
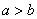
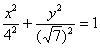
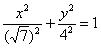
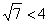
Подобное уравнение нечасто, но действительно попадается. И оно действительно определяет эллипс. Развеем мистику:
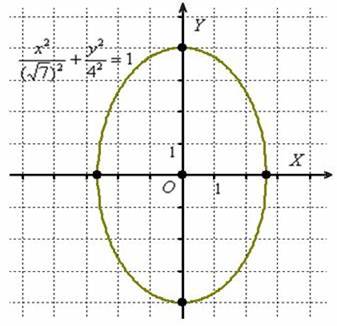
В результате построения получен наш родной эллипс, повёрнутый на 90 градусов. То есть, 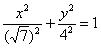
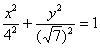
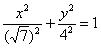
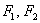
Как быть, если такое чудо-яйцо всё-таки встретилось на жизненном пути? В том случае если вам предложено построить эллипс, то, наверное, лучше построить его в нестандартном виде. С вершинами и дополнительными точками, думаю, трудностей не возникнет. Но если вам предложено найти фокусы, эксцентриситет и т.д., то настоятельно рекомендую начать (или продолжить после чертежа) решение так:
«Повернём эллипс на 90 градусов и перепишем его уравнение 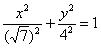
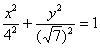
! Примечание: в теории принято поворачивать не саму фигуру, а оси! И если от васТРЕБУЕТСЯ привести уравнение к каноническому виду, то решение, строго говоря, следует оформить иначе: «Перейдём к новой прямоугольной системе координат 
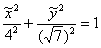
Впрочем, эрудиты могут встать на скользкую дорожку путаницы, модифицировав все расчёты с учётом поворота. Но всё равно не советую. Потому что ребячество. Ведь эллипс можно повернуть и на другой угол =) Об этом мы ещё поговорим позже.
В практических задачах гораздо чаще встречается параллельный перенос эллипса:
Уравнение 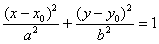
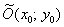
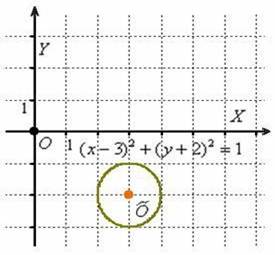
Изобразим на чертеже эллипс 
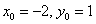
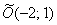
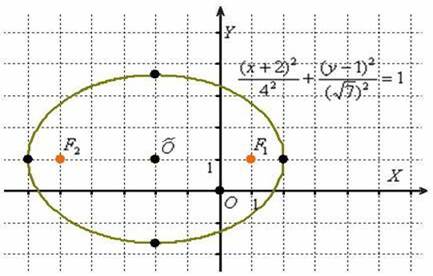
Значения 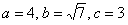
Здесь всё обходится значительно проще, чем при повороте, и если по условию не нужноприводить уравнение к каноническому виду, то лично я предпочту оставить его в виде 

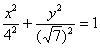
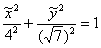
На самом деле упрощенная версия формулы нам знакома ещё со школьных времён:
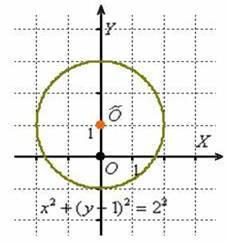
Уравнение 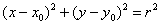
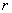
Освежая ностальгические воспоминания, изобразим на чертеже окружность, заданную уравнением 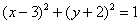
В исследовательских целях приведём наше уравнение к общему виду, выполнив возведение в квадрат и приведение подобных слагаемых:
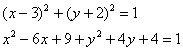
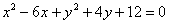
Таким образом, в практических задачах часто предварительно нужно выполнить обратное действие – выделить полные квадраты. Данный приём подробно разобран на уроках огеометрических преобразованиях графиков и интегрировании дробей. Хотя следующий простой пример не должен вызвать у вас затруднений даже без отработки данного метода:
Построить график линии, заданной уравнением
Решение и чертёж в конце урока.
На практике эллипс (как и другие линии) может быть одновременно повёрнут на любой угол относительно своего канонического положения и перенесен в любую точку, отличную от начала координат. В таком случае решается типовая задача приведения линии 2-го порядка к каноническому виду, к которой я потихоньку начал вас готовить уже сегодня.
Ну а пока самое время перейти ко второй части лекции, где жертвами станут гипербола и парабола.
Решения и ответы:
Пример 2: Решение: поскольку фокусы канонически расположенного эллипса имеют координаты 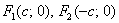
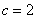
По условию известно значение 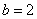
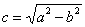
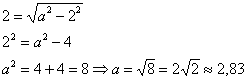
Запишем каноническое уравнение эллипса:
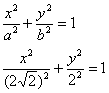
Вершины эллипса расположены в точках 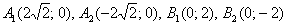
Найдём дополнительные точки:

Выполним чертёж:
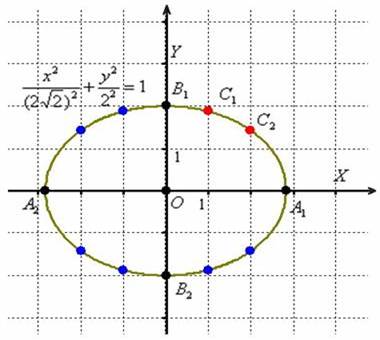
Вычислим эксцентриситет:
Пример 3: Решение: выделим полный квадрат:
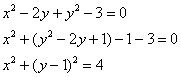
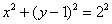
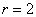
Выполним чертёж:
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)
Как можно отблагодарить автора?
Гипербола и парабола
Переходим ко второй части статьи о линиях второго порядка, посвященной двум другим распространённым кривым – гиперболе и параболе. Если вы зашли на данную страницу с поисковика либо ещё не успели сориентироваться в теме, то рекомендую сначала изучить первый раздел урока, на котором мы рассмотрели не только основные теоретические моменты, но и познакомились с эллипсом. Остальным же читателям предлагаю существенно пополнить свои школьные знания о параболе и гиперболе. Гипербола и парабола – это просто? …Не дождётесь =)
Видео:11 класс, 52 урок, ЭллипсСкачать

Координаты точки эллипса по углу
IP76 > Координаты точки эллипса по углу
Для нахождения координат точки эллипса по углу существует простое и элегантное решение. Понимаю, что для маститого математика это решение является очевидным. Однако, для меня в то далекое время, когда инет был диким, связь модемной, а я сильно молодым, это таковым не являлось.
Видео:Аналитическая геометрия: Эллипс, Парабола, Гипербола. Высшая математикаСкачать

Калькулятор точки на эллипсе
Давайте посмотрим, как это выглядит на практике. Потом теория. Оранжевый маркер отвечает за угол, на основании которого считаем координаты. Красный — параметрический угол, о котором ниже.
Get a better browser, bro…
Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Параметрическое уравнение эллипса
Обратимся, как обычно, к Википедии. Находим там следующее:
Каноническое уравнение эллипса может быть параметризовано:
Очевидно, что t — это угол, и это не «наш» угол. Это какой-то другой угол, который функционально связан с «нашим». «Нашим» называю угол, от которого требуется посчитать координаты.
Таким образом, задача нахождения координат точки эллипса по углу сводится к задаче нахождения угла t, зависящим от требуемого. Нахождением этой зависимости и займемся.
Видео:Разбор задания из теста по ангему | Уравнение эллипса | Уравнение касательной к эллипсуСкачать

Подготовка
У нас есть эллипс, описанный двумя полуосями a и b. Представим две окружности, имеющих общий центр. Меньшая окружность (зеленая) имеет радиус b. Большая окружность (синяя) имеет радиус a.
Проведем прямую из общего центра [X0;Y0] в произвольную точку плоскости [X;Y]. В результате пересечения с этими окружностями получаются две точки [X1;Y1] и [X2;Y2].
α – угол между прямой и осью X.
| Малая окружность | X1 = b × cos α | Y1 = b × sin α |
| Большая окружность | X2 = a × cos α | Y2 = a × sin α |
Таблица 1. Координаты точек пересечения прямой с окружностями
Видео:ЭллипсСкачать

Нахождение зависимости
Используя уравнение (1) посчитаем координаты точки на эллипсе [X’;Y’] для угла α. Проведем прямую из центра [X0;Y0] в точку [X’;Y’]. Угол β – угол между этой прямой и осью X.
Задача сводится к тому, чтобы найти такой α, при котором β был бы равен интересующему нас углу. Таким образом, угол α будет являться параметром в уравнении (1) для требуемого угла β.
Найдем зависимость между получившимся углом β и углом α. На рисунке видно, что прилегающий к углу катет (синий) равен ранее рассчитанному X2, а противолежащий (зеленый) равен Y1:
X’ = X2 = a × cos α
Y’ = Y1 = b × sin α
Опыт показывает, что тут зачастую возникает легкий ступор. Возможно, рисунок вводит в некое заблуждение. Видим треугольник, и если с синим катетом вопросов нет, то с зеленым — масса. Почему синус от α? Угол «вона где», тут синус вообще не от того угла и т.д.
Смотрим на пересечение прямой и малой (зеленой) окружности. Зеленый катет прилетает именно оттуда. Именно так координату Y’ и рассчитывали, согласно уравнению(1). Рисунок — это иллюстрация, не метод решения.
Тангенс угла β в этом случае равен:
(3) Тангенс угла β
Используя формулу тангенса произведем дальнейшие преобразования:
(4) Зависимость тангенса α от тангенса β
Таким образом, видим прямую зависимость угла α, который нужен нам в качестве параметра в уравнении(1), от угла β, координаты точки от которого хотим получить.
Видео:§18 Каноническое уравнение эллипсаСкачать

Нахождение координат
Угол α находим через арктангенс. В Delphi (и не только) для этих целей используется функция ArcTan2 из модуля math. Она корректно возвращает знак ± угла в зависимости от квадранта, а также предусмотрительно нечувствительна к возможным коллизиям, типа деления на 0.
Находим синус и косинус от требуемого угла β и подставляем в параметры функции ArcTan2, согласно последней формуле (4):
Видео:Видеоурок "Эллипс"Скачать

Эллипс — определение и вычисление с примерами решения
Эллипс:
Определение: Эллипсом называется геометрическое место точек, сумма расстояний от которых до двух выделенных точек
Получим каноническое уравнение эллипса. Выберем декартову систему координат так, чтобы фокусы
Рис. 29. Вывод уравнения эллипса.
Расстояние между фокусами (фокусное расстояние) равно 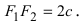
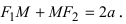
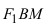
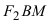
соответственно. Следовательно, согласно определению имеем
Возведем обе части равенства в квадрат, получим
Перенося квадратный корень в левую часть, а все остальное в правую часть равенства, находим 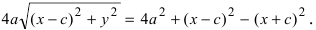
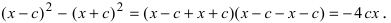
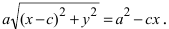
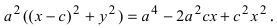
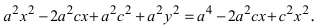
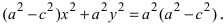
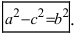
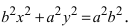
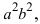
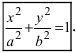
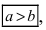
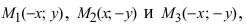
т.е. точками пересечения эллипса с осью абсцисс будут точки
т.е. точками пересечения эллипса с осью ординат будут точки
(Рис. 30).
Определение: Найденные точки называются вершинами эллипса.
Рис. 30. Вершины, фокусы и параметры эллипса
Определение: Если 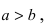
Определение: Эксцентриситетом эллипса называется отношение фокусного рас- стояния к большой полуоси эллипса
Из определения эксцентриситета эллипса следует, что он удовлетворяет двойному неравенству 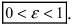
Если 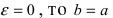
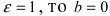
Пример:
Составить уравнение эллипса, если его большая полуось а = 5, а его эксцентриситет
Решение:
Исходя из понятия эксцентриситета, найдем абсциссу фокуса, т.е. параметр 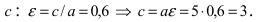
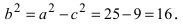
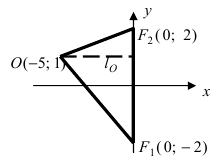
Пример:
Найти площадь треугольника, две вершины которого находятся в фокусах эллипса 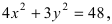
Решение:
Для определения координат фокусов эллипса и центра окружности преобразуем их уравнения к каноническому виду. Эллипс:
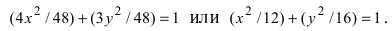
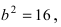
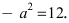
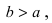
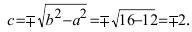
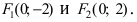
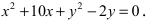
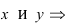
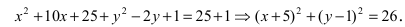
Построим в декартовой системе координат треугольник 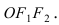
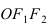
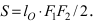
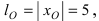
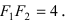
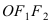
Видео:Эллипс (часть 8). Решение задач. Высшая математика.Скачать

Эллипс в высшей математике
где 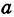
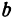
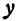
Отсюда видно, что уравнение (2) определяет две функции. Пока независимое переменное 
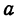

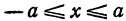
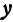
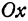
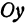
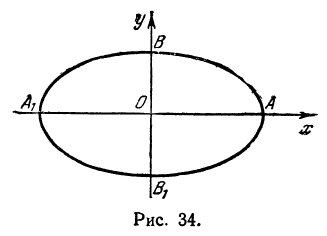
При 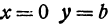
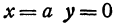
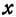

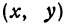
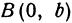
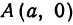
Полученная линия называется эллипсом. Число 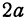
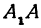
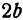
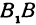
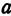
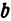
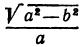
Пример:
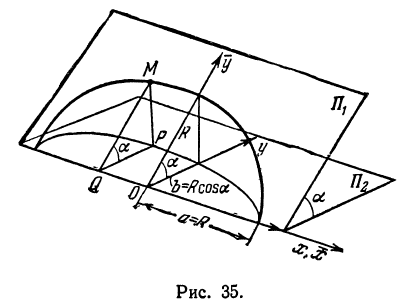
Найти проекцию окружности на плоскость, не совпадающую с плоскостью окружности.
Решение:
Возьмем две плоскости, пересекающиеся под углом 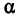
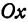
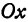
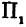
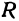
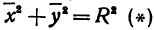
Пусть точка 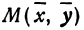
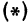
Обозначим проекцию точки 
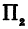
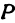
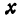
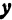


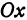
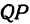
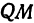
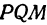
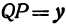
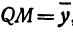
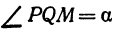
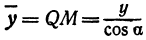


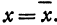
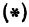
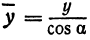
а это есть уравнение эллипса с полуосями 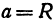
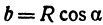
Таким образом, эллипс является проекцией окружности на плоскость, расположенную под углом к плоскости окружности.
Замечание. Окружность можно рассматривать как эллипс с равными полуосями.
Видео:Лекция 31.1. Кривые второго порядка. ЭллипсСкачать

Уравнение эллипсоида
Определение: Трехосным эллипсоидом называется поверхность, полученная в результате равномерной деформации (растяжения или сжатия) сферы по трем взаимно перпендикулярным направлениям.
Рассмотрим сферу радиуса R с центром в начале координат:
где Х, У, Z — текущие координаты точки сферы.
Пусть данная сфера подвергнута равномерной деформации в направлении координатных осей 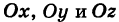
В результате сфера превратится в эллипсоид, а точка сферы М (X, У, Z) с текущими координатами Х, У, Z перейдет в точку эллипсоидам 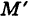
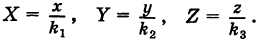
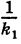
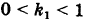
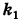
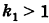
Подставляя эти формулы в уравнение (1), будем иметь
где 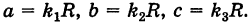
Величины 
Если две полуоси эллипсоида равны между собой, то эллипсоид называется эллипсоидом вращения, так как может быть получен в результате вращения эллипса вокруг одной из его осей. Например, в геодезии считают поверхность земного шара эллипсоидом вращения с полуосями
а = b = 6377 км и с = 6356 км.
Если а = b = с, то эллипсоид превращается в сферу.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Гипербола
- Парабола
- Многогранник
- Решение задач на вычисление площадей
- Шар в геометрии
- Правильные многогранники в геометрии
- Многогранники
- Окружность
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
📹 Видео
Поворот и параллельный перенос координатных осей. ЭллипсСкачать
Эллипс. Определение. Уравнение. График. Фокусы. Главные оси. Эксцентриситет - Новиков АлександрСкачать

§17 Определение эллипсаСкачать

Видеоурок "Приведение к каноническому виду"Скачать

Эллипс (часть 1). Каноническое уравнение. Высшая математика.Скачать

§28 Эксцентриситет эллипсаСкачать

Овчинников А. В. - Аналитическая геометрия - Эллипс, гипербола, параболаСкачать

Написать каноническое уравнение эллипса, если известны b и cСкачать

Полярные координаты. Полярное уравнение эллипса.Скачать

165. Найти фокусы и эксцентриситет эллипса.Скачать

Кривые второго порядка. Эллипс. Приведение к каноническому виду и чертежСкачать

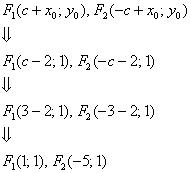
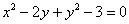
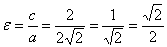

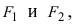
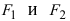
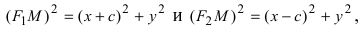
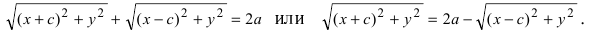
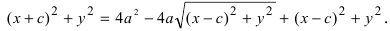
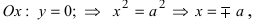 т.е. точками пересечения эллипса с осью абсцисс будут точки
т.е. точками пересечения эллипса с осью абсцисс будут точки 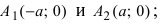
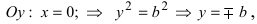 т.е. точками пересечения эллипса с осью ординат будут точки
т.е. точками пересечения эллипса с осью ординат будут точки 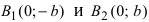 (Рис. 30).
(Рис. 30).