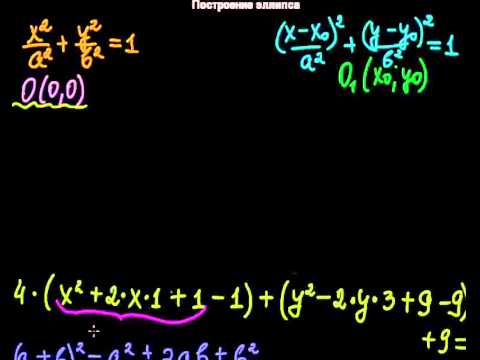Этот онлайн калькулятор позволит вам очень просто найти параметрическое и каноническое уравнение прямой проходящей через две точки.
Воспользовавшись онлайн калькулятором, вы получите детальное пошаговое решение вашей задачи, которое позволит понять алгоритм решения задач на составление уравнения прямой и закрепить пройденный материал.
Видео:ЭллипсСкачать

Найти уравнение прямой
Выберите необходимую вам размерность:
Введите координаты точек.
Ввод данных в калькулятор для составления уравнения прямой
В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
Дополнительные возможности калькулятора для составления уравнения прямой
- Используйте кнопки и на клавиатуре, для перемещения между полями калькулятора.
Теория. Уравнение прямой.
Прямая — один из базовых элементов геометрии. Используя уравнения прямых можно существенно упростить решение многих задач.
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Видео:§18 Каноническое уравнение эллипсаСкачать

Каноническое уравнение эллипса по двум точкам
| Две точки с координатами |
| Первая координата |
| Вторая координата |
| Каноническое уравнение эллипса |
| Большая полуось эллипса |
| Малая полуось эллипса |
| Эксцентриситет эллипса |
| Фокусное/фокальное расстояние |
| Коэффициент сжатия |
| Координаты первого фокуса F1(x1:y1) |
| Координаты второго фокуса F2(x2:y2) |
| Фокальный параметр |
| Перифокусное расстояние |
| Апофокусное расстояние |
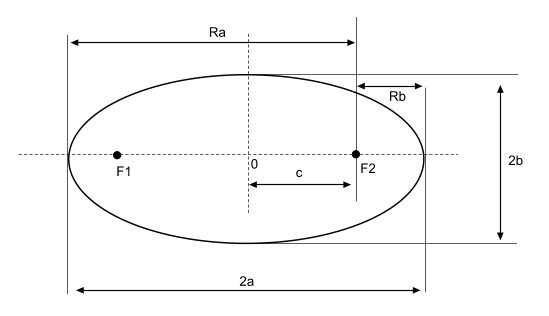
Уравнение эллипса в каноническом виде имеет вот такой вид.
Так как тут всего две переменных, то логично предположить, что по двум заданным точкам мы всегда сможем построить формулу эллипса.
Для расчета поставленной задачи воспользуемся материалом расчет кривой второго порядка на плоскости, который и позволит легко и быстро получить результат.
Кроме этого, на этой странице мы получим следующую информацию.
Фокальный параметр — половина длины хорды, проходящей через фокус и перпендикулярной большой оси эллипса
Значение полуосей — большая полуось и малая полуось ( Естественно это в том случае, когда эллипс вытянут вдоль оси абсцисс)
Эксцентриситет — коэффициент, показывающий насколько его фигура отличается от окружности
Фокальное расстояние
Коэффициент сжатия — отношение длин малой и большой полуосей
Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Примеры задач
Cоставить каноническое уравнение эллипса по двум точкам
Ввводим данные в калькулятор, не забывая что квадратный корень у нас обозначается sqrt
и получаем результат
| Каноническое уравнение эллипса | |||
| Большая полуось эллипса | |||
| Малая полуось эллипса | |||
| Эксцентриситет эллипса | |||
| Фокусное/фокальное расстояние | |||
| Коэффициент сжатия | |||
| Координаты первого фокуса F1(x1:y1) | |||
| Координаты второго фокуса F2(x2:y2) | |||
| Фокальный параметр | |||
| Перифокусное расстояние | |||
| Апофокусное расстояние | |||
И еще один пример Даны две точки с координатами (3:2) и (4:-9) построить каноническое уравнение эллипса. Если мы введем данные в калькулятор получим
|