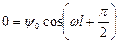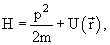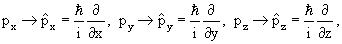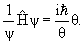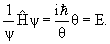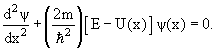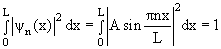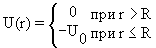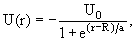Основной характеристикой состояния атомов, молекул, элементарных частиц является y-функция. Аналитическое выражение y-функции в каждом конкретном случае можно получить путем решения волнового уравнения – основного уравнения квантовой механики, предложенного Э. Шредингерам в 1920 г.
Применительно к стационарным состояниям уравнение Шредингера имеет вид:
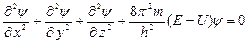
где т – масса частицы; Е и U – ее полная и потенциальная энергии.
Если частица перемещается только вдоль некоторой линии, например, вдоль оси ОХ (одномерный случай), то уравнение Шрёдингера упрощается и принимает вид:
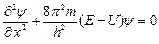
Одним из наиболее простых примеров использования уравнения Шрёдингера является решение задачи о движении частицы в одномерной потенциальной яме.
Физический смысл здесь имеет только одно значение:
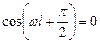
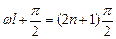
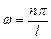
где п – целое число, оно принимает значения 1, 2, 3, . ; п ≠ 0, так как в противном случае y= 0 при любом х, что означает отсутствие электрона в потенциальной яме. Число n называют квантовым числом. Из (4.4) находим энергию 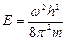
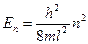
Индекс n при Е показывает, что различным значениям квантового числа n соответствует и разная энергия.
Подставляя w (4.7) в (4.5) и учитывая 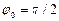
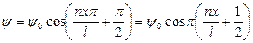
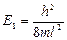
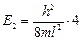
Возведя (4.9) в квадрат, получим плотность вероятности 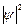
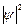
- Уравнение электрона в потенциальной яме
- 4.1. Уравнение Шредингера
- Уравнение Шредингера
- 4.2. Частица в одномерной прямоугольной яме с бесконечными стенками
- 4.3. Гармонический осциллятор
- Частица в одномерной потенциальной яме
- 4.4. Частица в поле с центральной симметрией
- 4.5. Орбитальный момент количества движения
- 4.6. Спин
- 4.7. Полный момент количества движения
- 4.8. Квантовые числа
- Таблица квантовых чисел
- Задачи
- Работа 6 СТАЦИОНАРНЫЕ СОСТОЯНИЯ ЭЛЕКТРОНА В ОДНОМЕРНЫХ ПОТЕНЦИАЛЬНЫХ ЯМАХ
- 💡 Видео
Видео:97. Микрочастица в потенциальной ямеСкачать

Уравнение электрона в потенциальной яме
Аналог классического волнового уравнения был предложен Э. Шредингером в 1925 г. Как и классическое уравнение, уравнение Шредингера связывает производные волновой функции по времени и координате. Уравнение Шредингера описывает поведение любых нерелятивистских систем. На примерах частицы, находящейся в бесконечно глубокой яме, и гармонического осциллятора рассмотрены простейшие квантовые системы, получены дискретные спектры состояний. Возможности описания динамики данных систем ограничены набором квантовых чисел, отражающих универсальные и внутренние симметрии квантовых систем.
4.1. Уравнение Шредингера
В квантовой физике изменение состояния частицы описывается уравнением Шредингера
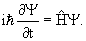 | (4.1) |
где 
в которой 







х → 


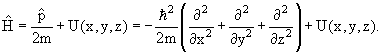 | (4.2) |
Уравнение Шредингера
Зависящее от времени уравнение Шредингера:
где 
Разделение переменных. Запишем Ψ(




Левая часть является функцией только координат, а правая не зависит от переменной x. Поэтому обе части последнего уравнения должны быть равны одной и той же постоянной, которую обозначим E
θ(t) = exp(−iEt/ћ), 




Уравнение 


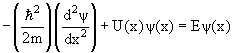
Для трехмерной системы с массой m в поле с потенциалом U(
−(ћ 2 /2m)Δψ(



где Δ – лапласиан.
Так как уравнение Шредингера является линейным уравнением первого порядка по времени, то с его помощью по заданному значению волновой функции Ψ(x, y, z, 0) в момент времени t = 0 можно найти её значение в произвольный момент времени t − Ψ(x, y, z, t).
Уравнение Шредингера для стационарного состояния, когда потенциальная энергия частицы не зависит от времени, имеет вид
 ψ( ψ( ) = Eψ( ) = Eψ( ). ). | (4.3) |
Это уравнение называют стационарным уравнением Шредингера.
Так как в стационарном состоянии
Ψ( ,t) = ψ( ,t) = ψ( )exp(−iEt/ћ) )exp(−iEt/ћ) | (4.4) |
и вероятность найти частицу в момент t в точке x, y, z пропорциональна |Ψ(
|ψ(x,y,z)| 2 , т.е. не зависит от времени. Аналогично, вероятность обнаружить значение физической величины, характеризующей систему, также не изменяется со временем, поскольку выражается через квадрат модуля волновой функции.
4.2. Частица в одномерной прямоугольной яме с бесконечными стенками
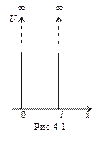
Потенциальная энергия U(x) в прямоугольной яме удовлетворяет следующим условиям:
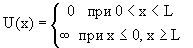 | (4.5) |
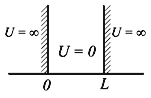
Рис.4.1. Прямоугольная яма с бесконечными стенками
Частица находится в области 0 ≤ x ≤ L. Вне этой области ψ(x) = 0. Уравнение Шредингера для частицы, находящейся в области 0 ≤ x ≤ L
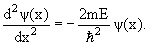 | (4.6) |
Волновая функция, являющаяся решением уравнения (4.9), имеет вид
| ψ(x)= Аsin kx + Bcos kx, | (4.7) |
где k = (2mE/ћ 2 ) 1/2 . Из граничных условий ψ(0) = 0, ψ(L) = 0 и условий непрерывности волновой функции следует
| Аsin kL = 0. | (4.8) |
kL = nπ, n = 1, 2, 3, … , то есть внутри потенциальной ямы с бесконечно высокими стенками устанавливаются стоячие волны, а энергия состояния частиц имеет дискретный спектр значений En
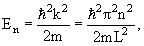 n = 1, 2, 3, … n = 1, 2, 3, … | (4.9) |
Частица может находиться в каком-то одном из множества дискретных состояний, доступных для неё.
Каждому значению энергии En соответствует волновая функция ψn(x), которая с учетом условия нормировки
 | (4.10) |
В отличие от классической, квантовая частица в прямоугольной яме не может иметь энергию
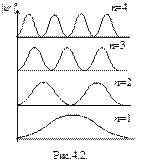
E 2 π 2 /(2mL 2 ). Состояния частицы ψn в одномерном поле бесконечной потенциальной ямы полностью описывается с помощью одного квантового числа n. Спектр энергий дискретный.
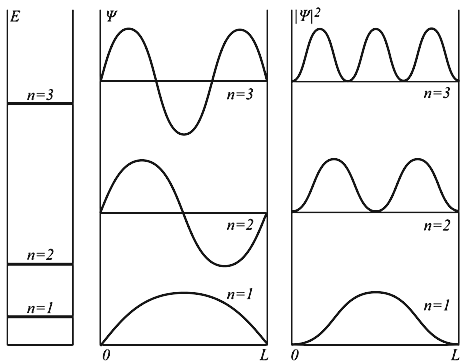
Рис. 4.2. Уровни энергии и волновые функции частицы Ψ в бесконечной прямоугольной яме. Квадрат модуля волновой функции |Ψ| 2 определяет вероятность нахождения частицы в различных точках потенциальной ямы.
4.3. Гармонический осциллятор
Положение уровней частицы в потенциальной яме зависит от вида потенциальной ямы. В одномерной потенциальной яме гармонического осциллятора потенциальная энергия имеет вид
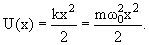 | (4.11) |
В этом случае одномерное уравнение Шредингера имеет вид
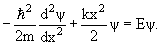 | (4.12) |
Допустимые значения полной энергии определяются формулой
| En = ћω0(n + 1/2), n = 0, 1, 2, | (4.13) |
В отличие от бесконечной прямоугольной ямы, спектр уровней гармонического осциллятора эквидистантный.
С увеличением массы частицы или размеров области ее локализации квантовое описание частицы переходит в классическое.
Частица в одномерной потенциальной яме
Одномерная прямоугольная яма шириной L:
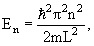

Одномерный гармонический осциллятор:
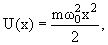
4.4. Частица в поле с центральной симметрией
В сферических координатах стационарное уравнение Шредингера для частицы в центральном потенциале U(r) имеет вид
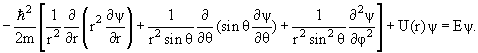 | (4.14) |
Решение уравнения (4.14) записываются в виде произведения радиальной и угловой функций
| ψ(r,θ,φ) = Rnl(r)Ylm(θ,φ), | (4.15) |
где радиальная функция Rnl(r) и угловая функция Ylm(θ,φ), называемая сферической, удовлетворяют уравнениям
 2 Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) 2 Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) | (4.16) |
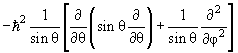 Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) 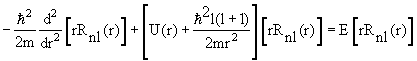 | (4.17) |
Уравнение (4.16) определяет возможные собственные значения l и собственные функции Ylm(θ,φ) оператора квадрата момента 
Схема уровней (последовательность и абсолютные значения энергий) зависит от радиальной функции Rnl(r), которая в свою очередь определяется потенциалом U(r), в котором находится частица.
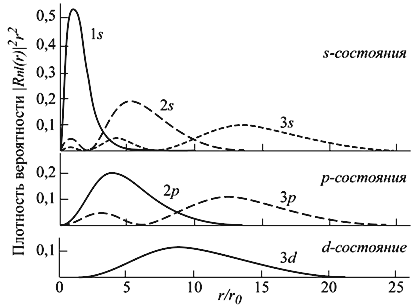
Рис. 4.3. Радиальное распределение вероятности нахождения электрона в кулоновском поле протона (атом водорода). Расстояния даны в боровских радиусах
r0 = ћ 2 /mee 2 ≈ 0.529·10 8 cм.
| Решения уравнения |
существуют лишь при определенных значениях квантовых чисел n (радиальное квантовое число), l (орбитальное квантовое число) и m (магнитное квантовое число).
Возможные энергетические состояния системы (уровни энергии) определяются числами n и l и в случае сферически симметричных состояний не зависят от квантового числа m. Число n может быть только целым:
n = 1, 2, …, ∞. Число l может принимать значения 0, 1, 2, …, ∞.
4.5. Орбитальный момент количества движения
Собственные значения L 2 и Lz являются решением уравнений


Они имеют следующие дискретные значения
L 2 = ћ 2 l(l + 1), где l = 0, 1, 2, 3, …,
Lz = ћm, где m = 0, ± 1, ± 2, ± 3,…, ± l.
Для характеристики состояний с различными значениями орбитального момента l обычно используют следующие обозначения:
Спектроскопические названия орбитальных моментов l
| l = 0 | s-состояние |
| l = 1 | p-состояние |
| l = 2 | d-состояние |
| l = 3 | f-состояние |
| l = 4 | g-состояние |
| l = 5 | h-состояние |
| и. т. д. |
Состоянию с l = 0 отвечает сферически симметричная волновая функция. В тех случаях, когда l ≠ 0 волновая функция не имеет сферической симметрии. Симметрия волновой функции определяется симметрией сферических функций Ylm(θ,φ). Имеет место интересное квантовое явление, когда решение сферически симметричной задачи (потенциал описывает сферически симметричную систему) приводит к состояниям, не обладающим сферической симметрией. Таким образом, симметрия уравнений не обязательно должна отражаться в симметрии каждого отдельно взятого решения этих уравнений, а лишь во всей совокупности этих решений.
Для частицы, находящейся в сферически симметричном потенциале, величина орбитального момента количества движения L:
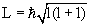 | (4.18) |
Обычно, для упрощения, когда говорят о величине орбитального момента количества движения, называют этой величиной квантовое число l, имея в виду, что между l и L имеется однозначная связь (4.18).
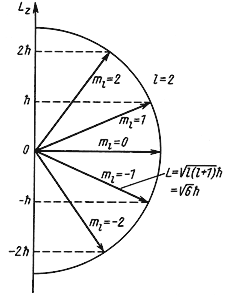
Рис. 4.4 Возможные ориентации вектора 
Так как величина l может принимать только целочисленные значения 0, 1, 2, 3,…, то и орбитальный момент количества движения L квантуется. Например, для частицы с l = 2 момент количества движения
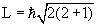
= 6.58·10 -22 √6 МэВ·сек ≈ 2.6·10 — 34 Дж·сек.
Пространственное квантование. Орбитальный момент количества движения является векторной величиной. Так как величина орбитального момента количества движения квантуется, то и направление 

Состояние частицы, находящейся в сферически симметричном поле, полностью описывается тремя квантовыми числами: n, l и m.
Появление квантовых чисел связано со свойствами симметрии системы. Характер этой симметрии определяет возможные значения квантовых чисел. Очевидно, что система, описываемая функцией e im φ , примет прежнее значение только тогда, когда азимутальный угол φ в результате поворота вокруг оси z примет прежнее значение φ. Этому условию функция e im φ удовлетворяет только в случае, когда величина mφ кратна 2π. Т.е. величина m должна иметь целые значения. Так как необходимо учитывать вращение в двух противоположных направлениях и отсутствие вращения, единственно возможными значениями оказываются m = 0, ±1, ±2, … .
4.6. Спин
Спин − собственный момент количества движения частицы. Между значением вектора спина 

 2 = ћ 2 s(s + 1) 2 = ћ 2 s(s + 1) | (4.19) |
В отличие от орбитального квантового числа l, которое может быть лишь целым числом или нулем, спиновое квантовое число s (в дальнейшем просто спин) может быть как целым (включая нуль), так и полуцелым, т. е. s = 0, 1/2, 1, 3/2, 2, 5/2, … , но при этом для каждой элементарной частицы спин может принимать единственное присущее этому типу частиц значение. Так, спины π-мезонов и К-мезонов равны 0. Спины электрона, протона, нейтрино, кварков и их античастиц равны 1/2. Спин фотона равен 1. Бозоны составляют класс частиц с целым значением спина, спин фермионов имеет полуцелое значение. Спин частицы невозможно изменить, также как её заряд или массу. Это её неизменная квантовая характеристика.
Как и в случае других квантовых векторов, проекция вектора спина 
szћ = ±sћ, ±(s − 1)ћ, ±(s − 2)ћ. ±1/2ћ или 0.
Число sz − это квантовое число проекции спина. Максимальная величина sz совпадает с s. Так как спин электрона равен 1/2, то проекция этого спина может принимать лишь два значения sz = ±1/2. Если проекция +1/2, то говорят, что спин направлен вверх, если проекция -1/2, то говорят, что спин направлен вниз.
4.7. Полный момент количества движения
Полный момент количества движения частицы или системы частиц 





Квадрат полного момента имеет значение:

Квантовое число полного момента j, соответствующее сумме двух векторов 

j = l + s, l + s −1. |l − s|
Проекция 
Число значений проекции Jz равно 2j + 1. Если для 

4.8. Квантовые числа
Квантовые числа – это целые или дробные числа, которые определяют все возможные значения физической величины, характеризующей различные квантовые системы – атомы, атомные ядра, кварки и другие частицы.
Таблица квантовых чисел
| n | Радиальное квантовое число. Определяет число узлов волновой функции и энергию системы. n = 1, 2, …, ∞. |
| J, j | Полный угловой момент J и его квантовое число j. Последнее никогда не бывает отрицательным и может быть целым или полуцелым в зависимости от свойств рассматриваемой системы.  2 = ћ 2 j(j + 1). 2 = ћ 2 j(j + 1). |
| L, l | Орбитальный угловой момент L и его квантовое число l. Интерпретация l такая же, как j, но l может принимать только целые значения, включая нуль: l = 0, 1, 2,…. L 2 = ћ 2 l(l + 1). |
| m | Магнитное квантовое число. Проекция полного или орбитального углового момента на выделенную ось (обычно ось z) равна mћ. Для полного момента m = ±j, ±(j-1), …, ±1/2 или 0. Для орбитального m = ± l, ± (l-1), …, ±1, 0. |
| S, s | Спиновый угловой момент S и его квантовое число s. Оно может быть либо положительным целым (включая нуль), либо полуцелым. s – неизменная характеристика частицы определенного типа. S 2 = ћ 2 s(s + 1). |
| sz | Квантовое число проекции спинового момента частицы на выделенную ось. Эта проекция может принимать значения szћ, где sz = ± s, ± (s -1), …, ±1/2 или 0. |
| P или π | Пространственная четность. Характеризует поведение системы при пространственной инверсии  → — → —  (зеркальном отражении). Полная четность частицы Р = π(-1) l , где π – её внутренняя четность, а (-1) l – её орбитальная четность. Внутренние четности кварков положительные, антикварков — отрицательные. (зеркальном отражении). Полная четность частицы Р = π(-1) l , где π – её внутренняя четность, а (-1) l – её орбитальная четность. Внутренние четности кварков положительные, антикварков — отрицательные. |
| I | Изоспин. Характеризует свойство зарядовой инвариантности сильных взаимодействий |
Для обозначения спинового момента часто используют букву J.
Все состояния, в которых может находиться квантовая система, описываются с помощью полного набора квантовых чисел. Так в случае протона в ядре состояние протона описывается с помощью четырех квантовых чисел, соответствующих четырем степеням свободы – трем пространственным координатам и спину. Это
- Радиальное квантовое число n ( 1, 2, …, ∞),
- Орбитальное квантовое число l (0, 1, 2, …),
- Проекция орбитального момента m (± l, ± (l-1), …, ±1, 0),
- Спин протона s =1/2.
Для описания сферически-симметричных систем в квантовой физике используются различные сферически симметричные потенциалы с различной радиальной зависимостью:
- Кулоновский потенциал U = Q/r,
- Прямоугольная потенциальная яма
- Потенциал типа гармонического осциллятора U = kr 2 ,
- Потенциал Вудса-Саксона (с его помощью описываются внутриядерные взаимодействия):
где U0, а и R – положительные константы (R – радиус ядра). Во всех случаях сферически симметричные системы можно описать с помощью набора квантовых чисел n, l, j, jz, однако, в зависимости от радиального вида потенциала энергетический спектр состояний системы будет различным.
Существование сохраняющихся во времени физических величин тесно связано со свойствами симметрии гамильтониана системы. Например, в случае, если квантовая система обладает центральной симметрией U = U(r), то этой системе соответствует сохранение орбитального момента количества движения l и одной из его проекций m. При этом из-за сферической симметрии задачи энергия состояний не будет зависеть от величины m, т. е. состояния будут вырожденными по m.
Наряду с пространственными симметриями, связанными с непрерывными преобразованиями, в квантовой физике существуют и другие симметрии – дискретные. Одной из них является зеркальная симметрия волновой функции относительно инверсии координат (

Система тождественных частиц характеризуется еще одной симметрией – симметрией относительно перестановок тождественных частиц. Эта симметрия определяется свойствами частиц, образующих систему. Системы частиц с целым спином (бозонов) описываются симметричными волновыми функциями, системы частиц с полуцелым спином (фермионов) − антисимметричными волновыми функциями.
Задачи
4.1. Вычислите допустимые уровни энергии электрона, находящегося в одномерной прямоугольной потенциальной яме шириной 10 -8 см, протона, находящегося в потенциальной яме 5 Фм, и шарика массой 1 г, находящегося в потенциальной яме 1 см.
4.2. Рассчитать энергию перехода между состояниями 1s и 2s в атоме водорода.
4.3. Найти значение полного момента j для протона в d-состоянии. Каким будет результат измерения полного момента протона в состоянии 1d5/2?
4.4. Найти полный момент (квантовое число j) системы двух нуклонов в s‑состоянии (l = 0).
4.5. Какие значения может иметь полный момент системы j, если
А. Нейтрон и протон находятся в состояниях с |l,s:j>n = |1, 1 /2: 3 /2>, |l,s:j>p = |1, 1 /2: 3 /2>?
Б. Два нейтрона находятся в состояниях с |l,s:j>1 = |1, 1 /2: 3 /2> и |l,s:j>2 = |1, 1 /2: 3 /2>?
4.6. А) Нейтрон находится в p-состоянии. Найти значения полного момента j и возможные значения проекции момента jz. Каким будет результат измерения орбитального момента частицы в этом состоянии? Б) Рассмотрите задачу А) для протона в d-состоянии.
Ответ: А) j = 3/2, 1/2; jz = ±3/2, ±1/2; L = ћ√ l(l +1) = √ 2 ћ;
Б) j = 5/2, 3/2; jz = ±5/2, ±3/2, ±1/2; L = ћ√ l(l +1) = √ 6 ћ
4.7. А) Частица с собственным моментом s = 3/2 находится в состоянии с орбитальным моментом
l = 2. Найти полный момент частицы j.
Б) Частица с собственным моментом s = 1/2 находится в состоянии с орбитальным моментом
l = 3. Определите полный момент частицы j
Ответ: А) j = 7/2 ÷ 1/2; Б) j = 7/2, 5/2
4.8. Протон и нейтрон находятся в состоянии с относительным орбитальным моментом L = 1. Найти полный момент системы J.
Ответ: J = 0, 1, 2
4.9. На оболочке с квантовым числом n = 1, l = 2 находятся протон и нейтрон. Определить их суммарный полный момент J и его проекцию Jz. Изменится ли результат, если на оболочке n = 1,
l = 2 будут находиться два нейтрона?
4.10. Почему возникают вырожденные состояния?
4.11. Написать оператор Гамильтона 
4.12. Напишите стационарное уравнение Шредингера в сферической системе координат.
4.13. Какие квантовые числа характеризуют частицу в центрально-симметричной потенциальной яме?
4.14. Покажите, что волновые функции ψ = Aexp(kx −ωt) и ψ = Asin(kx −ωt) не удовлетворяют зависящему от времени уравнению Шредингера.
4.15. Покажите, что волновые функции ψ = Ae i(kx −ωt) и ψ = A(cos(kx −ωt) − sin(kx −ωt))удовлетворяют зависящему от времени уравнению Шредингера.
4.16. Частица находится в низшем состоянии n = 1 в бесконечно глубокой одномерной прямоугольной потенциальной яме размера L.
А) Рассчитайте вероятность обнаружить частицу в интервале Δx = 0.001L при x = 1 /2L, x = 2 /3L, x = L.
Б) Рассмотрите случай, когда частица находится в состоянии n = 2 при тех же значениях x.
Ответ: А) P(L/2) = 0.002; P(2L/3) = 0.0015; P(L) = 0; Б) P(L/2) = 0; P(2L/3) = 0.0015; P(L) = 0
4.17. Частица находится в состоянии n = 2 в бесконечно глубокой одномерной прямоугольной потенциальной яме размера L. Рассчитайте вероятность обнаружить частицу в интервале ( 1 /3L, 2 /3L).
Ответ: P(L/3, 2L/3) = 0.2
4.18. Электрон находится всостонии n = 5 в бесконечно глубокой одномерной прямоугольной потенциальной яме размера L. Рассчитайте вероятность обнаружить электрон в области x от 0.2L до 0.5L.
Ответ: P(0.2L, 0.5L) = 0.3
4.19. Электрон находится в бесконечно глубокой одномерной потенциальной яме. Рассчитайте ширину потенциальной ямы, если энергия состояния n = 1 равна 0.1 эВ.
Ответ: L = 1.9 нм
4.20. Рассчитайте средние значения и 2 > для состояний n = 1, 2, 3 в бесконечно глубокой прямоугольной потенциальной яме.
4.21. Что общего и в чем различие в описании атома водорода в теории Шредингера и в модели Бора?
4.22. Почему энергии атома водорода в теории Шредингера не зависят от орбитального квантового числа l?
4.23. Угловой момент характеризуется квантовым числом l = 3. Какие значения могут принимать Lz и L 2 ?
Ответ: Lz = -3ћ, -2ћ. 3ћ; L 2 = 12ћ 2
4.24. Угловой момент характеризуется квантовым числом l = 3. Какие значения могут принимать Lz и L 2 ?
Видео:Волновая функция (видео 5) | Квантовая физика | ФизикаСкачать

Работа 6 СТАЦИОНАРНЫЕ СОСТОЯНИЯ ЭЛЕКТРОНА В ОДНОМЕРНЫХ ПОТЕНЦИАЛЬНЫХ ЯМАХ
Цель работы Численное решение одномерного стационарного уравнения Шредингера на компьютере, отбор физически приемлемых решений, изучение влияния формы и параметров потенциальной ямы на уровни энергии и волновые функции связанных состояний.
6.1 Уравнение Шредингера и его решения
Стационарное уравнение Шредингера является уравнением на собственные значения оператора Гамильтона

Где для одномерных задач

Таким образом, волновая функция Ψ(X) согласно (6.1) и (6.2) удовлетворяет дифференциальному уравнению второго порядка:

Здесь 
Специфика конкретной физической задачи заключена в потенциальной функции U(X) . Иначе говоря, одна физическая задача отличается от другой видом потенциальной функции U(X), включаемой в уравнение Шредингера.
Решить дифференциальное уравнение Шредингера – это значит найти множество удовлетворяющих ему волновых функций Ψ(X) . В принципе, уравнение Шредингера может быть решено при любых значениях полной энергии Е, но не все такие математические решения физически приемлемы. Поэтому условие физической приемлемости является существенной частью каждой рассматриваемой задачи. Физический смысл имеют лишь те решения, для которых волновая функция Ψ(X) является Однозначной, Ограниченной, Непрерывной и гладкой. В частности, требование ограниченности связано с Вероятностной интерпретацией волновой функции, согласно которой выражение 

Значения энергии E, при которых стационарное уравнение Шредингера имеет физически приемлемые решения, – уровни энергии– являются собственными значениями оператора Гамильтона. Соответствующие волновые функции являются Собственными функциями этого оператора.
Можно доказать, что в случае Финитного (ограниченного) движения энергия Е не может быть произвольной, т. е. спектр энергии оказывается дискретным. Случай финитного движения соответствует связанной частице, например, электрону в атоме или нуклону в ядре. В то же время при Инфинитном движении физически приемлемые решения стационарного уравнения Шредингера получаются для некоторого непрерывного интервала значений энергии Е, так что спектр энергии оказывается сплошным. Инфинитное движение, в частности, совершает электрон, оторванный от атома в результате ионизации.
Таким образом, из уравнения Шредингера естественно вытекает важнейшая особенность поведения атомных систем, резко отличающая их от систем, подчиняющихся законам классической механики: Существование дискретных уровней энергии.
Отметим также, что волновые функции стационарных состояний, принадлежащих дискретному спектру энергии, можно нормировать на единицу, т. е. путем умножения на нормировочный множитель добиться выполнения условия нормировки вида

6.2 Линейный гармонический осциллятор
Как известно, в классической механике частица массы M, находящаяся в силовом поле с потенциальной энергией

При любом значении E > 0 совершает гармонические колебания с частотой

Постоянная K носит название Коэффициента упругости или Коэффициента жесткости.
Согласно квантовой механике поведение частицы в тех же условиях определяется уравнением Шредингера. Для стационарных состояний линейного гармонического осциллятора в соответствии с (6.3) и (6.5) оно имеет вид:

Данное уравнение имеет точное аналитическое решение. Для собственных значений энергии получается простая формула:


Собственные функции ΨN, к которым приводит аналитическое решение, представляют собой произведение функции Гаусса exp(-Y2/2) на полиномы Чебышева–Эрмита N-й степени Pn(Y):
Здесь введено обозначение Y=(Mω/ħ2)1/2X , а Cn есть нормирующий множитель. Для первых трех состояний полином Pn(Y) имеет вид
Гауссов сомножитель обеспечивает стремление волновой функции к нулю при возрастании X. Полином Pn(Y) имеет N корней, следовательно, столько же узлов имеет волновая функция. Таким образом, волновая функция колеблется внутри классически разрешенной области, т. е. при (E>U), и затухает по гауссову закону в классически запрещенной области, где (E A) экспоненциально убывает по мере удаления от стенки:
ΨN(X)=BnExp(-κN X ), где 
Здесь Bn является нормирующим множителем. Это означает, что происходит проникновение связанной частицы в классически запрещенную область. Глубину проникновения δ можно определить как расстояние от стенки, на котором плотность вероятности нахождения частицы уменьшается в Е=2,718… раз. Тогда для δ получается выражение

Таким образом, глубина проникновения оказывается тем большей, чем меньше отстоит соответствующий энергетический уровень от верха потенциальной ямы. Фактически происходит увеличение эффективной ширины ямы LЭфф :
Подставляя в формулу (6.9б) LЭфф вместо L, можно приближенно найти собственные значения энергии En в потенциальной яме конечной глубины. Из-за того что LЭфф > L,, значения En уменьшатся. Следовательно, уровни энергии в яме конечной глубины должны лежать ниже соответствующих уровней бесконечно глубокой ямы, а их понижение тем значительнее, чем больше номер уровня.
Результаты компьютерных решений (при ħ=M=1) легко распространить на «реальные» прямоугольные ямы. Это можно сделать, в частности, на основе сопоставления формул (6.9б) и (6.9в).
Часть полученных результатов будет относиться также к асимметричной потенциальной яме половинной ширины, но с бесконечно высокой левой стенкой (рис. 6.2). Очевидно, волновая функция должна обращаться в нуль на этой стенке (т. е. при X=0). Следовательно, граничным условиям на левой стенке удовлетворяют лишь решения с нечетными волновыми функциями для симметричной ямы. Им соответствуют уровни энергии с четными номерами. Именно эти состояния и реализуются в асимметричной яме.
В отличие от симметричной ямы, для которой всегда есть хотя бы одно связанное состояние, асимметричная яма не может удержать частицу, если ее глубина меньше некоторого критического значения UКр. Критическую глубину можно найти из условия, что при этом E=U0=UКр, а на ширине ямы размещается четверть длины волны де Бройля

Отсюда для критической глубины следуют выражения в обычных и условных единицах:


Одномерная асимметричная потенциальная яма с бесконечно высокой стенкой представляет непосредственный практический интерес, поскольку к ней сводятся некоторые трехмерные задачи, моделирующие движение частицы в центральном силовом поле (например, задача о дейтроне).
6.4 Решение уравнения Шредингера
С помощью компьютера
В данной работе с помощью компьютера реализуется численное решение стационарного уравнения Шредингера. Следует отметить, что численный метод решения является универсальным и может быть осуществлен для любой потенциальной функции, в то время как аналитически решаются лишь немногие задачи.
Численное решение проводится в такой системе единиц, в которой «перечеркнутая» постоянная Планка и масса частицы полагаются равными единице, т. е.
В этих единицах стационарное уравнение Шредингера принимает вид

При заданных массе частицы M, потенциальной энергии U(X), полной энергии E и определённых граничных условиях, т. е. при выборе численных значений волновой функции Ψ(X) и её производной 
На компьютере с помощью соответствующих численных методов можно найти функцию Ψ(X) в достаточно большом интервале значений X, аппроксимирующую (с требуемой точностью) непрерывное, гладкое, однозначное решение уравнения Шредингера.
Существенно, однако, что при произвольно выбранных граничных значениях волновой функции Ψ1 , её производной Ψ′1 и полной энергии E Эти решения будут практически всегда неограниченно растущими при X → ∞ или при X → – ∞ .
Можно строго доказать, что в случае финитного движения в симметричной потенциальной яме U(X) = U(–X) все физически приемлемые решения уравнения Шредингера будут либо чётными Ψ(X) = Ψ(–X) , либо нечётными Ψ(X) = – Ψ(–X) . Это делает возможным (и удобным практически) использование следующих граничных условий:
Ψ(X) = Ψ0, Ψ´(X) = 0 (для чётных решений),
Ψ(X) = 0, Ψ´(X) = Ψ´0 (для нечётных решений).
После этого ограниченность или расходимость Ψ(X) будет всецело зависеть от полной энергии E.
Программа позволяет визуализировать процесс поиска физически приемлемых решений уравнения Шредингера и спектра энергии. В окне вывода отображаются:
– положение уровня полной энергии E (на фоне кривой U(X) ),
– графики волновых функций Ψ(X) или их квадратов |Ψ(X)|2, построенные с использованием уровней энергии E в качестве осей абсцисс.
Оси абсцисс имеют градуировку, позволяющую определять протяженность тех или иных участков на графиках. Цена деления в градуировке составляет 0,1 условной единицы длины.
Поиск физически приемлемых решений состоит в нахождении методом проб и ошибок таких значений энергии E, при которых график волновой функции не расходится в заданных пределах изменения координаты. Существенно, что при отклонении E от собственного значения в большую или меньшую сторону волновая функция расходится (т. е. неограниченно возрастает) в разных направлениях (вверх либо вниз). В процессе поиска собственных значений энергии (или уровней энергии) находят «вилку», т. е. такие два значения E, при которых волновая функция будет расходиться в разных направлениях. Ширину этой «вилки» сужают настолько, чтобы она сравнялась с требуемой точностью собственного значения E .
Чтобы перейти к выполнению лабораторной работы, необходимо ответить на несколько Проверочных вопросов.. Если вы ответили неправильно хотя бы на один вопрос, то вы не сможете выполнять работу до тех пор, пока не найдете и не исправите ошибку.
Программа может работать в Двух режимах: ручном и автоматическом. Параметры потенциальных ям могут быть введены или изменены только в ручном режиме. В Ручном режиме, наблюдая за ходом графика волновой функции, путем проб и ошибок находят «вилку», т. е. два значения энергии, между которыми лежит собственное значение E, а затем сужают эту «вилку» до требуемой точности. В Автоматическом режиме программа, действуя по тому же принципу, сама находит все собственные значения энергии E и строит соответствующие им волновые функции. Найденные собственные значения энергии выводятся в таблицу.
Чтобы автоматический режим стал доступен, нужно найти три уровня энергии E в ручном режиме. Ввод параметров новых потенциальных ям может быть выполнен только в ручном режиме. При этом сохраняется возможность проведения вычислений и в автоматическом режиме.
Результаты компьютерных решений, проведенных при ħ=M=1, легко пересчитать на прямоугольные ямы, параметры которых заданы в размерных единицах. Пересчет можно сделать, в частности, на основе сопоставления формул (6.9б) и (6.9в).
Для ввода значения энергии E следует набрать некоторое вещественное число и нажать клавишу “Enter”. Аналогично осуществляется ввод остальных параметров.
Меню “Настройки” состоит из команд:
– “Квадрат волновой функции” – строит графики квадрата волновой функции;
– “Сравнить с бесконечно глубокой ямой” – отображает две ямы: конечной и бесконечной глубины вместе с волновыми функциями (команда доступна только в автоматическом режиме );
– “Сравнить с ямами удвоенной глубины и ширины” – отображаются три ямы вместе с волновыми функциями для сравнения (команда доступна только в автоматическом режиме );
– “Размещать окно в экране” – позволяет изменять размеры окна вывода следующей за ней командой;
– “Размеры окна” – изменяет размер окна;
– “Масштабировать на всё окно” – при снятии флажка с этой команды изображение будет выводиться на экран с фиксированным коэффициентом масштабирования по вертикали.
Меню “Работа” позволяет осуществлять переход между частями лабораторной работы. Ко второй части («Прямоугольная потенциальная яма») можно переходить лишь после выполнения первой части («Линейный гармонический осциллятор»).
1. Для линейного гармонического осциллятора с заданным коэффициентном жесткости K (значение K задает преподаватель) найдите уровни энергии и волновые функции основного и нескольких ближайших к нему возбуждённых состояний. (Сначала нужно в ручном режиме найти три значения энергии, при которых волновая функция не расходится, после чего остальные уровни можно найти в автоматическом режиме.)
Используя градуировку осей абсцисс на экране компьютера, определите длину ΔXn участка графика Ψ2(X) в классически запрещенной области (до его касания с осью X). Проделайте это для всех уровней энергии.
Сравните найденные собственные значения En´ с рассчитанными по формуле (6.8)

Положив в ней 
💡 Видео
Урок 456. Движение микрообъекта в одномерной бесконечно глубокой потенциальной ямеСкачать

Частица в одномерной потенциальной ямеСкачать

Туннельный эффектСкачать

Классические уравнения | одномерное стационарное уравнение Шрёдингера | беск. потенц. яма | 1Скачать

Частица в одномерной потенциальной ямеСкачать

Урок 455. Уравнение ШрёдингераСкачать

1-D finite Square Well/Электрон в одномерной потенциальной яме конечной глубиныСкачать

Рубцов А. Н. - Введение в квантовую физику - Частица в потенциальной ямеСкачать

Урок 459. Обзор квантовой теории атома водородаСкачать

Движение частицы в потенциальной яме.Скачать

Квантовая механика 41 - Уравнение Шредингера. Гамильтониан.Скачать

Урок 454. Понятие о волновой функцииСкачать

Атомная и ядерная физика. Лекция 7. Уравнение Шрёдингера. Частица в потенциальной яме.Скачать

Волна де Бройля (видео 4) | Квантовая физика | ФизикаСкачать
Воронина Е. Н. - Атомная физика. Семинары - Решение уравнения Шредингера для потенциальной ямыСкачать

7.2 Квантовая ямаСкачать

Семинар 7. Стационарное уравнение Шредингера. Состояния дискретного спектра. Потенциальные ямы.Скачать

потенциальная яма 1 | одномерные задачи | задачи по квантовой механикеСкачать