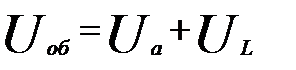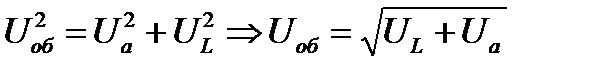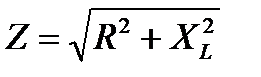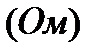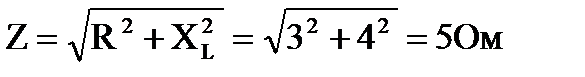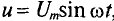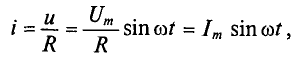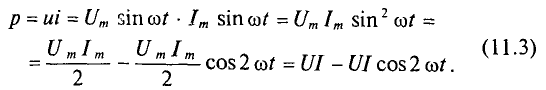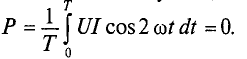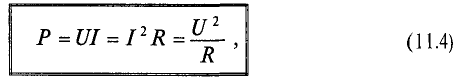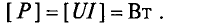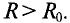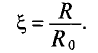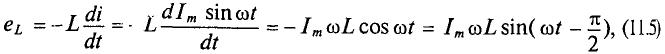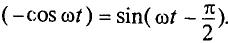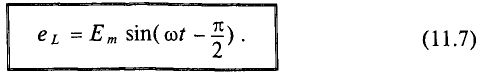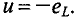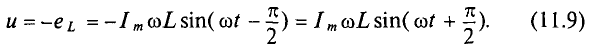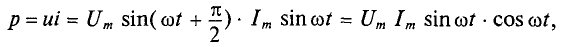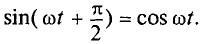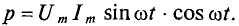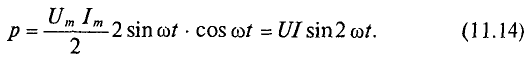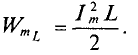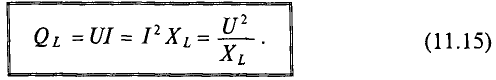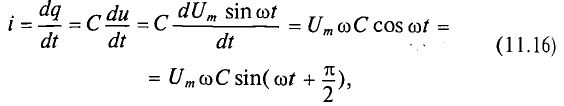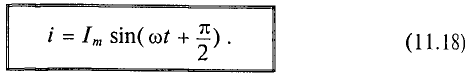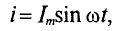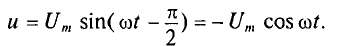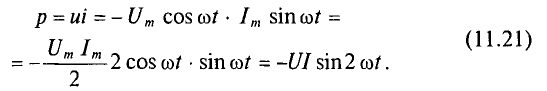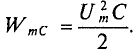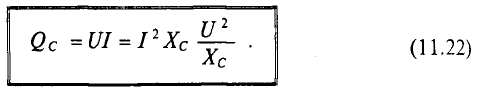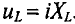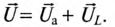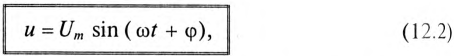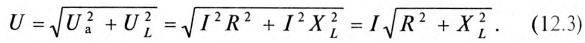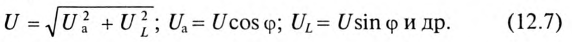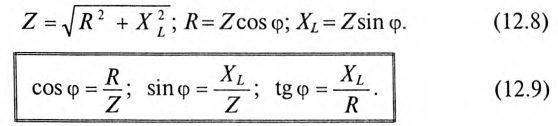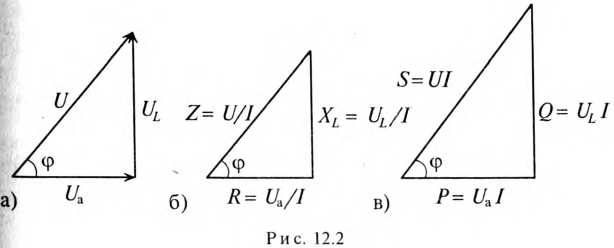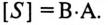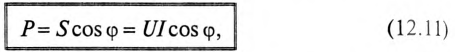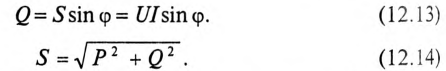Уравнение электрического состояния цепи с резистором и катушкой индуктивности

Видео:Урок 359. Конденсатор и катушка индуктивности в цепи переменного тока.Скачать

Последовательное соединение резистора и индуктивности

(цепочка RL )

Ранее была рассмотрена идеальная катушка индуктивности, где мы учитывали только один параметр – индуктивность катушки. Для реальной катушки индуктивности приходится учитывать не только её индуктивность L, но и сопротивление R – провода, которыми она намотана. К реальным катушкам индуктивности относятся, например, обмотки трансформаторов и электродвигателей.

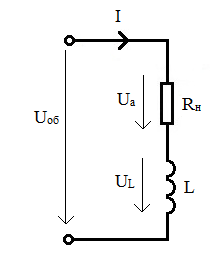
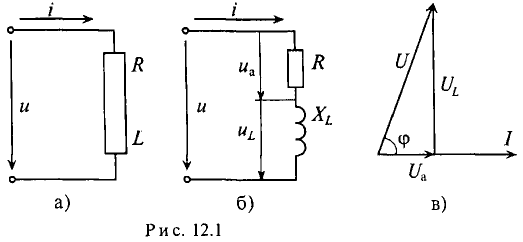
На схеме реальная катушка индуктивности изображается последовательным соединением элементов R и L (рис. 57). На каждом из этих элементов действует напряжение, обозначенное на рис. 57 стрелкой. На сопротивлении действует активное напряжение U_a, а на индуктивности – индуктивное напряжение U_L.

Рис. 57. Последовательное соединение элементов R и L

Известно, что при последовательном соединении элементов цепи общее напряжение равно сумме напряжений на этих элементах.

Сумма эта векторная, арифметически суммировать напряжения в цепях переменного тока нельзя. Складывать векторы можно только по рассмотренным выше правилам сложения векторов.

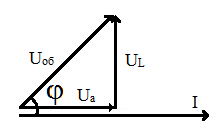
Для понимания работы электрической цепи переменного тока, прежде всего, необходимо построить векторную диаграмму. Для рассматриваемой цепи векторная диаграмма будет иметь вид, показанный на рис. 58.

В последовательных цепях построение диаграмм начинается с вектора тока, так как он одинаков во всех элементах цепи.

Рис. 58. Векторная диаграмма для цепи с последовательным соединением

элементов R и L

Затем проводим вектор напряжения на активном сопротивлении. Он совпадает по фазе с током в цепи.

К концу вектора U_a пристраиваем вектор напряжения U_L на индуктивности. Он направлен вверх, поскольку напряжение на индуктивности опережает ток на 90 градусов. Для построения диаграммы в масштабе смотри раздел Графическое изображение синусоидальных величин.

Общее напряжение, приложенное к цепи является суммой этих двух векторов. Суммируя напряжения U_a и U_L, проведём вектор суммарного напряжения U_об из начала вектора U_a к концу вектора U_L.

Из диаграммы следует, что ток в цепи отстаёт по фазе от приложенного к цепи напряжения U_об на угол φ меньше 90 градусов.

Три напряжения на векторной диаграмме образуют треугольник напряжений. В этом прямоугольном треугольнике гипотенузой является напряжение U_об, а катетами – напряжения U_a и U_L.

По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов.

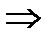
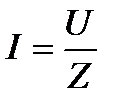
(Здесь и далее, в формулах, стрелка заменяет слово «следовательно») По закону Ома, ток равен напряжению, делённому на сопротивление цепи:

, где

Z– полное сопротивление в цепи, которое учитывает совместное действие активного R и индуктивного X_L сопротивлений.

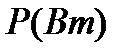
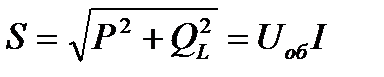
Цепь содержит активный и реактивный компоненты. В резисторе выделяется активная мощность . В катушке выделяется реактивная мощность . Во всей цепи выделяется полная мощность S, измеряемая в вольт-амперах (ВА).

(ВА)

Пример 13.Реальная катушка в цепи синусоидального тока.

В сеть с напряжением 50 В и частотой 50 Гц включена реальная катушка с индуктивностью L = 0,0127 Гн. и активным сопротивлением R = 3 Ом. Определить ток, напряжения на элементах цепи, активную, реактивную и полную мощности катушки.

Реальная катушка индуктивности помимо индуктивности L обладает, также, сопротивлением провода R, которым она намотана. На схеме реальная катушка изображается последовательным соединением сопротивления R и индуктивности L.

Индуктивное сопротивление катушки

X_L=2πfL = 2 ·3,14 ·50 ·0,0127 = 4Ом.

Полное сопротивление цепи

Ток определяется напряжением, приложенным к цепи, и её полным сопротивлением

Напряжения на активном и индуктивном сопротивлениях, входящих в цепь, определим по закону Ома:

напряжение на активном сопротивлении: U_a= I·R== 10 ·3 = 30 В;

напряжение на индуктивном сопротивлении: U_L=I · X_L = 10 ·4 = 40 В.

Активная, реактивная и полная мощности, выделяющиеся в элементах цепи:

Р = U_а ·I = 30 ·10 = 300 Вт;

Q_L = U_L · I= 40·10 = 400 вар:

S = U_об· I = 50 ·10 = 500 BА.

Видео:Переходные процессы | Классический метод расчета переходных процессов. Теория и задачаСкачать

Электрические цепи синусоидального тока

Содержание:

Видео:Урок 4. Расчет цепей постоянного тока. Законы КирхгофаСкачать

Электрические цепи синусоидального тока:

В общем случае цепь переменного тока характеризуется тремя параметрами: активным сопротивлением R, индуктивностью L и емкостью С. В технике часто применяются цепи переменного тока, в которых преобладает один или два из этих параметров.

При анализе работы и расчетах цепей исходят из того, что для мгновенных значений переменного тока можно использовать все правила и законы постоянного тока.

Видео:Катушка индуктивности в цепи переменного токаСкачать

Цепь с активным сопротивлением

Активным сопротивлением R обладают элементы, которые нагреваются при прохождении через них тока (проводники, лампы накаливания, нагревательные приборы и т.д.).

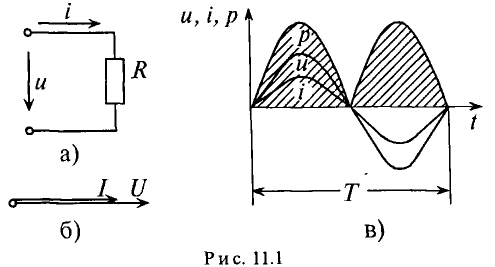
Если к активному сопротивлению R (рис. 11.1) приложено синусоидальное напряжение

где

Ток в цепи с активным сопротивлением совпадает по фазе с напряжением, так как начальные фазы их равны ( 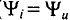= 0). Векторная диаграмма для цепи с активным сопротивлением изображена на рис. 11.16, временная диаграмма изображена на рис. 11.1в.

Математическое выражение закона Ома для цепи переменного тока с активным сопротивлением имеет вид:

Это вытекает из выражения (11.1), если левую и правую части уравнения разделить на 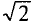=1,41.

Таким образом, действующее значение синусоидального тока I пропорционально действующему значению синусоидального напряжения U и обратно пропорционально сопротивлению R участка цепи, к которому приложено напряжение U. Такая интерпретация закона Ома справедлива как для мгновенных, так и для действующих и амплитудных значений синусоидального тока.

Активная мощность

Мгновенная мощность в цепи с активным сопротивлением определяется произведением мгновенных значений напряжения ка, т. е. р = ui. Это действие производится над кривыми тока и ряжения в определенном масштабе (рис. 11.1в). В результате учена временная диаграмма мгновенной мощности р. Как видно из временной диаграммы, мощность в цепи с активным сопротивлением изменяется по величине, но не изменяется по направлению (рис. 11.1в). Эта мощность (энергия) необратима. От источника она поступает на потребитель и полностью преобразуется в другие виды мощности (энергии), т.е. потребляется. Такая потребляемая мощность называется активной.

Поэтому и сопротивление R, на котором происходит подобное образование, называется активным сопротивлением, цепи с активным сопротивлением мгновенная мощность характеризует скорость преобразования электрической энергии в другие виды энергии.

Количественно мощность в цепи с активным сопротивлением определяется следующим образом:

Мгновенная мощность в цепи синусоидального тока с активным сопротивлением представляет собой сумму двух величин -постоянной мощности UI и переменной 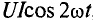, изменяющейся с двойной частотой.

Средняя за период мощность, равная постоянной составляющей мгновенной мощности UI, является активной мощностью Р. Среднее за период значение переменной составляющей, как и всякой синусоидальной величины, равно нулю, то есть

Таким образом, величина активной мощности в цепи синусоидального тока с активным сопротивлением с учетом закона Ома определяется выражением:

где U- действующее значение напряжения; I— действующее значение тока.

Единицей активной мощности является ватт:

Поверхностный эффект и эффект близости

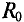
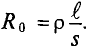
Сопротивление проводника постоянному току называют омическим сопротивлением и определяют выражением (2.8) Сопротивление проводника переменному току R называют активным.

Оказывается, что сопротивление проводника переменному току больше его омического сопротивления за счет так называемого поверхностного эффекта и эффекта близости, т. е.

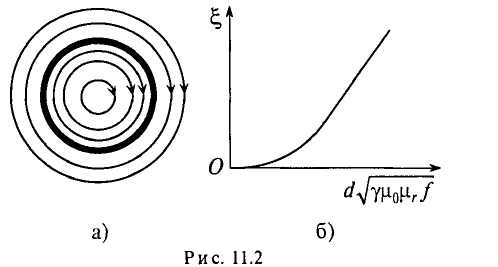
Увеличение активного сопротивления вызвано неодинаковой плотностью тока в различных сечениях проводника (рис. 11.2а).

На рис. 11.2а изображено магнитное поле проводника цилиндрического сечения. Если по проводнику проходит переменный ток, то он создает переменный магнитный поток внутри и вне проводника. Этот поток в различных сечениях проводника индуктирует ЭДС самоиндукции, которая, согласно правилу Ленца. противодействует изменению тока как причине создания ЭДС Очевидно, центр проводника охвачен большим количеством магнитных линий (большее потокосцепление), чем слои, близкие к поверхности. Следовательно, в центре проводника ЭДС (сопротивление) больше, чем на поверхности проводника. Плотность на поверхности больше, чем в центре. Поэтому это явление и называется поверхностным эффектом.

Таким образом, поверхностный эффект уменьшает сечение проводника для переменного тока, а следовательно, увеличивает активное сопротивление R.

Отношение активного сопротивления проводника к его сопротивлению определяет коэффициент поверхностного эффекта 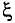(кси)

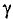
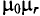
График зависимости коэффициента поверхностного эффекта от параметра проводника d, его удельной проводимости , магнитной проницаемости материала проводника и частоты переменного тока , проходящего по проводнику, показан на рис. 11.26.

При токах большой частоты (радиочастотах) ток в центре проводника отсутствует. Поэтому такие проводники делают трубчатыми, т.е. полыми.

На величину активного сопротивления проводника R оказывает влияние и эффект близости.

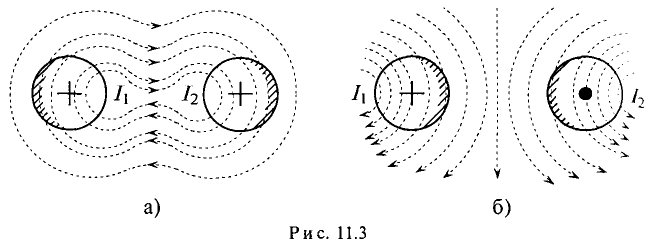
Если токи в двух параллельных проводах, расположенных близко друг к другу, направлены в одну сторону, то элементы сечения водников, удаленных на большее расстояние друг от друга, цепляются с меньшим магнитным потоком и имеют большую плотность тока (заштриховано на рис. 11.3а), чем элементы сечения проводников, расположенные близко друг к другу.

Если же токи в близко расположенных параллельных проводах направлены в различные стороны, то большая плотность тока на-дается в элементах сечения проводников, расположенных ближе друг к другу (заштриховано на рис. 11.36).

Таким образом, эффект близости в проводниках также влияет активное сопротивление проводников за счет наведения в различных элементах сечений проводников различных ЭДС взаимоиндукции, направление которых определяется правилом Ленца.

Видео:Резонанс напряжений в электрической цепиСкачать

Цепь с идеальной индуктивностью

Идеальной называют индуктивность L такой катушки, активным сопротивлением R и емкостью С которой можно пренебречь, т.е. R= О и С=0.

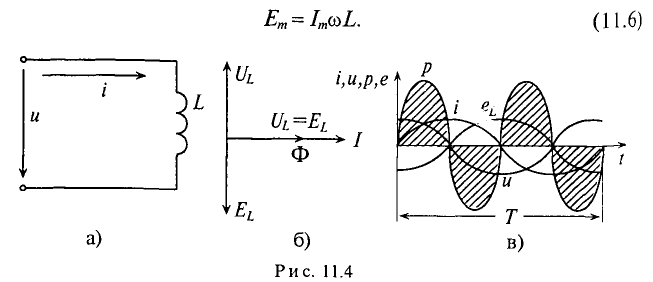
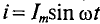
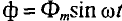
Если в цепи идеальной катушки индуктивностью L (рис. 11.4а) проходит синусоидальный ток , то этот ток создает в катушке синусоидальный магнитный поток , который индуктирует в катушке ЭДС самоиндукции, равную согласно (9.11)

так как

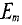
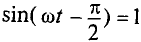
Очевидно, эта ЭДС достигает своего амплитудного значения тогда, когда :

Тогда

Таким образом, ЭДС самоиндукции в цепи с идеальной индуктивностью L, как и ток, вызвавший эту ЭДС, изменяется по синусоидальному закону, но отстает от тока по фазе на угол 90° = 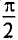(рис. 11.46, в).

По второму закону Кирхгофа для мгновенных значений можно записать

Откуда

Тогда напряжение, приложенное к цепи с идеальной индуктивностью (см. (11.5)):

Очевидно, напряжение достигает своего амплитудного значения U_m тогда, когда :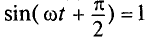

Следовательно,

Таким образом, напряжение, приложенное к цепи с идеальной ин-ивностью, как и ток в этой цепи, изменяется по синусоидально-жону, но опережает ток по фазе на угол 90°= 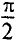(рис. 11.46, в).

Резюмируя все вышесказанное, можно сделать вывод: для существования тока в цепи с идеальной индуктивностью необходимо ожить к цепи напряжение, которое в любой момент времени но по величине, но находится в противофазе с ЭДС, вызванной таким током (рис. 11.46, в).

Временная диаграмма (рис. 11.4в) еще раз иллюстрирует правило Ленца: ЭДС 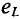противодействует изменению тока.

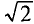
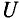
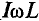
Если уравнение (11.10) разделить на =1,41, то получается =, откуда

Это уравнение (11.12а) и есть математическое выражение закона Ома для цепи синусоидального тока с идеальной индуктивностью. Очевидно, знаменатель этого уравнения есть не что иное, как сопротивление, которое называют индуктивным сопротивлением X_L.

Закон Ома для этой цепи можно записать иначе:

Индуктивное сопротивление X_L — это противодействие, которое ЭДС самоиндукции e_L оказывает изменению тока.

Реактивная мощность в цепи с индуктивностью

Мгновенная мощность для цепи синусоидального тока с идеальной катушкой равна произведению мгновенных значений напряжения и тока

где

Следовательно,

Полученное уравнение умножают и делят на 2:

Таким образом, мощность в цепи синусоидального тока с идеальной катушкой индуктивности изменяется по синусоидальному закону с двойной частотой.

Следовательно, среднее значение этой мощности за период Яс, как и любой синусоидальной величины, т. е. активная потребляемая мощность, в этой цепи равна нулю, Р= 0.

Временная диаграмма (рис. 11,4в) подтверждает этот вывод. На диаграмме видно, что мгновенная мощность (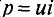) в рассматриваемой цепи изменяется по синусоидальному закону с двойной частотой.

То есть в 1-ю и 3-ю четверти периода мощность (энергия) источника накапливается в магнитном поле индуктивности. Максимальное значение накапливаемой в магнитном поле идеальной катушки энергии по (9.12) равно

Во 2-ю и 4-ю четверти периода эта мощность (энергия) из магнитного поля идеальной катушки возвращается к источнику.

Таким образом, в цепи переменного тока с идеальной катушки мощность не потребляется (Р= 0), а колеблется между источником и магнитным полем индуктивности, загружая источник и провода.

Такая колеблющаяся мощность (энергия), в отличие от активной, потребляемой, называется реактивной.

Обозначается реактивная мощность буквой Q и измеряется в варах, т.е. [Q]=вар (вольт-ампер реактивный).

Величина реактивной мощности в рассматриваемой цепи определяется выражением

Так как реактивная мощность Q_L имеет место в цепи с индуктивным сопротивлением, то индуктивное сопротивление считается реактивным сопротивлением X индуктивного характера, т. е. X_L.

Видео:Активное и реактивное сопротивление в цепи переменного тока. 11 класс.Скачать

Цепь с емкостью

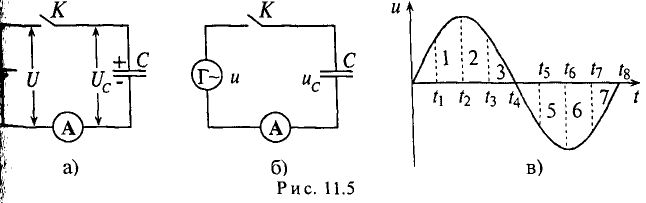
Если конденсатор емкостью С подключить к источнику с постоянным напряжением U (рис. 11.5а), то ток зарядки конденсатора ходит в цепи очень короткое время, пока напряжение на конденсаторе U_c не станет равным напряжению источника U.

Ток в рассматриваемой цепи (рис. 11.5а) практически отсутствует (амперметр А покажет I=0).

Если же конденсатор подключить к источнику с синусоидальным напряжением (рис. 11.56), то ток в цепи конденсатора существует все время, пока цепь замкнута, и амперметр А покажет этот ток. Ток в цепи конденсатора, подключенного к источнику с синусоидальным напряжением, имеет место потому, что напряжена конденсаторе U_c отстает по фазе от напряжения источника и зарядке, и при разрядке конденсатора. Например, пока напряжение на конденсаторе достигает значения 1, напряжение источника достигнет значения 2 (рис. 11.5в), т. е. конденсатор заряжается; пока конденсатор зарядится до напряжения 2, напряжение источника уменьшится до напряжения 3 — конденсатор разряжается на источник и т.д. Однако ток проходит только в цепи конденсатора. Через диэлектрик конденсатора ток не проходит.

Таким образом, если к конденсатору емкостью С приложено синусоидальное напряжение 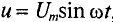, то в цепи конденсатора проходит ток i (рис. 11.6а):

где q= Си согласно (6.3).

Очевидно, ток в цепи конденсатора достигает амплитудного значения тогда, когда :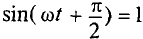

Тогда

Как видно, ток в цепи конденсатора, как и напряжение, приложенное к его обкладкам, изменяется по синусоидальному закону, однако опережает это напряжение по фазе на угол 90°=

Следовательно, напряжение отстает по фазе от тока на 90° = (рис. 11.66).

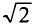
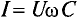
Если уравнение (11.17) разделить на = 1,41, то получится равенство или

Это равенство (11.19а) и является математическим выражением закона Ома для цепи переменного тока с емкостью.

Очевидно, знаменатель этого равенства является сопротивлением конденсатора Х_с, которое называется емкостным сопротивлением:

Когда закон Ома для цепи с конденсатором можно записать:

Емкостное сопротивление — это противодействие, которое оказывает напряжение заряженного конденсатора напряжению, приложенному к нему (рис. 11,5а).

Реактивная мощность в цепи с конденсатором

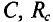
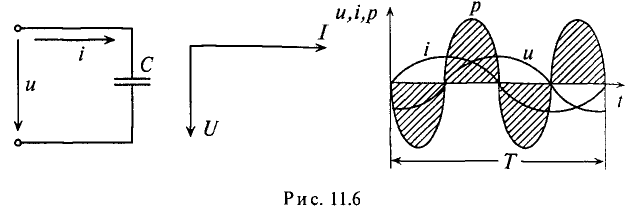
Если в цепи конденсатора емкостью = 0 (рис. 11.6а) проходит ток i, изменяющийся по синусоидальному закону:

Напряжение и, приложенное к этому конденсатору (рис. 11.6), будет равно

Мгновенная мощность в цепи с конденсатором

Мощность в цепи с конденсатором, подключенным к источнику с синусоидальным напряжением, изменяется по синусоидальному закону с двойной частотой (рис. 11.6в).

Следовательно, активная мощность Р в рассматриваемой цепи 1С. 11.6а), равная среднему значению мгновенной мощности за период, имеет нулевое значение, Р= 0.

Это следует и из временной диаграммы (рис. 11.6в). На временной диаграмме видно, что изменение мгновенной мощности р по синусоидальному закону происходит с двойной частотой: 2-ю и 4-ю четверти периода мощность (энергия) источника накапливается в электрическом поле конденсатора.

Максимальное значение энергии, накапливаемой в электрическом поле конденсатора, равно

В 1-ю и 3-ю четверти периода эта мощность (энергия) из электрического поля конденсатора возвращается к источнику.

Таким образом, в цепи переменного тока с конденсатором происходит колебание мощности (энергии) между источником и электрическим полем конденсатора. Такая колеблющаяся, но не потребляемая мощность называется реактивной мощностью.

Величина реактивной мощности в цепи конденсатора определяется выражением

Из временных диаграмм (рис. 11.4в, 11.6в) видно, что реактивная мощность в цепи конденсатора изменяется в противофазе с реактивной мощностью в цепи с идеальной катушкой. Отсюда и знак «минус» в уравнении (11.21) — аналитическом выражении мгновенной мощности в цепи с конденсатором.

Так как реактивная мощность Qc имеет место в цепи с емкостным сопротивлением, то это емкостное сопротивление считается реактивным сопротивлением Х емкостного характера (Х_с).

Видео:Почему UL опережает iL на 90°│Сдвиг фаз между UL и iL│Катушка в цепи переменного токаСкачать

Расчет линейных электрических цепей синусоидального тока

Расчет электрических цепей синусоидального тока производится преимущественно с помощью векторных диаграмм. В нашей главе рассматривается расчет неразветвленных цепей синусоидального тока, содержащих активное сопротивление R, активность L и емкость С в различных сочетаниях.

Цепь с активным сопротивлением и индуктивностью

Если по цепи с реальной катушкой, обладающей активным сопротивлением R и индуктивностью L, проходит синусоидальный ток 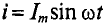(рис. 12.1а), то этот ток создает падение напряжения на активном сопротивлении проводников катушки и индуктивном сопротивлении катушки

Следовательно, по второму закону Кирхгофа, для мгновенных значений, приложенное к реальной катушке напряжение можно записать

Это равенство справедливо для неразветвленной цепи синусоидального тока с последовательно включенными активным сопротивлением R и индуктивным сопротивлением X_L (рис. 12.16).

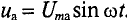
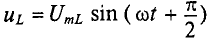
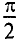
Активное напряжение (рис. 11.16) совпадет по фазе с током и может быть записано . Индуктивное напряжение опережает ток на угол 90° = .

Мгновенное значение напряжения, приложенного к цепи, определяется алгебраической суммой мгновенных значений напряжений 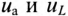согласно (12.1). А действующее значение этого напряжения U определяется геометрической суммой их действующих значений

Это равенство лежит в основе построения векторной диаграммы (рис. 12.1 в).

Из векторной диаграммы (рис. 12.1 в) видно, что напряжение U, приложенное к реальной катушке, опережает по фазе ток 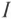на угол ф. Мгновенное значение этого напряжения может быть записано:

где ф — это международное обозначение угла сдвига фаз между током и напряжением для любой цепи переменного тока.

Воспользовавшись теоремой Пифагора для определения гипотенузы прямоугольного треугольника, по векторной диаграмме (рис. 12.1 в) определяется напряжение

Равенство (12.4) является математическим выражением закона Ома для цепи синусоидального тока с активным R и индуктивным XL сопротивлениями в неразветвленной цепи.

Знаменатель этого равенства является сопротивлением этой цепи, которое называется полным, или кажущимся, сопротивлением цепи синусоидального тока. Обозначается кажущееся (полное) сопротивление любой цепи переменного тока буквой Z:

где Z_k — полное, или кажущееся, сопротивление реальной катушки.

Тогда закон Ома для любой цепи переменного тока в общем виде можно записать

где Z — кажущееся сопротивление этой цепи.

Треугольники напряжений, сопротивлений, мощностей

Треугольник, все стороны которого изображены векторами напряжений, называется треугольником напряжений. Пользуясь векторной диаграммой для неразветвленной цепи с активным и индуктивным сопротивлениями (рис. 12.1в), выделяем треугольник напряжений (рис. 12.2а).

Связь между напряжениями в данной цепи можно рассматривать как соотношение между сторонами и углами прямоугольного треугольника:

Если все стороны треугольника напряжений разделить на ве-1ину тока в цепи, то получится подобный прямоугольный треугольник, все стороны которого в определенном масштабе изображают сопротивления цепи, т. е. получится треугольник составлений (рис. 12.16). Сопротивления не являются векторными величинами. Из треугольника сопротивлений можно определить:

Обычно тригометрические функции угла ф определяются из треугольника сопротивлений отношением (12.9).

Если все стороны треугольника напряжений умножить на величину тока цепи, то получится подобный прямоугольный треугольник, все стороны которого в определенном масштабе изображают мощности цепи, т.е. получится треугольник мощностей (рис. 12.2в).

Произведение напряжения и тока цепи характеризует полную мощность цепи

которая измеряется в вольт-амперах, т.е.

Однако потребляется в цепи только часть полной мощности — активная мощность

где cos ф показывает, какая часть полной мощности 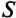потребляется в цепи, поэтому cos ф называют коэффициентом мощности:

Полная мощность цепи S называется кажущейся. Из того же треугольника мощностей (рис. 12.2в) записать:

Построив треугольники напряжений, сопротивлений и мощностей для любой цепи синусоидального тока, по выражениям (12.7)—(12.14) можно рассчитать параметры этой цепи.

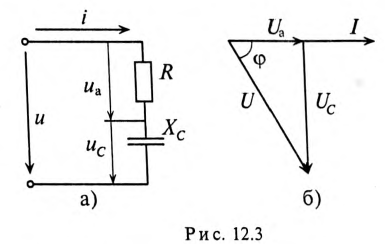
Цепь с активным сопротивлением и емкостью

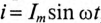
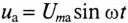
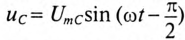
Если в цепи с последовательно включенными активным сопротивлением R и емкостью С протекает синусоидальный ток , то он создает падение напряжения на активном сопротивлении и на емкостном сопротивлении . Векторная диаграмма для этой цепи изображена на рис. 12.36.

Напряжение цепи изменяется, как и ток, по синусоидальному закону и отстает по фазе от тока на угол ф

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Лекция 116. Энергия катушки индуктивностиСкачать

Лекция №20. Переменный электрический ток

2. Действующее значение переменного тока

3. Электрическая цепь с резистором

4. Электрическая цепь с катушкой индуктивности

5. Электрическая цепь с конденсатором

6. Закон Ома для цепи переменного тока

8. Резонанс в электрических цепях. Резонанс напряжений

Переменный электрический ток

Установившиеся вынужденные электромагнитные колебания в цепи с резистором, катушкой индуктивности и конденсатором можно рассматривать как переменный электрический ток. Если подводимые к контуру внешняя ЭДС или напряжение периодически изменяются по гармоническому закону, то переменный ток называют синусоидальным (рис. 20.1):

где – мгновенное значение силы тока, то есть значение тока для каждого момента времени; – амплитудное значение силы тока.

При частоте (промышленная частота) период электромагнитных колебаний составляет .

Ввиду того, что в течение периода сила переменного тока изменяется, о величине такого тока судят не по мгновенным значениям, а по действующему или эффективному значению . При этом действие переменного тока оценивают по тепловому эффекту, который сравнивают с тепловым эффектом постоянного тока.

Действующее значение переменного тока

Действующим (эффективным) значением переменного тока называют такую величину, которая равна силе постоянного тока, выделяющего в проводнике такое же количество теплоты, что и данный переменный ток за одно и то же время. Действующее значение переменного синусоидального тока связано с его амплитудным значением соотношением

(20.1)

Для мгновенных значений синусоидальных токов выполняются закон Ома и правила Кирхгофа.

Рассмотрим цепи, содержащие резистор, катушку индуктивности, конденсатор и все три элемента, соединенные последовательно, на зажимах которых приложено переменное напряжение

где – амплитудное значение напряжения.

Электрическая цепь с резистором

Сила тока, протекающего через резистор (рис. 20.2), определяется законом Ома

(20.2)

где – амплитуда силы тока. Очевидно, что при чисто активном (R) характере цепи сдвиг фаз колебаний тока и напряжения равен нулю (рис.

Электрическая цепь с катушкой индуктивности

В катушке без потерь () будет протекать ток, если напряжение на ее выводах компенсирует ЭДС самоиндукции (рис. 20.4), то есть

(20.3)

(20.4)

Постоянная интегрирования А=0, так как ток изменяется по гармоническому закону, то есть не имеет постоянной составляющей. Очевидно, что амплитуда тока в цепи с катушкой

(20.5)

где – индуктивное сопротивление, зависящее от частоты. При (при протекании постоянного тока) .

Таким образом, в цепи с катушкой индуктивности колебания силы тока отстают по фазе на от колебаний напряжения (рис. 20.5).

Электрическая цепь с конденсатором

Если пренебречь активным сопротивлением соединительных проводов и обкладок конденсатора (рис. 20.6), то напряжение на конденсаторе будет равно напряжению на зажимах цепи, то есть

откуда заряд конденсатора

Сила тока в цепи конденсатора

(20.6)

где , — емкостное сопротивление цепи. Чем меньше частота , тем больше . Поэтому в цепи постоянного тока () и конденсатор не проводит электрический ток.

Таким образом, в цепи с конденсатором колебания силы тока опережают по фазе на колебания напряжения (рис. 20.7).

Закон Ома для цепи переменного тока

Рассмотрим теперь электрическую цепь из последовательно соединенных резистора, катушки индуктивности и конденсатора (рис. 20.8).

По второму правилу Кирхгофа для мгновенных значений напряжение на зажимах цепи равно сумме напряжений на отдельных элементах

Построим векторную диаграмму цепи с учетом полученных ранее фазовых соотношений: а) напряжение на резисторе совпадает по фазе с током; б) напряжение на катушке индуктивности опережает по фазе ток на ; в) напряжение на конденсаторе отстает по фазе от тока на (рис. 20.9).

Из векторной диаграммы найдем модуль действующего значения напряжения

(20.9)

где – реактивная составляющая напряжения.

Учитывая, что , , , получим:

где Z – полное сопротивление цепи. Выражение

(20.10)

называется законом Ома для цепи переменного тока.

Разность называют реактивным сопротивлением. Из векторной диаграммы следует, что угол сдвига фаз между током и напряжением для рассматриваемой схемы

(20.11)

Если , цепь имеет индуктивный характер, ; если , цепь имеет емкостный характер, ; если , то реактивное сопротивление цепи , и цепь имеет активный характер даже при наличии в ней L и C.

Мгновенная мощность, развиваемая в цепи переменного тока, равна произведению мгновенных значений силы тока и напряжения:

(

Среднее за период значение мгновенной мощности называют активной мощностью

(20.13)

Из-за наличия сдвига фаз знаки у тока и напряжения в данный момент времени могут быть разные. Поэтому мгновенная мощность может быть отрицательной в некоторые доли периода переменного тока, что означает возвращение энергии из цепи источнику тока.

На рис.20.10 приведены графики изменения мгновенной мощности при различных углах сдвига фаз между колебаниями напряжения и тока.

При в любой момент времени мощность положительна, она расходуется в цепи на совершение различных видов работы. При в отдельные промежутки времени мощность отрицательна. Это объясняется тем, что при наличии в цепи катушки индуктивности возрастание тока приводит к созданию в ней магнитного поля, которое обладает запасом энергии. При уменьшении силы тока магнитное поле исчезает и запасенная в нем энергия возвращается к источнику тока (генератору). Аналогичный процесс происходит при наличии в цепи конденсатора: в течение той четверти периода, когда происходит зарядка конденсатора, энергия в нем запасается, а когда конденсатор разряжается, он отдает в цепь запасенную энергию.

При положительная мощность равна отрицательной мощности, работа тока за период равна нулю, следовательно, средняя мощность также равна нулю. При этом периодически энергия запасается в магнитном и электрическом полях, а затем снова передается генератору. Последний случай возможен лишь при R=0.

Подставив (20.12) в (20.13) и выполнив преобразования, найдем среднее значение мощности переменного тока:

, (20.14)

где – косинус угла сдвига фаз, который называется коэффициентом мощности.

Формула (20.14) показывает, что развиваемая в цепи переменного тока мощность зависит не только от силы тока и напряжения, но и от сдвига фаз между напряжением и током.

Коэффициент мощности характеризует потери энергии в цепи и, следовательно, является важнейшей технико-экономической характеристикой при проектировании электрооборудования переменного тока. Если нагрузки в цепи имеют большие емкостные и индуктивные сопротивления, то и может быть много меньше единицы. В этих случаях для передачи требуемой активной мощности Р (при заданном напряжении) необходимо увеличивать силу тока, что приводит к выделению в цепи большого количества теплоты. Поэтому приходится либо увеличивать сечение проводов (R

1/S), либо распределять реактивные нагрузки так, чтобы был по возможности ближе к единице.

Резонанс в электрических цепях. Резонанс напряжений

Резонансом в электрической цепи называется режим участка, содержащего индуктивный и емкостный элементы, при котором угол сдвига фаз колебаний напряжения и тока равен нулю. Резонанс характеризуется рядом особенностей, которые обусловили его широкое применение в радиотехнике, электротехнике, измерительной технике и других областях.

Различают несколько видов резонанса: резонанс напряжений (при последовательном соединении элементов), резонанс токов (при параллельном соединении элементов), резонанс в магнитно-связанных цепях и др.

Резонанс напряжений. Из выражения (1) следует, что при последовательном соединении ток в цепи приобретает максимальное значение при , то есть при Этому условию удовлетворяет частота

(20.15)

В этом случае , , падения напряжения на катушке индуктивности и конденсаторе одинаковы по величине и противоположны по фазе (рис. 20.11). Таким образом, при резонансе напряжений

,

(20.16)

где Q – добротность контура. Так как добротность колебательных контуров больше единицы, то напряжение, как на катушке индуктивности, так и на конденсаторе превышает напряжение U, приложен-ное к цепи. Из выражения (20.16) следует, что доброт-ность контура показывает, во сколько раз при резонансе напряжение на реактивных элементах больше по величине входного напряжения.

Явление резонанса напряжений используется в радиотехнике и электронике для усиления колебаний напряжения какой-либо определенной частоты. В электроэнергетике явление резонанса напряжений необходимо учитывать при выборе изоляции высоковольтного оборудования, так как иначе может произойти ее пробой.

📸 Видео

Урок 358. Активное сопротивление в цепи переменного тока. Действующее значение тока и напряженияСкачать

Лекция по электротехнике 1.3 - Пассивные элементы в электрической цепиСкачать

Основы электротехники. 02. Электрическая цепьСкачать

Что такое РЕЗОНАНС НАПРЯЖЕНИЙ | САМОЕ ПОНЯТНОЕ объяснениеСкачать

Урок №2. Основные элементы электрической цепи (часть 1)Скачать

Последовательное соединение RLC элементов в цепи синусоидального токаСкачать

2 2 Элементы схем замещенияСкачать

Индуктивность Дифференцирующая цепочка или Шунтирование нагрузки электрической цепиСкачать

АКТИВНОЕ И РЕАКТИВНОЕ СОПРОТИВЛЕНИЕ | ОБЪЯСНЯЮ НА ПАЛЬЦАХСкачать

3 9 Индуктивно связанные катушки в цепи переменного синусоидального токаСкачать

Всё про самоиндукцию за 3 часа. Катушка индуктивности в электрических цепях | ЕГЭ 2024 по физикеСкачать