Уравнение движения в цилиндрических координатах

Если материальная точка P движется по кривой траектории, то положение точки может быть определено тремя цилиндрическими координатами: r, θ, z. Тогда положение точки, её скорость и ускорение могут быть записаны в единицах цилиндрических координат следующим образом:

Если разложить силу, действующую на материальную точку, вдоль единичных векторов цилиндрической системы координат, то уравнение движения можно записать в виде:

Для выполнения равенства, соответствующие компоненты u_r,u_θ,u_z левой части уравнения должны быть равны соответствующим компонентам в правой части уравнения. Таким образом, уравнение движения можно записать с помощью следующих скалярных компонентов:

Если движение происходит в двумерных координатах r-θ, то для описания движения необходимы только два первых уравнения.

Центростремительное и нормальное ускорение

Обычно задача заключается в определении компонентов результирующей силы: F_θ,F_r, F_z , которые приводят частицу в движение и задают ей определённое ускорение.

Сила P создаёт движение по траектории r = f(θ). Нормальная сила N всегда перпендикулярна касательной траектории в данной точке, в то время, как сила трения F всегда направлена вдоль касательной и против направления движения. Направления сил N и F могут быть определены относительно r-координаты используя угол θ, который определён между прямой-направлением радиуса и касательной в заданной точке.

Угол θ определяется смещением точки на расстояние ds вдоль траектории, радиальное перемещение составляет dr и перемещение в направлении касательной r dθ. Так как эти две составляющиевзаимно перпендикулярны, угол θ может быть определён из равенства:

Если угол θ положителен, то он измеряется от радиальной линии против направления хода часов или в положительном направлении угла θ. Если угол отрицательный, то он измеряется в обратном направлении (по часовой стрелке).

Например, кардиоида, описанная уравнением

когда θ=30°, tg = a(1+ cos 30°)/(-a sen 30°) = -3.73 2 , или θ = -75°, измеренный против направления хода часов, как представлено на изображении.

Алгоритм решения задач

Цилиндрические координаты удобно использовать для анализа систем, в которых траектории движения заданы относительно радиальной линии, или могут быть удобным образом выражены в цилиндрических координатах. Определив координаты точки, уравнения движения могут быть применены для выражения силы в виде компонентов ускорения.

1. Установить инерциальную систему координат r, θ, z и изобразить диаграмму свободного тела
2. Положить ускорения a_r, a_θ, a_z направлены вдоль положительного направления осей r, θ, z, если направления неизвестны
3. Определить все неизвестные величины в задачи

Применить уравнения движения

Видео:Скорость и ускорение точки в полярных координатахСкачать

Цилиндрические координаты: система, изменение и упражнения

Цилиндрические координаты: система, изменение и упражнения — Наука

Видео:Цилиндрическая система координат(ЦСК).Тройной интегралСкачать

Содержание:

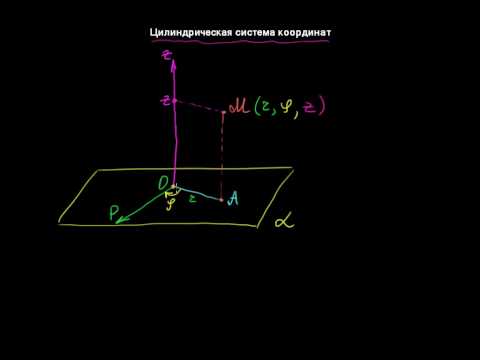
В цилиндрические координаты Они используются для определения местоположения точек в трехмерном пространстве и состоят из радиальной координаты ρ, азимутальной координаты φ и координаты высоты. z.

Точка п расположенная в пространстве проецируется ортогонально на плоскость XY приводя к сути П ‘ в этом самолете. Расстояние от начала координат до точки П ‘ определяет координату ρ, а угол, образованный осью Икс с лучом OP ‘ определяет координату φ. Наконец, координата z ортогональная проекция точки п на оси Z. (см. рисунок 1).

Радиальная координата ρ всегда положительна, азимутальная координата φ изменяется от нуля радиан до двух пи радиан, а координата z может принимать любое действительное значение:

Видео:Уравнение координат при равноускоренном движенииСкачать

База вектора в цилиндрических координатах

База цилиндрических единичных векторов определяется Uρ, Uφ, Уз.

Вектор Uρ касается прямой φ = ctte и z = ctte (направленной радиально наружу), вектор Uφ касается прямой ρ = ctte, z = ctte и, наконец, Уз имеет то же направление оси Z.

В основании цилиндрического блока вектор положения р точки P записывается векторно так:

р = ρ Uρ + 0 Uφ + z Уз

С другой стороны, бесконечно малое смещение dр из точки P это выражается следующим образом:

dр = dρ Uρ + ρ dφ Uφ + дз Уз

Точно так же бесконечно малый элемент объема dV в цилиндрических координатах равен:

Видео:Уравнение движенияСкачать

Примеры

Существует бесчисленное множество примеров использования и применения цилиндрических координат. В картографии, например, цилиндрическая проекция, исходя именно из этих координат. Еще примеры:

Видео:Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

Пример 1

Цилиндрические координаты находят применение в технике. В качестве примера у нас есть система размещения данных на жестком диске CHS (Cylinder-Head-Sector), которая фактически состоит из нескольких дисков:

— Цилиндр или дорожка соответствует координате ρ.

— Сектор соответствует положению φ диска, вращающегося на высокой угловая скорость.

— Головка соответствует положению z считывающей головки на соответствующем диске.

Каждый байт информации имеет точный адрес в цилиндрических координатах (C, S, H).

Видео:Траектория и уравнения движения точки. Задача 1Скачать

Пример 2

Строительные краны фиксируют положение груза в цилиндрических координатах. Горизонтальное положение определяется расстоянием до оси или стрелкой крана ρ и его угловым положением φ относительно некоторой исходной оси. Вертикальное положение груза определяется координатой z высоты.

Видео:Физика - уравнения равноускоренного движенияСкачать

Решенные упражнения

Видео:Полярная система координатСкачать

Упражнение 1

Есть точки P1 с цилиндрическими координатами (3, 120º, -4) и точка P2 с цилиндрическими координатами (2, 90º, 5). Найди Евклидово расстояние между этими двумя точками.

Решение: Прежде всего, мы переходим к нахождению декартовых координат каждой точки по формуле, приведенной выше.

P1 = (3 * cos 120º, 3 * sin 120º, -4) = (-1,5, 2,60, -4)

P2 = (2 * cos 90º, 2 * sin 90º, 5) = (0, 2, 5)

Евклидово расстояние между точками P1 и P2 равно:

d (P1, P2) = √ ((0 — (-1,5)) 2 +(2 – 2.60) 2 +(5 -(-4)) 2 ) =…

Видео:§55 Цилиндрическая система координатСкачать

Упражнение 2.

Точка P имеет декартовы координаты (-3, 4, 2). Найдите соответствующие цилиндрические координаты.

Решение: Переходим к нахождению цилиндрических координат, используя приведенные выше соотношения:

ρ = √ (x 2 + и 2 ) = √((-3) 2 + 4 2 ) = √(9 + 16) = √(25) = 5

φ = arctan (y / x) = arctan (4 / (- 3)) = -53,13º + 180º = 126,87º

Следует помнить, что функция арктангенса является многозначной с периодичностью 180º. Кроме того, угол φ должен принадлежать второму квадранту, поскольку координаты x и y точки P находятся в этом квадранте. Это причина, по которой к результату φ было добавлено 180 °.

Видео:Пример решения тройного интеграла в цилиндрических координатах - bezbotvyСкачать

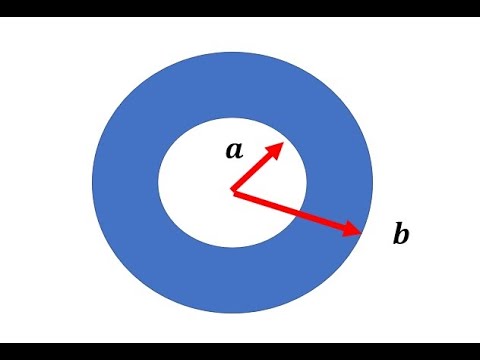
Упражнение 3.

Выразите в цилиндрических координатах и ​​декартовых координатах поверхность цилиндра радиуса 2, ось которого совпадает с осью Z.

Решение: Подразумевается, что цилиндр имеет бесконечную протяженность в направлении z, поэтому уравнение указанной поверхности в цилиндрических координатах имеет вид:

Чтобы получить декартово уравнение цилиндрической поверхности, берется квадрат обоих членов предыдущего уравнения:

Умножаем на 1 оба члена предыдущего равенства и применяем фундаментальное тригонометрическое тождество (сен 2 (φ) + cos 2 (φ) =1 ):

(сен 2 (φ) + cos 2 (φ) ) * ρ 2 = 1 * 4

Скобка предназначена для получения:

(ρ sin (φ)) 2 + (ρ cos (φ)) 2 = 4

Мы помним, что первые круглые скобки (ρ sin (φ)) — это координата y точки в полярных координатах, а круглые скобки (ρ cos (φ)) представляют координату x, поэтому мы имеем уравнение цилиндра в декартовых координатах:

Вышеупомянутое уравнение не следует путать с уравнением окружности в плоскости XY, так как в этом случае оно будет выглядеть так: .

Видео:§30 Уравнения кривых второго порядка в полярных координатахСкачать

Упражнение 4.

Цилиндр с радиусом R = 1 м и высотой H = 1 м имеет свою массу, распределенную радиально в соответствии со следующим уравнением: D (ρ) = C (1 — ρ / R), где C — постоянная величина C = 1 кг / м. 3 . Найдите общую массу цилиндра в килограммах.

Решение: Во-первых, необходимо понять, что функция D (ρ) представляет объемную массовую плотность и что массовая плотность распределена в цилиндрических оболочках с уменьшающейся плотностью от центра к периферии. Бесконечно малый элемент объема в соответствии с симметрией задачи:

Следовательно, бесконечно малая масса цилиндрической оболочки будет:

Следовательно, общая масса цилиндра будет выражаться следующим образом: определенный интеграл:

M = ∫_или р D (ρ) dV = ∫_или р C (1 — ρ / R) ρ dρ 2π H = 2π H C ∫_или р (1 — ρ / R) ρ dρ

Решение указанного интеграла получить нетрудно, его результат:

∫_или р (1 — ρ / R) ρ dρ = (⅙) R 2

Включая этот результат в выражение массы цилиндра, получаем:

M = 2π H C (⅙) R 2 = ⅓ π H C R 2 =

⅓ π 1м * 1кг / м 3 * 1 м 2 = π / 3 кг ≈ 1,05 кг

Видео:Уравнение движения с постоянным ускорением | Физика 10 класс #6 | ИнфоурокСкачать

Ссылки

1. Арфкен Г. и Вебер Х. (2012). Математические методы для физиков. Подробное руководство. 7-е издание. Академическая пресса. ISBN 978-0-12-384654-9
2. Расчет cc. Решенные задачи цилиндрических и сферических координат. Получено с: calculo.cc
3. Вайсштейн, Эрик В. «Цилиндрические координаты». Материал из MathWorld — сеть Wolfram Web. Получено с: mathworld.wolfram.com
4. википедия. Цилиндрическая система координат. Получено с: en.wikipedia.com
5. википедия. Векторные поля в цилиндрических и сферических координатах. Получено с: en.wikipedia.com

15 основных характеристик живых существ

8 лучших курсов эмоционального интеллекта в Мадриде

Видео:7.9. Задание движения точки в полярных координатахСкачать

Скорость и ускорение точки в цилиндрических координатах

Видео:Построение кривой в полярной системе координатСкачать

Скорость и ускорение точки в цилиндрических координатах

• Цилиндрические оси иногда используются, когда точки перемещаются в пространстве. Они получены путем сложения координат r с полярными координатами на плоскости. Он проходит вдоль неподвижной оси Oz, перпендикулярной плоскости с полярной осью координат (рис. 26). Положение точки М определяется путем установки трех ее цилиндрических координат как функции времени. r = /, (z); f(‘): = A 4.

Вводя понятие времени, мы получаем более сложную науку под названием кинематика, которая связана не с физическими причинами движения, а с геометрической природой движения во взаимосвязи времени. Людмила Фирмаль

Разложение векторов скорости и ускорения на составляющие, параллельные осям цилиндрической системы координат Or, Op, Oz, выражается в виде v = vrr ° + vJ, p0 + vI £; (30) a = arr ° + app ° + ajc, (31) Где r °, p ° и k единичные векторы в направлении вдоль оси цилиндрической системы координат. Оси Ор и Ор находятся в одной плоскости с осями Ох и Оу. Выразите радиус-вектор p точки M как сумму двух векторов. p = OM ‘+ M’ M = rr ° + zk. Скорость точки получается путем дифференцирования вектора радиуса p по времени. Первый член этой формулы был рассчитан при выводе формулы для скорости полярной точки (24). прибывший (D / dz) (rr °) = rr ° +/ r = r; 1> p = rf; t>. = z. (33).

• Компоненты скорости t> r, vp и v. Параллельно оси цилиндрической системы координат и перпендикулярно друг другу, Ускорение точки получается путем дифференцирования вектора скорости по времени. Первый член в этом уравнении был рассчитан, когда ускорение было получено в полярных координатах. ^ (R0 + rfr0) = (r-rf2) r ° + (rf + 2rf) p0 Второе слагаемое в дифференцировании проходит вектор k по знаку производной.

Доказано, что две пары сил в плоскости, пересекающиеся с силой, действующей на один и тот же объект, могут быть заменены одной эквивалентной парой сил векторного момента, равной сумме векторных моментов пары заданных сил. Людмила Фирмаль

Объедините производные результаты, чтобы получить следующее разложение ускорения на компоненты, параллельные осям цилиндрической системы координат. a = (r-rf2) r0 + (rf + 2rf) p ° 4-2. (34) По сравнению с (31) получена проекционная формула ускорения по цилиндрической координатной оси. ar = r gp2; ar = gf + 2gf; az = z. (35) Компоненты ускорения a, ar и ar перпендикулярны друг другу, поэтому a = y / ai + aj + al = h / (r-rf2) 24(rf + 2rf) 2 + r2.

Если вам потребуется помощь по теоретической механике вы всегда можете написать мне в whatsapp.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

🌟 Видео

Сферические координатыСкачать

Определение координаты движущегося тела | Физика 9 класс #3 | ИнфоурокСкачать

Объем параболоида: тройной интеграл в цилиндрической системе координатСкачать

Уравнение равномерного прямолинейного движения | Физика 10 класс #3 | ИнфоурокСкачать

Уравнение теплопроводности в цилиндрических координатахСкачать

§56 Сферическая система координатСкачать