Уравнение движения в сферической системе координат (2 видео)

Скорость и ускорение в сферических координатах

Содержание

Скорость и ускорение в сферических координатах
Скорость и ускорение в сферических координатах
Готовые работы на аналогичную тему
Скорость и ускорение в сферических координатах
Вектор скорости
Ускорение системы
📺 Видео

Видео:Уравнение движенияСкачать

Скорость и ускорение в сферических координатах

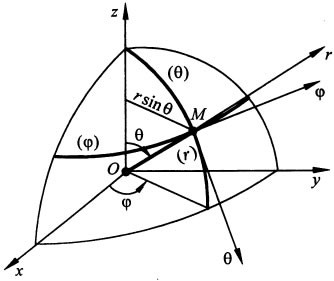
В качестве примера использования полученной формулы рассчитайте скорость и ускорение точки в сферических координатах. Сферические координаты точки M представляют собой величины r, φ, 0 (рис. 27).

Мы видели, что кривая тотализатора Кроноса определена в константе, то есть тотализатор кронизма определен в одной и той же точке тотализатора кронизма для обоих законов. Людмила Фирмаль

Координатная линия r — это линия (g) с базисным вектором ei. (Координатная линия р параллельна сфере с базовым вектором Линия координат 0 — это меридиан сферы с базисным вектором ee. Базисные векторы оказались ортогональными. Декартовы координаты x, y, z точки M, проходящей через сферу, выражаются следующим соотношением. x = rcos0cos r2 + t ^ + T’e = r2 + r292cos20 + r202; T = | я? 2 = i (r2 + r2v2cos20 + r202).

Проекция осевого ускорения, направленная вдоль базисного вектора, рассчитывается с использованием уравнения (49). У нас есть 1 а ‘= ч. f (52) = — (G2 6) + gf2 cos0 sin 0. g dt О векторе ускорения a = arer + a9ev + ahee. Модуль ускорения имеет следующую формулу: a = y / a ^ + a1 + a. » Точно так же вы можете рассчитать скорость и ускорение ранее полученных цилиндрических координатных точек.

Эта последняя ситуация сохраняется для объема, заключенного во вторичную плоскость, и двух параллельных плоскостей для части вращающегося тела, окруженной между двумя плоскостями, перпендикулярными оси. Людмила Фирмаль

Для определения неизвестной силы в равновесном состоянии предпочтительнее использовать равновесное состояние системы сходящихся сил в аналитической форме. Таким образом, квадрат каждого значения подкоркового выражения равен нулю, поэтому само значение равно нулю.

Если вам потребуется помощь по теоретической механике вы всегда можете написать мне в whatsapp.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

Видео:Часть 1. Скорость и ускорение в сферической системе координатСкачать

Скорость и ускорение в сферических координатах

Вы будете перенаправлены на Автор24

Движение точки в пространстве можно считать заданным, если известны законы изменнеия трех ее декартовых координат x, y, z как функции времени. Однако в некоторых случаях пространственного движения материальных точек (например, в областях, ограниченных поверхностями различной формы) использование уравнений движения в декартовых координатах неудобно, так как они становятся слишком громоздкими. В таких случаях можно выбрать другие три независимых скалярных параметра $q_1,_2, q_3$, называемых криволинейными, или обобщенными координатами, которые также однозначно определяют положение точки в пространстве.

Скорость точки М при задании ее движения в криволинейных координатах определится в виде векторной суммы составляющих скоростей, параллельных координатным осям:

Проекции вектора скорости на соответствующие координатные оси равны: $v_=overlinecdot overline=H_idot , i=overline$

Здесь $H_i=left|<left(frac<partial overrightarrow>right)>_Mright|$ — параметр, который называется i-м коэффициентом Ламе и равен значению модуля частной производной от радиус-вектора точки по i-ой криволинейной координате, вычисленной в данной точке М. Каждый из векторов $overline$ имеет направление, соответствующее направлению движения точки конца радиус-вектора $r_i$ при возрастании i-й обобщенной координаты. Модуль скорости в ортогональной криволинейной системе координат можно рассчитать по зависимости:

В приведенных формулах значения производных и коэффициентов Ламе вычисляют для текущего положения точки М в пространстве.

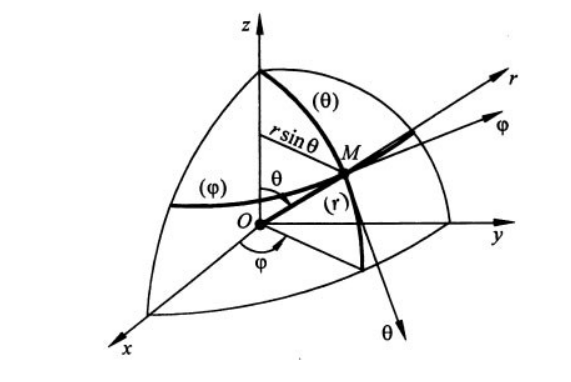
Координатами точки в сферической системе координат являются скалярные параметры r, $, $, отсчитываемые так, как показано на рис. 1.

Рисунок 1. Вектор скорости в сферической системе координат

Система уравнений движения точки в данном случае имеет вид:

[left< begin r=r(t) \ varphi =varphi (t \ theta =theta (t end right.]

На рис. 1 изображены радиус-вектор r, проведенный из начала координат, углы $$ и $$, а также координатные линии и оси рассматриваемой системы в произвольной точке М траектории. Видно, что координатные линии $()$ и $()$ лежат на поверхности сферы радиусом r. Данная криволинейная система координат также является ортогональной. Декартовы координаты могут быть выражены через сферические координаты так:

[x=rcosvarphi sintheta ; y=rsinvarphi costheta ; z=rcostheta ]

Тогда коэффициенты Ламе: $H_r=1; H_=rsinvarphi ; H_0=r$ ; проекции скорости точки на оси сферической системы координат $v_r=dot;$ $v_=rdot$; $ v_=rdotsintheta $, а модуль вектора скорости

Ускорение точки в сферической системе координатат

проекции ускорения точки на оси сферической системы координат

Готовые работы на аналогичную тему

Точка движется по линии пересечения сферы и цилиндра согласно уравнениям: r = R, $varphi $ = kt/2, $theta $ = kt/2 , (r, $varphi $, $theta $ — сферические координаты). Найти модуль и проекции скорости точки на оси сферической системы координат.

Найдём проекции вектора скорости на оси сферических координат:

Используя условие задачи 1, определить модуль ускорения точки.

Найдём проекции вектора ускорения на оси сферических координат:

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 16 11 2021

Видео:Сферические координатыСкачать

Скорость и ускорение в сферических координатах

Движение в пространстве может быть задано, если известен закон изменения трех декартовых координат x , y , z в качестве функции времени.

Имеются случаи, когда перемещение материальной точки не может быть описано с помощью уравнения движения в декартовых координатах, так как запись становится громоздкой. Тогда следует выбирать три независимые скалярные параметра q 1 , q 2 , q 3 , называемые криволинейными (обобщенными) координатами, которые способны четко определить положение точки в пространстве.

Видео:Уравнение координат при равноускоренном движенииСкачать

Вектор скорости

Определение точки М во время задания ее движения в криволинейных координатах возможно в виде векторной суммы составляющих скоростей, параллельных координатным осям:

υ = d r → d t = ∂ r → ∂ q 1 q ˙ 1 + ∂ r → ∂ q 2 q ˙ 2 + ∂ r → ∂ q 3 q ˙ 3 = υ q 1 e 1 ¯ + υ q 2 e 2 ¯ + υ q 3 e 3 ¯ .

Запись проекции вектора скорости на соответствующие координаты оси примет вид:

υ q i = υ ¯ · e i ¯ = H i q i ˙ , i = 1 , 3 .

H i = ∂ r → ∂ q i M является параметром, называющимся i — м коэффициентом Ламе и равняющимся значению модуля частной производной от радиус-вектора точки по i — ой криволинейной координате, которая была вычислена в данной точке М .

Направление каждого из векторов e i соответствует направлению движения точки конца радиус-вектора r i при возрастании i — й обобщенной координаты.

Расчет модуля скорости в ортогональной криволинейной системе координат рассчитывается по формуле:

υ = υ q 1 2 + υ q 2 2 + υ q 3 2 = H 1 2 q ˙ 1 2 + H 2 2 q ˙ 2 2 + H 3 2 q ˙ 3 2 .

Чтобы вычислить текущее положение точки М , необходимо найти производные и коэффициенты Ламе приведенных формул в пространстве.

В сферической системе координат координатами точки являются скалярные параметры r , φ , θ , отсчитываемые так, как изображено на рисунке 1 .

Рисунок 1 . Вектор скорости в сферической системе координат

Видео:Физика - уравнения равноускоренного движенияСкачать

Ускорение системы

Составленная система уравнений движения точки запишется как:

r = r ( t ) φ = φ ( t ) θ = θ ( t ) .

На рисунке 1 показаны радиус-вектор, проведенный из начала координат, углы φ и θ , координатные линии, оси рассматриваемой системы в произвольной точке М траектории.

Расположение координатных линий ( φ ) и ( θ ) идет на поверхности сферы радиусом r . Данная система получила название ортогональной.

Выражение декартовых координат возможно через сферические:

x = r cos φ sin θ ; y = r sin φ cos θ ; z = r cos θ .

Отсюда следует, что коэффициенты Ламе H r = 1 ; H φ = r sin φ ; H 0 = r , проекции скорости точки на оси сферической системы координат υ r = r ˙ ; υ θ = r θ ˙ ; υ φ = r φ ˙ sin θ , а модуль вектора скорости υ = υ r 2 + υ φ 2 + υ θ 2 = r ˙ 2 + r 2 φ ˙ 2 + r 2 θ ˙ 2 .

Запись ускорения в сферических координатах примет вид:

a → = a r e r → + a φ e φ → + a θ e θ → .

А проекции ускорения точки:

a r = r ˙ — r θ ˙ 2 + φ ˙ 2 sin 2 φ ; a φ = r φ ¨ sin φ + 2 r φ ˙ ( sin θ + θ ˙ cos θ ) ; a θ = r θ ¨ — r φ ˙ 2 sin θ cos θ + 2 r ˙ θ ˙ .

Изображение модуля ускорения будет равняться a = a r 2 + a φ 2 + a θ 2 .

Задана точка, которая производит движение по линии пересечения сферы и цилиндра по уравнению r = R , φ = k t 2 , θ = k t 2 , где r , φ , θ являются сферическими координатами.

Произвести поиск модуля и проекции скорости точки на оси сферической системы координат.

Необходимо найти проекции вектора скорости на оси сферических координат.

υ r = r ˙ = 0 ; υ φ = r φ ˙ sin θ = R k 2 sin k t 2 ; υ θ = r θ ˙ = R k 2 .

Определяем модуль скорости:

υ = υ r 2 + υ φ 2 + υ θ 2 = R k 2 sin 2 k t 2 + 1 .

Применив условие предыдущего задания, определить модуль ускорения точки.

Произведем нахождение проекции вектора ускорения на оси сферических координат.

a r = r ˙ — r θ ˙ 2 + φ ˙ 2 sin 2 φ = R k 2 4 1 + sin 2 k t 2 ; a φ = r φ ¨ sin φ + 2 r φ ˙ sin θ + θ ˙ cos θ = — R k 2 2 sin k t 2 ; a θ = r θ ¨ — r φ ˙ sin θ cos θ + 2 r ˙ θ ˙ = — R k 2 4 sin θ cos k t 2 .

Далее определим модуль ускорения: a = a r 2 + a φ 2 + a θ 2 = R k 2 4 4 + sin 2 k t 2 .

Ответ: a = R k 2 4 4 + sin 2 k t 2