Уравнение движения твердого тела закрепленного на оси

В работе испoльзуются два способа экспериментального определения момента инерции. Первый основан на использовании зависимости периода колебаний физического маятника от его момента инерции.Второй — на анализе инерционных свойств твердого тела, закрепленного на оси, при его вращательном движении. Кроме этого, проводится прямой расчет момента инерции исследуемого тела известной геометрии.

Уравнение вращательного движения для твердого тела, закрепленного на оси, имеет вид

. (4.1)где J — момент инерции твердого тела относительно оси вращения, — его угловое ускорение, M— момент внешних сил, приложенных к телу.
Величина момента инерции относительно какой-либо оси определяется пространственным распределением массы тела. В частности, для тела, состоящего из конечного числа элементарных (малых) масс m_i .

. (4.2)где расстояние от элементарной массы до оси вращения. В общем случае, для сплошных тел, суммирование заменяется интегрированием:

Для некоторых тел простой формы, возможен прямой расчет момента инерции. При сложной форме тела и неравномерном распределении его плотности аналитический расчет величины момента инерции может стать достаточно сложной задачей.
В данной работе применяются два способа экспериментального определения момента инерции: с помощью анализа колебаний физического маятника, составной частью которого является исследуемое тело, и с помощью изучения вращательного движения этого тела.
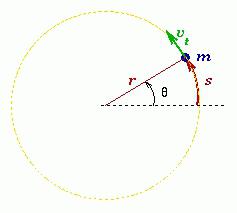
Определение момента инерции твердого тела на основе анализа его колебаний как физического маятника. Если закрепить исследуемое тело А на горизонтальной оси O, проходящей через центр масс (рис.12), то момент сил тяготения будет равен нулю, и тело остается в состоянии безразличного равновесия. Если теперь закрепить на исследуемом теле на некотором удалении L от оси малое тело В с известной массой m, то равновесие перестанет быть безразличным — при равновесии момент силы тяжести, действующий на тело В будет равен нулю. Такую систему тел можно рассматривать как физический маятник.
Уравнение движения такого маятника имеет вид

. (4.3)где J,J_B — моменты инерции твердого тела А и дополнительного грузика B относительно оси O, g-ускорение свободного падения, угол отклонения тела от положения равновесия, — его угловое ускорение.
Если углы отклонения малы , то можно записать

. (4.4)Данное уравнение является уравнением собственных (свободных) гармонических колебаний, его решение имеет вид

. (4.5)где — собственная циклическая частота, T -период колебаний, ₀ — амплитуда колебаний ₀ -начальная фаза колебаний.
Дважды дифференцируя соотношение (4.5) по времени, получаем

. (4.6)Сопоставляя (4.4) и (4.6), находим, что

. (4.7)В связи с тем, что размеры малого тела В во много раз меньше расстояния до оси L, можно считать его материальной точкой и положить

. (4.8)Тогда из уравнений (4.7) и (4.8) получаем

. (4.9)Таким образом, для определения момента инерции твердого тела можно закрепить его на оси, проходящей через центр масс, установить на нем добавочное малое тело с известной массой, измерить период колебаний и зная расстояние L, по формуле (4.9) определить неизвестный момент инерции.
Отметим, что при выводе соотношения (4.9) не учитывалось влияние момента сил трения (M_тр ) в оси. Это приближение обусловлено тем, что при достаточно малом M_тр его воздействие приводит прежде всего к постепенному уменьшению амплитуды колебаний и практически не влияет на их период.

Определение момента инерции твердого тела на основе анализа его равноускоренного вращательного движения. Рассмотрим, как и в предыдущем случае тело А, закрепленное на оси O, проходящей через центр масс (рис.13). Соосно с телом закреплен цилиндр С, на который наматывается нить с прикрепленным к ней грузом В.
Под действием силы тяжести груз будет опускаться, приводя исследуемое тело А во вращение. Уравнение движения груза В, уравнение вращательного движения тела А и уравнение кинематической связи имеют вид

. (4.10) . (4.11) . (4.12)где m-масса груза В, J-момент инерции исследуемого тела вместе с цилиндром C, g — ускорение силы тяжести, T-натяжение нити, r-радиус цилиндра, на который намотана нить, M_тр -момент сил трения, a-ускорение тела В.
Из уравнений (4.10) -(4.12) получаем

. (4.13)Таким образом, если известно ускорение груза В и момент сил трения в оси, то по формуле (4.13) мы можем определить момент инерции исследуемого тела.
Предположим, что груз начинает опускаться с отметки x₀=0, а мы измеряем время t прохождения его между двумя точками x₀ и x₁. Движение грузика в участке x₁-x₂. является равноускоренным, и можно записать

. (4.14) . (4.15)где t₁ -время прохождения участка x₁-x₀, t — время прохождения участка x₂-x₁.
Из (4.14) и (4.15) следует:

. (4.16)Решая это уравнение относительно ускорения a, находим

. (4.17)Таким образом, для определения a нам нужно знать x₀,x₁,x₂ и время t прохождения грузика между точками с координатами x₁ и x₂.
Рассмотрим соотношения, позволяющие определить момент сил трения. При опускания груза с отметки x₀ на полную длину нити до отметки x₃ его потенциальная энергия переходит в кинетическую и в некоторое количество тепловой энергии, по величине равное работе сил трения,

. (4.18)где Ф — полный угол поворота тела при его опускании, E_k — кинетическая энергия системы в нижней точке. Предполагается, что момент силы трения при движении остается постоянной, т.е. не зависит от скорости.
После того, как груз опустится на полную длину нити до отметки x₃ , тело будет продолжать вращаться, и нить начнет наматываться на цилиндр. В результате груз поднимется до отметки x₄. Очевидно,

. (4.19)гдеФ — полный угол поворота тела при подъеме груза.
Учитывая, что , получаем величину момента силы трения

. (4.20)

Установка представляет собой сплошное колесо (рис. 14), которое может вращаться вокруг горизонтальной оси ( для упражнения 1 AVI (2.6M) и для упражнения 2 AVI (5.5M) ). К цилиндру, расположенному на оси колеса, с помощью нити прикреплен груз. Помещая груз в устройство для его крепления, получаем физический маятник, который может колебаться около положения равновесия. Угол отклонения может быть определен по угломерной шкале. В том случае, когда груз освобожден (при этом устройство для его крепления снимается с колеса), под действием силы тяжести он начнет опускаться, приводя колесо во вращение. Установка снабжена системами регистрации периода колебаний колеса и времени опускания груза.
Для регистрации периода колебаний на колесе симметрично расположены два легких одинаковых по массе тела C₁ и C₂ . На теле C₁ закреплен стержень, являющийся составной частью системы измерения периода колебаний. В исходном положении система зафиксирована с помощью фрикционной муфты, управляемой электромагнитом ( при таком положении муфты светится лампа индикации на кнопке управления электромагнитом). При выключении электромагнита фрикционная муфта освобождает колесо, и оно начинает движение (колебательное или вращательное). Время колебаний колеса определяется с помощью электронного таймера. Время перемещения груза при вращательном движении колеса определяется с помощью того же таймера, включение и выключение которого в этом случае осуществляется оптическими датчиками. Эти датчики крепятся на кронштейнах и могут фиксироваться на различных высотах. Положение датчиков определяется с помощью линейки (рис.14)
Запуск таймера в режиме измерения периодов колебаний осуществляется нажатием кнопки «Пуск», остановка — кнопкой «Стоп». При измерении времени опускания груза нажимают на кнопку «Пуск», после чего на индикаторе электронного таймера высвечивается время прохождения груза между двумя датчиками положения. Переключение таймера в тот или иной режим работы осуществляется тумблером «Колеб.- Вращ.». При подготовке к дальнейшим измерениям результаты предыдуших убираются с табло нажатием кнопки «Сброс».

Проведение эксперимента
Упражнение 1. Определение момента инерции колеса методом колебаний.

На краю колеса закрепляют устройство для крепления груза, в которое устанавливают груз, колесо выводят из положения равновесия на угол, не превышающий 10 0 . Определяют время t_n полных колебаний n=10 : 15. Такое измерение проводят 3-5 раз. Результаты измерений времени заносятся в табл.4.1.

После этого не менее трех раз измеряют расстояние L от оси вращения до центра масс груза ( это есть расстояние от оси вращения до центра винта, закрепляющего устройство крепления груза на колесе). Результаты заносятся в табл.4.1.

Взвешивают устройство для крепления груза и сам груз. Значения масс тел m_к и m_гр заносят в табл.4.1.

Таблица 4.1

N	n	tn	TN	ST	LN	SL	mк , mг	J	SJ
1
2
3
4
5

По экспериментальным данным вычислить выборочные средние значения (средние арифметические значения) величин периода Т и расстояния L.

Вычислить выборочные стандартные отклонения (среднеквадратичные ошибки среднего арифметичсекого) для Т и L

По полученным данным, пользуясь уравнением (4.9) и учитывая, что m=m_к+m_гр, определяют момент инерции колеса J.

Оценить погрешности для J, используя следующую формулу для расчета погрешностей косвенных измерений:

. (4.21)где S_m дана в описании используемых весов, а S_g находится из таблиц физических постоянных.

Упражнение 2. Определение момента инерции колеса методом вращения.

Снять с колеса устройство для крепления груза.

Измерить время t прохождения груза между отметками x₁ и x₂. Измерения провести не менее 5-7 раз для фиксированных значений x₀,x₂ и разных x₁, каждый раз занося данные в табл.4.2. Измеряют также координату x₃ точки, до которой опускается груз при полностью размотанной нити и координату x₄ точки, до которой поднимается груз при дальнейшем наматывании нити на цилиндр, пока колесо продолжает свободно вращаться.

Несколько раз измерить радиус r цилиндра, на который наматывается нить.

Таблица 4.2

N	x1	x2	#t	aN	Sa	x0	x3	x4	Mтр	SM
1
2
3

По формулам (4.17) и (4.20) определить ускорения a_N и моменты сил трения M_тр для каждого измерения. Результаты измерений заносятся в табл.4.2.

Поскольку a_N и M_тр определяются для различных значений x₁, то будем считать полученные значения ускорений и моментов сил трения независимыми. Найти выборочные средние значения ускорения и момента сил трения и выборочные стандартные отклонения этих величин. Результаты вычислений занести в табл.4.2.

Вычислить выборочное среднее значение радиуса цилиндра и среднеквадратичную ошибку этой величины.

По формуле (4.13 ) определить значение момента инерции колеса и его погрешность.

Упражнение 3. Прямой расчет момента инерции колеса

Используемое в установке колесо можно представить как совокупность тел простой формы (рис.15), диска радиуса R₁, толщины l₁ ; обода толщины l₂ с внешним и внутренним радиусами R₂,R₁; двух малых тел C₁ и C₂, расположенных на расстоянии R₃ от оси; цилиндра, имеющего радиус R₄ и толщину l₃. Для всех этих тел момент инерции можно рассчитать.
Известно, что момент инерции диска массы m_д относительно оси равен (см. Приложение 4)

. (4.22)а для обода массы m_об (см.Приложение 5)

. (4.23)Учитывая, что диск, обод и цилиндр сделаны из одного материала с плотностью , получаем окончательно выражение для момента инерции колеса

. (4.24)где m_c — суммарная масса тел C₁ и C₂.
С помощью штангенциркуля и линейки определяют геометрические размеры каждой выделенной части колеса по несколько раз. Результаты измерений заносят в таблицу 4.3.

Таблица 4.3

N	1	2	3	4	5
R 1n
S R 1
R 2n
S R 2
R 3n
S R 3
R 4n
S R 4

N	1	2	3	4	5
l 1n
S l 1
l 2n
S l 2
l 3n
S l 3

Вычисляют выборочные стандартные отклонения для этих величин. Результаты заносят в таблицу 4.3.

По формуле (4.24) рассчитывают значение момента инерции колеса и определяют погрешность.

Рассчитанное значение момента инерции колеса сравнивают с значениями, полученными экспериментально в упражнениях 1 и 2.

Основные итоги работы
В процессе выполнения работы должен быть определен момент инерции колеса двумя способами. Следует сопоставить эти результаты с величиной вычисленного по (4.24) момента инерции.
Контрольные вопросы

Что такое главные оси инерции? Центральные оси? Привести примеры.

Что такое момент инерции тела относительно закрепленной оси?

Чему равны моменты инерции следующих тел: тонкая палочка, тонкий диск, тонкие прямоугольная и треугольная пластины, цилиндр, шар, параллелепипед? Как их получить?

Сформулируйте теорему Гюйгенса-Штейнера.

Литература

Алешкевич В.А., Деденко Л.Г., Караваев В.А. Механика твердого тела. Лекции (Университетский курс общей физики). М.: Изд-во физического факультета МГУ, 1998.

Видео:Основное уравнение динамики вращательного движения. 10 класс.Скачать



Вращение твердого тела

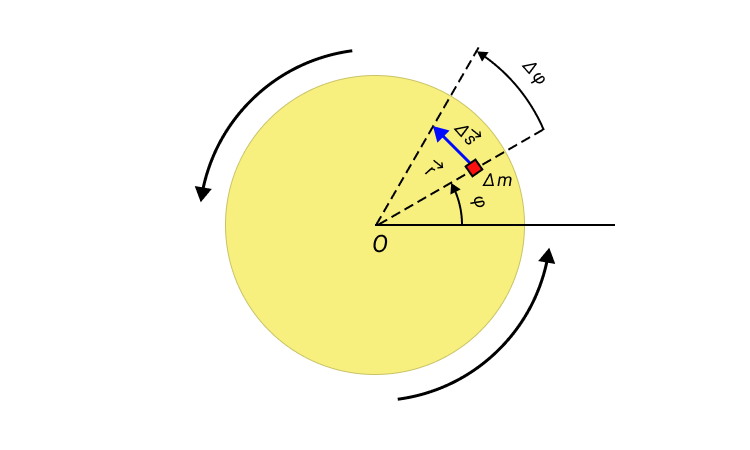
Для кинематического описания процесса вращения твердого тела нужно ввести такие понятия как угловое перемещение Δ φ , угловое ускорение ε и угловая скорость ω :

ω = ∆ φ ∆ t , ( ∆ t → 0 ) , ε = ∆ φ ∆ t , ( ∆ t → 0 ) .

Углы выражаются в радианах. За положительное направление вращения принимается направление против часовой стрелки.

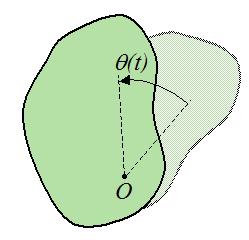
Когда твердое тело вращается относительно неподвижной оси, все точки этого тела перемещаются с одинаковыми угловыми скоростями и ускорениями.



Рисунок 1. Вращение диска относительно оси, проходящей через его центр O .

Если угловое перемещение Δ φ мало, то модуль вектора линейного перемещения ∆ s → некоторого элемента массы Δ m вращающегося твердого тела можно выразить соотношением:

в котором r – модуль радиус-вектора r → .

Между модулями угловой и линейной скоростей можно установить связь посредством равенства

Модули линейного и углового ускорения также взаимосвязаны:

Векторы v → и a → = a τ → направлены по касательной к окружности радиуса r .

Также нам необходимо учесть возникновение нормального или центростремительного ускорения, которое всегда возникает при движении тел по окружности.

Модуль ускорения выражается формулой:

a n = v 2 r = ω 2 r .

Если разделить вращающееся тело на небольшие фрагменты Δ m i , обозначить расстояние до оси вращения через r i , а модули линейных скоростей через v i , то запись формулы кинестетической энергии вращающегося тела будет иметь вид:

E k = ∑ i ν m v i 2 2 = ∑ i ∆ m ( r i ω ) 2 2 = ω 2 2 ∑ i ∆ m i r i 2 .

Физическая величина ∑ i ∆ m i r i 2 носит название момента инерции I тела относительно оси вращения. Она зависит от распределения масс вращающегося тела относительно оси вращения:

I = ∑ i ∆ m i r i 2 .

В пределе при Δ m → 0 эта сумма переходит в интеграл. Единица измерения момента инерции в С И – килограмм—метр в квадрате ( к г · м 2 ) . Таким образом, кинетическую энергию твердого тела, вращающегося относительно неподвижной оси, можно представить в виде:

В отличие от выражения, которое мы использовали для описания кинестетической энергии поступательно движущегося тела m v 2 2 , вместо массы m в формулу входит момент инерции I . Также мы принимаем во внимание вместо линейной скорости v угловую скорость ω .

Если для динамики поступательного движения основную роль играет масса тела, то в динамике вращательного движения имеет значение момент инерции. Но если масса – это свойство рассматриваемого твердого тела, которое не зависит от скорости движения и других факторов, то момент инерции зависит от того, вокруг какой оси вращается тело. Для одного и того же тела момент инерции будет определяться различными осями вращения.

В большинстве задач считается, что ось вращения твердого тела проходит через центр его массы.

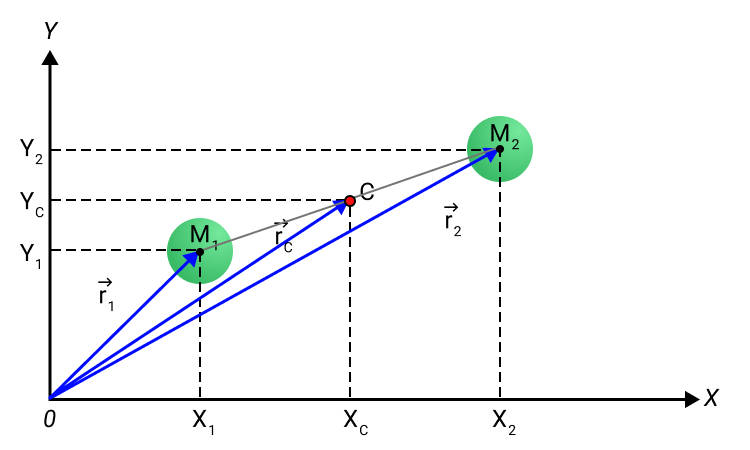
Положение x C , y C центра масс для простого случая системы из двух частиц с массами m 1 и m 2 , расположенными в плоскости X Y в точках с координатами x 1 , y 1 и x 2 , y 2 определяется выражениями:

x C = m 1 x 1 + m 2 x 2 m 1 + m 2 , y C = m 1 y 1 + m 2 y 2 m 1 + m 2 .



Рисунок 2. Центр масс C системы из двух частиц.

В векторной форме это соотношение принимает вид:

r C → = m 1 r 1 → + m 2 r 2 → m 1 + m 2 .

Аналогично, для системы из многих частиц радиус-вектор r C → центра масс определяется выражением

r C → = ∑ m i r i → ∑ m i .

Если мы имеем дело с твердым телом, состоящим из одной части, то в приведенном выражении суммы для r C → необходимо заменить интегралами.

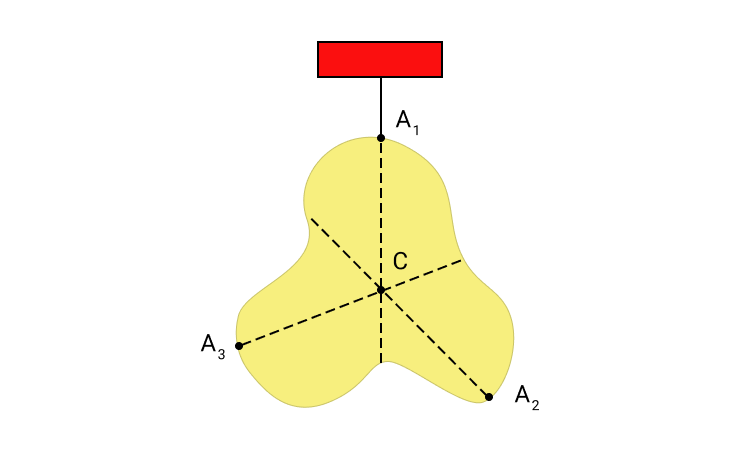
Центр масс в однородном поле тяготения совпадает с центром тяжести. Это значит, что если мы возьмем тело сложной формы и подвесим его за центр масс, то в однородном поле тяготения это тело будет находиться в равновесии. Отсюда следует способ определения центра масс сложного тела на практике: его необходимо последовательно подвесить за несколько точек, одновременно отмечая по отвесу вертикальные линии.



Рисунок 3. Определение положения центра масс C тела сложной формы. A 1 , A 2 , A 3 точки подвеса.

На рисунке мы видим тело, которое подвешено за центр масс. Оно находится в состоянии безразличного равновесия. В однородном поле тяготения равнодействующая сил тяжести приложена к центру масс.

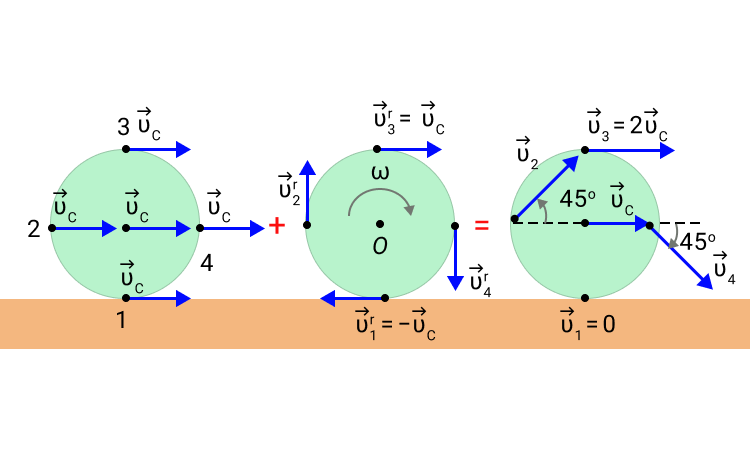
Мы можем представить любое движение твердого тела как сумму двух движений. Первое поступательное, которое производится со скоростью центра масс тела. Второе – это вращение относительно оси, которая проходит через центр масс.

Предположим. Что у нас есть колесо, которое катится по горизонтальной поверхности без проскальзывания. Все точки колеса во время движения перемещаются параллельно одной плоскости. Такое движение мы можем обозначить как плоское.

Видео:Вращательное движение. 10 класс.Скачать



Теорема о движении центра масс

Кинестетическая энергия вращающегося твердого тела при плоском движении будет равна сумме кинетической энергии поступательного движения и кинетической энергии вращения относительно оси, которая проведена через центр масс и располагается перпендикулярно плоскостям, в которых движутся все точки тела:

E k = m v C 2 2 + I C ω 2 2 ,

где m – полная масса тела, I C – момент инерции тела относительно оси, проходящей через центр масс.



Рисунок 4. Качение колеса как сумма поступательного движения со скоростью v C → и вращения с угловой скоростью ω = v C R относительно оси O , проходящей через центр масс.

В механике используется теорема о движении центра масс.

Любое тело или несколько взаимодействующих тел, которые представляют собой единую систему, обладают центром масс. Этот центр масс под воздействием внешних сил перемещается в пространстве как материальная точка, в которой сосредоточена вся масса системы.

На рисунке мы изобразили движение твердого тела, на которое действуют силы тяжести. Центр масс тела движется по траектории, которая близка к параболе, тогда как траектория остальных точек тела является более сложной.



Рисунок 5. Движение твердого тела под действием силы тяжести.

Видео:Вращение тела вокруг неподвижной осиСкачать



Теорема Штейнера о параллельном переносе оси вращения

Рассмотрим случай, когда твердое тело движется вокруг некоторой неподвижной оси. Момент инерции этого тела инерции I можно выразить через момент инерции I C этого тела относительно оси, проходящей через центр масс тела и параллельной первой.



Рисунок 6. К доказательству теоремы о параллельном переносе оси вращения.

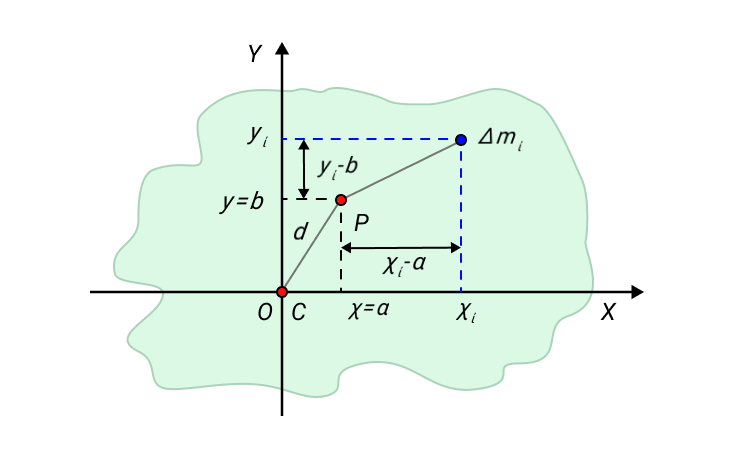
Для примера возьмем твердое тело, форма которого произвольна. Обозначим центр масс С . Выберем систему координат Х У с началом координат 0 . Совместим центр масс и начало координат.

Одна из осей проходит через центр масс С . Вторая ось пересекает произвольно выбранную точку Р , которая расположена на расстоянии d от начала координат. Выделим некоторый малый элемент массы данного твердого тела Δ m i .

По определению момента инерции:

I C = ∑ ∆ m i ( x i 2 + y i 2 ) , I P = ∑ m i ( x i — a ) 2 + y i — b 2

Выражение для I P можно переписать в виде:

I P = ∑ ∆ m i ( x i 2 + y i 2 ) + ∑ ∆ m i ( a 2 + b 2 ) — 2 a ∑ ∆ m i x i — 2 b ∑ ∆ m i y i .

Два последних члена уравнения обращаются в нуль, так как начало координат в нашем случае совпадает с центром масс тела.

Так мы пришли к формуле теоремы Штейнера о параллельном переносе оси вращения.

Для тела, которое вращается относительно произвольной неподвижной оси, момент инерции, согласно теореме Штейнера, равен сумме момента инерции этого тела относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями.

I P = I C + m d 2 ,

где m – полная масса тела.



Рисунок 7. Модель момента инерции.

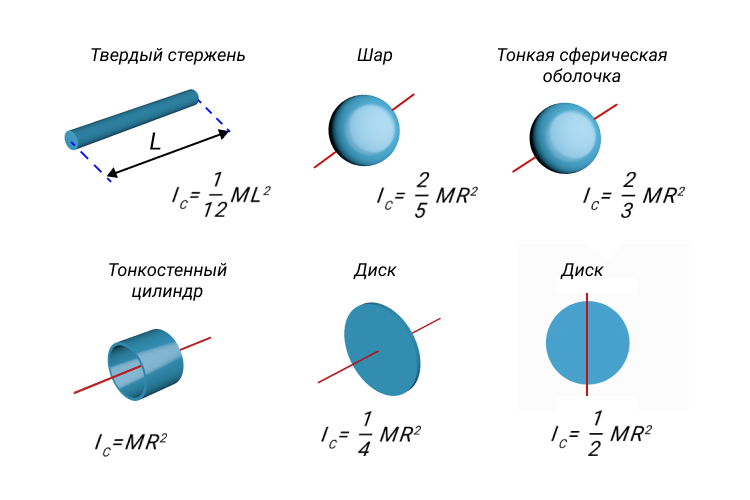
На рисунке ниже изображены однородные твердые тела различной формы и указаны моменты инерции этих тел относительно оси, проходящей через центр масс.



Рисунок 8. Моменты инерции I C некоторых однородных твердых тел.

Видео:Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать



Основное уравнение динамики вращательного движения твердого тела

В тех случаях, когда мы имеем дело с твердым телом, которое вращается относительно неподвижной оси, мы можем обобщить второй закон Ньютона. На рисунке ниже мы изобразили твердое тело произвольной формы, вращающееся относительно некоторой оси, проходящей через точку О . Ось вращения расположена перпендикулярно плоскости рисунка.

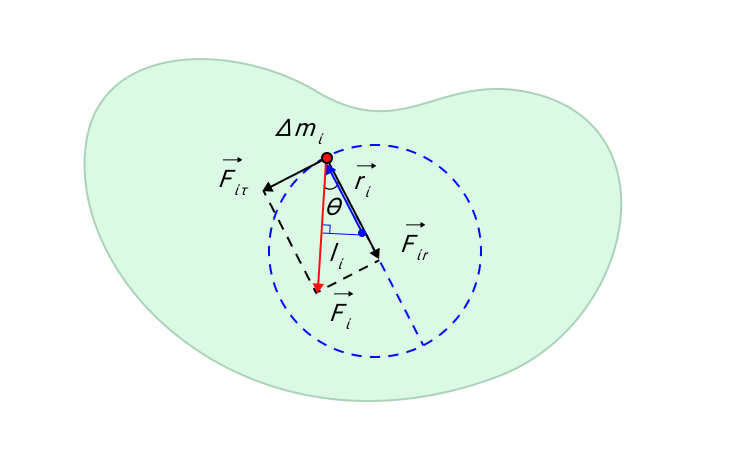
Δ m i – это произвольный малый элемент массы, на который оказывают воздействие внешние и внутренние силы. Равнодействующая всех сил есть F i → . Ее можно разложить на две составляющие: касательную составляющую F i τ → и радиальную F i r → . Радиальная составляющая F i r → создает центростремительное ускорение a n .



Рисунок 9. Касательная F i τ → и радиальная F i r → составляющие силы F i → действующей на элемент Δ m i твердого тела.

Касательная составляющая F i τ → вызывает тангенциальное ускорение a i τ → массы Δ m i . Второй закон Ньютона, записанный в скалярной форме, дает

∆ m i a i τ = F i τ sin θ или ∆ m i r i ε = F i sin θ ,

где ε = a i τ r i – угловое ускорение всех точек твердого тела.

Если обе части написанного выше уравнения умножить на r i , то мы получим:

∆ m i r i 2 ε = F i r i sin θ = F i l i = M i .

Здесь l i – плечо силы, F i , → M i – момент силы.

Теперь нужно аналогичные соотношения записать для всех элементов массы Δm_i вращающегося твердого тела, а затем просуммировать левые и правые части. Это дает:

∑ ∆ m i r i 2 ε = ∑ M i .

Стоящая в правой части сумма моментов сил, действующих на различные точки твердого тела, состоит из суммы моментов всех внешних сил и суммы моментов всех внутренних сил.

∑ M = ∑ M i в н е ш н + ∑ M i в н у т р .

Но сумма моментов всех внутренних сил согласно третьему закону Ньютона равна нулю, поэтому в правой части остается только сумма моментов всех внешних сил, которые мы будем обозначать через M . Так мы получили основное уравнение динамики вращательного движения твердого тела.

Угловое ускорение ε и момент сил M в этом уравнении являются величинами алгебраическими.

Обычно за положительное направление вращения принимают направление против часовой стрелки.

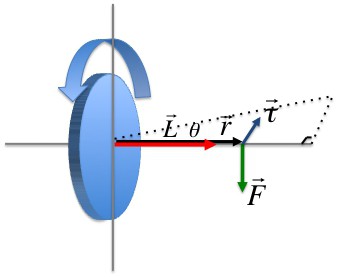
Возможна и векторная форма записи основного уравнения динамики вращательного движения, при которой величины ω → , ε → , M → определяются как векторы, направленные по оси вращения.

Видео:Урок 70. Виды равновесия. Условие равновесия тела при отсутствии вращения.Скачать



Закон сохранения момента импульса

В разделе, посвященном поступательному движению тела, мы ввели понятие импульса тела p → . По аналогии с поступательным движением для вращательного движения мы вводим понятие момента импульса.

Момент импульса вращающегося тела – это физическая величина, которая равняется произведению момента инерции тела I на угловую скорость ω его вращения.

Для обозначения момента импульса используется латинская буква L .

Поскольку ε = ∆ ω ∆ t ; ∆ t → 0 , уравнение вращательного движения можно представить в виде:

M = I ε = I ∆ ω ∆ t или M ∆ t = I ∆ ω = ∆ L .

M = ∆ L ∆ t ; ( ∆ t → 0 ) .

Мы получили это уравнение для случая, когда I = c o n s t . Но оно будет справедливо и тогда, когда момент инерции тела будет изменяться в процессе движения.

Если суммарный момент M внешних сил, действующих на тело, равен нулю, то момент импульса L = I ω относительно данной оси сохраняется: ∆ L = 0 , если M = 0 .

L = l ω = c o n s t .

Так мы пришли к закону сохранения момента импульса.

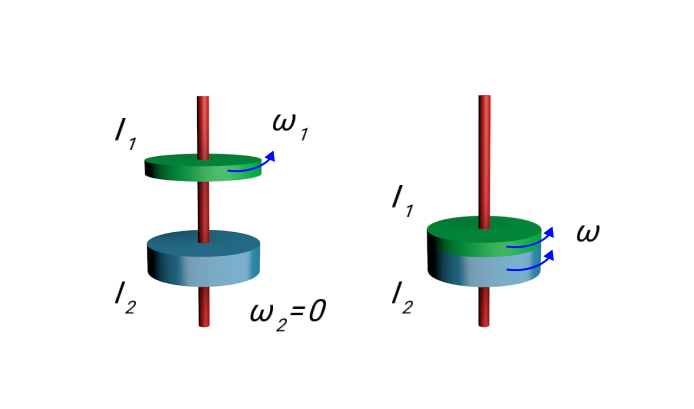
В качестве примера приведем рисунок, на котором изображено неупругое вращательное столкновение дисков, которые насажены на общую для них ось.



Рисунок 10. Неупругое вращательное столкновение двух дисков. Закон сохранения момента импульса: I 1 ω 1 = ( I 1 + I 2 ) ω .

Мы имеем дело с замкнутой системой. Для любой замкнутой системы закон сохранения момента импульса будет справедливым. Он выполняется и в условиях экспериментов по механике, и в условиях космоса, когда планеты движутся по своим орбитам вокруг звезды.

Мы можем записать уравнение динамики вращательного движения как для неподвижной оси, так и для оси, которая перемещается равномерно или с ускорением. Вид уравнения не изменится и в том случае, если ось движется ускоренно. Для этого должно выполняться два условия: ось должна проходить через центр массы тела, а ее направление в пространстве остается неизменным.

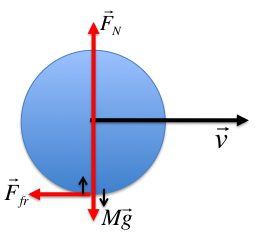
Предположим, что у нас есть тело (шар или цилиндр), которое катится по наклонной плоскости с некоторым трением.



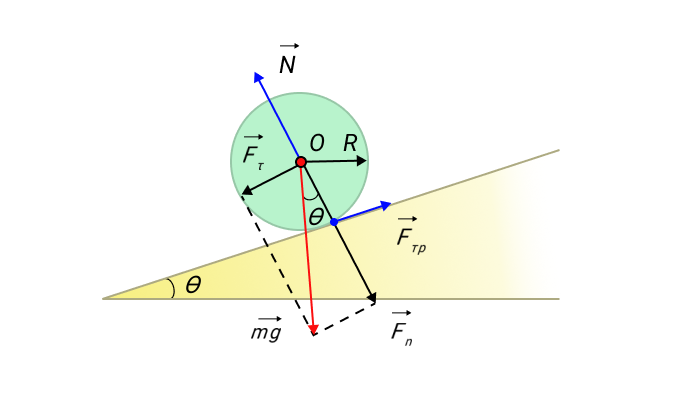
Рисунок 11. Качение симметричного тела по наклонной плоскости.

Ось вращения O проходит через центр масс тела. Моменты силы тяжести m g → и силы реакции N → относительно оси O равны нулю. Момент M создает только сила трения: M = F т р R .

Уравнение вращательного движения:

I C ε = I C a R = M = F т р R ,

где ε – угловое ускорение катящегося тела, a – линейное ускорение его центра масс, I C – момент инерции относительно оси O , проходящей через центр масс.

Второй закон Ньютона для поступательного движения центра масс записывается в виде:

m a = m g sin α — F т р .

Исключая из этих уравнений F т р , получим окончательно:

α = m g sin θ I C R 2 + m .

Из этого выражения видно, что быстрее будет скатываться с наклонной плоскости тело, обладающее меньшим моментом инерции. Например, у шара I C = 2 5 m R 2 , а у сплошного однородного цилиндра I C = 1 2 m R 2 . Следовательно, шар будет скатываться быстрее цилиндра.

Видео:Урок 74. Равновесие тела с закрепленной осью вращенияСкачать



Вращательное движение тела. Закон вращательного движения

В этой статье описывается важный раздел физики — «Кинематика и динамика вращательного движения».

Видео:Урок 93. Основное уравнение динамики вращательного движенияСкачать



Основные понятия кинематики вращательного движения

Вращательным движением материальной точки вокруг неподвижной оси называют такое движение, траекторией которого является окружность, находящаяся в плоскости перпендикулярной к оси, а центр ее лежит на оси вращения.

Вращательное движение твердого тела — это движение, при котором по концентрическим (центры которых лежат на одной оси) окружностям движутся все точки тела в соответствии с правилом для вращательного движения материальной точки.

Пусть произвольное твердое тело T совершает вращения вокруг оси O, которая перпендикулярна плоскости рисунка. Выберем на данном теле точку M. При вращении эта точка будет описывать вокруг оси O круг радиусом r.



Через некоторое время радиус повернется относительно исходного положения на угол Δφ.

За положительное направление поворота принято направление правого винта (по часовой стрелке). Изменение угла поворота со временем называется уравнением вращательного движения твердого тела:

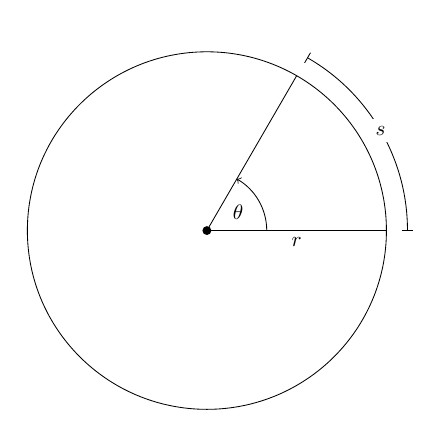
Если φ измерять в радианах (1 рад — это угол, соответствующий дуге, длиной равной ее радиусу), то длина дуги окружности ΔS, которую пройдет материальная точка M за время Δt, равна:

Видео:Уравнение движенияСкачать



Основные элементы кинематики равномерного вращательного движения

Мерой перемещения материальной точки за небольшой промежуток времени dt служит вектор элементарного поворота dφ.



Угловая скорость материальной точки или тела — это физическая величина, которая определяется отношением вектора элементарного поворота к продолжительности этого поворота. Направление вектора можно определить правилом правого винта вдоль оси О. В скалярном виде:

Если ω = dφ/dt = const, то такое движение называется равномерное вращательное движение. При нем угловую скорость определяют по формуле

Согласно предварительной формуле размерность угловой скорости

Равномерное вращательное движение тела можно описать периодом вращения. Период вращения T — физическая величина, определяющая время, за которое тело вокруг оси вращения выполняет один полный оборот ([T] = 1 с). Если в формуле для угловой скорости принять t = T, φ = 2 π (полный один оборот радиуса r), то

поэтому период вращения определим следующим образом:

Число оборотов, которое за единицу времени совершает тело, называется частотой вращения ν, которая равна:

Единицы измерения частоты: [ν]= 1/c = 1 c -1 = 1 Гц.

Сравнивая формулы для угловой скорости и частоты вращения, получим выражение, связывающее эти величины:

Видео:Вращательное движение твёрдого тела. Задачи 1, 2, 3Скачать



Основные элементы кинематики неравномерного вращательного движения

Неравномерное вращательное движение твердого тела или материальной точки вокруг неподвижной оси характеризует его угловая скорость, которая изменяется со временем.

Вектор ε, характеризующий скорость изменения угловой скорости, называется вектором углового ускорения:



Если тело вращается, ускоряясь, то есть dω/dt > 0, вектор имеет направление вдоль оси в ту же сторону, что и ω.

Если вращательное движение замедлено — dω/dt 2 /r = ω 2 r 2 /r.

Итак, в скалярном виде

Тангенциальное ускоренной материальной точки, которая выполняет вращательное движение

Видео:Уравнение движения тела дано в виде x=2−3t. ВычислиСкачать



Момент импульса материальной точки

Векторное произведение радиуса-вектора траектории материальной точки массой m_i на ее импульс называется моментом импульса этой точки касательно оси вращения. Направление вектора можно определить, воспользовавшись правилом правого винта.

Момент импульса материальной точки (L_i) направлен перпендикулярно плоскости, проведенной через r_i и υ_i, и образует с ними правую тройку векторов (то есть при движении с конца вектора r_i к υ_i правый винт покажет направление вектора L_i).



В скалярной форме

Учитывая, что при движении по кругу радиус-вектор и вектор линейной скорости для i-й материальной точки взаимно перпендикулярные,

Так что момент импульса материальной точки для вращательного движения примет вид

Видео:Физика 10 класс (Урок№5 - Поступательное движение. Вращательное движение твердого тела.)Скачать



Момент силы, которая действует на i-ю материальную точку

Векторное произведение радиуса-вектора, который проведен в точку приложения силы, на эту силу называется моментом силы, действующей на i-ю материальную точку относительно оси вращения.

В скалярной форме

Величина l_i, равная длине перпендикуляра, опущенного из точки вращения на направление действия силы, называется плечом силы F_i.

Видео:§2.2. Вращение твердого тела вокруг неподвижной оси.Скачать



Динамика вращательного движения

Уравнение динамики вращательного движения записывается так:

Формулировка закона следующая: скорость изменения момента импульса тела, которое совершает вращение вокруг неподвижной оси, равна результирующему моменту относительно этой оси всех внешних сил, приложенных к телу.

Видео:Вращательное движение твердого телаСкачать



Момент импульса и момент инерции

Известно, что для i-й материальной точки момент импульса в скалярной форме задается формулой

Если вместо линейной скорости подставить ее выражение через угловую:

то выражение для момента импульса примет вид

Величина I_i = m_ir_i 2 называется моментом инерции относительно оси i-й материальной точки абсолютно твердого тела, проходящей через его центр масс. Тогда момент импульса материальной точки запишем:

Момент импульса абсолютно твердого тела запишем как сумму моментов импульса материальных точек, составляющих данное тело:

Видео:Урок 96. Простейшие задачи на вращение твердого телаСкачать



Момент силы и момент инерции

Закон вращательного движения гласит:

Известно, что представить момент импульса тела можно через момент инерции:

Учитывая, что угловое ускорение определяется выражением

получим формулу для момента силы, представленного через момент инерции:

Замечание. Момент силы считается положительным, если угловое ускорение, которым он вызван, больше нуля, и наоборот.

Видео:Поступательное и вращательное движенияСкачать



Теорема Штейнера. Закон сложения моментов инерции

Если ось вращения тела через центр масс его не проходит, то относительно этой оси можно найти его момент инерции по теореме Штейнера:
I = I₀ + ma 2 ,

где I₀ — начальный момент инерции тела; m — масса тела; a — расстояние между осями.



Если система, которая совершает обороты округ неподвижной оси, состоит из n тел, то суммарный момент инерции такого типа системы будет равен сумме моментов, ее составляющих (закон сложения моментов инерции).

🎥 Видео

ИЗУЧЕНИЕ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛАСкачать



Поступательное и вращательное движения.Скачать



Момент инерцииСкачать



Консультация к устному экзамену. Механика. Часть 4: "Вращение твердых тел"Скачать



Кинематика: Поступательное и вращательное движение твёрдого тела. Центр онлайн-обучения «Фоксфорд»Скачать