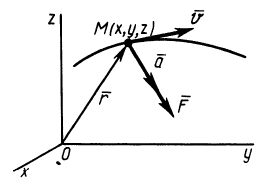
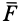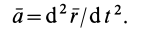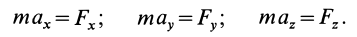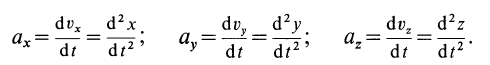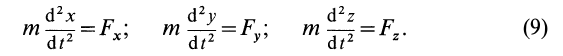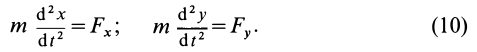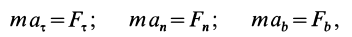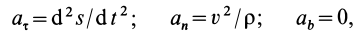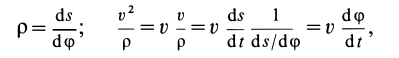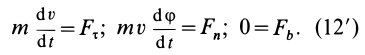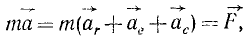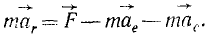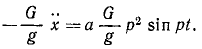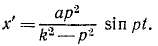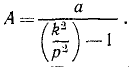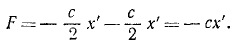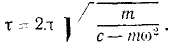Движение материальной точки в пространстве – это изменение ее положения относительно других тел с течением времени.
Имеет смысл говорить только о движении в некоторой системе отсчета.
- Система отсчета. Системы координат
- Кинематическое уравнение движения материальной точки
- Дифференциальные уравнения движения материальной точки в теоретической механике
- Частные случаи дифференциального уравнения движения материальной точки
- Дифференциальные уравнения относительного движения точки
- Пример решения задачи №1
- Пример решения задачи №2
- Пример решения задачи №3
- Траектория и уравнения движения точки
- Траектория и уравнения движения точки
- 📽️ Видео
Видео:Траектория и уравнения движения точки. Задача 1Скачать

Система отсчета. Системы координат
Точки, располагаемые в пустом пространстве, не различаются. Поэтому о точке рассуждают при условии нахождения в ней материальной точки. Определить ее положение можно при помощи измерений в системе координат, где и проводится нахождение пространственных координат. Если рассматривать в виде примера поверхность Земли, то следует учитывать широту и долготу располагаемой точки.
В теории используется декартова прямоугольная система координат, где определение точки возможно при наличии радиус-вектора r и трех проекций x , y , z – ее координат. Могут быть применены другие:
- сферическая система с положением точек и ее радиус-вектором, определенных координатами r , υ , φ ;
- цилиндрическая система с координатами p , z , α ;
- на полярной плоскости с параметрами r , φ .
В теории зачастую не принимают во внимание реальную систему отсчета, а сохраняют только ту, которая представляет собой ее математическую модель, применяемую во время практических измерений.
Видео:Координаты точки и координаты вектора 1.Скачать

Кинематическое уравнение движения материальной точки
Любая система отсчета или координат предполагает определение координат материальной точки в любой момент времени.
При условии положения и определения материальной точки в данной системе отсчета считается, что ее движение задано или описано.
Это возможно при использовании кинематического уравнения движения:
Аналитически положение точки определяется совокупностью трех независимых между собой чисел. Иначе говоря, свободная точка имеет три степени свободы движения.
Ее перемещение по уравнению ( 1 ) определено, если имеется указанное положение в любой момент времени t . Для этого следует задавать декартовы координаты точки в качестве однозначных и непрерывных функций времени:
x ( t ) = x , y ( t ) = y , z ( t ) = z ( 2 ) .
Прямоугольные декартовы координаты x , y , z — это проекции радиус-вектора r ¯ , проведенного из начала координат. Очевидно, что длину и направление r ¯ можно найти из соотношений, где a , β , γ являются образованными радиус-вектором углами с координатными осями.
Равенства ( 2 ) считают кинематическими уравнениями движения материальной точки в декартовых координатах.
Они могут быть записаны в другой системе координат, которая связана с декартовой взаимно однозначным преобразованием. Если движение точки происходит в плоскости О х у , тогда применимы полярные координаты r , φ , относящиеся к декартовым преобразованиям. Данный случай подразумевает использование уравнения движения точки следующего вида:
r = r ( t ) , φ = φ ( t ) ( 3 ) .
Кинематическое уравнение движения точки в криволинейных координатах q 1 , q 2 , q 3 , связанных с декартовыми преобразованиями вида x = x ( q 1 , q 2 , q 3 ) , y = y ( q 1 , q 2 , q 3 ) , z = z ( q 1 , q 2 , q 3 ) ( 4 ) , записывается как
q 1 = q 1 ( t ) , q 2 = q 2 ( t ) , q 3 = q 3 ( t ) ( 5 ) .
Кривая радиус-вектора, описываемая концом вектора r при движении точки, совпадает с ее траекторией. Параметрическое уравнение траектории с t представлено кинематическими уравнениями ( 2 ) , ( 5 ) . Чтобы получить координатное уравнение траектории следует исключить время из кинематических уравнений.
Определение движения точки возможно с помощью задания траектории и мгновенного положения точки на ней. Ее положение на кривой определяется с помощью указания только одной величины: расстояния вдоль кривой от некоторой начальной точки с положительным направлением:
Это и есть уравнение движения точки по траектории. Способ его задания относят к естественному или траекторному.
Понятия координатного и естественного способа задания движения точки физически эквивалентны. С математической стороны это рассматривают как возможность применения разных методов, исходя из случая математической задачи.
Задание такого закона возможно аналитическим, графическим путем или с использованием таблицы, последние два из которых зачастую рассматривают в виде графиков и расписаний движений поездов.
Дано уравнение движения материальной точки x = 0 , 4 t 2 . Произвести запись формулы зависимости υ x ( t ) , построить график зависимости скорости от времени. На графике отметить площадь, численно равную пути, пройденному точкой за 4 секунды, произвести вычисление.
Дано: x = 0 , 4 t 2 , t = 4 c
Найти: υ x ( t ) , S — ?
Решение
При решении необходимо учитывать зависимость скорости от времени:
υ x = υ 0 x + a x t .
Зависимость координаты от времени и сравнение уравнения с заданным принимает вид:
x = x 0 + υ 0 x t + a x t 2 2 , x = 0 , 4 t 2 .
Очевидно, что x 0 = 0 , υ 0 x = 0 , a x = 0 , 8 м / с 2 .
После подстановки данных в уравнение:
Определим точки, изобразим график:
υ x = 0 , t = 0 , υ x = 4 , t = 5
Путь, по которому двигалось тело, равняется площади фигуры, ограниченной графиком, и находится с помощью формулы:
Видео:Как построить точки в системе координат OXYZСкачать

Дифференциальные уравнения движения материальной точки в теоретической механике
Содержание:
Дифференциальные уравнения движения материальной точки:
Используя основной закон динамики, можно вывести дифференциальные уравнения движения материальной точки в различных системах координат. По аксиоме о связях и силах реакций связей можно получить дифференциальные уравнения движения и несвободной точки так же, как и для свободной, только ко всем приложенным к точке силам надо добавить силы реакций связей.
Силы реакций связей при движении точки могут зависеть в общем случае не только от вида наложенных на точку связей и приложенных к ней сил, но и от характера ее движения, например от ее скорости при движении в воздухе или в какой-либо другой сопротивляющейся среде. В дальнейшем не будем делать различия между свободной и несвободной материальными точками. Обозначая равнодействующую всех заданных сил и сил реакций связей
Из кинематики точки известно, что ускорение 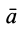
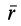
Дифференциальное уравнение движения материальной точки в векторной форме имеет вид
Если спроецировать обе части уравнений (7) или (8) на координатные оси, то можно получить дифференциальные уравнения движения точки в проекциях на эти оси.
В декартовой системе координат в общем случае
Проекции ускорения на координатные оси можно выразить через вторые производные по времени от координат движущейся точки:
Рис. 3
Дифференциальные уравнения движения материальной точки в прямоугольной декартовой системе координат имеют вид
Видео:Скорость и ускорение точки в полярных координатахСкачать

Частные случаи дифференциального уравнения движения материальной точки
Если известно, что материальная точка движется в одной и той же плоскости, то, принимая ее за координатную плоскость 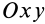
Так как 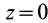
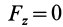
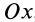
Так как при движении 
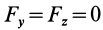
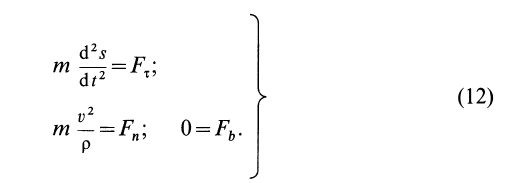
где 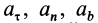
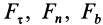
где 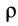
Второе уравнение из (12) можно преобразовать:
где 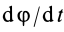
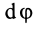
Дифференциальные уравнения (12) можно представить в виде
Рис. 4
Эта форма дифференциальных уравнений движения точки удобна при исследовании некоторых случаев полета снарядов и ракет, особенно по траектории, лежащей в плоскости. Тогда 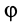
Дифференциальные уравнения движения точки можно представить в любой другой системе координат. Для этого надо знать выражения проекций ускорения на эти оси координат.
Видео:11 класс, 1 урок, Прямоугольная система координат в пространствеСкачать

Дифференциальные уравнения относительного движения точки
Кориолисовыми силами инерции называют две векторные величины, имеющие размерность силы и добавляемые к силам, приложенным к материальной частице, для определения ее относительного ускорения
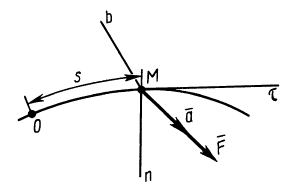
Все дифференциальные уравнения движения, с которыми мы ознакомились в этой главе, относятся к абсолютному движению, т. е. к движению по отношению к инерциальной системе отсчета. Для написания дифференциальных уравнений движения точки (или частицы) относительно подвижных осей подставим в основное уравнение динамики (123) вместо абсолютного ускорения точки его выражение (110):
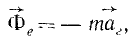
имеющую размерность силы, равную произведению массы материальной частицы на ее переносное ускорение и направленную противоположно этому ускорению, называют переносной силой инерции Кориолиса.
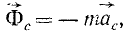
равную произведению массы материальной частицы на ее кориолисово ускорение и направленную противоположно этому ускорению, называют поворотной силой инерции Кориолиса.
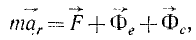
или в проекциях на оси координат:
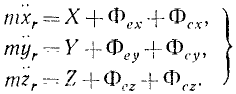
Таким образом, относительное движение материальной точки можно описать такими же (по форме) дифференциальными уравнениями, как и абсолютное, но к действующим на точку силам нужно прибавить две кориолисовы силы инерции: переносную и поворотную.
Эти величины следует отличать от даламберовых сил инерции (см. гл. XX), введение которых позволяет решать задачи динамики методом статики.
Пример решения задачи №1
Определить амплитуду вынужденных колебаний в относительном движении вибрографа для записи вертикальных колебаний фундамента (рис. 171), совершающего вместе с фундаментом колебания по закону χ = a sin pt, если вес груза равен G и жесткость пружины с.
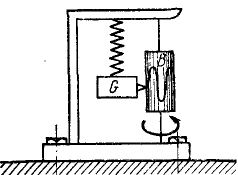
Рис. 171
Решение. Рама жестко соединена с фундаментом и участвует в его колебаниях, как и вращающийся барабан В, на котором груз G, перемещаясь вверх и вниз, записывает колебания фундамента. Вертикальные перемещения х’ груза G по отношению к раме являются относительными и по отношению к барабану, если пренебречь его вращением. Уравнение этих относительных перемещений можно составить как уравнение абсолютного движения, если к заданным силам добавить переносную кориолисову силу, равную и противоположную произведению вектора переносного ускорения на массу груза. Переносная сила инерции груза равна
Напишем дифференциальное уравнение относительных колебаний груза, сократив на m:
x’ + k 2 χ’ = ар 2 sin pt.
где 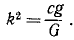
Амплитуда этих колебаний тем менее отличается от амплитуды колебаний фундамента, чем меньше собственная частота k прибора сравнительно с частотой р, т. е. чем меньше жесткость пружины и чем больше масса груза.
Ответ.
Пример решения задачи №2
Ползун G (рис. 172) может скользить по хорде AB равномерно вращающегося горизонтального диска, к точкам А и В которой он прикреплен двумя одинаковыми пружинами жесткостью 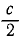
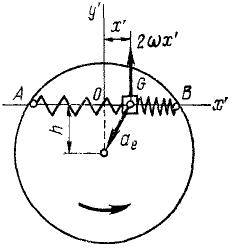
Рис. 172
Решение. Построим оси подвижной системы координат с началом в точке О (в положении относительного равновесия ползуна), направив Ox’ но хорде.
Определим силы, действующие на ползун. Если ползун отклонится от равновесного положения О на величину х’, то одна из пружин сожмется, а другая растянется. Согласно закону Гука сила каждой из пружин пропорциональна деформации х’ и направлена к точке О. Следовательно, на ползун действует активная сила
Кроме активной силы, надо учесть действие кориолисовых сил: Φe—переносной и Φc-поворотной.
Переносная сила инерции равна произведению массы т ползуна на его переносное ускорение: 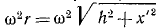
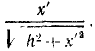
Поворотная сила Кориолиса равна произведению массы ползуна иа кориолисово ускорение 2ωx’ и направлена против этого ускорения. Таким образом, чтобы определить направление поворотной силы Кориолиса, надо вектор относительной скорости повернуть на 90° против переносного вращения. Находим, что поворотная сила инерции действует перпендикулярно AB и проекция ее на Ox’ равна нулю.
При найденных значениях активных сил и кориолисовых сил дифференциальное уравнение относительного движения ползуна по хорде имеет вид:
mх’ = — cx’ + mω 2 x’= — (с—mω 2 )x’.
Это уравнение выражает гармоническое колебание с периодом
Ответ. 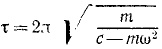
Пример решения задачи №3
Составить дифференциальное уравнение относительного движения ползуна, описанного в предыдущей задаче, считая, что при его движении вдоль хорды AB возникает трение, пропорциональное нормальному давлению на хорду.
Решение. Нормальное давление обусловлено поворотной силой инерции и нормальной составляющей переносной силы инерции.
Поворотная сила ползуна Φс=2mωx’ переменна по величине и направлению. Она направлена перпендикулярно к хорде AB, но в сторону положительных значений у’, если точка G движется в сторону отрицательных значений х’, т. е, если х’ 2 h. Эта составляющая в рассматриваемом механизме всегда направлена в сторону положительных у’, а потому в суммарном давлении обе кориолисовы силы складываются при х’ 0, и дифференциальное уравнение относительного движения точки имеет вид
mх’ =— (с—mω 2 ) x’ — fm (2ωx’ ± ω2h),
причем знак второго слагаемого в скобках надо брать положительным при х’ 0. Решение такого уравнения при движении точки G влево и вправо получается, конечно, различным. Если Л — 0 и хорда является диаметром, то вместо кулонова трения получается вязкое демпфирование, зависящее от скорости.
| Рекомендую подробно изучить предмет: |
|
| Ещё лекции с примерами решения и объяснением: |
- Две основные задачи динамики точки
- Прямолинейное движение точки
- Криволинейное движение материальной точки
- Движение несвободной материальной точки
- Сложное движение точки
- Сложение движение твердого тела
- Кинематика сплошной среды
- Аксиомы классической механики
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Уравнение движенияСкачать

Траектория и уравнения движения точки

















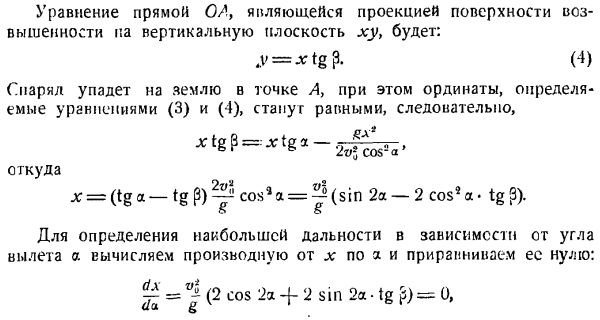











Видео:9 класс. Геометрия. Декартовы координаты. Уравнение окружности. Уравнение прямой. Урок #6Скачать

Траектория и уравнения движения точки
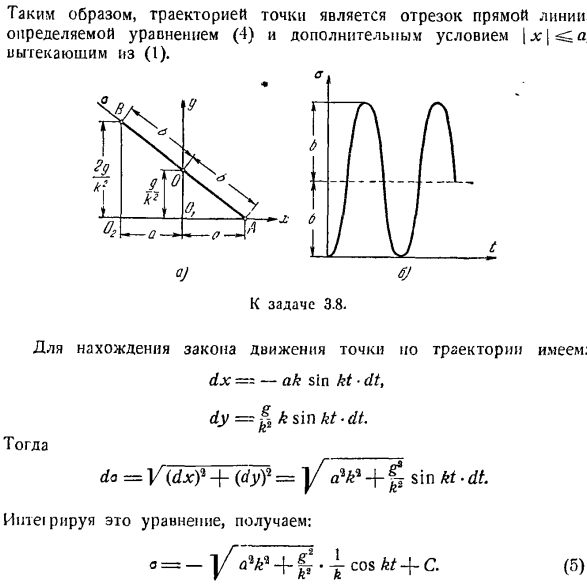
- Уравнение движения для локуса и точек 1°.Основные понятия. Траекторией точки называется линия, описываемая точкой движения в пространстве. Траектории могут быть плоскими или пространственными кривыми. Движение точки определяется установлением закона движения. Закон движения точек (уравнения) устанавливает зависимость расположения точек во временном пространстве.
Движение точки M в фиксированной системе координат xyz определяется установкой 3 функций (рис.3.1). * = / > ( ’). J’ = / *( Людмила Фирмаль
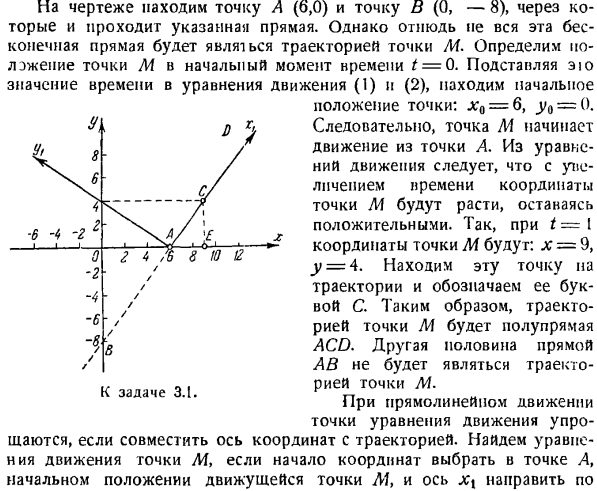
Создайте уравнение движения для точки N в декартовой системе координат. Найдите уравнение его орбиты. Определяет полный 1-кратный поворот точки N и точку, в которой координаты обеих точек равны. The solution. To составьте уравнение движения точки N, необходимо представить ее координаты в виде функции времени. Из рисунка найдите координату x в точке N. Х = О с COS Людмила Фирмаль
Затем по координатам определяется максимальное отклонение точки м от центра колебаний О. МПМ = а ХІ =-а. Величина a называется амплитудой колебаний, kt — (- (J называется фазой колебаний, ap-начальной фазой колебаний. Определите период колебаний, то есть время, в течение которого точки совершают 1 полное колебание, то есть возвращаются в исходное положение с той же скоростью и величиной. Обозначим период буквой Т и найдем его значение из условия, что приращение фазы колебаний за это время равно 2π. Иначе говоря
Задача 3.4.Точки перемещаются в соответствии с уравнением. x = A cos(kt-e), (1) г = Б, потому что КТ(2) Определите уравнение траектории движения точки. Как изменяется локус точек при увеличении разности фаз£от 0 до 2r? The solution. To найдя уравнение орбиты точки в явном виде, нужно исключить время из уравнения motion. To для этого сначала преобразуем уравнение движения. х = а соѕ(т-е)= а [потому что КТ потому что£-(- КТ грех грех ЭЖ.(3) решая уравнения (2) и (3) для cos kt и sin kt, получим: Х г — г соз£ а б. Преступление. потому что КТ =£о грех КТ = Добавьте эти уравнения, возведя их в квадрат. г, (т -£»»’) ’ 1 Б% ’ °1 (4) Sin2 е
Или в конце: — В + М — ^^ ко ^ грех ’、 уравнение (4) для любого значения e является уравнением эллипса. Из этого уравнения максимальные и минимальные значения являются Параметры±соответственно. a для x и zt b для y. таким образом, во всех случаях эллипс вписывается в прямоугольники со сторонами 2a и 2b. измените значение от 0 до 2ir. если e = 0, то выражение(4) принимает вид:
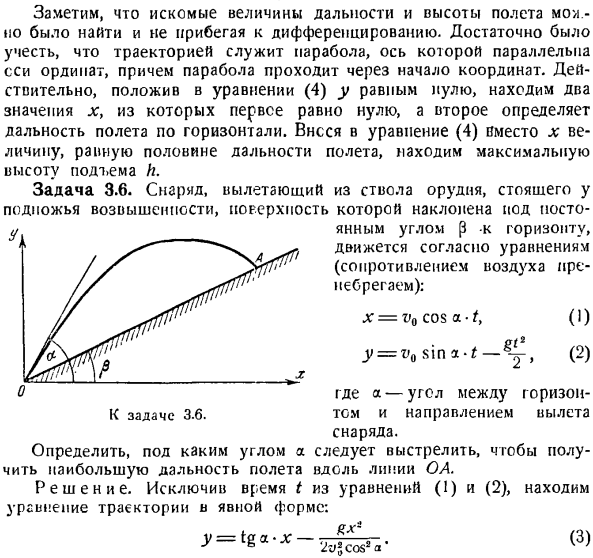
Так, если фазы обеих составляющих колебаний перпендикулярны друг другу, то эллипс вырождается в 2 совпадающие прямые, являющиеся диагоналями прямоугольника(рис. в коса -> -= учитывая it_y = 0, горизонтальная дальность полета I определяется из орбитального уравнения (4).
log A x cos2 a следовательно 2 значения x Т / л грех 2а х0 = 0, ХН = 1 = 8. Первое значение соответствует первому моменту (моменту отправления точки), А второе определяет горизонтальное расстояние. Сравнивая значения /и 5, можно сделать вывод, что/ = 2s, то есть точки достигают наивысшего положения в диапазоне горизонтальной половины. Итак, положение точки в пространстве в этой точке.
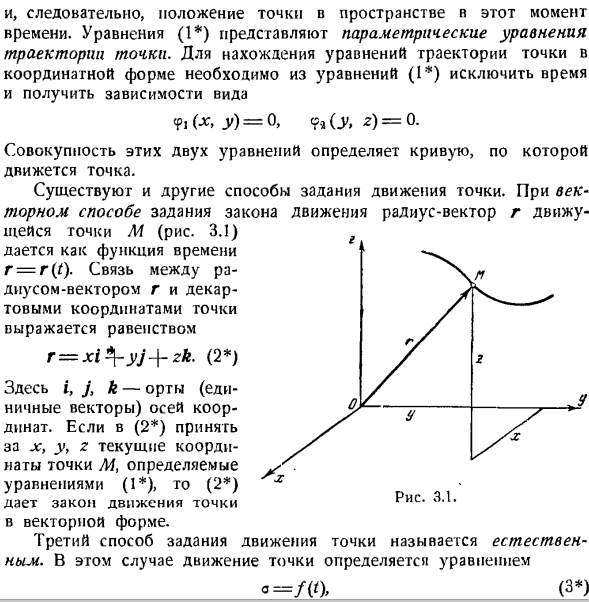
Уравнение (1) представляет собой параметрическое уравнение траектории a point. To найдя уравнение орбиты точки в координатной форме, нужно исключить время из уравнения(1) и получить форму зависимости. БФ,(Ци, г)= 0, 9а, КР, з)= 0. Комбинация этих 2 уравнений определяет кривую, по которой перемещаются точки. Есть и другие способы указать движение points. In векторным методом, определяющим законы движения, радиус-вектор r движущейся точки M (рис.3.1) задается как функция времени r = r (t).Связь между радиус-вектором r и Декартовыми координатами точки представлена уравнением Р = ХІ * — ый + ЗК. (2 ) Где i, j и k-единичные векторы (единичные векторы) осей. (2)
Если вы получаете x, y> z, текущие координаты точки A4, как определено y. уравнение(1), то (2) x Дайте закон движения точек в векторной форме. 3-й способ задания движения точек называется natural. In в этом случае движение точек определяется уравнением а = /( (). Сферические и цилиндрические координаты часто используются для изучения движения точки в пространстве. Сферическими координатами точки M (рис.3.4) являются расстояние r точки M от неподвижного центра O, угол φ (угол поворота плоскости zOM относительно неподвижной плоскости xOz) и угол ? =?(’) * (5 *)
Уравнение движения для цилиндрических координат: р = п(о> т = м р = РЗ). (си *) м г Так… 1. Рисунок 3.4. Да. Чтобы перейти от сферических координат к декартовым, используйте следующую формулу:> х = р с с COS




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
📽️ Видео
Дифференциальные уравнения движения точкиСкачать

Полярная система координатСкачать

7.9. Задание движения точки в полярных координатахСкачать

Прямоугольная система координат в пространстве. 11 класс.Скачать

Геометрия 11 класс (Урок№1 - Координаты в пространстве. Система координат.)Скачать

Видеоурок "Преобразование координат"Скачать

Урок 7. Механическое движение. Основные определения кинематики.Скачать

Дифференциальные уравнения движения материальной точкиСкачать
ДЕКАРТОВЫ КООРДИНАТЫ. Контрольная № 3 Геометрия 9 класс.Скачать

Координаты на плоскости и в пространстве. Вебинар | МатематикаСкачать

Движение точки тела. Способы описания движения | Физика 10 класс #2 | ИнфоурокСкачать

§56 Сферическая система координатСкачать

Декартовые координаты на плоскости. Алгеба 8 класс. Урок 1Скачать