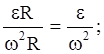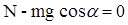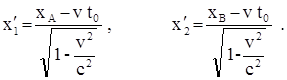Читайте также:
|
| x = A + Bt + Ct 3 A = 4 м B = 2 м/c C = 0,2 м/c 3 t1 = 2 c; t2 = 5 c | Решение 1. Чтобы найти координаты точки, надо в уравнение движения подставить значения t1 и t2: x1 = (4+2×2+0,2×2 3 ) м = 9,6 м, x2 = (4+2×5+0,2×5 3 ) м = 39 м. |
| x1, x2, — ? u1, u2 — ? , a1, a2 — ? | 2. Средняя скорость  , , |

3. Мгновенные скорости найдем, продифференцировав по времени уравнение движения:
u1 = (2+3×0,2×2 2 ) м/с = 4,4 м/c;
u2 = (2+3×0,2×5 2 ) м/с = 17 м/с.
4. Среднее ускорение 
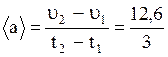
5. Мгновенное ускорение получим, если продифференцируем по времени выражение для скорости: a = 2×3×Ct = 6Ct.
a1 = 6×0,2×2 м/c 2 = 2,4 м/с 2 ;
a2 = 6×0,2×5 м/с 2 = 6 м/с 2 .
Ответ: x1 = 9,6 м; x2 = 39 м; áuñ = 9,8 м/с; u1 = 4,4 м/c; u2 = 17 м/с; áаñ = 4,2 м/с 2 ; a1 = 2,4 м/с 2 ; a2 = 6 м/с 2 .
Задача 2 Маховик вращается равноускоренно. Найти угол a, который составляет вектор полного ускорения 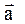
| w0 = 0 N = 2 e = const | Решение Разложив вектор  точки М на тангенциальное точки М на тангенциальное  и нормальное и нормальное  ускорения, видим, что искомый угол определяется соотношением tga=at/an. ускорения, видим, что искомый угол определяется соотношением tga=at/an. |
| a — ? |
Поскольку в условии дано лишь число оборотов, перейдем к угловым величинам. Применив формулы: at = eR, an = w 2 R, где R – радиус маховика, получим
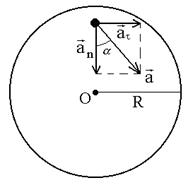
так как маховик вращается равноускоренно, найдем связь между величинами e и w;
Поскольку w0 = 0; j = 2pN, то w 2 = 2e×2pN = 4pNe.
Подставим это значение в формулу, получим:
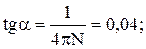
Задача 3 Две гири с массами m1 = 2 кг и m2 = 1 кг соединены нитью, перекинутой через невесомый блок. Найти ускорение a, с которым движутся гири, и силу натяжения нити 
| m1 = 2 кг m2 = 1 кг | Решение Воспользуемся для решения задачи основным законом динамики  где где  – равнодействующая всех сил, действующих на тело. – равнодействующая всех сил, действующих на тело. |
| a, FН — ? |
На тело 1 и тело 2 действуют только две силы – сила тяжести и сила
натяжения нити. Для первого тела имеем

 |
для второго тела

Так как сила трения в блоке отсутствует,

Ускорения тел а1 и а2 направлены в противоположные стороны и равны по модулю:

Получаем из выражений (1) и (2) систему уравнений
Выберем ось Х, как показано на рисунке и запишем полученную систему уравнений
в проекции на ось Х
Решая эту систему относительно а и FН, получаем:


Ответ: a= 3,3 м/c 2 ; FH = 13 Н.
Задача 4 К ободу однородного диска радиусом R=0,2 м приложена касательная сила F=98,1 Н. При вращении на диск действует момент сил трения
МТР=4,9 Н×м. Найти массу m диска, если известно, что диск вращается с угловым ускорением e=100 рад/с 2 .
| R = 0,2 м F = 98,1 Н MТР = 4,9 Н×м e = 100 рад / c 2 | Решение Воспользуемся основным законом динамики вращательного движения, записанным для оси вращения, направление которой совпадает с направлением угловой скорости:  , где , где  — момент сил, приложенных к телу, — момент сил, приложенных к телу, |
| m — ? |
относительно выбранной оси ( MF — момент силы F, Mтр – момент сил трения);

Учитывая, что MF=F×R, получаем 
Отсюда 
Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.007 сек.)
Видео:Уравнение движенияСкачать

Примеры решения задач по теме №1
«Механика и элементы специальной теории относительности»
Задача 1 Уравнение движения точки по прямой имеет вид: x = A+Bt+Ct 3 , где А = 4 м, В = 2 м/c, С = 0,2 м/с 3 . Найти: 1) положение точки в моменты времени t = 2 c и t = 5 с; 2) среднюю скорость за время, протекшее между этими моментами; 3) мгновенные скорости в указанные моменты времени; 4) среднее ускорение за указанный промежуток времени; 5) мгновенные ускорения в указанные моменты времени.
| x = A + Bt + Ct 3 A = 4 м B = 2 м/c C = 0,2 м/c 3 t1 = 2 c; t2 = 5 c | Решение 1. Чтобы найти координаты точки, надо в уравнение движения подставить значения t1 и t2: x1 = (4+2×2+0,2×2 3 ) м = 9,6 м, x2 = (4+2×5+0,2×5 3 ) м = 39 м. |
| x1, x2, — ? u1, u2 — ? , a1, a2 — ? | 2. Средняя скорость  , , |

3. Мгновенные скорости найдем, продифференцировав по времени уравнение движения:
u1 = (2+3×0,2×2 2 ) м/с = 4,4 м/c;
u2 = (2+3×0,2×5 2 ) м/с = 17 м/с.
4. Среднее ускорение 
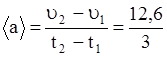
5. Мгновенное ускорение получим, если продифференцируем по времени выражение для скорости: a = 2×3×Ct = 6Ct.
a1 = 6×0,2×2 м/c 2 = 2,4 м/с 2 ;
a2 = 6×0,2×5 м/с 2 = 6 м/с 2 .
Ответ: x1 = 9,6 м; x2 = 39 м; áuñ = 9,8 м/с; u1 = 4,4 м/c; u2 = 17 м/с; áаñ = 4,2 м/с 2 ; a1 = 2,4 м/с 2 ; a2 = 6 м/с 2 .
Задача 2 Маховик вращается равноускоренно. Найти угол a, который составляет вектор полного ускорения 
| w0 = 0 N = 2 e = const | Решение Разложив вектор  точки М на тангенциальное точки М на тангенциальное  и нормальное и нормальное  ускорения, видим, что искомый угол определяется соотношением tga=at/an. ускорения, видим, что искомый угол определяется соотношением tga=at/an. |
| a — ? |
Поскольку в условии дано лишь число оборотов, перейдем к угловым величинам. Применив формулы: at = eR, an = w 2 R, где R – радиус маховика, получим
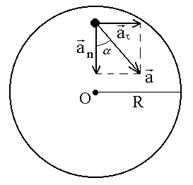
так как маховик вращается равноускоренно, найдем связь между величинами e и w;
Поскольку w0 = 0; j = 2pN, то w 2 = 2e×2pN = 4pNe.
Подставим это значение в формулу, получим:

Задача 3 Две гири с массами m1 = 2 кг и m2 = 1 кг соединены нитью, перекинутой через невесомый блок. Найти ускорение a, с которым движутся гири, и силу натяжения нити 
| m1 = 2 кг m2 = 1 кг | Решение Воспользуемся для решения задачи основным законом динамики  где где  – равнодействующая всех сил, действующих на тело. – равнодействующая всех сил, действующих на тело. |
| a, FН — ? |
На тело 1 и тело 2 действуют только две силы – сила тяжести и сила
натяжения нити. Для первого тела имеем

 |
для второго тела

Так как сила трения в блоке отсутствует,

Ускорения тел а1 и а2 направлены в противоположные стороны и равны по модулю:

Получаем из выражений (1) и (2) систему уравнений
Выберем ось Х, как показано на рисунке и запишем полученную систему уравнений
в проекции на ось Х
Решая эту систему относительно а и FН, получаем:


Ответ: a= 3,3 м/c 2 ; FH = 13 Н.
Задача 4 К ободу однородного диска радиусом R=0,2 м приложена касательная сила F=98,1 Н. При вращении на диск действует момент сил трения
МТР=4,9 Н×м. Найти массу m диска, если известно, что диск вращается с угловым ускорением e=100 рад/с 2 .
| R = 0,2 м F = 98,1 Н MТР = 4,9 Н×м e = 100 рад / c 2 | Решение Воспользуемся основным законом динамики вращательного движения, записанным для оси вращения, направление которой совпадает с направлением угловой скорости:  , где , где  — момент сил, приложенных к телу, — момент сил, приложенных к телу, |
| m — ? |
относительно выбранной оси ( MF — момент силы F, Mтр – момент сил трения);

Учитывая, что MF=F×R, получаем 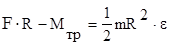
Отсюда 
Задача 5 На гладкой горизонтальной поверхности находятся две одинаковые соприкасающиеся шайбы. Третья такая же шайба налетает на них со скоростью v0 = 6 м/с, направленной по общей касательной к неподвижным шайбам. После столкновения налетевшая шайба движется вдоль первоначального направления со скоростью v1 = 2 м/с. Найти величину энергии, перешедшей во внутреннюю энергию тел при столкновении. Масса каждой шайбы m = 100 г.



Поскольку размеры всех шайб одинаковы, то скорости v2 и v3, направленные вдоль прямых,
соединяющих центры шайб в момент удара, составляют одинаковые углы a = 30 о с осью X, а так как массы всех шайб по условию равны, то очевидно, что скорости v2 и v3 равны по модулю, то есть v2 = v3 = v.
Теперь запишем закон сохранения импульса для проекций импульсов взаимодействующих тел на ось X:
Тогда mv0 = mv1 + 2 mv сosa.
Отсюда 
Энергию, перешедшую во внутреннюю энергию тел при частично неупругом ударе, можно найти как разность кинетической энергии налетающей шайбы до удара и суммарной кинетической энергии всех тел после удара:

Ответ: DU = 1,07 Дж.
Задача 6 Небольшое тело массой m равномерно втащили на горку, действуя силой, которая в каждой точке направлена по касательной к траектории. Найти работу этой силы, если высота горки h, длина ее основания l, и коэффициент трения m.

Работу, совершаемую силой 

Для этого необходимо предварительно найти силу 




Выберем координатные оси х и у таким образом, чтобы ось х была направлена по касательной к траектории (вдоль перемещения 
Запишем векторное равенство в проекциях на эти координатные оси:
oсь x:
oсь y:
Тогда 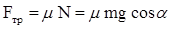

Теперь можно найти выражение для элементарной работы, совершаемой силой F при перемещении тела на расстояние dr. При этом учтем, что угол между векторами 

Тогда 
Из рис. видно, что 

Тогда 
и полная работа, совершаемая силой F при втаскивании тела на горку:


Ответ: 
Задача 7 Круглая платформа радиусом R=1,0 м, момент инерции которой J=130 кг×м 2 , вращается по инерции вокруг вертикальной оси, делая n1=1,0 об/с. На краю платформы стоит человек, масса которого m=70 кг. Сколько оборотов в секунду n2 будет совершать платформа, если человек перейдет в её центр? Момент инерции человека рассчитывать как для материальной точки.
| R = 1м J = 130 кг × м 2 n1 = 1c -1 m = 70 кг | Решение Согласно условию задачи, платформа с человеком вращается по инерции. Это означает, что результирующий момент всех внешних сил, приложенных к вращающейся системе, равен нулю. Следовательно, для системы “платформа + человек” выполняется закон сохранения момента импульса, который запишем в скалярной форме относительно оси, совпадающей с осью вращения и направленной по угловой скорости: |
| n2 — ? |
где L1 — импульс системы «платформа + человек на краю платформы», L2 — импульс системы «платформа + человек в центре платформы».
где mR 2 — момент инерции человека, J1 = J+mR 2 — момент инерции системы «платформа + человек на краю платформы», J2 — момент инерции системы «платформа + человек в центре платформы», w1 и w2 — соответствующие угловые скорости системы. Решая систему уравнений (1) — (3), получаем
Задача 8 В условно неподвижной системе отсчета К в точках с координатами xA и xB = xA + l, где l = 1 км, одновременно происходят два события A и B. На каком расстоянии l¢АВ друг от друга зафиксирует эти события наблюдатель в системе К¢, движущейся со скоростью v = 0,4×с вдоль оси X? Какой промежуток времени Dt¢ между этими событиями зафиксирует наблюдатель в системе К¢?

Обозначим через t0 момент времени, когда в системе К происходят события А и В. Тогда событие А в этой системе обладает пространственно – временными координатами xA и t0, а событие В – координатами xB и t0. В системе К¢ событие А обладает пространственно–временными координатами x1¢ и t1¢, а событие В – координатами x2¢ и t2¢. Связь координат каждого из событий можно записать с помощью преобразований Лоренца.
Найдя разность этих выражений, получим расстояние между точками, в которых происходят события А и В в системе К¢.
Видно, что расстояние l¢АВ, разделяющее события А и В в любой системе, движущейся относительно К, больше, чем это же расстояние, измеренное в системе К, в которой оба события одновременны. Рассчитаем расстояние l¢АВ.
Моменты времени, в которые в системе К¢ наблюдатель зафиксирует события А и В, также могут быть найдены из преобразований Лоренца:
Видно, что события А и В в системе отсчета К¢ не являются одновременными. Если xB > xA и система К¢ движется в положительном направлении оси X, как и задано в условии, то t2¢ — t1¢ .
Видео:Траектория и уравнения движения точки. Задача 1Скачать

Уравнение движения точки по прямой имеет вид x a bt ct3
Кинематическое уравнение движения материальной точки по прямой (ось х) имеет вид x=A+Bt+Ct 3 , где А=4 м, В= =2 м/с, С=—0,5 м/с 2 . Для момента времени t1=2 с определить: 1) координату X1 точки, 2) мгновенную скорость v1 3) мгновенное ускорение а1

Автомобиль движется по закруглению шоссе, имеющему радиус кривизны R=50 м. Уравнение * движения автомобиля ξ(t)=A+Bt+Ct 2 , где A= 10 м, B=10 м/с, С=—0,5 м/с 2 . Найти 1) скорость v автомобиля, его тангенциальное аt нормальное ап и полное а ускорения в момент времени t=5 с; 2) длину пути s и мо дуль перемещения автомобиля за интервал времени t=10 с, отсчитанный с момента начала движения.
Маховик, вращавшийся с постоянной частотой n0=10 с -1 , при торможении начал вращаться равнозамедленно. Когда торможение прекратилось, вращение маховика снова стало равномерным, но уже с частотой n=6 с -1 . Определить угловое ускорение ε маховика и продолжительность t торможения, если за время равнозамедленного движения маховик сделал N=50 оборотов.
Пример 1. Уравнение движения математической точки вдоль оси Х имеет вид х = А + Вt + Ct 2 , где А = 4 м, В = 2 м/с, С = 0,5 м/с 2 . Найти координату х1, скорость v1 и ускорение а 1 в момент времени t1 = 2 с.
Решение. Координату х1 найдем, подставив в уравнение движения числовые значения коэффициентов А, В, С и времени t1 = 2 с:
х1 = (4 + 2 · 2 — 0,5 · 2 2 ) м = 6 м.
Мгновенная скорость равна первой производной от координаты по времени:

Ускорение точки найдем, как первую производную от скорости по времени:

В момент времени t1 = 2 с:
v1 = (2 – 2 · 0,5 · 2) м/ с = 0 м/с, а1 = 2 (0,5) = – 1 м/с 2 .
Знак минус указывает на то, что направление вектора ускорения совпадает с отрицательным направлением координатной оси.
Размерности искомых величин очевидны.
Материальная точка движется в плоскости согласно уравнениям х = А1+ B1t + С1t 2 и у = А2 +B2t + С2t 2 , где В1= 7 м/с, С1= -2 м/с 2 , В2= -1 м/с,С2= 0,2 м/с 2 , Найти модули скорости v и ускорения а точки в момент времени t= 5 с.
Задача 1. Материальная точка движется по следующему закону 


Физическая система состоит из одного идеального объекта материальной точки. Задан формально закон ее движения. Следовательно, наша задача прямая задача кинематики: по известному закону движения определить один или несколько параметров движения. Находим компоненты радиус-вектора:



Таким образом, движение материальной точки происходит в плоскости XOY. Далее определяем компоненты вектора скорости:


Находим компоненты вектора ускорения:


С учетом численных значений 



Для получения уравнения траектории исключим время t из системы уравнений (1). Тогда получим уравнение кривой, по которой движется материальная точка:

Итак, траекторией движения материальной точки является парабола.
Уравнение движения точки r = (4+3t)i + j(5-4t). Найти скорость и ускорение точки, ее траекторию.
Пример 2. Камень брошен под углом = 45 к горизонту. Определить наибольшую высоту подъема и дальность полета, если начальная скорость камня v0 = 20 м/с.
Решение. Пренебрегая сопротивлением воздуха, можно считать, что ускорение камня в рассматриваемом движении постоянно и равно ускорению свободного падения 


В точке бросания составляющие скорости равны:
В произвольный момент времени t, скорости движение камня
В наивысшей точке траектории (в момент времени t1) vy1 = 0, тогда
v0 sin – gt1 = 0 , t1 =
Наибольшую высоту подъема найдем из уравнения движения камня по

Время подъема камня на наибольшую его высоту равно времени падения на землю.
Тогда полное время полета

Наибольшая дальность полета

Подставив числовые значения, получим


Анализ размерности искомых величин:

Камень брошен с некоторой высоты горизонтально со скоростью v0 = 10 м/с. Найти радиус кривизны R траектории кам ня через t= 3 с после начала движения, а также значения нормального аt и тангенциального аn ускорений в этот момент времени. Ускорение свободного падения g = 10 м/с 2 .
К старости недостатки ума становятся все заметнее, как и недостатки внешности. Франсуа Ларошфуко
ещё >>
Видео:Уравнение движения тела дано в виде x=2−3t. ВычислиСкачать

Примеры решения задач. 1. Частица движется вдоль прямой по закону x=A+Bt+Ct3 , где А=3 м, В=2,5 м/с, С=0,25м/c3
1. Частица движется вдоль прямой по закону x=A+Bt+Ct 3 , где А=3 м, В=2,5 м/с, С=0,25м/c 3 . Найти средние значения скорости и ускорения за интервал времени от t1=1 с до t2=6 с.
| Дано: | Решение: |
| x=A+Bt+Ct 3 А=3 м В=2,5 м/с С=0,25м/c 3 t1=1 с t2=6 с | Средняя скорость это отношение перемещения к промежутку времени, за которое это перемещение произошло, тогда модуль средней скорости равен: 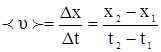 , где , где  =3+2,5×1+0,25×1 3 =5,75 м =3+2,5×1+0,25×1 3 =5,75 м |
| Найти: — ? — ? | 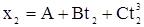 =3+2,5×6+0,25×6 3 =72 м Средняя скорость: =3+2,5×6+0,25×6 3 =72 м Средняя скорость:  |
Среднее ускорение это отношение изменения скорости к промежутку времени, за который это изменение произошло, тогда модуль среднего ускорения равен:  , где , где    Среднее ускорение: Среднее ускорение:  Ответ: Ответ:  ; ; 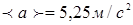 . . |
2. Тело вращается вокруг неподвижной оси по закону 
| Дано: | Решение: |
 r=0,1 м t=4 с r=0,1 м t=4 с | Угловая скорость w вращающегося тела равна первой производной от угла поворота от времени: 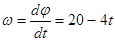 |
| Найти:а — ? | В момент времени t=4 с: w=20-4×4=4 рад/с |
 | Угловое ускорение e вращающегося тела равно первой производной от угловой скорости по времени:  рад/с 2 Материальная точка, принадлежащая телу, движется по окружности радиуса r. Движение материальной точки ускоренное с постоянным угловым ускорением (e=const). Следовательно, тангенциальное ускорение аt будет посто- янным, а нормальное ускорение аn непрерывно возрастаетсо временем, т.е. вектор полного ускорения точки со временем изменяется как по модулю, так и по направлению. Полное ускорение точки, движущейся по окружности, может быть найдено как геометрическая сумма тангенциального ускорения рад/с 2 Материальная точка, принадлежащая телу, движется по окружности радиуса r. Движение материальной точки ускоренное с постоянным угловым ускорением (e=const). Следовательно, тангенциальное ускорение аt будет посто- янным, а нормальное ускорение аn непрерывно возрастаетсо временем, т.е. вектор полного ускорения точки со временем изменяется как по модулю, так и по направлению. Полное ускорение точки, движущейся по окружности, может быть найдено как геометрическая сумма тангенциального ускорения  , направленного по касательной к траектории и нормального ускорения , направленного по касательной к траектории и нормального ускорения  , направленного к центру кривизны траектории. Модуль полного ускорения: , направленного к центру кривизны траектории. Модуль полного ускорения:  (1) (1) |
Тангенциальное ускорение точки вращающегося тела выражается формулой: аt=e×r, (2) где e — угловое ускорение тела. Нормальное ускорение точки вращающегося тела выражается формулой: аn=w 2 r, (3) где w — угловая скорость тела. Подставив выражения (2) и (3) в формулу (1), получаем  (4) (4) | |
Подставив найденные значения w и e и заданное значение r в формулу (4), получим:  м/с 2 Направление полного ускорения определится, если найти угол, который вектор ускорения образует с нормалью к траектории (см. рис.): м/с 2 Направление полного ускорения определится, если найти угол, который вектор ускорения образует с нормалью к траектории (см. рис.):  или или  (5) По формулам (2) и (3) найдем значения (5) По формулам (2) и (3) найдем значения  и и 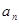 : :  =-0,4 м/с 2 , =-0,4 м/с 2 , 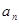 =1,6 м/с 2 . Подставив эти значения и значение полного ускорения в формулы (5), получим: cosa=0,97, sina=0,24. =1,6 м/с 2 . Подставив эти значения и значение полного ускорения в формулы (5), получим: cosa=0,97, sina=0,24. | |
| Пользуясь тригонометрическими таблицами или калькулятором, найдем значение угла a: a»14°. Ответ: a=1,65 м/с 2 , a»14°. |
3. Автомашина массой m=1,8 т движется в гору, уклон которой составляет 3 м на каждые 100 м пути, и за 5 мин преодолевает путь S=5 км. Определить: 1) работу, совершаемую двигателем автомашины, если коэффициент трения равен 0,1; 2) развиваемую двигателем мощность.
| Дано: | Решение: |
| m=1,8 т=1800 кг h=3 м l=100 м t=5 мин=300 с S=5 км=5000 м m=0,1 |  Сделаем рисунок. Покажем, какие силы действуют на автомашину. Сделаем рисунок. Покажем, какие силы действуют на автомашину. |
| Найти: A-? P-? | Уравнение движения автомашины в векторной форме:  |
Запишем это уравнение в проекциях на оси x и y (см. рис.): ox:  oy: oy:  Из последнего Из последнего  , тогда , тогда 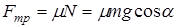 . Сила тяги двигателя автомашины будет равна: . Сила тяги двигателя автомашины будет равна:  Работа, совершаемая двигателем автомашины: Работа, совершаемая двигателем автомашины:  , где , где  , ,  , ,  Подставляем числовые значения и получаем: Подставляем числовые значения и получаем:  = =12,7 МДж Средняя мощность, развиваемая двигателем автомашины: = =12,7 МДж Средняя мощность, развиваемая двигателем автомашины:  кВт кВт | |
Максимальная мощность, развиваемая двигателем автомашины:  , где , где  Подставляем числовые значения и получаем: Подставляем числовые значения и получаем:  84 кВт Ответ: A=12,7 МДж; áPñ=42 кВт; Pmax=84 кВт. 84 кВт Ответ: A=12,7 МДж; áPñ=42 кВт; Pmax=84 кВт. |
4. Шар массой m1=3 кг движется со скоростью u1=2 м/с и сталкивается с покоящимся шаром массой m2=5 кг. Какая работа будет совершена при деформации шаров? Удар считать абсолютно неупругим, прямым, центральным.
| Дано: | Решение: |
| m1=3 кг u1=2 м/с m2=5 кг | Работа будет равна изменению кинетической энергии системы: 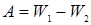 , (1) , (1) |
| Найти: A — ? | где кинетическая энергия шаров до столкновения:  (2) (2) |
Она равна кинетической энергии первого шара, т.к. второй шар покоится. 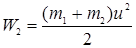 (3) кинетическая энергия шаров после столкновения. Здесь скорость u – скорость системы двух шаров после столкновения. Для ее определения воспользуемся законом сохранения импульса: (3) кинетическая энергия шаров после столкновения. Здесь скорость u – скорость системы двух шаров после столкновения. Для ее определения воспользуемся законом сохранения импульса:   (4) Из выражений (1) – (4) окончательно получаем: (4) Из выражений (1) – (4) окончательно получаем:  Подставляем числовые значения и получаем: Подставляем числовые значения и получаем:  Дж Ответ: А=3,74 Дж Дж Ответ: А=3,74 Дж |
5. Камень брошен со скоростью u0=15 м/с под углом a=60° к горизонту. Найти кинетическую, потенциальную и полную энергии камня: а) через 1 с после начала движения; б) в высшей точке траектории. Масса камня m=0,2 кг.
| Дано: | Решение: |
| u0=15 м/с a=60° t=1 с m=0,2 кг | Движение камня сложное, криволинейное: вдоль оси OX равномерное с постоянной скоростью  , (1) а вдоль оси OY равнопеременное с постоянным ускорением g=9,8 м/с 2 :. , (1) а вдоль оси OY равнопеременное с постоянным ускорением g=9,8 м/с 2 :. |
| Найти: Wк — ? Wп — ? W — ? | 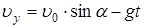 (2) (2) |
 | |
Через t=1 с скорость камня будет равна:  (3) (3) | |
Кинетическая энергия камня через t=1 с будет равна:  Найдем на какой высоте окажется камень через t=1 с: Найдем на какой высоте окажется камень через t=1 с:  Тогда потенциальная энергия камня в этот момент равна: Тогда потенциальная энергия камня в этот момент равна:  Полная механическая энергия камня через t=1 с равна: Полная механическая энергия камня через t=1 с равна:  В верхней точке траектории В верхней точке траектории  , следовательно, полная скорость в этой точке равна: , следовательно, полная скорость в этой точке равна:  . Тогда кинетическая энергия в верхней точке траектории равна: . Тогда кинетическая энергия в верхней точке траектории равна: 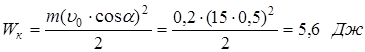 Чтобы найти потенциальную энергию в верхней точке траектории, найдем максимальную высоту подъема. Чтобы найти потенциальную энергию в верхней точке траектории, найдем максимальную высоту подъема. | |
Для этого найдем время подъема. В верхней точке траектории  , следовательно, , следовательно,  Отсюда получаем время подъема: Отсюда получаем время подъема:  Зная время подъема, можно найти максимальную высоту подъема: Зная время подъема, можно найти максимальную высоту подъема:  Найдем потенциальную энергию в верхней точке траектории: Найдем потенциальную энергию в верхней точке траектории: | |
 Полная механическая энергия камня в верхней точке траектории равна: Полная механическая энергия камня в верхней точке траектории равна:  Видно, что выполняется закон сохранения механической энергии: полная механическая энергия камня в верхней точке траектории равна полной механической энергии камня через 1 с после начала полета. Ответ: Wк=5,6 Дж; Wп=16,9 Дж; W=22,5 Дж. Видно, что выполняется закон сохранения механической энергии: полная механическая энергия камня в верхней точке траектории равна полной механической энергии камня через 1 с после начала полета. Ответ: Wк=5,6 Дж; Wп=16,9 Дж; W=22,5 Дж. |
6. Две гири с массами m1=2 кг и m2=1 кг соединены нитью, перекинутой через блок массой m=1 кг. Найти ускорение, с которым движутся гири, и силы натяжения нитей, к которым подвешены гири. Блок считать однородным диском. Трением пренебречь.
| Дано: | Решение: |
| m1=2 кг m2=1 кг m=1 кг | Запишим уравнения движения гирь:  |
| Найти: a — ? Т1 — ? Т2 — ? |  |
 | Запишим эти уравнения в проекциях на ось Y:  (1) (1)  (2) Нить будет натянута по обе стороны блока по-разному, и разность сил натяжения будет создавать момент сил, вращающий блок. Запишим основной закон динамики: (2) Нить будет натянута по обе стороны блока по-разному, и разность сил натяжения будет создавать момент сил, вращающий блок. Запишим основной закон динамики:  , (3) , (3) |
где  , а , а  — момент инерции блока. Решая (1) — (3) совместно, найдем — момент инерции блока. Решая (1) — (3) совместно, найдем  м/с 2 (4) м/с 2 (4) | |
Подставляя (4) в (1) и (2), получим  =14 Н =14 Н  =12,6 Н Ответ: a=2,8 м/с 2 ; T1=14 Н; T2=12,6 Н. =12,6 Н Ответ: a=2,8 м/с 2 ; T1=14 Н; T2=12,6 Н. |
7. Платформа в виде диска радиусом R=1,5 м и массой m1=180 кг вращается по инерции вокруг вертикальной оси, делая n=1/6 с -1 . В центре платформы стоит человек массой m2=60 кг. Какую линейную скорость относительно пола помещения будет иметь человек, если он перейдет на край платформы?
| Дано: | Решение: |
| R=1,5 м m1=180 кг n=1/6 с -1 m2=60 кг | По закону сохранения момента импульса:  , (1) где Jпл, Jчел – моменты инерции платформы и стоящего в ее центре человека; w1 – угловая скорость платформы с , (1) где Jпл, Jчел – моменты инерции платформы и стоящего в ее центре человека; w1 – угловая скорость платформы с |
| Найти: u — ? | человеком, стоящим в ее центре;  — момент инерции человека, стоящего на краю платформы; w2 – угловая скорость платформы с человеком, стоящим на ее краю. Линейная скорость человека, стоящего на краю платформы, связана с угловой скоростью соотношением: u=w2R (2) Определив из уравнения (1) w2 и подставив полученное выражение в (2), будем иметь: — момент инерции человека, стоящего на краю платформы; w2 – угловая скорость платформы с человеком, стоящим на ее краю. Линейная скорость человека, стоящего на краю платформы, связана с угловой скоростью соотношением: u=w2R (2) Определив из уравнения (1) w2 и подставив полученное выражение в (2), будем иметь:  (3) (3) |
Момент инерции платформы определим как для диска:  Момент инерции человека рассчитываем как для материальной точки: Момент инерции человека рассчитываем как для материальной точки:  , ,  | |
Угловая скорость платформы до перехода человека из центра на край платформы: w=2pn. Заменив в формуле (3) величины Jпл, Jчел,  , и w2 их выражениями, получим: , и w2 их выражениями, получим: | |
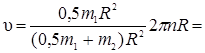  Подставляем числовые значения и получаем: Подставляем числовые значения и получаем: 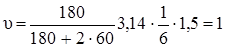 м/с Ответ: u=1 м/с. м/с Ответ: u=1 м/с. |
8. К пружине подвешен груз массой m=10 кг, который совершает колебания с амплитудой 5 см. Зная, что пружина под влиянием силы F=9,8 Н растягивается на l=1,5 см, найти: частоту, период и циклическую частоту вертикальных колебаний пружины, жесткость пружины, полную энергию, максимальную скорость и максимальное ускорение.
| Дано: | Решение: |
| m=10 кг А=5 см=0,05 м F=9,8 Н l=1,5 см=0,015 м | Уравнение гармонических колебаний пружинного маятника имеет вид:  , (1) где s – смещение маятника от положения равновесия; , (1) где s – смещение маятника от положения равновесия; |
| Найти: n — ? T — ? w — ? k — ? W — ? umax — ? amax — ? | А – амплитуда колебаний; w=2pn – циклическая частота;  — частота колебаний; Т – период колебаний; j0 – начальная фаза. — частота колебаний; Т – период колебаний; j0 – начальная фаза. |
Из закона Гука F=kl найдем коэффициент жесткости пружины: 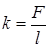 ; ;  653 Н/м Зная коэффициент жесткости пружины, найдем период колебаний груза на пружине: 653 Н/м Зная коэффициент жесткости пружины, найдем период колебаний груза на пружине:  ; ;  с Следовательно, частота и циклическая частота соответст венно равны: с Следовательно, частота и циклическая частота соответст венно равны: | |
 ; ;  Гц; w=2pn=2×3,14×1,25=7,85 с -1 Гц; w=2pn=2×3,14×1,25=7,85 с -1 | |
Скорость колебаний:  , (2) где umax=Аw — максимальная скорость колебаний. umax=0,05×7,85=0,4 м/с Ускорение маятника: , (2) где umax=Аw — максимальная скорость колебаний. umax=0,05×7,85=0,4 м/с Ускорение маятника:  , (3) где , (3) где  — максимальное ускорение. — максимальное ускорение.  м/с 2 Полная энергия маятника: м/с 2 Полная энергия маятника:   Дж Ответ: k=653 Н/м; Дж Ответ: k=653 Н/м;  Гц; Т=0,8 с; w=7,85 с -1 ; umax=0,4 м/с; Гц; Т=0,8 с; w=7,85 с -1 ; umax=0,4 м/с; 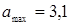 м/с 2 ; W=0,77 Дж. м/с 2 ; W=0,77 Дж. |
9. Волна распространяется в упругой среде со скоростью 150 м/с. Определить частоту колебаний, если минимальное расстояние между точками среды, фазы колебаний которых противоположны равно 0,75 м.
🎬 Видео
Уравнение равномерного движения. Решение задач по теме.Скачать

Решение графических задач на равномерное движениеСкачать

Уравнение равномерного прямолинейного движения | Физика 10 класс #3 | ИнфоурокСкачать

Физика - уравнения равноускоренного движенияСкачать

Движение точки тела. Способы описания движения | Физика 10 класс #2 | ИнфоурокСкачать

9 класс, 7 урок, Уравнение прямойСкачать

Уравнение прямой.Скачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Составляем уравнение прямой по точкамСкачать

Равномерное движение точки по окружности | Физика 10 класс #7 | ИнфоурокСкачать

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Вращательное движение. 10 класс.Скачать

11. Прямая в пространстве и ее уравненияСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Задача на движение материальной точки - bezbotvyСкачать

ЕГЭ по математике. Профильный уровень. Задание 7. Закон движения. ПроизводнаяСкачать

Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать