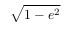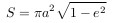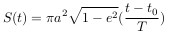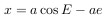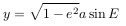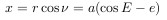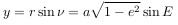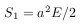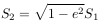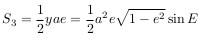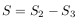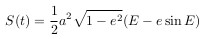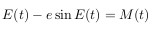Уравнение движения точки по эллипсу

Механическое состояние. Уравнение движения. Алгоритм численного решения. Системы взаимодействующих тел. Разные движения по эллипсам.

Механическое состояние. Уравнение движения.

При движении материальной точки изменяются со временем ее положение в пространстве, определяемое радиусом-вектором, ее скорость, ускорение. Говорят, что происходит изменение состояния материальной точки со временем. Что же понимают под механическим состоянием и какими параметрами оно определяется? Механическое состояние материальной точки в некоторый момент времени определено, если для этого момента времени заданы ее радиус-вектор и скорость.

Если известно механическое состояние материальной точки в какой-либо момент времени и действующие на нее силы, то с помощью второго закона Ньютона можно определить механическое состояние в последующие моменты времени, т. с. полностью предсказать движение. Именно по этой причине второй закон Ньютона часто называют уравнением движения, ибо он описывает эволюцию начального состояния механической системы во времени. Уравнение движения.

Остановимся подробнее на вопросе определения механического состояния в произвольный момент времени. Второй закон Ньютона, или уравнение движения, позволяет при известных силах найти ускорение материальной точки. Но знание ускорения дает возможность определить только изменение скорости за некоторый промежуток времени. Чтобы найти само значение скорости к концу этого промежутка, нужно знать не только изменение скорости, но и значение в начальный момент. Аналогично, знание скорости позволяет найти изменение положения материальной точки за некоторое время.

Чтобы найти сам радиус-вектор, нужно знать его значение в начальный момент. Например, в случае движения под действием постоянной силы, когда ускорение также постоянно, скорость и радиус-вектор материальной точки в момент времени определяются формулами скорость и радиус-вектор в начальный момент времени. Уравнение движения даст возможность найти только тогда, когда известно начальное состояние системы,величины.

Начальные условия.

Задание начальных условий для нахождения необходимо и в том случае, когда действующие силы таковы, что ускорение не остается постоянным. При этом в некоторых случаях уравнение движения удастся решить (проинтегрировать) аналитически, найти как функции времени, которые также будут содержать начальные значения.

В качестве примеров таких случаев можно указать движение материальной точки под действием силы, обратно пропорциональной квадрату расстояния от центра силового поля (движение планеты под действием притяжения к Солнцу, движение спутника Земли, движение альфа-частицы в поле атомного ядра), движение под действием силы, пропорциональной смещению от положения равновесия (тело на пружине).

По этой ссылке вы найдёте полный курс лекций по математике:

Алгоритм численного решения.

В случаях, когда уравнение движения не удается решить аналитически, его можно решать численно. Действующая на материальную точку сила может зависеть от времени явно, от положения точки и от ее скорости. Пусть нам заданы начальные значения. Уравнение движения дает возможность найти ускорение в тот же момент времени. Зная ускорение, можно приближенно найти изменение скорости за малый промежуток времени откуда скорость к концу этого промежутка равна Зная скорость в начальный момент, можно приближенно найти изменение радиуса-вектора за то же время.

Более точное значение можно получить, если взять вместо среднее значение скорости на этом промежутке, считая ускорение на нем постоянным: Отсюда значение радиуса-вектора к концу промежутка времени получится в виде в зависимости от того, какой из приведенных выше формул для отдать предпочтение. Выбор промежутка времени определяется той точностью, которую мы хотим получить при таком приближенном вычислении.

Чем меньше промежуток времени, тем ближе к истинным будут значения вычисляемые по формулам.

Найденные значения подставляем в выражение для силы и с помощью уравнения движения находим ускорение а, материальной точки в конце промежутка времени . Теперь повторяем описанную процедуру для следующего промежутка времени, причем роль начальных условий будут играть найденные по формулам и значения Затем все повторяется еще раз и т. д. Если требуется найти изменение механического состояния материальной точки за большой промежуток времени, придется разбить этот промежуток на большое число шагов. Чем меньше размер каждого шага, тем точнее будет результат.

Но необходимое число шагов при этом увеличивастся. За повышение точности результатов приходится платить увеличением объема вычислений. Практически такие работы удобно выполнять на ЭВМ. При проведении расчетов имеют дело не с векторами, а с числами. Поэтому каждое из приведенных выше векторных уравнений записывается в виде трех скалярных уравнений, соответствующих проекциям векторного уравнения на оси выбранной системы координат.

Возможно вам будут полезны данные страницы:

Системы взаимодействующих тел.

Часто приходится рассматривать механическую систему, состоящую из нескольких взаимодействующих тел. Если известны силы взаимодействия между телами и внешние силы, действующие на каждое из тел, то для нахождения движения всех этих тел приходится решать систему уравнений, состоящую из уравнений движения для каждого тела. Механическое состояние системы частиц определяется заданием положений и скоростей всех частиц в один и тот же момент времени. Уравнения движения позволяют найти изменение этого состояния со временем.

движении системы взаимодействующих тел обычно сопряжено с огромными математическими трудностями. Так, например, до сих пор не решена в общем виде задача о движении всего лишь трех взаимодействующих тел при произвольных начальных условиях. Однако численный расчет движения системы взаимодействующих частиц не содержит ничего принципиально нового по сравнению с расчетом движения одной материальной точки.

При приближенном вычислении скорость и радиус-вектор каждой из частиц находятся с помощью той же самой процедуры по формулам, только при определении ускорений частиц в каждый момент времени с помощью уравнений движения в этих уравнениях кроме внешних сил учитываются и силы взаимодействия между частицами.

• Какой смысл вкладывается в понятие механического состояния? Какими величинами определяется механическое состояние материальной точки? системы материальных точек?

• Почему ускорение частицы не входит в число величин, определяющих ее механическое состояние?

• Опишите алгоритм численного расчета механического движения материальной точки.

• Какую роль играют начальные условия при решении уравнений движения?

А Нахождение сил по движению. Уравнения движения можно использовать для нахождения действующих сил, если известно, как происходит движение тела, т. с. задан его радиус-вектор как функция времени. Примером такой задачи может служить нахождение силы притяжения планеты к Солнцу по известному из астрономических наблюдений закону обращения этой планеты по эллиптической орбите вокруг Солнца. Именно так был установлен закон обратных квадратов для силы тяготения.

Другой пример — движение точки по эллипсу, описываемое уравнениями В том, что траектория такого движения действительно представляет собой эллипс, можно убедиться, исключив время из этих уравнений. Разделив первое из этих уравнений, возводя их в квадрат и складывая, получим, учитывая тождество , следующую связь между: Это уравнение эллипса (рис. 102) с полуосями , которое в частном случае превращается в уравнение окружности.

Легко убедиться, что материальная точка движется по этому эллипсу в направлении против часовой стрелки, причем так, что ее радиус-вектор поворачивается с постоянной угловой скоростью. Для нахождения силы, вызывающей такое движение, нужно с помощью формул определить ускорение частицы. Дифференцируя уравнения по времени, находим проекции скорости на оси координат Дифференцируя по времени соотношения, получаем проекции ускорения.

Используя второй закон Ньютона и уравнения, получаем проекции силы, действующей на материальную точку массы. Сравнивая видим, что выражения для проекций силы можно записать в виде Эти соотношения дают искомую зависимость действующей на частицу силы от ее координат. В векторном виде их можно записать следующим образом Сила в каждой точке направлена к началу координат и пропорциональна расстоянию до находящегося там центра силового поля (см. рис. 102).

Такую зависимость силы от положения можно реализовать, например, с помощью двух пар одинаковых пружин (рис. 103). Чтобы движение тела происходило именно по уравнениям, начальные условия должны быть вполне определенными из следует, что при должно быть Рис. 103. При смещении шарика из положения равновесия действующая со стороны пружин сила направлена к этому положению равновесия и пропорциональна смещению из уравнений.

Такое начальное состояние можно осуществить, оттянув шарик в направлении оси на расстояние и толчком сообщив ему начальную скорость вдоль оси. При этом оси направлены вдоль недеформированных взаимно перпендикулярных пружин, а ось перпендикулярна плоскости, в которой они расположены. В действительности оказывается, однако, что взаимно перпендикулярные оси могут быть в плоскости пружин ориентированы произвольным образом.

Более того, если к этим двум парам пружин добавить еще такую же пару, расположенную перпендикулярно плоскости, в которой они лежат (рис. 104), то в такой системе выбор направления всех трех осей совершенно произволен. По своим механическим свойствам система оказывается изотропной. При любых начальных условиях траектория шарика будет плоской. Ориентация этой плоскости определяется векторами начального смещения и начальной скорости.

Разные движения по эллипсам.

Хотя движение тела под действием силы, пропорциональной смещению из положения равновесия, как и движение планет вокруг Солнца, происходит по эллиптической траектории, характер этих движений совершенно различен. Движение планеты происходит под действием силы, обратно пропорциональной квадрату расстояния до Солнца, расположенного в одном из фокусов эллипса (рис. 105), в то время как в рассмотренном выше примере шарика на пружинах силовой центр совпадает с центром эллипса. Различие в характере движений становится особенно отчетливым, если вспомнить, что вокруг Солнца скорость в афелии меньше, чем в перигелии.

Скорости планеты в афелии и перигелии, на концах большой полуоси эллипса, различны (рис. 105), в то время как у шарика на пружинах скорости в соответствующих точках орбиты одинаковы (см. рис. 102). Отметим, что в случае движения при наложенных связях механическое состояние определяется заданием значений обобщенных координат и значений скоростей их изменения (обобщенных скоростей) в один и тот же момент времени.

Таким образом, число параметров, определяющих механическое состояние системы, в два раза больше числа ее степеней свободы. Так, при движении точки по заданной окружности, сс механическое состояние определяется всего двумя величинами, например углом и угловой скоростью.

• Как показать, что радиус-вектор частицы, движение которой описывается уравнениями, поворачивается против часовой стрелки с постоянной угловой скоростью?

• Докажите, что формулы, связывающие проекции силы с координатами шарика, подвешенного на двух парах одинаковых пружин, справедливы при произвольной ориентации осей в плоскости пружин (т. с. оси не обязательно направлять вдоль пружин).

• Чем различаются движения по эллиптическим траекториям в случаях шарика, подвешенного на трех парах взаимно перпендикулярных одинаковых пружин, и орбитального движения планеты?

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Уравнение Кеплера

Статьи по небесной механике пользуются на Хабре некоторой популярностью, поэтому я решил рассказать
об одном фундаментальном уравнении движения, а именно, уравнении Кеплера.
Как известно, финитное движение небесных тел в Солнечной системе происходит по эллипсу. Однако, если необходимо
установить, в какой точке небесное тело находится в заданный момент времени, этой информации недостаточно и надо воспользоваться уравнением Кеплера.

Выведем это уравнение.
Напомню, что эллипс — это сплюснутая на величину

окружность. Здесь e — эксцентриситет.

Площадь эллипса равна

где a — большая полуось.
Согласно второму закону Кеплера, который гласит, что площадь, заметаемая радиус-вектором небесного тела пропорциональна времени, можно написать

где T — период обращения, t — текущее время, t0 — момент времени прохождения перигелия (ближайшей к Солнцу точки орбиты).

Найдем теперь зависимость этой площади от положения небесного тела на орбите, то есть от величины радиус-вектора r и истинной аномалии — угла между перигелием и небесным телом, если смотреть с Солнца.

Для этого введем дополнительную переменную — эксцентрическую аномалию E.
Направим ось x от Солнца (начала координат), которое находится в одном из фокусов эллипса, в сторону перигелия по линии апсид (прямой, соединяющей перицентр с апоцентром).
Создадим также вспомогательную окружность с радиусом, равным большой полуоси эллипса.

Абсцисса небесного тела в точке P будет равна

ордината будет, соответственно, равна

Таким образом, получаем

Для вычисления площади S рассмотрим вспомогательные фигуры:
сектор окружности P’-O-Per:

Сектор эллипса P-O-Per:

Отсюда, прощадь S равна:

Сравнивая это выражение с выведенным ранее из второго закона Кеплера,
получаем:

где M(t)=2*pi*(t — t0) / T

Это и есть уравнение Кеплера.

Заметим, что это трансцендентное уравнение относительно E и получить явное решение в общем случае не удается.

Для вычисления координат небесного тела необходимо найти эксцентрическую аномалию по известному M и e, a затем определить радиус-вектор и угол и, если необходимо x и y по приведенным выше формулам.

Интересным вопросом остается нахождение методов решения уравнения Кеплера.
Этим занимались лучшие умы человечества на протяжении последних четырехсот лет.
Результатом было обогащение математики множеством интересных идей, но описание этого требует отдельной статьи.

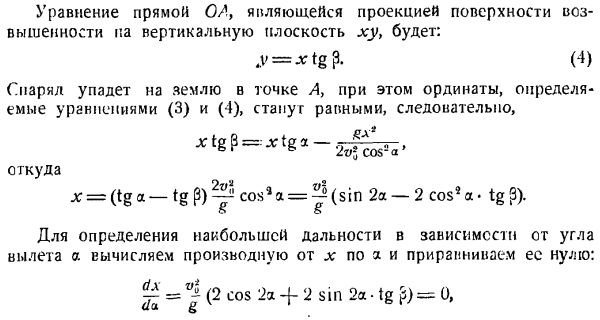
Видео:Равномерное движение точки по окружности | Физика 10 класс #7 | ИнфоурокСкачать

Траектория и уравнения движения точки

Видео:Траектория и уравнения движения точки. Задача 1Скачать

Траектория и уравнения движения точки

• Уравнение движения для локуса и точек 1°.Основные понятия. Траекторией точки называется линия, описываемая точкой движения в пространстве. Траектории могут быть плоскими или пространственными кривыми. Движение точки определяется установлением закона движения. Закон движения точек (уравнения) устанавливает зависимость расположения точек во временном пространстве.

Движение точки M в фиксированной системе координат xyz определяется установкой 3 функций (рис.3.1). * = / > ( ’). J’ = / *( Людмила Фирмаль

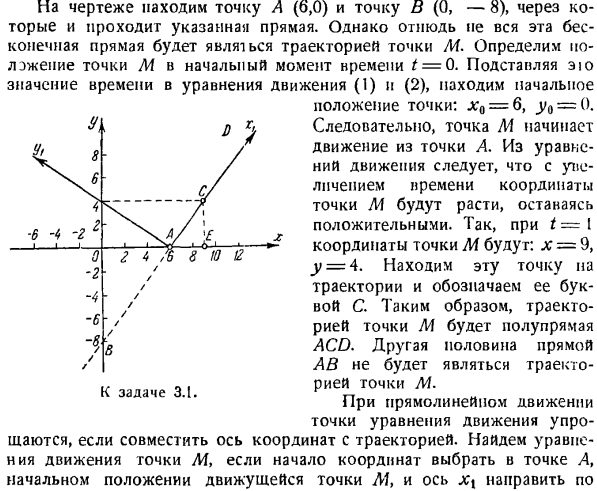
Создайте уравнение движения для точки N в декартовой системе координат. Найдите уравнение его орбиты. Определяет полный 1-кратный поворот точки N и точку, в которой координаты обеих точек равны. The solution. To составьте уравнение движения точки N, необходимо представить ее координаты в виде функции времени. Из рисунка найдите координату x в точке N. Х = О с COS Людмила Фирмаль

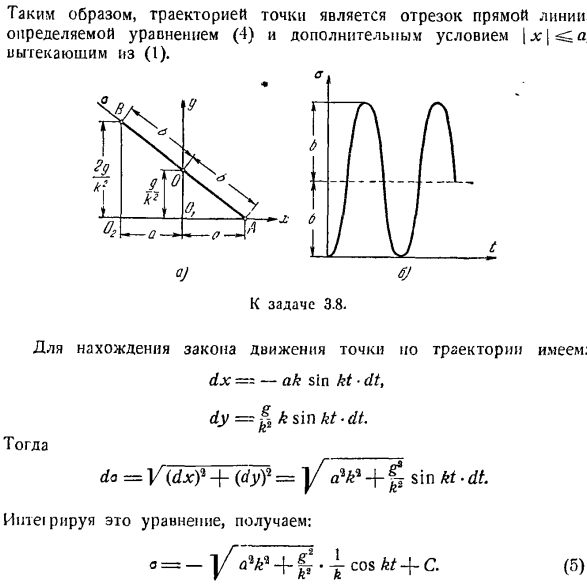
Затем по координатам определяется максимальное отклонение точки м от центра колебаний О. МПМ = а ХІ =-а. Величина a называется амплитудой колебаний, kt — (- (J называется фазой колебаний, ap-начальной фазой колебаний. Определите период колебаний, то есть время, в течение которого точки совершают 1 полное колебание, то есть возвращаются в исходное положение с той же скоростью и величиной. Обозначим период буквой Т и найдем его значение из условия, что приращение фазы колебаний за это время равно 2π. Иначе говоря

Задача 3.4.Точки перемещаются в соответствии с уравнением. x = A cos(kt-e), (1） г = Б, потому что КТ(2） Определите уравнение траектории движения точки. Как изменяется локус точек при увеличении разности фаз£от 0 до 2r? The solution. To найдя уравнение орбиты точки в явном виде, нужно исключить время из уравнения motion. To для этого сначала преобразуем уравнение движения. х = а соѕ(т-е)= а [потому что КТ потому что£-(- КТ грех грех ЭЖ.(3） решая уравнения (2) и (3) для cos kt и sin kt, получим: Х г — г соз£ а б. Преступление. потому что КТ =£о грех КТ = Добавьте эти уравнения, возведя их в квадрат. г, (т -£»»’) ’ 1 Б% ’ °1 (4） Sin2 е

Или в конце： — В + М — ^^ ко ^ грех ’、 уравнение (4) для любого значения e является уравнением эллипса. Из этого уравнения максимальные и минимальные значения являются Параметры±соответственно. a для x и zt b для y. таким образом, во всех случаях эллипс вписывается в прямоугольники со сторонами 2a и 2b. измените значение от 0 до 2ir. если e = 0, то выражение(4) принимает вид:

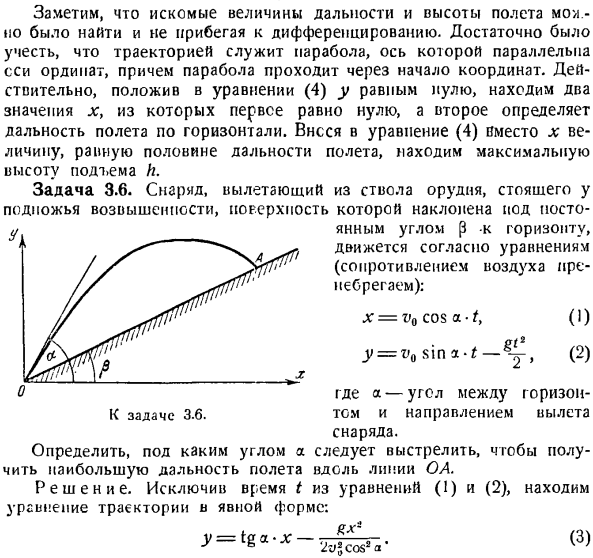
Так, если фазы обеих составляющих колебаний перпендикулярны друг другу, то эллипс вырождается в 2 совпадающие прямые, являющиеся диагоналями прямоугольника(рис. в коса -> -= учитывая it_y = 0, горизонтальная дальность полета I определяется из орбитального уравнения (4).

log A x cos2 a следовательно 2 значения x Т / л грех 2а х0 = 0, ХН = 1 = 8. Первое значение соответствует первому моменту (моменту отправления точки), А второе определяет горизонтальное расстояние. Сравнивая значения /и 5, можно сделать вывод, что/ = 2s, то есть точки достигают наивысшего положения в диапазоне горизонтальной половины. Итак, положение точки в пространстве в этой точке.

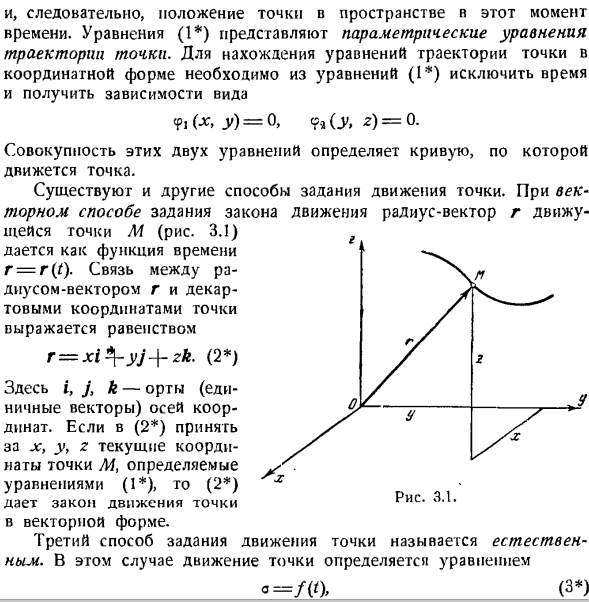
Уравнение (1) представляет собой параметрическое уравнение траектории a point. To найдя уравнение орбиты точки в координатной форме, нужно исключить время из уравнения(1) и получить форму зависимости. БФ,(Ци, г)= 0, 9а, КР, з)= 0. Комбинация этих 2 уравнений определяет кривую, по которой перемещаются точки. Есть и другие способы указать движение points. In векторным методом, определяющим законы движения, радиус-вектор r движущейся точки M (рис.3.1) задается как функция времени r = r (t).Связь между радиус-вектором r и Декартовыми координатами точки представлена уравнением Р = ХІ * — ый + ЗК. (2 ） Где i, j и k-единичные векторы (единичные векторы) осей. (2)

Если вы получаете x, y> z, текущие координаты точки A4, как определено y. уравнение(1), то (2) x Дайте закон движения точек в векторной форме. 3-й способ задания движения точек называется natural. In в этом случае движение точек определяется уравнением а = /( (). Сферические и цилиндрические координаты часто используются для изучения движения точки в пространстве. Сферическими координатами точки M (рис.3.4) являются расстояние r точки M от неподвижного центра O, угол φ (угол поворота плоскости zOM относительно неподвижной плоскости xOz) и угол ？ =?(’) * (5 *）

Уравнение движения для цилиндрических координат： р = п(о> т = м р = РЗ). (си *） м г Так… 1. Рисунок 3.4. Да. Чтобы перейти от сферических координат к декартовым, используйте следующую формулу:> х = р с с COS

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

🎥 Видео

Уравнение движенияСкачать

Физика 10 класс (Урок№4 - Равномерное движение точки по окружности.)Скачать

Физика - движение по окружностиСкачать

Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать

Движение материальной точки по окружности | Физика ЕГЭ, ЦТСкачать

Физика 10 Равномерное движение точки по окружностиСкачать

Сперматозоид-чемпион | наглядно показано оплодотворениеСкачать

Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать

Движение точки тела. Способы описания движения | Физика 10 класс #2 | ИнфоурокСкачать

Математика это не ИсламСкачать

К1 Определение скорости и ускорения точки по заданным уравнениям ее движенияСкачать

Криволинейное, равномерное движение материальной точки по окружности. Практическая часть. 9 класс.Скачать

Притворился новичком у репетитора по физике | ЕГЭ и ОГЭ по физике с Азатом АдеевымСкачать

Вращательное движение. 10 класс.Скачать

Кинематика точки Движение по окружностиСкачать

Ускорение при равномерном движении по окружностиСкачать