- теория по физике 🧲 кинематика
- Совместное движение двух тел
- Базовый уровень
- Уравнение движения тела дано в виде х = 4 — 3t. Определить начальную координату тела, скорость движения и перемещение тела за 2 секунды
- Ваш ответ
- решение вопроса
- Похожие вопросы
- Уравнение движения материальной точки
- Система отсчета. Системы координат
- Кинематическое уравнение движения материальной точки
- 📺 Видео
теория по физике 🧲 кинематика
Уравнение координаты — зависимость координаты тела от времени:
Уравнение координаты при равноускоренном прямолинейном движении:
x0 — координата тела в начальный момент времени, v0x —проекция начальной скорости на ось ОХ, ax —проекция ускорения на ось ОХ, x — координата тела в момент времени t
Зная уравнение координаты, можно определить координату тела в любой момент времени.
Пример №1. Движение автомобиля задано уравнением:
Определить начальное положение автомобиля относительно тела отсчета, его начальную скорость и ускорение. Также найти положение тела относительно тела отсчета в момент времени t = 10 c.
Уравнение координаты — это многочлен. В уравнении выше оно включает в себя только 2 многочлена. Первый — 15 — соответствует начальной координате тела. Поэтому x0 = 15. Коэффициент перед квадратом времени второго многочлена соответствует ускорению тела. Поэтому a = 5 м/с 2 . Второй многочлен отсутствует. Это значит, что коэффициент перед t равен 0. Поэтому начальная скорость тела равна нулю: v0 = 0 м/с.
В момент времени t = 10 c координата автомобиля равна:
Видео:Решение графических задач на равномерное движениеСкачать

Совместное движение двух тел
Иногда в одной системе отсчета рассматривается движение сразу двух тел. В этом случае движение каждого тела задается своим уравнением. Эти уравнения используются для нахождения различных параметров движения этих тел. Такой способ решения задач называется аналитическим.
Аналитический способ решения задачи на совместное движение тел
Чтобы найти место встречи двух тел, нужно:
- Построить уравнения зависимости x(t) обоих тел: x1(t) и x2(t).
- Построить уравнение вида x1 = x2.
- Найти время встречи двух тел tвстр.
- Подставить найденной время в любое из уравнений x1(t) или x2(t), чтобы вычислить координату xвстрч.
Пример №2. По одному направлению из одной точки начали двигаться два тела. Первое тело движется прямолинейно и равномерно со скоростью 3 м/с. Второе тело — равноускорено с ускорением 1 м/с 2 без начальной скорости. Определите, через какое время второе тело догонит первое. Вычислите, на каком расстоянии от тела отсчета это произойдет.
Составим уравнения для движения каждого из тел:
Приравняем правые части этих уравнений и найдем время t:
Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
Чтобы найти, какое расстояние они пройдут за это время, подставим известное время в любое из уравнений:
x = 3t = 3∙6 = 18 (м).
Графический способ решения задачи на совместное движение тел
Существует графический способ решения данной задачи. Для этого нужно:
- Построить графики x1(t) и x2(t).
- Найти точку пересечения графиков.
- Пустить перпендикуляр из этой точки к оси ОХ.
- Значение точки пересечения — координата места пересечения двух тел.
Таким способом можно определить, в какое время произойдет встреча двух тел. Нужно лишь провести перпендикуляр к оси времени после построения графиков перемещений.
Графический способ решения задач требует высокой точности построения графиков. Поэтому он применяется редко!
Если в одной системе описывается движение двух тел, и одно тело начинает движение с опозданием tзапазд, то его уравнение координаты принимает
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
Пример №3. Мальчики соревнуются в беге. По команде «Старт!» Миша побежал с ускорением 1 м/с 2 и через 4 секунды достиг максимальной скорости, с которой дальше продолжил движение. Саша отреагировал с опозданием и начал движение спустя 1 с после команды с ускорением 1,5 м/с 2 , достигнув максимальной скорости через 3 секунды. Найти время, через которое Саша догонит Мишу.
Если Саша догонит Мишу до того, как мальчики станут двигаться с равномерной скоростью, уравнение движения с равномерной скоростью можно игнорировать. Если это так, то корнем уравнения будет время, не превышающее 4 с (через столько времени оба мальчика начнут двигаться равномерно).
В таком случае составим уравнения только для тех участков пути, на которых мальчики двигались равноускорено:
Приравняем правые части уравнений и вычислим t:
В результате получаем два
Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
Материальная точка движется прямолинейно с постоянным ускорением. График зависимости её координаты от времени x=x(t) изображён на рисунке.
В момент времени t=0 проекции её скорости υx и ускорения ax на ось Ох удовлетворяют соотношениям:
а)
б)
в)
г)
Алгоритм решения
- Определить характер движения материальной точки.
- Записать уравнение координаты материальной точки.
- С помощью графика зависимости координаты от времени и уравнения координаты определить проекции искомых величин.
Решение Графиком зависимости координаты от времени является парабола. Такой график соответствует равноускоренному прямолинейному движению. Уравнение координаты при равноускоренном прямолинейном движении имеет
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алгоритм решения
- Записать исходные данные.
- Записать уравнение движения грузовика и преобразовать его с учетом условий задачи.
- Выразить скорость грузовика из уравнения его движения.
- Записать уравнение движения мотоциклиста.
- Найти время встречи мотоциклиста и грузовика из уравнения движения мотоциклиста.
- Подставить время в формулу скорости грузовика и вычислить ее.
Решение
- Координата встречи грузовика и мотоциклиста: x = 150 м.
- Время запаздывания мотоциклиста: tзапазд = 5 с.
- Ускорение, с которым мотоциклист начал движение: a = 3 м/с 2 .
Запишем уравнение движения грузовика:
Так как начальная координата равна нулю, это уравнение примет
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
Отсюда скорость движения грузовика равна:
Запишем уравнение движения мотоциклиста:
Так как начальная координата равна нулю, начальная скорость тоже нулевая, и мотоциклист начал движение позже грузовика, это уравнение примет вид:
Найдем время, через которое грузовик и мотоциклист встретились:
Подставим найденное время встречи в формулу для вычисления проекции скорости грузовика:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Видео:Траектория и уравнения движения точки. Задача 1Скачать

Базовый уровень
Велосипедист, двигаясь равномерно, проезжает 20м за 2с.
Определите, какой путь он проедет при движении с той же скоростью за 10с.
v=20:2=10м/c
s=10.10=100м
2. На рисунке 23 приведен график зависимости пути при движении
велосипедиста от времени. Определите по этому графику путь,
который проехал велосипедист в промежуток времени от 1 до 4с.

рис.23 рис.24 рис.25
3. По графику (см. рис.23) определите скорость движения велосипедиста
в момент времени t = 2c.
Ответ: v=3м/c
4. На рис.24 представлены графики движения трех тел.
Какое из этих тел движется с наибольшей по модулю скоростью
в момент времени t = 5c.
Ответ: v3=-4м/c
5. По графику (см. рис.24) определите скорость движения первого тела
в момент времени t = 5c.
Ответ: v=0
6. По графику (см. рис.25) определите время и место встречи первого и второго тел.
Ответ: t=5с x = 15м
7. Запишите уравнение движения x = x(t) второго тела (см. рис.25).
Ответ: x = 3 t.
8. Движение тела описывается уравнением x = 4 – t.
На каком из графиков (рис.26) представлена зависимость
координаты этого тела от времени?
Уравнение движения лыжника имеет вид х = –20+5t. Постройте график x(t).
Определите: а) координату лыжника через 10 с;
б) где был лыжник за 5 с до начала наблюдения;
в) когда он будет на расстоянии 80 м от начала координат.
а) t = 10c x = 30м
б) t = 5c x = -45м
в) х = 80м t = 20c
При движении вдоль оси ОХ координата точки изменилась за 8 с от значения x1=9 м до значения x2=17 м. Запишите формулу зависимости x(t). Скорость считать постоянной.
Вдоль оси ОХ движутся два тела, координаты которых изменяются согласно формулам: x1=10+2t и х2=4+5t. В какой момент времени тела встретятся?
Найдите координату точки встречи.
Вдоль оси ОХ движутся два тела, координаты которых изменяются согласно формулам: х1=20 — 4t и х2=10 + t. В какой момент времени тела встретятся?
Найдите координату точки встречи. Задачу решить графически.

зависимости vx(t).
Поезд длиной 240 м, двигаясь равномерно, прошел мост за 2 мин.
Какова скорость поезда, если длина моста 360 м?
 | ||||||
Последний вагон поезда проехал s=240+360=600м за t=120c, Автомобиль, двигаясь со скоростью 30 км/ч, проехал половину пути до места назначения за 2 ч. С какой скоростью он должен продолжить движение, чтобы достигнуть цели и вернуться обратно за то же время?
Движение материальной точки в плоскости ХОУ описывается уравнениями: х=6+3t, у=4t. На рисунке изображен график зависимости координаты материальной точки от времени. Построить график проекции скорости в зависимости от времени.
19. Наблюдая с платформы за равномерно движущимся поездом, мальчик определил,
Последний вагон поезда проехал мимо платформы длиной 120 м за 16 с, значит его скорость v=120/16=7,5м/с |

С какой скоростью он двигался, если увеличив скорость до 25 км/ч,
он за следующий час добрался до поселка Б и вернулся в поселок А?
v.1= 3s
v= 3s
Видео:Уравнение движения тела дано в виде x=2−3t. ВычислиСкачать

Уравнение движения тела дано в виде х = 4 — 3t. Определить начальную координату тела, скорость движения и перемещение тела за 2 секунды
Видео:Уравнение движенияСкачать

Ваш ответ
Видео:Физика - перемещение, скорость и ускорение. Графики движения.Скачать

решение вопроса
Видео:Урок 18 (осн). Координаты тела. График движения. График скоростиСкачать

Похожие вопросы
- Все категории
- экономические 43,429
- гуманитарные 33,634
- юридические 17,906
- школьный раздел 608,227
- разное 16,858
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:Физика - уравнения равноускоренного движенияСкачать

Уравнение движения материальной точки
Движение материальной точки в пространстве – это изменение ее положения относительно других тел с течением времени.
Имеет смысл говорить только о движении в некоторой системе отсчета.
Видео:Графическое представление равномерного движения.Скачать

Система отсчета. Системы координат
Точки, располагаемые в пустом пространстве, не различаются. Поэтому о точке рассуждают при условии нахождения в ней материальной точки. Определить ее положение можно при помощи измерений в системе координат, где и проводится нахождение пространственных координат. Если рассматривать в виде примера поверхность Земли, то следует учитывать широту и долготу располагаемой точки.
В теории используется декартова прямоугольная система координат, где определение точки возможно при наличии радиус-вектора r и трех проекций x , y , z – ее координат. Могут быть применены другие:
- сферическая система с положением точек и ее радиус-вектором, определенных координатами r , υ , φ ;
- цилиндрическая система с координатами p , z , α ;
- на полярной плоскости с параметрами r , φ .
В теории зачастую не принимают во внимание реальную систему отсчета, а сохраняют только ту, которая представляет собой ее математическую модель, применяемую во время практических измерений.
Видео:Движение точки тела. Способы описания движения | Физика 10 класс #2 | ИнфоурокСкачать

Кинематическое уравнение движения материальной точки
Любая система отсчета или координат предполагает определение координат материальной точки в любой момент времени.
При условии положения и определения материальной точки в данной системе отсчета считается, что ее движение задано или описано.
Это возможно при использовании кинематического уравнения движения:
Аналитически положение точки определяется совокупностью трех независимых между собой чисел. Иначе говоря, свободная точка имеет три степени свободы движения.
Ее перемещение по уравнению ( 1 ) определено, если имеется указанное положение в любой момент времени t . Для этого следует задавать декартовы координаты точки в качестве однозначных и непрерывных функций времени:
x ( t ) = x , y ( t ) = y , z ( t ) = z ( 2 ) .
Прямоугольные декартовы координаты x , y , z — это проекции радиус-вектора r ¯ , проведенного из начала координат. Очевидно, что длину и направление r ¯ можно найти из соотношений, где a , β , γ являются образованными радиус-вектором углами с координатными осями.
Равенства ( 2 ) считают кинематическими уравнениями движения материальной точки в декартовых координатах.
Они могут быть записаны в другой системе координат, которая связана с декартовой взаимно однозначным преобразованием. Если движение точки происходит в плоскости О х у , тогда применимы полярные координаты r , φ , относящиеся к декартовым преобразованиям. Данный случай подразумевает использование уравнения движения точки следующего вида:
r = r ( t ) , φ = φ ( t ) ( 3 ) .
Кинематическое уравнение движения точки в криволинейных координатах q 1 , q 2 , q 3 , связанных с декартовыми преобразованиями вида x = x ( q 1 , q 2 , q 3 ) , y = y ( q 1 , q 2 , q 3 ) , z = z ( q 1 , q 2 , q 3 ) ( 4 ) , записывается как
q 1 = q 1 ( t ) , q 2 = q 2 ( t ) , q 3 = q 3 ( t ) ( 5 ) .
Кривая радиус-вектора, описываемая концом вектора r при движении точки, совпадает с ее траекторией. Параметрическое уравнение траектории с t представлено кинематическими уравнениями ( 2 ) , ( 5 ) . Чтобы получить координатное уравнение траектории следует исключить время из кинематических уравнений.
Определение движения точки возможно с помощью задания траектории и мгновенного положения точки на ней. Ее положение на кривой определяется с помощью указания только одной величины: расстояния вдоль кривой от некоторой начальной точки с положительным направлением:
Это и есть уравнение движения точки по траектории. Способ его задания относят к естественному или траекторному.
Понятия координатного и естественного способа задания движения точки физически эквивалентны. С математической стороны это рассматривают как возможность применения разных методов, исходя из случая математической задачи.
Задание такого закона возможно аналитическим, графическим путем или с использованием таблицы, последние два из которых зачастую рассматривают в виде графиков и расписаний движений поездов.
Дано уравнение движения материальной точки x = 0 , 4 t 2 . Произвести запись формулы зависимости υ x ( t ) , построить график зависимости скорости от времени. На графике отметить площадь, численно равную пути, пройденному точкой за 4 секунды, произвести вычисление.
Дано: x = 0 , 4 t 2 , t = 4 c
Найти: υ x ( t ) , S — ?
Решение
При решении необходимо учитывать зависимость скорости от времени:
υ x = υ 0 x + a x t .
Зависимость координаты от времени и сравнение уравнения с заданным принимает вид:
x = x 0 + υ 0 x t + a x t 2 2 , x = 0 , 4 t 2 .
Очевидно, что x 0 = 0 , υ 0 x = 0 , a x = 0 , 8 м / с 2 .
После подстановки данных в уравнение:
Определим точки, изобразим график:
υ x = 0 , t = 0 , υ x = 4 , t = 5
Путь, по которому двигалось тело, равняется площади фигуры, ограниченной графиком, и находится с помощью формулы:
📺 Видео
Уравнение движения с постоянным ускорением | Физика 10 класс #6 | ИнфоурокСкачать

Уравнение равномерного прямолинейного движения | Физика 10 класс #3 | ИнфоурокСкачать

Урок 15. Решение задач на графики движенияСкачать

уравнение координаты материальной точки при равноускоренном движенииСкачать

Урок 12. Равномерное прямолинейное движениеСкачать

Графики зависимости пути и скорости от времениСкачать

Уравнение координат при равноускоренном движенииСкачать

Задача из ЕГЭ по физике │Анализ графика #1Скачать

Кинематика. Из координаты получаем скорость и ускорениеСкачать

Скорость прямолинейного равноускоренного движения. График скорости | Физика 9 класс #6 | ИнфоурокСкачать

Математика без Ху!ни. Нахождение асимптот, построение графика функции.Скачать
















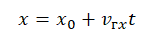
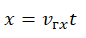

















 На рисунке изображен график зависимости координаты материальной точки от времени.
На рисунке изображен график зависимости координаты материальной точки от времени. 






