Уравнение движения тела закон сохранения импульса

Видео:Урок 104. Импульс. Закон сохранения импульсаСкачать

Закон cохранения импульса

О чем эта статья:

9 класс, 10 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Физика - импульс и закон сохранения импульсаСкачать

Импульс: что это такое

Как-то раз Рене Декарт (это который придумал ту самую декартову систему координат) решил, что каждый раз считать силу, чтобы описать процессы — как-то лень и сложно.

Для этого нужно ускорение, а оно не всегда очевидно. Тогда он придумал такую величину, как импульс. Импульс можно охарактеризовать, как количество движения — это произведение массы на скорость.

Импульс тела

p — импульс тела [кг · м/с]

m — масса тела [кг]

Видео:Импульс тела. Закон сохранения импульса | Физика 9 класс #20 | ИнфоурокСкачать

Закон сохранения импульса

В физике и правда ничего не исчезает и не появляется из ниоткуда. Импульс — не исключение. В замкнутой изолированной системе (это та, в которой тела взаимодействуют только друг с другом) закон сохранения импульса звучит так:

Закон сохранения импульса

Векторная сумма импульсов тел в замкнутой системе постоянна

А выглядит — вот так:

Закон сохранения импульса

p_n — импульс тела [кг · м/с]

Простая задачка

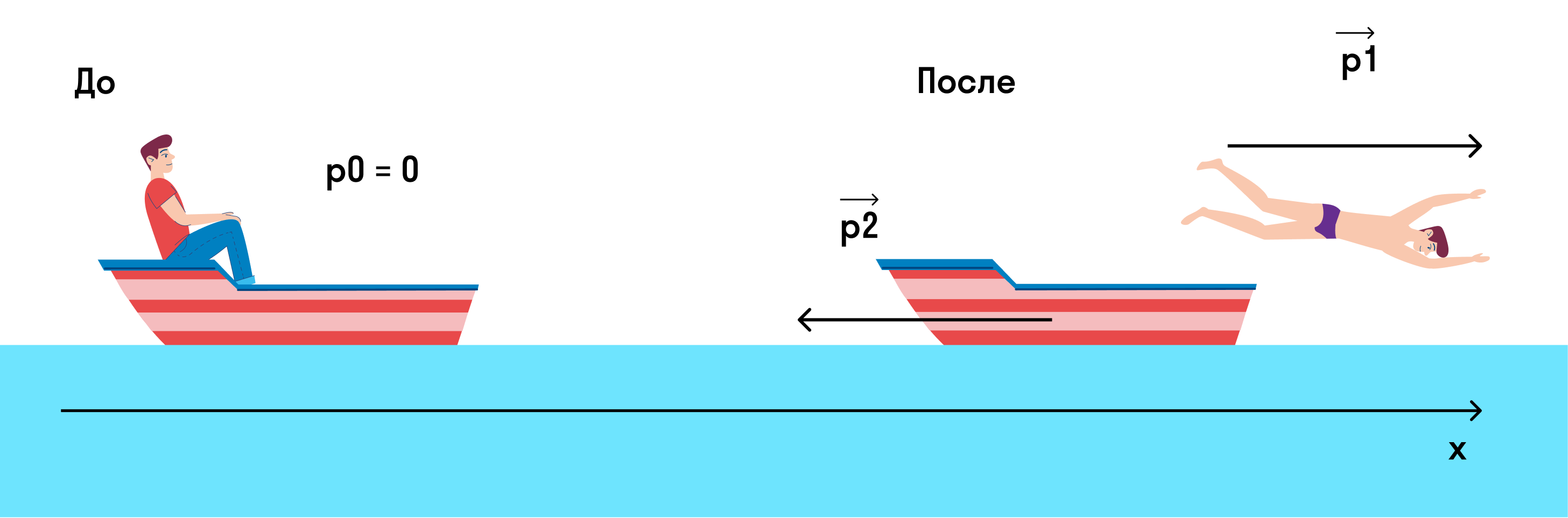
Мальчик массой m = 45 кг плыл на лодке массой M = 270 кг в озере и решил искупаться. Остановил лодку (совсем остановил, чтобы она не двигалась) и спрыгнул с нее с горизонтально направленной скоростью 3 м/с. С какой скоростью станет двигаться лодка?

Решение:

Запишем закон сохранения импульса для данного процесса.

— это импульс системы мальчик + лодка до того, как мальчик спрыгнул,

— это импульс мальчика после прыжка,

— это импульс лодки после прыжка.

Изобразим на рисунке, что происходило до и после прыжка.

Если мы спроецируем импульсы на ось х, то закон сохранения импульса примет вид

Подставим формулу импульса.
, где:
— масса мальчика [кг]
— скорость мальчика после прыжка [м/с]
— масса лодки [кг]
— скорость лодки после прыжка [м/с]

Выразим скорость лодки :

Подставим значения:
м/с

Ответ: скорость лодки после прыжка равна 0,5 м/с

Задачка посложнее

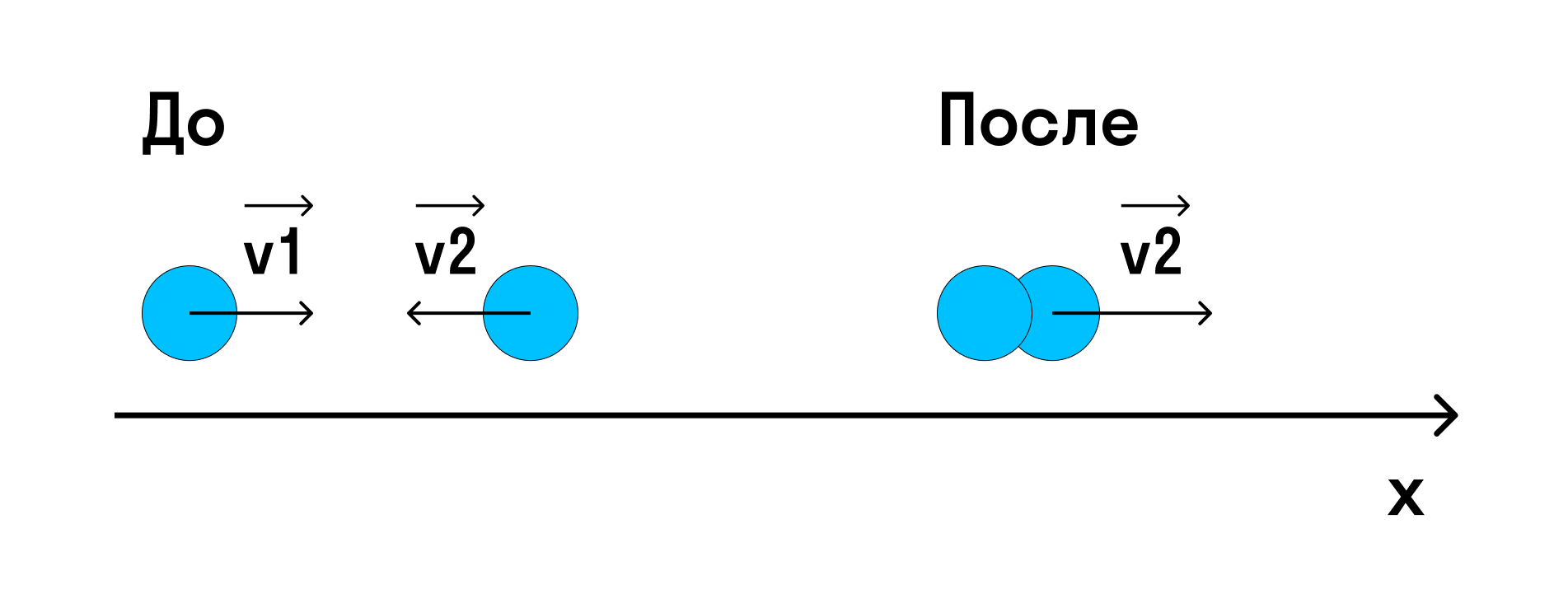
Тело массы m₁ = 800 г движется со скоростью v₁ = 3 м/с по гладкой горизонтальной поверхности. Навстречу ему движется тело массы m₂ = 200 г со скоростью v₂ = 13 м/с. Происходит абсолютно неупругий удар (тела слипаются). Найти скорость тел после удара.

Решение: Для данной системы выполняется закон сохранения импульса:

Импульс системы до удара — это сумма импульсов тел, а после удара — импульс «получившегося» в результате удара тела.

Спроецируем импульсы на ось х:

После неупругого удара получилось одно тело массы , которое движется с искомой скоростью:

Отсюда находим скорость тела, образовавшегося после удара:

Переводим массу в килограммы и подставляем значения:

В результате мы получили отрицательное значение скорости. Это значит, что в самом начале на рисунке мы направили скорость после удара неправильно.

Знак минус указывает на то, что слипшиеся тела двигаются в сторону, противоположную оси X. Это никак не влияет на получившееся значение.

Ответ: скорость системы тел после соударения равна v = 0,2 м/с.

Видео:Физика 10 класс (Урок№11 - Импульс. Закон сохранения импульса.)Скачать

Второй закон Ньютона в импульсной форме

Второй закон Ньютона в импульсной форме можно получить следующим образом. Пусть для определенности векторы скоростей тела и вектор силы направлены вдоль одной прямой линии, т. е. движение прямолинейное.

Запишем второй закон Ньютона, спроецированный на ось х, сонаправленную с направлением движения и ускорением:

Применим выражение для ускорения

В этих уравнениях слева находится величина a. Так как левые части уравнений равны, можно приравнять правые их части

Полученное выражение является пропорцией. Применив основное свойство пропорции, получим такое выражение:

В правой части находится — это разница между конечной и начальной скоростью.

Преобразуем правую часть

Раскрыв скобки, получим

Заменим произведение массы и скорости на импульс:

То есть, вектор – это вектор изменения импульса .

Тогда второй закон Ньютона в импульсной форме запишем так

Вернемся к векторной форме, чтобы данное выражение было справедливо для любого направления вектора ускорения.

Задачка про белку отлично описывает смысл второго закона Ньютона в импульсной форме

Белка с полными лапками орехов сидит на гладком горизонтальном столе. И вот кто-то бесцеремонно толкает ее к краю стола. Белка понимает законы Ньютона и предотвращает падение. Но как?

Решение:

Чтобы к белке приложить силу, которая будет толкать белку в обратном направлении от края стола, нужно создать соответствующий импульс (вот и второй закон Ньютона в импульсной форме подъехал).

Ну, а чтобы создать импульс, белка может выкинуть орехи в сторону направления движения — тогда по закону сохранения импульса ее собственный импульс будет направлен против направления скорости орехов.

Видео:ФИЗИКА 9 класс. Импульс тела. Закон сохранения импульса | ВидеоурокСкачать

Реактивное движение

В основе движения ракет, салютов и некоторых живых существ: кальмаров, осьминогов, каракатиц и медуз — лежит закон сохранения импульса. В этих случаях движение тела возникает из-за отделения какой-либо его части. Такое движение называется реактивным.

Яркий пример реактивного движения в технике — движение ракеты, когда из нее истекает струя горючего газа, которая образуется при сгорании топлива.

Сила, с которой ракета действует на газы, равна по модулю и противоположна по направлению силе, с которой газы отталкивают от себя ракету:

Сила называется реактивной. Это та сила, которая возникает в процессе отделения части тела. Особенностью реактивной силы является то, что она возникает без взаимодействия с внешними телами.

Закон сохранения импульса позволяет оценить скорость ракеты.

v_г — скорость горючего,

v_р — скорость ракеты.

Отсюда можно выразить скорость ракеты:

Скорость ракеты при реактивном движении

v_г — скорость горючего [м/с]

m_р — масса ракеты [кг]

v_р — скорость ракеты [м/с]

Эта формула справедлива для случая мгновенного сгорания топлива. Мгновенное сгорание — это теоретическая модель. В реальной жизни топливо сгорает постепенно, так как мгновенное сгорание приводит к взрыву.

Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!

Видео:Импульс тела и импульс силы. Закон сохранения импульса. 10 класс.Скачать

Закон сохранения импульса. Реактивное движение

Видео:Закон сохранения импульсаСкачать

Закон сохранения импульса

Закон сохранения импульса можно наблюдать повсюду. Он достаточно точно выполняется в реальных условиях, если пренебречь сопротивлением воздуха, силами трения и т.д. Примеры проявления этого закона:

• стрелок ощущает отдачу при выстреле из ружья;
• рыбак переходит с кормы на нос лодки, а лодка при этом движется в противоположную сторону;
• шары сталкиваются на бильярдном столе.

Однако, прежде чем говорить о законе сохранении импульса, рассмотрим понятие замкнутой системы.

Замкнутая система — система тел, на которую со стороны других тел не действуют внешние силы.

Формулировка закона сохранения импульса (ЗСИ)

Векторная сумма импульсов всех тел, входящих в замкнутую систему, остается постоянной при любых взаимодействиях этих тел между собой внутри системы.

Данный закон является следствием из второго и третьего законов Ньютона. Покажем это.

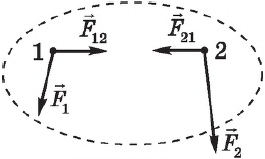
Возьмем замкнутую систему из двух взаимодействующих тел. Силы F 1 → и F 2 → — это силы взаимодействия между телами. Третий закон Ньютона гласит, что F 2 → = — F 1 → . Пусть тела взаимодействуют во течение времени t . Тогда импульсы сил одинаковы по модулю и противоположны по направлению, как и сами силы.

F 2 t → = — F 1 → t .

По второму закону Ньютона:

F 1 → t = m 1 v 1 ‘ → — m 1 v 1 → ; F 2 → t = m 1 v 2 ‘ → — m 1 v 2 →

Здесь v 1 ‘ → и v 2 ‘ → — скорости тел в конце взаимодействия. Соответственно, скорости без штрихов обозначают эти величины в начальный момент взаимодействия.

Из записанного выше следует соотношение:

m 1 v 1 → + m 2 v 2 → = m 1 v 1 ‘ → + m 2 v 2 ‘ →

Это равенство — математическая форма записи закона сохранения импульса. Оно означает, что суммарный импульс системы в результате какого-то взаимодействия не изменился.

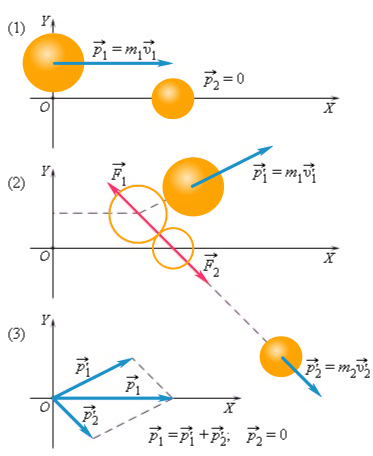
Проиллюстрируем закон сохранения импульса на примере соударения шаров разных масс. Один из шаров до удара покоился.

Как видим, после удара векторная сумма импульсов двух шаров равна первоначальному импульсу движущегося шара.

Важно! Закон сохранения выполняется и для проекций векторов на координатные оси.

Закон сохранения импульса позволяет решать задачи и находить скорости тел не зная значений действующих сил.

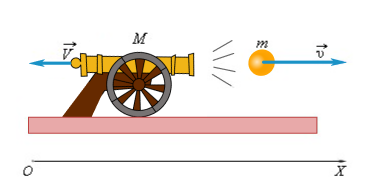
Рассмотрим снаряд, вылетающий из пушки.

В данном случае взаимодействующие тела — это снаряд и пушка. Сначала тела не движутся. При выстреле снаряд приобретает скорость v → и летит вперед, а пушка откатывается назад со скоростью V → . Откатывание пушки называется отдачей от выстрела.

По закону сохранения импульса в проекции на ось OX можно записать:

Видео:Закон сохранения импульса. Реактивное движение | Физика 10 класс #17 | ИнфоурокСкачать

Реактивное движение

Реактивное движение также основано на принципе отдачи. Нагретые газы выбрасываются из сопла реактивного двигателя со скоростью u → . Пусть масса газов равна m , а масса ракеты после истечения газов — M . Рассматривая замкнутую систему «ракета-газы» и применяя к ней закон сохранения импульса, можно вычислить скорость ракеты V после истечения газов.

Формула для пушки и снаряда не применима к ракете, так как дает лишь приблизительное представление о движении ракеты, На самом деле вся масса газов выходит из сопла не сразу, а постепенно.

Рассмотрим этот процесс подробнее. Пусть масса ракеты в момент времени t равна M , а сама ракета движется со скоростью v → . В течение малого промежутка времени ∆ t из сопла ракеты выбрасывается порция газа с относительной скоростью u → . По истечении времени ∆ t ракета будет двигаться со скоростью v + ∆ v , а масса ракеты станет равной M — ∆ M .

В момент t + ∆ t импульс ракеты равен:

Импульс реактивных газов:

По закону сохранения импульса:

M v → = M — ∆ M · v → + ∆ v → + ∆ M · v → + u → .

M ∆ v → = ∆ M · u → — ∆ M · ∆ v → .

​​​​​​​

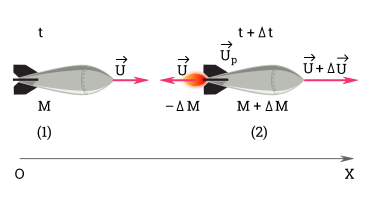
Величиной ∆ M · ∆ v → можно пренебречь, так как ∆ M намного меньше M .

Разделим последнее равенство на ∆ t и перейдем к пределу ∆ t → 0 .

M ∆ v → ∆ t = ∆ M · u → ∆ t ( ∆ t → 0 )

Здесь μ — расход топлива в единицу времени, а — μ u → — реактивная сила тяги. Направление этой силы совпадает с направлением движения ракеты.

Формула M a → = — μ u → выражает второй закон Ньютона для тела переменной массы. В скалярном виде ее можно переписать так:

Конечная скорость ракеты определяется по формуле:

Это так называемая формула Циолковского, согласно которой конечная скорость ракеты может превышать скорость истечения газов из сопла двигателя. Правда, достижение такой скорости связано с определенными сложностями. Во-первых, такими, как значительный расход топлива.

Для того, чтобы развить первую космическую скорость v = v 1 = 7 , 9 · 10 3 м с при скорости истечения газов u = 3 · 10 3 м с стартовая масса ракеты должна быть примерно в 14 раз больше конечной массы.

Современное ракетостроение развивается в направлении экономичных многоступенчатых ракет. Сброс отсеков с отработанным топливом позволяет значительно сократить массу ракеты и оптимизировать дальнейший расход топлива для ее разгона.

Видео:Физика. Задача на импульс тела. Закон сохранения импульса.Скачать

Закон сохранения импульса, кинетическая и потенциальные энергии, мощность силы

Видео:ИМПУЛЬС ТЕЛА закон сохранение импульса 9 классСкачать

Теория к заданию 3 из ЕГЭ по физике

Импульс тела

Импульсом тела называется величина, равная произведению массы тела на его скорость.

Следует помнить, что речь идет о теле, которое можно представить как материальную точку. Импульс тела ($р$) называют также количеством движения. Понятие количества движения было введено в физику Рене Декартом (1596—1650). Термин «импульс» появился позже (impulsus в переводе с латинского означает «толчок»). Импульс является векторной величиной (как и скорость) и выражается формулой:

Направление вектора импульса всегда совпадает с направлением скорости.

За единицу импульса в СИ принимают импульс тела массой $1$ кг, движущегося со скоростью $1$ м/с, следовательно, единицей импульса является $1$ кг $·$ м/с.

Если на тело (материальную точку) действует постоянная сила в течение промежутка времени $∆t$, то постоянным будет и ускорение:

где, $↖$ и $↖$ — начальная и конечная скорости тела. Подставив это значение в выражение второго закона Ньютона, получим:

Раскрыв скобки и воспользовавшись выражением для импульса тела, имеем:

Здесь $

↖-

↖=∆p↖$ — изменение импульса за время $∆t$. Тогда предыдущее уравнение примет вид:

Выражение $∆p↖=F↖∆t$ представляет собой математическую запись второго закона Ньютона.

Произведение силы на время ее действия называют импульсом силы. Поэтому изменение импульса точки равно изменению импульса силы, действующей на нее.

Выражение $∆p↖=F↖∆t$ называется уравнением движения тела. Следует заметить, что одно и то же действие — изменение импульса точки — может быть получено малой силой за большой промежуток времени и большой силой за малый промежуток времени.

Импульс системы тел. Закон изменения импульса

Импульсом (количеством движения) механической системы называется вектор, равный сумме импульсов всех материальных точек этой системы:

Законы изменения и сохранения импульса являются следствием второго и третьего законов Ньютона.

Рассмотрим систему, состоящую из двух тел. Силы ($F_$ и $F_$ на рисунке, с которыми тела системы взаимодействуют между собой, называются внутренними.

Пусть кроме внутренних сил на систему действуют внешние силы $↖$ и $↖$. Для каждого тела можно записать уравнение $∆p↖=F↖∆t$. Сложив левые и правые части этих уравнений, получим:

В левой части стоит геометрическая сумма изменений импульсов всех тел системы, равная изменению импульса самой системы — $<∆p_>↖$.С учетом этого равенство $↖+↖=(↖+↖)∆t$ можно записать:

где $F↖$ — сумма всех внешних сил, действующих на тело. Полученный результат означает, что импульс системы могут изменить только внешние силы, причем изменение импульса системы направлено так же, как суммарная внешняя сила. В этом суть закона изменения импульса механической системы.

Внутренние силы изменить суммарный импульс системы не могут. Они лишь меняют импульсы отдельных тел системы.

Закон сохранения импульса

Из уравнения $<∆p_>↖=F↖∆t$ вытекает закон сохранения импульса. Если на систему не действуют никакие внешние силы, то правая часть уравнения $<∆p_>↖=F↖∆t$ обращается в ноль, что означает неизменность суммарного импульса системы:

Система, на которую не действуют никакие внешние силы или равнодействующая внешних сил равна нулю, называется замкнутой.

Закон сохранения импульса гласит:

Суммарный импульс замкнутой системы тел остается постоянным при любых взаимодействиях тел системы между собой.

Полученный результат справедлив для системы, содержащей произвольное число тел. Если сумма внешних сил не равна нулю, но сумма их проекций на какое-то направление равна нулю, то проекция импульса системы на это направление не меняется. Так, например, система тел на поверхности Земли не может считаться замкнутой из-за силы тяжести, действующей на все тела, однако сумма проекций импульсов на горизонтальное направление может оставаться неизменной (при отсутствии трения), т. к. в этом направлении сила тяжести не действует.

Реактивное движение

Рассмотрим примеры, подтверждающие справедливость закона сохранения импульса.

Возьмем детский резиновый шарик, надуем его и отпустим. Мы увидим, что когда воздух начнет выходить из него в одну сторону, сам шарик полетит в другую. Движение шарика является примером реактивного движения. Объясняется оно законом сохранения импульса: суммарный импульс системы «шарик плюс воздух в нем» до истечения воздуха равен нулю; он должен остаться равным нулю и во время движения; поэтому шарик движется в сторону, противоположную направлению истечения струи, и с такой скоростью, что его импульс по модулю равен импульсу воздушной струи.

Реактивным движением называют движение тела, возникающее при отделении от него с какой- либо скоростью некоторой его части. Вследствие закона сохранения импульса направление движения тела при этом противоположно направлению движения отделившейся части.

На принципе реактивного движения основаны полеты ракет. Современная космическая ракета представляет собой очень сложный летательный аппарат. Масса ракеты складывается из массы рабочего тела (т. е. раскаленных газов, образующихся в результате сгорания топлива и выбрасываемых в виде реактивной струи) и конечной, или, как говорят, «сухой» массы ракеты, остающейся после выброса из ракеты рабочего тела.

Когда реактивная газовая струя с большой скоростью выбрасывается из ракеты, сама ракета устремляется в противоположную сторону. Согласно закону сохранения импульса, импульс $m_

υ_p$, приобретаемый ракетой, должен быть равен импульсу $m_·υ_$ выброшенных газов:

Отсюда следует, что скорость ракеты

Из этой формулы видно, что скорость ракеты тем больше, чем больше скорость выбрасываемых газов и отношение массы рабочего тела (т. е. массы топлива) к конечной («сухой») массе ракеты.

Формула $υ_p=(<m_>/)·υ_$ является приближенной. В ней не учитывается, что по мере сгорания топлива масса летящей ракеты становится все меньше и меньше. Точная формула для скорости ракеты была получена в 1897 г. К. Э. Циолковским и носит его имя.

Формула Циолковского позволяет рассчитать запасы топлива, необходимые для сообщения ракете заданной скорости.

Работа силы

Термин «работа» был введен в физику в 1826 г. французским ученым Ж. Понселе. Если в обыденной жизни работой называют лишь труд человека, то в физике и, в частности, в механике принято считать, что работу совершает сила. Физическую величину работы обычно обозначают буквой $А$.

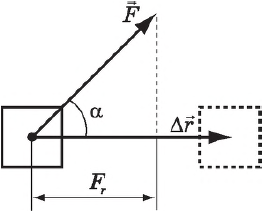
Работа силы — это мера действия силы, зависящая от ее модуля и направления, а также от перемещения точки приложения силы. Для постоянной силы и прямолинейного перемещения работа определяется равенством:

где $F$ — сила, действующая на тело, $∆r↖$ — перемещение, $α$ — угол между силой и перемещением.

Работа силы равна произведению модулей силы и перемещения и косинуса угла между ними, т. е. скалярному произведению векторов $F↖$ и $∆r↖$.

Работа — величина скалярная. Если $α 0$, а если $90° А_п$, КПД всегда меньше $1$ (или $

🎬 Видео

Физика | Закон сохранения импульсаСкачать

Урок 107. Задачи на закон сохранения импульса (ч.1)Скачать

Физика 9 класс. §20 Закон сохранения импульсаСкачать

Закон сохранения импульса. Решение задач. 9 классСкачать

Закон сохранения импульса. Практическая часть - решение задачи. 9 класс.Скачать

Импульс тела. Закон сохранения импульса (учебный фильм)Скачать

Что такое импульс? Закон сохранения импульса #Shorts #ОГЭ #ФизикаСкачать

Закон Сохранения Импульса за 1 минуту #global_ee #егэфизика #огэфизикаСкачать

Физика 9 класс Закон сохранения импульсаСкачать

Физика 10 класс. Закон сохранения импульса Решение задачСкачать