Основная задача расчета орбитального движения спутника состоит в том, чтобы по его координатам и скорости, известным в начальный момент времени в заданной системе отсчета, определить координаты и скорость в любой последующий момент времени в произвольной системе отсчета.
Предполагается, что векторы (vec) и (vec) , определяющие положение и скорость спутника, задаются в инерциальной системе координат. Уравнения движения спутника имеют вид
где (vec) — ускорение спутника, равное
(vec_E) — ускорение, обусловленное действием поля тяготения Земли;
(vec_S) — ускорение, вызванное притяжением Солнца;
(vec_M) — ускорение, вызванное притяжением Луны;
(vec_a) — ускорение, обусловленное сопротивлением движению в атмосфере;
(vec_p) — ускорение, вызванное давлением солнечного излучения.
Численное интегрирование уравнений (ref) является основой расчета орбитального движения спутника. Для этого необходимо знать выражения сил, действующих на спутник в околоземном пространстве.
- Модели сил гравитационного притяжения
- Поле тяготения Земли
- Приливные деформации Земли
- Притяжение Солнца и Луны
- Более точное определение положений Солнца и Луны
- Эффекты общей теории относительности
- Модели гравитационного поля Земли
- Модели сил негравитационной природы
- Сопротивление атмосферы
- Экспоненциальная атмосфера
- Модель Харриса-Прейстера (Harris-Priester)
- Современные модели атмосферы
- Солнечное давление
- Давление излучения Земли
- Программное обеспечение расчета орбитального движения спутника
- 3. ОРБИТЫ ИСКУССТВЕННЫХ СПУТНИКОВ ЗЕМЛИ.
- Наблюдение искусственных спутников Земли
- Глава 1: Как движутся ИСЗ?
- § 1. Законы Кеплера и типы орбит
- § 2. Орбитальные элементы
- § 3. Круговая орбита
- § 4. Эллиптическая орбита
- § 5. Эволюция орбиты ИСЗ
- Прецессия орбиты
- Вращение эллиптической орбиты
- Атмосферное торможение
- Давление света
- 🎦 Видео
Видео:Урок 64. Искусственные спутники Земли. Первая космическая скорость. Геостационарная орбитаСкачать

Модели сил гравитационного притяжения
Поле тяготения Земли
Потенциал поля тяготения Земли удобно определять в геоцентрической экваториальной системе координат, вращающейся вместе с Землей. Связь между декартовыми ((x, y, z)) и полярными координатами ((r, varphi, lambda)) задается формулами (рис.)
где (varphi) — широта;
(r) — расстояние от начала координат до точки наблюдения.
Согласно [1], потенциал поля тяготения Земли записывается в виде разложения в ряд по сферическим функциям
где (mu = 398600,4415) км (^3) /c (^2) — гравитационная постоянная Земли;
(R = 6378,137) км — радиус Земли;
(P_) — присоединенная функция Лежандра степени (n) и порядка (m) ;
(C_) и (S_) — коэффициенты, зависящие от распределения масс внутри Земли и задаваемые таблично.
Для удобства вычислений введем следующие обозначения
Тогда выражение для потенциала поля тяготения Земли (ref) приобретет вид
Для вычисления присоединенных функций Лежандра степени (n) и порядка (m) используются рекуррентные соотношения. Так, все функции вида (P_) , начиная с (P_=1) , вычисляются при помощи формулы
где (u = sinvarphi) , ((1-u^2)^ = cosvarphi) .
Оставшиеся функции вычисляются из соотношений
Пользуясь известными выражениями для сумм тригонометрических функций
и соотношениями (ref)—(ref), запишем рекуррентные формулы для вычисления (V_) и (W_)
Отметим, что для вычисления (V_) и (W_) удобно использовать частный случай формулы (ref)
Вычисления (V_) и (W_) производятся в следующем порядке.
Значения (V_) и (W_) известны и равны
Пользуясь ими, вычислим:
Затем цикл вычислений повторяется:
Таким образом, вычисления (рис.) выполняются слева направо и сверху вниз. Стрелка (downarrow) означает расчет по формулам (ref) (или (ref), как частному случаю (ref)), а (searrow) — по формулам (ref).
Ускорение (ddot<vec>) , равное градиенту потенциала (U) , в декартовых координатах запишется как
где (ddot x_) , (ddot y_) и (ddot z_) определяются по формулам
Приливные деформации Земли
Согласно [2], возмущения от приливных деформаций центрального тела вносят заметный вклад в возмущения искусственных спутников Земли.
Гравитационное воздействие сторонних тел, таких как Луна и Солнце, приводит к деформации Земли, вследствие чего изменяется её гравитационное поля. Простейшей моделью представления потенциала действующих на спутник сил, обусловленных приливными деформациями Земли, является модель Лява (Love) или модель твердых приливов [2].
В этой модели приливный потенциал приводит к упругой деформации Земли, изменяющей потенциал её гравитационного поля, причем изменение потенциала линейным образом связано с приливным потенциалом через так называемое число Лява.
Более точные модели учитывают влияние приливных деформаций, возникающих в океане и в атмосфере Земли. В этом случае влияние приливов может быть выражено в виде поправок к коэффициентам геопотенциала (C_) , (S_) , учитывающих неупругие деформации и периодические вариации чисел Лява (модель Вара (Wahr) [2]).
Притяжение Солнца и Луны
В инерциальной системе координат ускорение спутника, вызываемое притяжением точечной массы (M) (материальной точки), равно
где (vec) и (vec) — геоцентрические координаты спутника и (M) соответственно.
Следует учесть, что под действием притяжения (M) центр масс Земли, в свою очередь, приобретает ускорение
В результате, ускорение спутника в относительной системе координат связанной с центром масс Земли равно разности ускорений (ref) и (ref)
Возмущающие влияния Солнца и Луны принято считать независимыми друг от друга, поэтому формулой (ref) можно пользоваться в обоих случаях.
Для вычисления силы притяжения по формуле (ref) необходимо знать координаты возмущающего тела. Во многих случаях для этого достаточно использовать простые уравнения, которые следуют из аналитических теорий движения Солнца (Ньюкома) и Луны (Брауна) и обеспечивают отклонение, не превышающее (1%) от наиболее совершенных современных теорий [1].
Геоцентрические координаты Солнца можно получить, предполагая что Земля совершает невозмущенное движение вокруг Солнца по эллиптической орбите с параметрами
где (T = (JD — 2451545,0)/36525,0) — число юлианских столетий, прошедших с эпохи J2000.
В астрономии эпоха — это момент времени, указанный в какой-либо шкале времени. Эпоха J2000 — полдень ( (12^h) ) 1 января 2000 г. по земному времени TT (Terrestrial Time) — стандартная эпоха современных астрономических расчетов.
С учетом малости эксцентриситета и наклонения, координаты Солнца представляются в форме рядов [1]
где (lambda_odot) и (r_odot) — геоцентрические эклиптические долгота и расстояние до Солнца соответственно. Отметим, что геоцентрическая эклиптическая широта Солнца (beta_odot) равна нулю с точностью не хуже (1^prime) [1].
Переход к прямоугольным экваториальным координатам осуществляется по формулам
где (epsilon = 23^circ,43929111) — наклон эклиптики относительно земного экватора;
С учетом равенства (beta_odot = 0) , получим из (ref)
Координаты (lambda_odot) , (beta_odot) и (r_odot) в (ref) относятся к среднему равноденствию и эклиптике в эпоху J2000.
Прецессия, являющаяся результатом действия возмущающих сил Солнца, Луны и планет, приводит к медленному движению как эклиптики так и равноденствия. Плоскость эклиптики меняет свою ориентацию сравнительно медленно — менее чем на (1^prime) в столетие. Движение равноденствия более выраженно и составляет (5030^pprime) в столетие. Поэтому, для того, чтобы найти координаты равноденствия в некоторую эпоху (T_text) (измеряется в столетиях с начала эпохи J2000), нужно добавить к (lambda_odot) следующую поправку
Эклиптическая широта (beta_odot) в поправках не нуждается, так как изменяется не более чем на (1^prime) за столетие.
Таким образом, формулы (ref) и (ref) с учетом (ref) позволяют вычислить прямоугольные координаты Солнца в геоцентрической экваториальной системе координат.
Разложения в ряды, аналогичные (ref), существуют и для координат Луны. Однако, в связи с тем, что Луна испытывает сильные возмущения со стороны Солнца и Земли, для описания ее движения необходимо использовать большее число членов. Рассматриваемые далее ряды позволяют вычислить широту и долготу Луны с точностью до нескольких угловых минут, а расстояние до Луны — с точностью около 500 км. Расчет возмущений основывается на пяти фундаментальных аргументах: средней долготе Луны (L_0) , средней аномалии Луны (l) , средней аномалии Солнца (l^prime) , среднем угловом расстоянии Луны от восходящего узла (F) и разности (D) между средними долготами Солнца и Луны. Долгота восходящего узла (Omega) в явном виде не используется, ее получают из разности (Omega = L_0 — F) .
Фундаментальные аргументы вычисляются по формулам
Координаты Луны (lambda_M) , (beta_M) и (r_M) , относящиеся к среднему равноденствию и эклиптике в эпоху J2000, записываются следующим образом [1]
Сферические эклиптические координаты (ref) преобразуются в прямоугольные экваториальные координаты по формулам
Преобразование координат при переходе от инерциальной системы эпохи J2000 к экватору и равноденствию текущей эпохи (T_text) выполняется так же, как и для солнечных координат.
Итак, прямоугольные координаты Луны в геоцентрической экваториальной системе координат заданной эпохи вычисляются по формулам (ref), (ref) и (ref) с учетом поправки (ref).
Более точное определение положений Солнца и Луны
Для определения координат Солнца и Луны широко используются разложения в ряды, основанные на аналитических теориях Ньюкома и Брауна. Точность этих теорий, как правило, вполне приемлема при описании влияния гравитационного притяжения Солнца и Луны на движение низкоорбитальных спутников Земли. Однако при прогнозировании движения спутников на высоких околоземных орбитах, использование теорий Ньюкома и Брауна вносит значительные ошибки в вычисленные положения спутника [2]. Эти ошибки можно существенно уменьшить, если использовать для вычисления координат Луны и Солнца высокоточные эфемериды — таблицы вычисленных положений небесных объектов.
В настоящее время широко употребляются высокоточные эфемериды больших планет, Солнца и Луны DE430 и DE431, построенные в Лаборатории реактивного движения (JPL) NASA. Эти эфемериды получены численными методами и дают координаты в виде полиномов Чебышева в прямоугольной барицентрической системе координат с экватором Земли и равноденствием, относящимися к эпохе J2000. В настоящее время они являются основой «Astronomical Almanac». Эфемериды DE430 охватывают период от 1550 г. до 2650 г., DE431 — от 13201 г. до н. э. до 17191 г. н. э.
Эфемериды, построенные в JPL, можно найти на ftp-сервере лаборатории. Кроме того, на веб-сайте JPL доступна программа HORIZONS для онлайн-генерации эфемерид объектов Солнечной системы (в том числе: астероидов, комет, спутников планет и некоторых космических аппаратов).
Европейский стандарт моделей описания космической среды (ECSS-E-ST-10-04C, от 15.11.2008) предполагает использование более ранней версии эфемерид JPL: DE-405/LE-405 (LE означает: эфемериды Луны — «Lunar Ephemerides»).
Эффекты общей теории относительности
Собственное гравитационное поле тела, вообще говоря, влияет на метрику пространства в окрестности этого тела. Собственное гравитационное поле современных спутников практически не оказывает влияния на движение массивных тел, а также на метрику пространства. Тем не менее, соответствующие поправки к правым частям уравнений движения описаны в [1].
Модели гравитационного поля Земли
В настоящее время Международный центр глобальных моделей гравитационного поля (International Center for Global Gravity Field Models) насчитывает 157 моделей гравитационного поля Земли. Наиболее современные из них можно получить на веб-сайте этой организации.
Одной из наиболее распространенных моделей является Earth Gravity Model 2008 (EGM2008), содержащая сферические гармоники до 2159 степени и порядка включительно (существует расширенная версия — вплоть до гармоник 2190 степени и 2159 порядка). Она разработана Национальным управлением геопространственной разведки США и используется Международной службой вращения Земли (IERS Conventions, 2010).
Европейский стандарт моделей космической среды ECSS-E-ST-10-04C предполагает использование модели EIGEN-GL04C, разработчиками которой являются исследовательские центры из Потсдама (GFZ Potsdam) и Тулузы (GRGS Toulouse).
Видео:Искусственные спутники Земли | Физика 9 класс #19 | ИнфоурокСкачать

Модели сил негравитационной природы
Сопротивление атмосферы
Среди сил негравитационной природы наибольшее воздействие на движение низкоорбитальных спутников (т. е. спутников, движущихся на высотах от 150 до 1500 км) оказывают аэродинамические силы, вызванные влиянием атмосферы Земли. Действие этих сил преимущественно выражается в сопротивлении движению спутника, направленном противоположно его скорости (vec_r) относительно атмосферы.
Рассмотрим малый элемент атмосферы массой (Delta m) , сталкивающийся со спутником с площадью поперечного сечения (A) за промежуток времени (Delta t)
где (rho) — плотность атмосферы в месте расположения спутника;
Импульс (Delta vec
) , испытываемый спутником, при этом равен
$$ Delta vec
= Delta m vec_r = rho A v^2_r Delta t cdot frac<vec_r>, $$
а соответствующая сила (vec) определяется из соотношения (vec = Delta vec
/ Delta t) . В результате, ускорение спутника, обусловленное сопротивлением атмосферы равно
где (C_D) — коэффициент сопротивления;
(m) — масса спутника;
Коэффициент сопротивления (C_D) представляет собой безразмерную величину, которая описывает взаимодействие атмосферы с материалом поверхности спутника. Обычно, значения (C_D) лежат в диапазоне от 1,5 до 3. Направление ускорения противоположно скорости движения спутника относительно атмосферы (vec_v) . Последняя зависит от сложной динамики атмосферы. Тем не менее, во многих практических случаях разумным приближением будет считать атмосферу вращающейся со скоростью вращения Земли. Следовательно, для (vec_r) можно записать
где (vec) и (vec) — положение и скорость спутника в инерциальной СК;
(vecg_oplus) — вектор угловой скорости вращения Земли ( (omega_oplus = 0,7292 cdot 10^) рад/c).
Плотность атмосферы (rho) является сложной функцией времени и геофизических параметров, зависящих от активности Солнца. Существует ряд моделей плотности.
Экспоненциальная атмосфера
Эта простейшая модель предполагает, что плотность атмосферы экспоненциально убывает с увеличением высоты (см., в частности, ГОСТ 4401-81)
где (rho_0) — плотность атмосферы на поверхности земного референц-эллипсоида, то есть приближения формы поверхности Земли эллипсоидом вращения ( (rho_0 = 1,225) кг/м (^3) при температуре (15^) C);
(h) — высота над поверхностью референц-эллипсоида (уровнем моря);
(H_0) — масштаб высоты по давлению, определяемый формулой
где (R) — универсальная газовая постоянная;
(M) — молярная масса сухого воздуха;
(T) — температура воздуха на уровне моря;
(g) — ускорение свободного падения.
Модель Харриса-Прейстера (Harris-Priester)
Эта модель, разработанная в начале 1960-х гг. [1], расширяет экспоненциальную модель, позволяя учесть суточные изменения плотности. Нагрев атмосферы солнечным излучением приводит к постепенному увеличению ее плотности — с освещенной стороны Земли возникает выпуклость, вершина которой (апекс) отстает приблизительно на 2 часа (или (30^circ) к востоку) от подсолнечной точки. Плотность атмосферы на заданной высоте в апексе (rho_m(h)) и противоположной ему относительно Земли точке (антапексе) (rho_M(h)) вычисляется с помощью экспоненциальной интерполяции между табулированными минимальным (rho_m(h_i)) и максимальным (rho_M(h_i)) значениями плотности на высотах (h_i)
где (h) — высота над поверхностью земного референц-эллипсоида.
Соответствующие масштабы высоты по давлению равны
Плотность атмосферы в заданной точке (rho(h)) выражается через (rho_m(h)) и (rho_M(h)) следующим образом
где (Psi) — угол между радиусом-вектором спутника (vec) и вершиной атмосферной выпуклости (апексом).
Широтные вариации атмосферы учитываются приблизительно, выбором показателя степени (n) , который для орбит с низким наклонением равен 2, а для приполярных орбит — 6.
Единичный вектор апекса (vec_a) задается как
где (alpha_odot) и (delta_odot) — прямое восхождение и склонение Солнца соответственно;
(lambda_l approx 30^circ) — угол запаздывания апекса относительно подсолнечной точки по долготе.
Значения (rho_m(h_i)) и (rho_M(h_i)) задаются таблично (см. [1]).
Современные модели атмосферы
Современными моделями плотности верхней атмосферы является модель ГОСТ Р 25645.166-2004 и модель NASA NRLMSISE-00. Обе они построены по результатам наблюдений со спутников и геофизических ракет и рассчитаны на применение в диапазоне высот от 120 до 1500 км над поверхностью Земли. Сравнительный анализ этих моделей (см. [2]) показал, что по своим возможностям они весьма близки.
Европейский стандарт моделей описания космической среды ECSS-E-ST-10-04C предполагает использование для плотности верхней атмосферы моделей NASA NRLMSISE-00 и Jacchia-Bowman 2006 (JB-2006). Последняя подробно описана в [3].
Солнечное давление
Для определения ускорения, вызванного давлением солнечного излучения, необходимо найти выражение для соответствующих сил, действующих на полностью освещенный спутник, и выяснить условия его освещенности.
Солнечное давление определяется величиной падающего на спутник потока солнечного излучения
то есть энергией (Delta E) , проходящей через поверхность площадью (A) за промежуток времени (Delta t) .
Единичный фотон с энергией (E_nu) переносит импульс
где (c) — скорость света.
Следовательно, полный импульс, переданный освещенному телу за время (Delta t) , равен
Таким образом, величина силы, действующей на спутник, равна
Соответственно, давление равно
Поток солнечной энергии на расстоянии 1 а. е. от Солнца (астрономическая единица приблизительно равна среднему расстоянию от Земли до Солнца: 1 а. е. = 149597870,691 км) равен
Следовательно, согласно (ref), давление солнечного излучения на орбите Земли равно
При этом предполагается, что спутник расположен перпендикулярно потоку излучения и поглощает все падающие на него лучи.
На практике, часть излучения отражается от поверхности спутника. Доля энергии отраженного излучения характеризуется коэффициентом отражения (epsilon) ( (epsilon=1) в случае полного отражения и (epsilon=0) — для полного поглощения).
Взаимодействие потока излучения с произвольно ориентированной плоской поверхностью для случаев полного поглощения и отражения показано на рис., где (vec) — вектор нормали, определяющий ориентацию поверхности площадью (A) , (vec_odot) — единичный вектор, указывающий направление на Солнце, (theta) — угол между (vec) и (vec_odot) .
Сила, действующая на поверхность, полностью поглощающую падающее излучение, равна
где (costheta A) — площадь поверхности, перпендикулярная потоку излучения.
В свою очередь сила, действующая на полностью отражающую поверхность, равна
Как видно из рис., импульс (Delta vec
_n) , передаваемый поверхности в направлении нормали, в случае полного отражения в два раза больше, чем в случае полного поглощения.
Изменение импульса в направлении нормали к поверхности (Delta vec
_n) : a) полное поглощение, б) полное отражение
Для тела, отражающего часть энергии (epsilon Delta E) и поглощающего оставшуюся часть ((1-epsilon) Delta E) , выражение для силы солнечного давления представляет собой комбинацию (ref) и (ref)
Наконец, учитывая, что поток солнечного излучения убывает пропорционально квадрату расстояния от Солнца, запишем ускорение спутника, вызванное солнечным давлением
где (m) — масса спутника;
(costheta = vec cdot vec_odot) ;
(nu) — функция тени, которую мы определим ниже.
Эллиптичность орбиты Земли приводит к тому, что расстояние между спутником, находящимся на околоземной орбите, и Солнцем изменяется в течение года в диапазоне от (147cdot 10^6) км до (152cdot 10^6) км. Это приводит к годичным вариациям солнечного давления в пределах (pm3,3) %.
Во многих случаях (например, для спутников с большими панелями солнечных батарей) для оценки сил солнечного давления достаточно предположить что нормаль к поверхности (vec) совпадает с направлением на Солнце. Тогда выражение (ref) упрощается до
где (C_R) — коэффициент солнечного давления.
Функция тени (nu) характеризует условия освещенности спутника Солнцем и принимает значения в диапазоне от 0 до 1 ( (nu=1) соответствует освещенному спутнику; (nu=0) — спутнику, находящемуся в тени; значения (0 соответствуют нахождению спутника в области полутени).
Простейшую функцию тени получим, предположив, что спутник может быть либо полностью освещен Солнцем, либо скрыт от него в тени планеты. Обозначим через (s) проекцию радиуса-вектора спутника (vec) на направление (vec_odot) . Тогда спутник освещен, если он находится между Солнцем и планетой или «позади» планеты, но не закрыт ею от Солнца (рис.). Этот результат можно записать в виде следующей функции
где (s = (veccdotvec_odot)) ;
Для более точных расчетов необходимо учесть попадание спутника в область полутени. Значения (nu) в этом случае зависят от степени перекрытия Солнца затеняющим телом (Землей или Луной). Рассмотрим модель в которой Солнце и затеняющее тело представлены круговыми дисками. Схема затенения Солнца сферическим телом показана на рис..
Согласно ей, видимый радиус Солнца (a) равен
где (R_odot) — радиус Солнца (см. пояснения на рис.).
Видимый радиус затеняющего тела (b) равен
где (R_B) — радиус затеняющего тела;
(vec = vec-vec_B) , (vec_B) — геоцентрический радиус-вектор центра затеняющего тела, (s = |vec|) — расстояние между спутником и затеняющим телом.
— видимое расстояние между центрами Солнца и затеняющего тела.
Тогда площадь перекрытого участка солнечного диска равна
Вычислив аналогично остальные площади из (ref), получим в результате
Доля незатененной части Солнца равна
Если условие (ref) не выполняется, то реализуется одна из следующих возможностей:
- затенения не происходит (при (a+b leq c) );
- затенение будет полным (когда (c при (a );
- затенение будет частичным, но максимально возможным (когда (c при (a>b) ).
Давление излучения Земли
Помимо давления солнечного излучения, на спутник действует также давление от излучения, испускаемого Землей. В этом излучении выделяют две составляющие: коротковолновое оптическое излучение и длинноволновое инфракрасное излучение. Возмущающее ускорение от излучения Земли постепенно уменьшается с увеличением высоты полета. С одной стороны, поток излучения подчиняется закону обратных квадратов, то есть убывает с высотой. С другой стороны, уменьшение потока частично компенсируется тем, что с увеличением высоты растет площадь поверхности Земли, освещающей спутник. Амплитуда типичного альбедо-ускорения для спутников на низких околоземных орбитах составляет от 10% до 35% от ускорения, вызываемого давлением непосредственно солнечного излучения [1].
Видео:Физика 9 класс (Урок№6 - Движение искусственных спутников Земли. Гравитация и Вселенная.)Скачать

Программное обеспечение расчета орбитального движения спутника
Подавляющее большинство из рассмотренных выше моделей внешних сил, действующих на орбитальное движение спутника, распространяется свободно в виде исходного кода библиотек, реализованных на языках Fortran или C. Подобный принцип распространения программного обеспечения представляется особенно важным в научных исследованиях, так как делает исходный код программ, являющихся составной частью работы, доступным для независимой проверки.
Рассмотрим программное обеспечение расчета орбитального движения космических аппаратов, которое распространяется свободно и с открытым исходным кодом.
GMAT (General Mission Analysis Tool) разрабатывается коллективом сотрудников Центра им. Годдарда NASA и группой частных компаний. Он предназначен для моделирования, анализа и оптимизации траекторий космических аппаратов в различных режимах полета, начиная с низких околоземных орбит и движения вокруг Луны и заканчивая межпланетными траекториями и другими дальними космическими полетами.
Анализ предстоящего полета в GMAT начинается с создания ресурсов (resources), таких как: космический корабль, пропагатор (propagator, то есть метод расчета орбиты), оптимизатор (optimizer, способ оптимизации орбиты) и т. п. Параметры ресурсов задаются в зависимости от задач полета. Так, можно указать типы и количество реактивных двигателей, объем баков с горючим, вид горючего и мн. др.
Помимо расчетов GMAT выполняет и визуализацию движения космического аппарата. Например, он позволяет отобразить траекторию подспутниковой точки на любой планете или другом небесном теле из доступных в программе. GMAT позволяет выводить двумерные графики, создавать анимацию, а также интерактивную трехмерную графику.
Помимо графического пользовательского интерфейса GMAT обладает собственным интерпретируемым языком программирования, который дает возможность работать с массивами и строками, создавать пользовательские функции и т. п. Поддерживаются интерфейсы прикладного программирования с Matlab и Python.
Orekit (ORbits Extrapolation KIT) — низкоуровневая библиотека для решения задач динамики космического полета.
Orekit предназначен для создания точных и эффективных низкоуровневых компонентов, используемых в программных приложениях из области динамики космического полета. Разработчики стремились сделать из него набор «строительных блоков», который можно было бы легко использовать в самых разных ситуациях — от простых оценочных расчетов, до анализа межпланетных перелетов. Библиотека используется в Национальном центре космических исследований (CNES, Франция).
Код Orekit написан на Java, и зависит только от наличия Java Standard Edition и математической библиотеки Hipparchus.
Scilab — это пакет прикладных программ для научных и инженерных расчетов, представляющий собой наиболее полную общедоступную альтернативу проприетарному пакету MATLAB. В состав пакета входит Xcos — инструмент для создания блочных моделей, аналог Simulink из пакета MATLAB. Scilab разработан в INRIA (Франция) и в настоящее время развивается консорциумом Scilab Consortium.
Scilab поддерживает несколько десятков пакетов-расширений (toolboxes), которые можно загрузить из репозитория ATOMS (AuTomatic mOdules Management for Scilab). Среди них, для расчета орбитального движения космического аппарата предназначены CelestLab (разработки CNES) и Aerospace Blockset — набор блоков для Xcos, основанных на CelestLab. Общим недостатком этих расширений является то, что в них используются лишь простейшие модели плотности атмосферы. Одним из способов решения этой проблемы является использование моделей, имеющихся в библиотеке Orekit (использовать Java-объекты в Scilab можно, установив расширение JIMS).
Видео:Всё об орбитальной механике | Как запускают спутникиСкачать

3. ОРБИТЫ ИСКУССТВЕННЫХ СПУТНИКОВ ЗЕМЛИ.
ОРБИТЫ ИСКУССТВЕННЫХ СПУТНИКОВ ЗЕМЛИ. ВЫВОД СПУТНИКОВ НА ОРБИТУ
Траектория движения ИСЗ называется орбитой. Во время свободного полета спутника, когда его бортовые реактивные двигатели выключены, движение происходит под воздействием гравитационных сил и по инерции, причем главной силой является притяжение Земли.
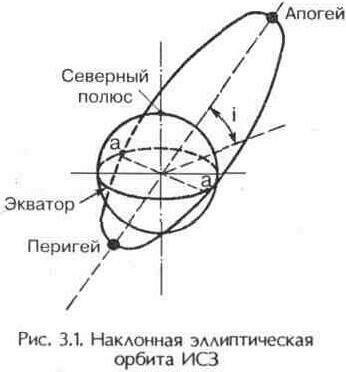
Если считать Землю строго сферической, а действие гравитационного поля Земли — единственной силой, воздействующей на спутник, то движение ИСЗ подчиняется известным законам Кеплера: оно происходит в неподвижной (в абсолютном пространстве) плоскости, проходящей через центр Земли, — плоскости орбиты; орбита имеет форму эллипса (рис 3.1) или окружности (частный случай эллипса).
При движении спутника полная механическая энергия (кинетическая и потенциальная) остается неизменной, вследствие чего при удалении спутника от Земли скорость его движения уменьшается.
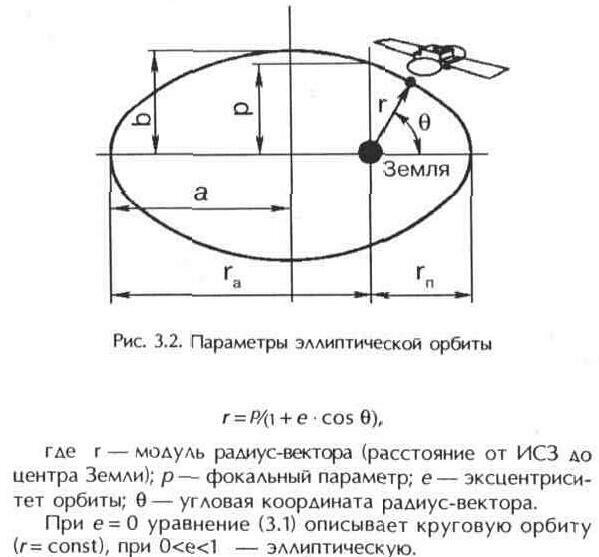
Уравнение эллиптической орбиты спутника Земли в полярной системе координат определяется формулой
В случае эллиптической орбиты точкой перигея называют точку орбиты, соответствующую наименьшему значению радиус-вектора r = rп, точкой апогея — точку, соответствующую наибольшему значению r = ra (рис. 3.2).
Земля находится в одном из фокусов эллипса. Входящие в формулу (3.1) величины связаны соотношениями:
Расстояние между фокусами и центром эллипса составляет ае, т. е. пропорционально эксцентриситету. Высота спутника над поверхностью Земли
где R — радиус Земли. Линия пересечения плоскости орбиты с плоскостью экватора (а — а на рис. 3.1) называется линией узлов, угол i между плоскостью орбиты и плоскостью экватора — наклонением орбиты. По наклонению различают экваториальные (i = 0°), полярные (i = 90°) и наклонные орбиты,(0°
Наблюдение искусственных спутников Земли
Видео:Ирина Пономарева — Орбитальная механика: уравнения движения в центральном полеСкачать  Глава 1: Как движутся ИСЗ?Перед тем, как приступить к рассмотрению вопросов наблюдения ИСЗ, нужно выяснить как они движутся — по каким орбитам и каковы характеристики этих орбит. Без понимания этих вопросов наблюдение ИСЗ превращается в охоту за неведомым зверем, который неизвестно где обитает. Видео:Основы орбитальной механики | Как в космосе летают спутникиСкачать  § 1. Законы Кеплера и типы орбитИз курса средней школы нам известно, что тело, движущееся по орбите вокруг другого тела, подчинено трём законам Кеплера. Нас будут интересовать только два из них — первый и третий. Согласно первому закону Кеплера, тело, обращающееся вокруг Земли (в нашем случае) движется по эллипсу, в одном из фокусов которого находится центр Земли (см. рис. 2). Мы специально не упоминали тут, что тело может двигаться по трём видам орбит — эллипс, гипербола и парабола. Нас интересуют только периодические орбиты, а из перечисленных такой является эллипс.
Элементы эллипса показаны на рис. 2. «F1« и «F2« — фокусы эллипса; «a» — большая полуось; «b» — малая полуось; «е» — эксцентриситет эллипса, который определяется следующим образом:
Таким образом, первое важное положение — ИСЗ движутся вокруг Земли по эллипсам . Согласно третьему закону Кеплера, квадраты периодов обращения «T» спутников относятся как кубы их больших полуосей «a»:
Видео:Искусственные спутники Земли. История развитияСкачать  § 2. Орбитальные элементыДля того, чтобы задать параметры и ориентацию орбиты ИСЗ в пространстве, нужно указать 6 т.н. кеплеровских элементов (орбитальных элементов) (см. рис. 3):
Итак, наше второе важное положение — орбита ИСЗ полностью задаётся шестью орбитальными элементами . Видео:9 класс. Движение искусственных спутников Земли. Практическая работаСкачать  § 3. Круговая орбитаРассмотрим частный случай эллиптической орбиты — круговая орбита. Если значение эксцентриситета орбиты ИСЗ е = 0, то орбита представляет собой окружность с центром в центре Земли. Для того, чтобы тело стало спутником Земли, оно должно обладать определённой скоростью при полёте вокруг неё. Если бы у Земли не было атмосферы, то минимальная скорость, необходимая для того, чтобы тело двигалось по окружности вокруг Земли, равна vк0 = 7,91 км/с. Но в реальности такого быть не может — спутник будет сильно тормозится в атмосфере Земли. Если ИСЗ начнёт двигаться на высоте менее примерно 160 км от поверхности Земли, то он сможет сделать лишь пару оборотов, после чего начнёт необратимо терять скорость и сгорит в плотных слоях атмосферы. Для примерного расчёта скорости ИСЗ на круговой орбите можно воспользоваться формулой [1]:
где R = 6371 км — средний радиус Земли, r = R + h — расстояние от центра Земли до ИСЗ, h — высота ИСЗ над поверхностью Земли. При наблюдениях важно знать период обращения ИСЗ Т — время, необходимое на один полный оборот вокруг Земли. Для круговой орбиты период Т можно вычислить по формуле [1]:
Из (4) видно, что минимальное время, необходимое ИСЗ для одного оборота, равно Tк0 = 84,4 минуты — при нулевой высоте над поверхностью. Никакое тело не может быстрее обогнуть поверхность Земли. При примерных оценках периода обращения ИСЗ по круговой орбите полезно помнить, что период обращения увеличивается примерно на 1 минуту при увеличении высоты ИСЗ на каждый 50 км. Этой оценкой можно пользоваться для ИСЗ не выше 1000 км. Наше третье важное положение — ИСЗ не может двигаться долгое время по орбите вокруг Земли ниже 140-160 км. При этом, период обращения по круговой орбите является минимальным и для диапазона высот 160-1000 км изменяется всего с 87,6 до 105 минут . Видео:Вращение Земли вокруг СолнцаСкачать  § 4. Эллиптическая орбитаТеперь рассмотрим общий вид орбиты ИСЗ — эллиптическая орбита (см. рис. 4). Как было указано выше, из первого закона Кеплера следует, что в фокусе эллиптической орбиты будет находится Земля (З), вокруг которой вращается ИСЗ. Двигаясь по эллиптической орбите, ИСЗ ближе всего подлетает к центру Земли в точке «П» — в перигее, а дальше всего находится в точке «А» — в апогее. Линия, соединяющая перигей и апогей называется линией апсид. Из наблюдений ИСЗ можно определить большую полуось и эксцентриситет орбиты, из которых можно вычислить значения перигейного «q» и апогейного «Q» расстояний:
Из (5) видно, что Q + q = 2a. При движении по орбите изменяется расстояние «r» от Земли до ИСЗ — величина радиус-вектора «r» задаётся выражением [3]:
Скорость ИСЗ в любой точке эллиптической орбиты задаётся выражением [2]:
Период обращения для спутника на эллиптической орбите вычисляется по формуле (4), в которой вместо «r» нужно подставить значение большой полуоси «a». Наше четвёртое важное положение — скорость движения ИСЗ по эллиптической орбите не равномерна: максимальна она в перигее, а минимальна в апогее. Период обращения теперь определяется не только большой полуосью «a», но и значением эксцентриситета «e» . Видео:ФИЗИКА 10 класс: Период движения спутника | ВидеоурокСкачать  § 5. Эволюция орбиты ИСЗВ этом параграфе мы рассмотрим, как изменяются параметры реальной орбиты ИСЗ под воздействием определённых факторов. Прежде всего следует отметить следующее: если бы Земля имела форму идеального шара с равномерным распределением вещества, была лишена атмосферы, а Луна и Солнце отсутствовали бы, то ИСЗ вечно бы вращался по своей орбите, ориентация которой в пространстве не изменялась. Если бы спутник совершал 14 оборотов в сутки (при этом его период равен примерно 103 минуты), то за время одного витка ИСЗ Земля повернётся на 1/14 полного оборота (это примерно 26°). Это означает, что с каждым новым траектория ИСЗ смещалась к западу на 26° за каждый виток. Прецессия орбитыВ реальности форма Земли — геоид, полярный радиус которого RП = 6356,8 км, а экваториальный — RЭ = 6378,2 км, т.е. экваториальный радиус больше полярного на 21,4 км. Земля имеет экваториальный «горб», который своей массой оказывает влияние на движение ИСЗ. Влияние это не такое уж явное — масса «горба» не вызывает изменения наклонения «i» орбиты за счёт притягивания плоскости орбиты к плоскости экватора, как можно было бы ожидать — плоскость орбиты медленно поворачивается вокруг земной оси в направлении, противоположном вращению ИСЗ (см. рис. 5).
Этот процесс называется прецессией. Угол прецессии плоскости орбиты ИСЗ остаётся неизменным. Угловая скорость прецессии «X1« (градусов в сутки) определяется, в основном, наклонением орбиты [1]:
где «i» — наклонение орбиты, «e» — эксцентриситет, RЭ — экваториальный радиус Земли, «а» — большая полуось орбиты ИСЗ. Если спутник движется в запада на восток, орбита поворачивается с востока на запад. Чем меньше наклонение ИСЗ, тем больше значение прецессии (см. рис. 6). Если спутник вращается с востока на запад (обратное движение ИСЗ), то прецессия орбиты происходит в обратную сторону. При этом линия узлов также поворачивается (см. рис. 7).
Теперь посмотрим, к каким изменениям условий наблюдения спутника приводит прецессия. Как известно, Земля делает полный оборот за 23 ч 56 м 4,09 с (звёздные сутки) — за 24 ч (средне-солнечные сутки) небо нам кажется повернувшимся на 361° (т.к. звёздные сутки короче средне-солнечных на 4 минуты — за это время небо повернётся на 1°). Если бы плоскость орбиты ИСЗ не прецессировала, то через 24 ч он появлялся бы на небе на 1° западнее, чем накануне (если движение ИСЗ прямое). Но за счёт прецессии орбита поворачивается на Х1 градусов за сутки, поэтому ИСЗ через 24 ч окажется на Х1 + 1 градус западнее (при обратном движении — на 1 — Х1 градус к западу). Период обращения спутника не кратен целой части суток. Если через сутки спутник будет пересекать ту же широту Земли на n минут позже, он окажется ещё на n/4 градусов западнее, т.к. за 1 минуту Земля поворачивается на 1/4 минуты. Следовательно, суммарный суточный сдвиг к западу составит (Х1 + 1 + n/4) градусов [1]. Вращение эллиптической орбитыСледующим важным эффектом, влияющим на эволюцию орбиты ИСЗ, является поворот плоскости эллиптической орбиты. Эффект этот, как и предыдущий, обязан своим существованием экваториальному «горбу» Земли, но в отличие от прецессии, действует только на эллиптичные орбиты. Эффект заключается в том, что эллиптическая орбита постоянно поворачивается в своей плоскости вперёд для спутников с нулевым наклонением, и назад — для спутников с наклонением, близким к 90°. За счёт этого точки перигея движутся вперёд или назад по орбите (см. рис. 8).
Скорость вращения «X2« эллиптической орбиты определяется выражением [1]:
На рис. 9 показаны графики зависимости X2(i) для ИСЗ с разными значениями больших полуосей «a».
Вращение происходит в том же направлении, что и движение спутника, если наклонение i 63,4°. При i = 63,4° поворот орбиты отсутствует. Наше пятое важное положение — движение ИСЗ подвержено возмущениям из-за несферичности Земли. За счёт прецессии орбита спутника может смещаться с угловой скоростью до 9°/сутки, а за счёт поворота эллиптической орбиты — до 15°/сутки. При этом, чем меньше наклонение, тем сильнее оба эффекта, но действовать они могут как в одну сторону, так и в противоположные . Атмосферное торможениеПрецессия орбиты и поворот её плоскости связаны с действием несферичности Земли. Но кроме этого Земля окружена атмосферой, которая прослеживается до 2000 км над её поверхностью. Из этого следует, что на движение ИСЗ, особенно на низких орбитах, влиянием атмосферы мы пренебрегать не можем. Атмосферное давление падает с высотой экспоненциально — на высоте 200 км оно составляет 10 -12 мбар (на уровне моря атмосферное давление составляет 1013 мбар), а на высоте 900 км — уже только 10 -42 мбар [6]. Тем не менее, даже такая разреженная атмосфера может приводить к изменению орбиты ИСЗ. Сила сопротивления движущемуся в атмосфере телу определяется выражением [4]:
где «cx« — безразмерный коэффициент сопротивления, для верхней атмосферы равный 2-2,5; «S» — площадь максимального сечения спутника, перпендикулярного налетающему воздушному потоку; «v» — скорость ИСЗ, «ρ» — плотность атмосферы на высоте полёта ИСЗ. Торможение ИСЗ определяется его парусностью — чем больше площадь и меньше масса, тем больше торможение. Для спутника, движущемся по круговой орбите, сопротивление атмосферы будет сказываться следующим образом: спутник будет медленно опускаться по спирали с постоянно увеличивающейся скоростью. Угол снижения спутника на круговой орбите можно оценить из выражения [1]:
где «m» — масса ИСЗ, «g» — ускорение свободного падения. Снижение по спирали будет продолжаться до тех пор, пока спутник не опустится до высоты 160 км — ниже этой высоты сила сопротивления настолько велика, что спутник начинает резкое снижение и сгорит в атмосфере. На высоте 160 км период обращения равен примерно 88 минут — любой ИСЗ с меньшим периодом обречён. Если орбита эллиптическая, то результат действия сопротивления атмосферы будет следующим: т.к. сопротивление сильно уменьшается с высотой, то максимальное сопротивление ИСЗ будет испытывать в перигее, а минимальное — в апогее. Это слабо меняет высоту перигея, но уменьшает высоту апогея — в результате эллиптичность орбиты уменьшается и спутник начинает спуск по спирали. На рис. 10 показано снижение ИСЗ в случае эллиптической орбиты.
Оценить время жизни спутника можно из выражения (12) [1]:
где e0 — начальный эксцентриситет орбиты, T0 — начальный период обращения, ΔT — суточное изменение периода. Тогда измение периода будет определятся выражением [1]:
а изменение эксцентриситета [1]:
Формулы (13) и (14) справедливы для значений e = 0,02-0,2. На атмосферное торможение сильно влияет время суток (в подсолнечной точке атмосфера подымается выше), а также активность Солнца. Как видно, время жизни спутника определяется его эксцентриситетом и большой полуосью. В таблице ниже представлены времена жизни ИСЗ для разных значений перигея и апогея [5]:
Наше шестое важное положение — сопротивление атмосферы Земли вызывает уменьшение большой полуоси орбиты ИСЗ, в результате чего он по спирали спускается вниз. При достижении высоты около 160 км спутник сможет сделать всего пару оборотов и сгорит в атмосфере, войдя в резкий и необратимый спуск . Давление светаВпервые идею о том, что свет производит давление на тела, высказал в 1619 г. И. Кеплер — для объяснения эффекта отклонения кометных хвостов от Солнца. Современная теория даёт значение давления следующим выражением (формула Максвелла-Бартоли) [3]: где «E» — мощность электромагнитного излучения, приходящаяся на единицу площади тела, «η» — коэффициент отражения тела, «c» — скорость света. Для абсолютно поглощающего тела вблизи Земли давление света равно 4,3 · 10 -6 Н/м 2 . Для абсолютно отражающего тела эта величина в два раза больше. Световое давление становится ощутимым для лёгких спутников выше 500 км, т.к. ниже большее значение имеют колебания плотности атмосферы. В заключении параграфа нужно отметить, что перечисленные факторы влияния на эволюцию орбиты спутника не составляют полный список. Например, на ИСЗ воздействуют своим притяжением Солнце и Луна, но это воздействие в 10000 раз слабее действия экваториального «горба» Земли, но его нужно учитывать для орбит с большим эксцентриситетом. Экваториальный «горб» также вызывает незначительные колебания плоскости орбиты ИСЗ при пересечении экваториальной плоскости. Наконец, неравномерность распределения масс под поверхностью Земли также сказывается на движении спутника. Как видим, движение спутника не так просто, как может показаться на первый взгляд. В наше время расчёты эволюции орбиты значительно упростились с точки зрения затраты времени, т.к. современные компьютеры имеют огромную вычислительную мощность. Даже любители, используя специальные программы (см. далее), могут довольно точно расчитывать положение спутников на нужную им дату и время, причём на любой промежуток времени — в начале космической эры любители могли об этом только мечтать. 🎦 ВидеоКак собирают и запускают в космос спутники связиСкачать  Физика Для связи используют искусственный спутник Земли, «висящий» постоянно над одной и той жеСкачать  Законы КеплераСкачать  Движение искусственных спутников земли. Расчёт первой космической скоростиСкачать  Урок 65. Движение планет. Законы КеплераСкачать  Физика Два одинаковых спутника обращаются вокруг Земли по круговым орбитам, радиусы которых в 2 и 4Скачать  Vsauce: как движется ЗемляСкачать  ЕГЭ по физике. Теория #13. Движение спутниковСкачать  Как на самом деле движутся планеты Солнечной системы?Скачать  Геостационарные спутникиСкачать  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||







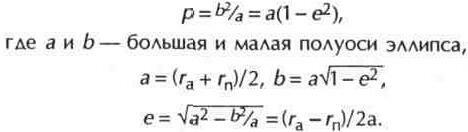

 ,     (1)
,     (1)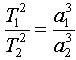 ,     (2)
,     (2)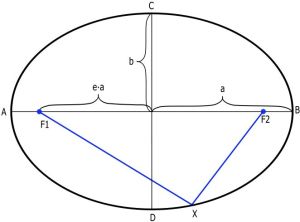

 ,     (3)
,     (3) ,     (4)
,     (4) .     (5)
.     (5)
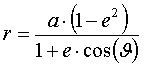 .     (6)
.     (6)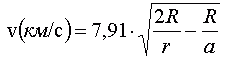 .     (7)
.     (7)
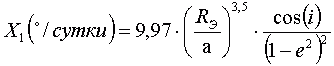 ,     (8)
,     (8)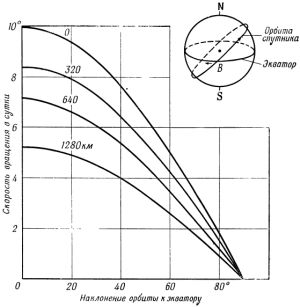


 .     (9)
.     (9)
 ,     (10)
,     (10)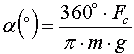 ,     (11)
,     (11)
 ,     (12)
,     (12) ,     (13)
,     (13) .     (14)
.     (14)