Уравнение движения шкива в машине атвуда

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Экспериментальная проверка основных уравнений и законов поступательного движения тела в поле сил земного тяготения, определение ускорения свободного падения лабораторной установке – машине Атвуда.

Машина Атвуда (рис.1) состоит из легкого блока 2, через который переброшена нить с двумя наборными грузами на концах (массы обоих грузов одинаковы и равны m ). Грузы могут двигаться вдоль вертикальной рейки со шкалой 1. Если на правый груз положить небольшой перегрузок D m , грузы начнут двигаться с некоторым ускорением. Для приема падающего груза служит полочка 3.

Видео:Пример 1. Задача "Машина Атвуда"Скачать

Время движения грузов измеряется с помощью ручного или стационарного секундомера.

Силы трения в машине Атвуда сведены к минимуму, но не равны нулю. Для возможно полной их компенсации масса одного из грузов (в нашей установке – правого) делается немного больше массы другого. Эта операция производится при помощи кусочков пластилина и выполняется с таким расчетом, чтобы а) грузы могли находиться в статическом положении сколь угодно долго, но б) от легкого толчка вниз правого груза вся система приходила в равномерное движение. Масса используемого пластилина столь мала, что в последующих расчетах в массу грузов не включается. Перегрузки D m , с помощью которых системе задается движение, укладывают также на правый груз системы.

Для выполнения работы машина Атвуда должна быть установлена строго вертикально, что легко проверить по параллельности шкалы и нити.

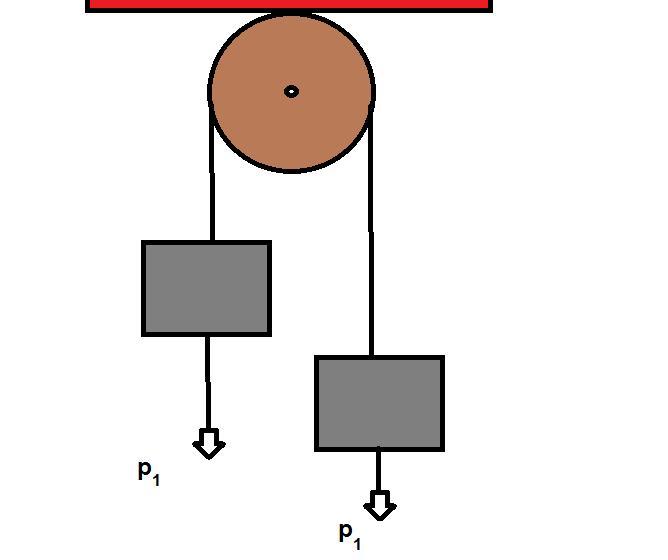
Второй закон Ньютона в проекциях на вертикальную ось для каждого из тел системы (рис.2) в предположении невесомости блока, отсутствия силы трения и нерастяжимости нити дает:

(1)

Где g — ускорение свободного падения,

a — ускорение грузов,

Выразим из данной системы ускорение a .

(2)

Проверим равноускоренный характер движения грузов, экспериментально получая значения пути данных грузов S (для обоих грузов он одинаков) и время движения t .

Видео:ФИЗИЧЕСКИЙ ПРАКТИКУМ: МАШИНА АТВУДАСкачать

Так как начальная скорость в опытах на машине Атвуда обычно равна нулю и движение условно начинается из начала координат, то

(3)

Третье соотношение часто называют законом перемещений: «Перемещение при равноускоренном движении прямо пропорционально квадрату времени движения».

Соотношение (3) может быть проверено экспериментально на машине Атвуда. Кроме того, машина Атвуда дает возможность экспериментально проверить второй закон Ньютона для поступательного движения: «Ускорение, с которым движется тело, прямо пропорционально равнодействующей действующих на него сил и обратно пропорционально массе этого тела».

Подставляя a _i в (2) получаем следующую формулу:

(4)

Для получения более точного значения g , необходимо учесть момент инерции блока — J _б, ( T ₁ T ₂). Рассмотрим получения вышеописанных формул с учётом новой величины. Вычислим g из закона динамики для вращательного движения тела (в данном случае блока).

(5)

— сумма проекций на ось Z всех сил, действующих на вращающиеся тело; α- угловое ускорение блока; J – его момент инерции

(6)

Где r — радиус блока, J _б — момент инерции блока.

Выразим из уравнения (1) разность сил натяжения ( T ₁ – T ₂ ) и подставив ее в уравнение (6) получим:

(7)

Выразим ускорение грузов a :

(8)

Учитывая, что значение момента инерции блока

(9),

k- коэффициент распределения массы блока относительно оси вращения (k

11)

Задание 1. Проверка второго закона Ньютона.

Поскольку ускорение движения является функцией двух переменных – силы и массы, то изучение второго закона Ньютона выполняется путем раздельного исследования двух зависимостей: 1) зависимости ускорения от действующей силы при постоянной массе системы и 2) зависимости ускорения от массы системы при постоянной действующей силе.

Исследование зависимости ускорения от силы при постоянной массе

Измерения и обработка результатов

1. Тщательно балансируют грузы, выбрав их массы в пределах 150 — 200 г каждый.

2. Затем на правый груз последовательно накладывают перегрузки. В результате в системе появляется движущая сила равная  mg, где  m — суммарная масса перегрузков. При этом, конечно, общая масса системы незначительно увеличивается, но этим изменением массы по сравнению с массой грузов можно пренебречь, считая массу системы постоянной.

3. Измеряют время равноускоренного движения системы на пути, например, 1 метр. Все данные заносят в таблицу 1.3 отчета.

4. Пользуясь законом путей (1.6), вычисляют ускорение а.

5. Поводят еще 5-6 опытов, последовательно увеличивая массу перегрузков.

6. Строят график зависимости ускорения движения от действующей силы. Точку ( F =0, a =0) на графике не откладывают. Если экспериментальные точки ложатся на прямую с небольшим разбросом и прямая проходит через начало координат, то можно сделать вывод о том, что ускорение действительно прямо пропорционально силе.

7. По угловому коэффициенту полученной прямой определяют массу системы и сравнивают ее реальной массой.

Исследование зависимости ускорения от массы при постоянной силе

Измерения и обработка результатов

1. Все опыты проводят с одним и тем же перегрузком, т.е. при постоянной действующей силе. Ускорение системы измеряется также как и в предыдущем задании.

2. Для изменения массы системы одновременно на правый и левый груз кладут дополнительные одинаковые грузы. Все данные записывают в таблицу отчета.

3. График обратно пропорциональной зависимости ускорения от массы представляет собой гиперболу, которую невозможно идентифицировать. Для проверки предположения об обратно пропорциональной зависимости между ускорением и массой необходимо построить график зависимости ускорения от обратного значения массы системы: a = f (М -1 ). Подтверждением предположения является прямолинейность этого графика.

4. По угловому коэффициенту полученной прямой определяют значение приложенной силы и сравнивают ее с реально действующей в системе

Задание 2. Определение ускорения движения грузов

В полученном уравнении прямой коэффициент k равен половине ускорения системы: k=a/2. Это позволяет вычислить ускорение грузов ( a =2 k ) в данном опыте и определить погрешность его измерения. Произведите необходимые вычисления и занесите результаты в отчет.

Задание 3. Определение ускорения свободного падения

(Выполняется по результатам измерений и вычислений, проведенных в первом и втором заданиях). Зная массы грузов и перегрузка, а также ускорение движения системы, из формулы (3) найдите ускорение свободного падения. Результаты занесите в отчет. В выводе сравните полученный результат с табличной величиной.

Для нахождения погрешности измерения величины ускорения свободного падения Δ g используем формулу:

12)

где ; ; ; ;

– частные производные функции

Проанализируйте результаты своих наблюдений и сформулируйте вывод.

Видео:Машина АтвудаСкачать

Контрольные вопросы

Какое движение называется поступательным?

Дайте определение инерциальной системы отсчета. Приведите примеры ИСО.

Сформулируйте первый закон Ньютона. Приведите примеры его проявления.

Дайте определение инертной массы тела. Гравитационной? От чего и как зависит масса тела?

Сформулируйте второй закон Ньютона. Приведите варианты его математической формы.

Покажите все силы, действующие на один из грузов в машине Атвуда, и составьте для него уравнение динамики.

Запишите систему уравнений динамики для машины Атвуда с учетом момента инерции блока. Силы трения в блоке?

Видео:Основное уравнение динамики вращательного движения. 10 класс.Скачать

Изучение законов поступательного движения на машине Атвуда: формулы и пояснения

Использование простых механизмов в физике позволяет изучать различные природные процессы и законы. Одним из этих механизмов является машина Атвуда. Рассмотрим в статье, что она собой представляет, для чего используется, и какие формулы описывают принцип ее работы.

Видео:Уравнение движенияСкачать

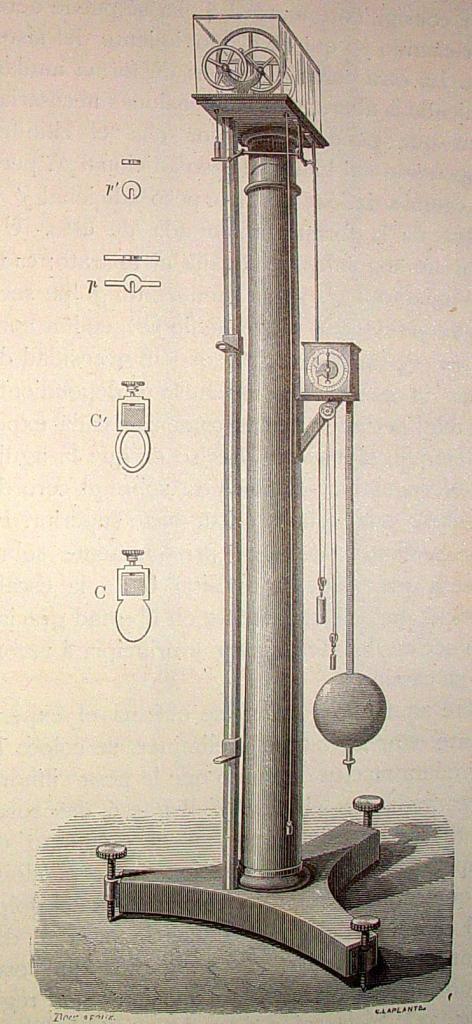
Что такое машина Атвуда?

Названная машина представляет собой простой механизм, состоящий из двух грузов, которые соединены переброшенной через неподвижный блок нитью (веревкой). В данном определении следует пояснить несколько нюансов. Во-первых, массы грузов в общем случае являются разными, что обеспечивает наличие у них ускорения под действием силы тяжести. Во-вторых, нить, связывающая грузы, считается невесомой и нерастяжимой. Эти предположения значительно облегчают последующие расчеты уравнений движения. Наконец, в-третьих, неподвижный блок, через который переброшена нить, также считается невесомым. Кроме того, во время его вращения пренебрегают силой трения. Ниже на схематическом рисунке показана эта машина.

Вам будет интересно: Пространственная экономика: описание специальностей и структура

Вам будет интересно: Что такое подполье? Подпольная организация «Молодая гвардия». Антифашистское движение

Машина Атвуда была изобретена английским физиком Джорджем Атвудом в конце XVIII века. Служит она для изучения законов поступательного движения, точного определения ускорения свободного падения и экспериментальной проверки второго закона Ньютона.

Видео:Машина АтвудаСкачать

Уравнения динамики

Каждый школьник знает, что ускорение у тел появляется только в том случае, если на них оказывают действие внешние силы. Данный факт был установлен Исааком Ньютоном в XVII веке. Ученый изложил его в следующем математическом виде:

Где m – инерционная масса тела, a – ускорение.

Изучение законов поступательного движения на машине Атвуда предполагает знание соответствующих уравнений динамики для нее. Предположим, что массы двух грузов равны m1 и m2, причем m1>m2. В таком случае первый груз будет перемещаться вниз под действием силы тяжести, а второй груз будет двигаться вверх под действием силы натяжения нити.

Рассмотрим, какие силы действуют на первый груз. Их две: сила тяжести F1 и сила натяжения нити T. Силы направлены в разных направлениях. Учитывая знак ускорения a, с которым перемещается груз, получаем следующее уравнение движения для него:

Что касается второго груза, то на него действуют силы той же природы, что и на первый. Поскольку второй груз движется с ускорением a, направленным вверх, то уравнение динамики для него принимает вид:

Таким образом, мы записали два уравнения, в которых содержатся две неизвестных величины (a и T). Это означает, что система имеет однозначное решение, которое будет получено далее в статье.

Видео:Машина Атвуда (ко 2-му закону Ньютона)Скачать

Расчет уравнений динамики для равноускоренного движения

Как мы видели из записанных выше уравнений, результирующая сила, действующая на каждый груз, остается неизменной в процессе всего движения. Масса каждого груза также не меняется. Это означает, что ускорение a будет постоянным. Такое движение называют равноускоренным.

Изучение равноускоренного движения на машине Атвуда заключается в определении этого ускорения. Запишем еще раз систему динамических уравнений:

Чтобы выразить значение ускорения a, сложим оба равенства, получаем:

F1 – F2 = a*(m1 + m2) =>

a = (F1 – F2)/(m1 + m2).

Подставляя явное значение сил тяжести для каждого груза, получаем конечную формулу для определения ускорения:

a = g*(m1 – m2)/(m1 + m2).

Отношение разницы масс к их сумме называют числом Атвуда. Обозначим его na, тогда получим:

Видео:Виртуальные лаборатории «Наука». Машина Атвуда. Обучающий ролик.Скачать

Проверка решения уравнений динамики

Выше мы определили формулу для ускорения машины Атвуда. Она является справедливой только в том случае, если справедлив сам закон Ньютона. Проверить этот факт можно на практике, если провести лабораторную работу по измерению некоторых величин.

Лабораторная работа с машиной Атвуда является достаточно простой. Суть ее заключается в следующем: как только грузы, находящиеся на одном уровне от поверхности, отпустили, необходимо засечь время движения грузов секундомером, а затем, измерить расстояние, на которое переместился любой из грузов. Предположим, что соответствующие время и расстояние равны t и h. Тогда можно записать кинематическое уравнение равноускоренного движения:

Откуда ускорение определяется однозначно:

Отметим, что для увеличения точности определения величины a, следует проводить несколько экспериментов по измерению hi и ti, где i – номер измерения. После вычисления значений ai, следует рассчитать среднюю величину acp из выражения:

Где m – количество измерений.

Приравнивая это равенство и полученное ранее, приходим к следующему выражению:

Если данное выражение оказывается справедливым, то таковым также будет и второй закон Ньютона.

Видео:Поступательное и вращательное движения.Скачать

Расчет силы тяжести

Выше мы предположили, что значение ускорения свободного падения g нам известно. Однако при помощи машины Атвуда определение силы тяжести также оказывается возможным. Для этого вместо ускорения a из уравнений динамики следует выразить величину g, имеем:

Чтобы найти g, следует знать, чему равно ускорение поступательного перемещения. В пункте выше мы уже показали, как его находить экспериментальным путем из уравнения кинематики. Подставляя формулу для a в равенство для g, имеем:

Вычислив значение g, несложно определить силу тяжести. Например, для первого груза ее величина будет равна:

Видео:ИЗУЧЕНИЕ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛАСкачать

Определение силы натяжения нити

Сила T натяжения нити является одним из неизвестных параметров системы динамических уравнений. Выпишем еще раз эти уравнения:

Если в каждом равенстве выразить a, и приравнять оба выражения, тогда получим:

(F1 – T)/m1 = (T – F2)/m2 =>

T = (m2*F1 + m1*F2)/(m1 + m2).

Подставляя явные значения сил тяжести грузов, приходим к конечной формуле для силы натяжения нити T:

T = 2*m1*m2*g/(m1 + m2).

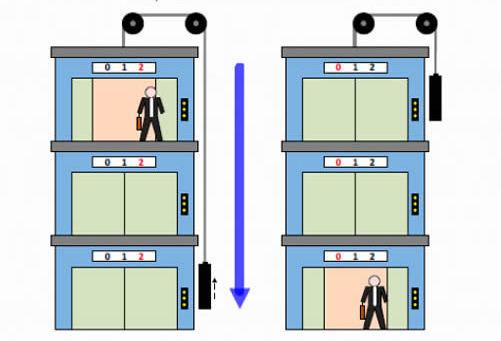
Машина Атвуда имеет не только теоретическую пользу. Так, подъемник (лифт) использует при своей работе контргруз с целью подъема на высоту полезного груза. Такая конструкция значительно облегчает работу двигателя.

Видео:Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

Изучение прямолинейного движения тел на машине Атвуда

Федеральное Агентство по образованию

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)

Лабораторная работа по курсу «Общая физика»

ИЗУЧЕНИЕ ПРЯМОЛИНЕЙНОГО ДВИЖЕНИЯ ТЕЛ

НА МАШИНЕ АТВУДА

Преподаватель Студент группы

___________ /____________. / / ____________ /

___________2010 г. __________ 2010 г.

Целью работы является изучение закона прямолинейного ускоренного движения тел под действием сил земного тяготения с помощью машины Атвуда.

2. ОПИСАНИЕ УСТАНОВКИ И МЕТОДИКИ ЭКСПЕРИМЕНТА

Схема экспериментальной установки на основе машины Атвуда приведена на рис.2.1.

На вертикальной стойке 1 крепится легкий блок 2, через который перекинута нить 3 с грузами 4 одинаковой массы. В верхней части стойки расположен электромагнит, который может удерживать блок, не давая ему вращаться. На среднем кронштейне 5 закреплен фотодатчик 6. На корпусе среднего кронштейна имеется риска, совпадающая с оптической осью фотодатчика. Средний кронштейн имеет возможность свободного перемещения и фиксации на вертикальной стойке. На вертикальной стойке укреплена миллиметровая линейка 7, по которой определяют начальное и конечное положения грузов. Начальное положение определяют по нижнему срезу груза, а конечное — по риске на корпусе среднего кронштейна.

Миллисекундомер 8 представляет собой прибор с цифровой индикацией времени. Регулировочные опоры 9 используют для регулировки положения экспериментальной установки на лабораторном столе.

Принцип работы машины Атвуда заключается в том, что когда на концах нити висят грузы одинаковой массы, то система находится в положении безразличного равновесия. Если на правый груз положить перегрузок, то система грузов выйдет из состояния равновесия и начнет двигаться.

3. ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ

Среднее значение времени прохождения системой некоторого расстояния S определяется согласно соотношения:

(3.1)

где – порядковый номер измерения времени, =1.. n , n – номер последнего измерения, количество измерений.

Аналогично для квадрата времени:

(3.2)

Случайная погрешность измерений:

(3.3)

г де – случайная погрешность измерения времени, – случайная погрешность измерения квадрата времени, – коэффициент Стьюдента, – количество значений, – доверительная вероятность, – средняя квадратичная погрешность среднего значения времени, – средняя квадратичная погрешность среднего значения квадрата времени.

Средние квадратические погрешности средней величины:

(3.4)

Согласно теории вероятности, если абсолютная погрешность некоторого измерения больше утроенной среднеквадратической погрешности, тогда такое измерение считается промахом и в дальнейшем исключается из обработки. Таким образом, необходимо чтобы для всех выбранных измерений соблюдалось условие:

(3.5)

Приборная погрешность измерения времени:

(3.6)

где – цена деления секундомера (в данной работе =0,001 с).

Общая погрешность измерений:

(3.7)

Относительная погрешность измерений:

(3.8)

Ускорение движения системы, согласно руководства по лабораторной работе, определим по формуле:

(3.9)

где и значения, определенные с помощью полученного графика линеаризованной зависимости .

Поскольку график зависимости теоретически должен проходить через начало системы координат, тогда для того, чтобы оценить погрешность вычисления ускорения движения системы необходимо для полученных данных найти такие две графические зависимости, для которых их угловой коэффициент (а это и есть, собственно, ускорение) был бы максимальным и минимальным. Большее из отклонений углового коэффициента от рассчитанного значения а и принимается как абсолютная погрешность Δа.

Относительная погрешность определения ускорения движения системы:

(3.10)

4. РЕЗУЛЬТАТЫ РАБОТЫ И ИХ АНАЛИЗ

Измеренные значения и результаты их обработки приведены в таблице.

Таблица 4.1 – Результаты прямых и косвенных измерений

= 6 , 32 см1/2

= 5 , 48 см1/2

=4, 47 см1/2

= 3 , 8 7, см1/2

= 3 ,1 6 , см1/2

Таблица 4.2 – Результаты первичного расчета погрешностей измерений

= 6 , 32 см1/2

= 5 , 48 см1/2

=4, 47 см1/2

= 3 , 8 7, см1/2

= 3 ,1 6 , см1/2

, c

, c2

, c

, c2

, c

, c2

, c

, c2

, c

, c2

, c

, c

, c2

, c2

Поскольку для всех полученных значений выполняется условие (3.5), тогда можно приступать к дальнейшей обработке результатов.

Исходя из того, что для каждого выбранного значения пути перемещения S было выполнено по n =5 измерений, тогда при доверительной вероятности α=0,95 коэффициент Стьюдента будет равен .

Таблица 4.5 – Результаты расчета погрешностей

= 6 , 32 см1/2

= 5 , 48 см1/2

=4, 47 см1/2

= 3 , 8 7, см1/2

= 3 ,1 6 , см1/2

, c

, c

, c

, c

, %

, c2

, c2

, c2

, c2

, %

Как видно из приведенных расчетов в данной лабораторной работе можно пренебречь приборной погрешностью вследствие её малости по сравнению со случайной погрешностью.

Согласно полученным данным построим графики зависимостей , , :

Согласно полученному графику линеаризованной зависимости , пользуясь формулой (3.9), получим:

(см/с2);

Для оценки абсолютной погрешности определения ускорения движения системы, мысленно проведем прямые, проходящие через начало координат системы и каждую экспериментально найденную точку зависимости и вычислим для каждой из них свой угловой коэффициент (3.9):

1) для прямой проходящей через точки (0;0) и (2,307; 3,16) угловой коэффициент равен 3,75 см/с2;

2) для прямой проходящей через точки (0;0) и (2,828; 3,87) угловой коэффициент равен 3,75 см/с2;

3) для прямой проходящей через точки (0;0) и (3,276; 4,47) угловой коэффициент равен 3,72 см/с2;

4) для прямой проходящей через точки (0;0) и (4,006; 5,48) угловой коэффициент равен 3,74 см/с2;

5) для прямой проходящей через точки (0;0) и (4,589; 6,32) угловой коэффициент равен 3,79 см/с2;

1) максимальный угловой коэффициент:

(см/с2);

2) минимальный угловой коэффициент:

(см/с2);

Соответственно получим отклонения:

(см/с2);

(см/с2);

В конечном итоге абсолютная погрешность определения углового ускорения движения системы:

см/с2;

(см/с2);

Относительная погрешность определения ускорения, согласно выражению (3.10):

;

В ходе данной лабораторной работы с помощью машины Атвуда был изучен закон прямолинейного равноускоренного движения тел под действием сил земного тяготения. В результате проведенных испытаний удалось получить графики зависимости перемещения от времени , перемещения от квадрата времени , корня квадратного от времени . Также в ходе выполнения работы было рассчитано ускорение движения системы (см/с2) с относительной погрешностью , что является отличным результатом. В заключение необходимо сказать, что поставленная цель работы была достигнута полностью, на что указывают относительные погрешности определения времени движения системы для различных перемещений (все менее 5%), а также допустимая точность определения искомого ускорения движения 2,4%.

6. ОТВЕТЫ НА КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какие силы действуют на груз с перегрузком во время движения?

На груз с перегрузком во время движения действуют сила земного тяготения и сила натяжения нити. Действием всех остальных сил в данной работе пренебрегаем (силы трения, сопротивления воздуха и т. д.)

2. Запишите уравнение движения для каждого из грузов.

Уравнение движения груза с перегрузком:

;

Уравнение движения груза без перегрузка:

;

где – масса каждого груза без перегрузка, – масса перегрузка, – ускорение свободного падения, и – силы натяжения нитей на грузе с перегрузком и грузе без перегрузка соответственно, и – ускорения движения грузов с перегрузком и без соответственно.

В силу не растяжимости нити ; при невесомом блоке .

3. Укажите возможные причины, обуславливающие несовпадение теоретических выводов с результатами измерений.

Среди причин, обуславливающих несовпадение теоретических выводов с результатами измерений можно назвать такие как: пренебрежение весом блока, пренебрежение силами трения и сопротивления в системе, пренебрежение весом, физическими и геометрическими свойствами нити, а также, что естественно, определенную погрешность вносят погрешности измерения всех величин.

4. Каким образом из линеаризованного графика можно оценить систематическую погрешность измерения времени?

Систематическая погрешность измерения времени может быть определена из линеаризованного графика зависимости по точке пересечения графика с координатной осью времени t .

5. Укажите физические допущения, используемые при теоретическом анализе движения грузов в машине Атвуда.

При теоретическом анализе движения грузов в машине Атвуда считается, что блок и нить невесомы, нить нерастяжима, силы трения малы; в силу чего допускается, что ускорение движения грузов и силы натяжения нити по разные стороны блока одинаковы.

К работе прилагается регистрационный файл (*. REG ).

📺 Видео

Урок 93. Основное уравнение динамики вращательного движенияСкачать

Уравнение движения тела дано в виде x=2−3t. ВычислиСкачать

Вращательное движение твёрдого тела. Задачи 1, 2, 3Скачать

Ременная передача. Урок №3Скачать

Урок 89 (осн). Задачи на вращательное движение - 1Скачать

Физика - уравнения равноускоренного движенияСкачать

Вращательное движение. 10 класс.Скачать

Момент инерцииСкачать

Поступательное и вращательное движенияСкачать