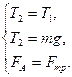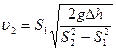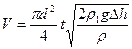Уравнение движения шарика в жидкости при постоянной скорости (8 видео)

Содержание

Рассмотрим падение шарика в вязкой жидкости
Ламинарное движение шарика в жидкости. Формула Стокса
Движение тел в вязкой среде. Закон Стокса.
🔍 Видео

Видео:Определение коэффициента вязкости жидкости. Проверка закона СтоксаСкачать

Рассмотрим падение шарика в вязкой жидкости

При движении шарика слой жидкости, граничащий с его поверхностью, прилипает к шарику и движется со скоростью шарика. При вычислении сопротивления среды следует учитывать трение отдельных слоев жидкости друг о друга, а не трение шарика о жидкость.

На шарик, падающий в вязкой жидкости, действуют три силы (рис. 2.2):

· сила тяжести F₁= mg = p_ш×V×g;

· сила Архимеда F_А = p_ж×V×g (равная весу жидкости в объеме шарика);

· сила сопротивления, обусловленная вязкостью жидкости:

F = 6p×h×r×v,

где r_ш – плотность материала шарика;

r_ж – плотность жидкости;

V – объем шарика;

g – ускорение свободного падения.

Все три силы направлены по вертикали: F₁ – вниз, F₂ и F₃ – вверх.

В общем случае уравнение движения шарика имеет вид

Сила сопротивления с увеличением скорости движения шарика возрастает, а ускорение dv/dt уменьшается до тех пор, пока шарик не достигнет такой скорости, при которой ускорение равно 0.

Тогда уравнение (2.3) примет вид:

в этом случае шарик движется с постоянной скоростью v₀.

Решая (2.4) относительно h, получим

(2.5)

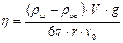
Если теперь учесть, что V = r 3 , r = d/2, v₀ = l/t,

где d – диаметр шарика;

l – длина участка равномерного движения, пройденного за время t,

то формула (2.5) примет окончательный вид

(2.6)

Таким образом, для нахождения h нужно измерить d, l и t.

Рассмотрим подъем шарика в вязкой жидкости.

Если два одинаковых шарика связаны невесомой нитью, перекинутой через блок, причем один из шариков будет погружен в сосуд с жидкостью (2.3.), то уравнения движения шарика имеют вид:

(2.7)

В уравнениях (2.7)

I – момент инерции диска;

R – радиус диска;

Т₁ и Т₂ – натяжение нитей,

F_тр – сила трения, обусловленная вязкостью жидкости,

F_А – сила Архимеда.

Сила сопротивления с увеличением скорости движения шарика возрастает, а ускорение уменьшается до тех пор, пока шарик не достигнет такой скорости v₀, при которой ускорение равно 0.

Тогда уравнения (2.7), при , принимают вид:

В этом случае шарик двигается с постоянной скоростью. Из (2.8) следует

(2.9)

или аналогично формуле (2.6) расчетная формула принимает вид:

(2.10)

В формуле (2.10) так же как и в формуле (2.6) нужно измерить d, l, t.

Описание установки.

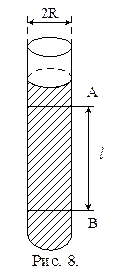
Длинный стеклянный цилиндр, наполненный исследуемой жидкостью, имеет две горизонтальные метки А и В, расположенные на расстоянии l друг от друга. Метка А установлена так, что при прохождении через нее шарик уже имеет постоянную скорость v₀ (см. рис 2.2).

При измерении вязкости при подъеме шарика применяется схема (рис. 2.3): на краю стеклянного цилиндра установлен блок, через который перекинуты шарики, связанные нитью. Для определения вязкости при подъеме шарика, один шарик опускают на дно цилиндра с жидкостью.

Видео:Движение тел в жидкостях и газах. Лобовое сопротивление и подъемная сила. Формула Стокса. 10 класс.Скачать

Ламинарное движение шарика в жидкости. Формула Стокса

Стоксом было получено строгое решение задачи о ламинарном обтекания шарика безграничной жидкостью. В этом случае сила сопротивления F определяется формулой

, (14)

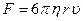
где h – коэффициент внутреннего трения жидкости, u –скорость шарика, r – радиус шарика.

Гидродинамический вывод формулы Стокса довольно сложен. Поэтому ограничимся анализом задачи с помощью теории размерности. На основании физических соображений и опыта можно считать, что сила F должна определяться параметрами h, u, r и плотностью жидкости r_ж. Искомый закон следует искать в виде степенного соотношения

, (15)

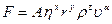
где А – безразмерный множитель, а x, y, z и a – подлежащие определению показатели степени. Выбор показателей степени определяется из того условия, что размерности левой и правой частей должны совпадать. Из опыта известно, сто при малых скоростях движения тела (ламинарное течение) сила сопротивления пропорциональна скорости (показатель степени a=1). Приравнивая показатели степени по массе, длине и времени в левой и правой частях уравнения (15), получим

1 = x + z, 1 = -x + 1 + y — 3z, -2 = -x — 1; (16)

x = 1, y = 1, z = 0. (17)

Таким образом получим

Безразмерный множитель А не может быть определен из соображения размерности, но строгое решение этой задачи дает для этого множителя значение 6p.

Рассмотрим свободное падение шарика в вязкой жидкости. На шарик действуют сила тяжести, архимедова сила и сила вязкого трения, зависящая от скорости u. На основании второго закона механики будем иметь

, (19)

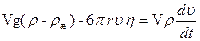
где V – объем шарика, r – его плотность, r_ж – плотность исследуемой жидкости, g – ускорение силы тяжести.

Решая это уравнение найдем

, (20)

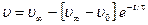
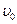
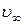
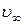
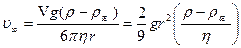
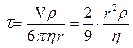
где – скорость шарика в момент начала его движения, которая в опытах обычно равна нулю, – установившаяся скорость движения шарика, t – время релаксации. При этом величины и t соответственно равны

; . (21)

Из уравнения (20) видно, что скорость шарика экспоненциально приближается к установившейся скорости 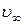. Установление скорости определяется временем релаксации t. Если время падения шарика в несколько раз больше времени релаксации (t>>t), то процесс установления скорости можно считать закончившимся.

Поэтому для некоторой части пути, ограниченной метками А и В, где движение шарика будет равномерным, скорость шарика равна

где l – расстояние, t – время падения шарика между метками А и В.

Подставляя значение скорости в уравнение (21), получим:

. (23)

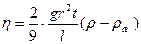
Данное уравнение справедливо лишь тогда, когда шарик падает в безграничной среде. Если шарик падает вдоль оси трубки радиуса R, то приходится учитывать влияние стенок, т.е. ввести поправки на влияние боковых стенок. Формула для определения коэффициента вязкости с учетом поправок принимает следующий окончательный вид:

. (24)

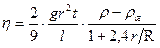
Соотношение (24) используется для определения вязкости жидкостей методом Стокса. Опуская шарик радиусом r в сосуд с исследуемой жидкостью, и измеряя время t прохождения шариком некоторого расстояния l можно найти коэффициент внутреннего трения жидкости h.

При выводе формулы Стокса предполагалось, что обтекание шарика жидкостью имеет ламинарный характер. Известно, что характер обтекания определяется значением числа Рейнольдса, которое определяется из формулы (6)

. (25)

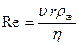
Для тел сферической формы обтекание будет ламинарным при условии Re

Дата добавления: 2015-12-16 ; просмотров: 5425 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Шарик массой 400 г всплывает с постоянной скоростью в жидкости, плотность которой в 3 раза большеСкачать

Движение тел в вязкой среде. Закон Стокса.

Вязкость проявляется не только при движении жидкости или газ; по сосудам, но и при движении тел в жидкости или газе. При небольшие скоростях тел, в соответствии с уравнением Ньютона, сила сопротивления движущемуся телу пропорциональна вязкости жидкости, скорости движения тела и зависит от размеров тела. Так как невозможно указать общую формулу для силы сопротивления, то ограничимся рассмотрением частного случая.

Наиболее простой формой тела является шар. Для него зависимость силы сопротивления от перечисленных выше факторов выражается законом Стокса:

F_c = 6π η r υ (8.23)

где r — радиус шара; υ — скорость его движения. Этот закон получен в предположении, что стенки сосуда не влияют на движение тела. Закон Стокса справедлив лишь при малых числах Рейнольдса (см. § 8.6).

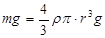
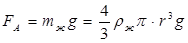
При падении шара в вязкой среде (рис. 8.12) на него действуют три силы: а) сила тяжести Р= ; выталкивающая (архимедова) сила , где m — масса вытесненной шаром жидкости, ρ_ж — ее плотность; в) F_тр— сила

сопротивления, вычисляемая по формуле (8.21).

Пусть шар, свободно падая в воздухе, попадает в жидкость. Жидкость тормозит движение шара и его скорость уменьшается. Так как сила сопротивления прямо пропорциональна cкорости, то и она будет уменьшаться до тех пор, пока движение не станет равномерным. В этом случае (рис. 8.12)

(8.24)

в скалярной форме

при подстановке соответствующих выражений для сил

(8.25)

υ₀ — скорость равномерного движения (падения) шара. Из (8.25) получаем

(8.26)

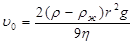
Отсюда запишем формулу, которую используют для нахождения вязкости:

(8.27)

§ 8.6 Ламинарное и турбулентное течения. Число Рейнольдса

Наблюдения показывают, что в жидкости возможны две формы движения: ламинарное движение и турбулентное.

Рассмотренное ранее течение жидкости является слоистым, или ламинарным.

Ламинарное течение — течение жидкости, при котором слои скользят друг относительно друга, не перемешиваясь (рис. а). Для него справедливы уравнения Бернулли и Пуазейля. Увеличение скорости течения вязкой жидкости (газа) вследствие неоднородности давления по поперечному сечению трубы создает завихрение, и движение становится вихревым или турбулентным.

Турбулентное течение — течение, сопровождающееся образованием вихрей и перемешиванием слоёв.

При турбулентном течении жидкости или газа скорость частиц в каждом месте непрерывно и хаотически изменяется, движение является нестационарным.

С увеличением скорости потока ламинарное течение может перейти в турбулентное, а скорость, при которой происходит этот переход, называется критической.

Характер течения жидкости в трубе зависит от свойств жидкости, скорости её течения, размеров трубы и определяется так называемым числом Рейнольдса:

(8.28)

ρ_ж — плотность жидкости (газа); υ— средняя по сечению трубыскорость жидкости (газа); d — диаметр трубы.

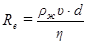
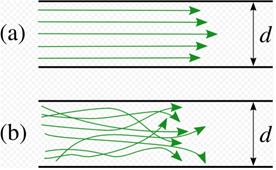
При малых значениях числа Рейнольдса наблюдается ламинарное течение; при (Rе > Rе_кр), (Rе_кр критическое значение) ламинарное течение переходит в турбулентное. Например, для гладких цилиндрических труб Rе_кр ≈ 2300.

Примеры решения задач

Пример . Полый шар плавает на границе двух несмешивающихся жидкостей (см. рисунок) так, что соотношение частей шара во второй и первой жидкости равно . Плотности жидкостей и тела соответственно равны ρ₁=0,8г/см 3 , ρ₂=1г/см 3 и ρ=2,7 г/см 3 . Определите объём шара V, если размер его внутренней полости V₀=20см 3 .

Дано: ; V₀=20см 3 =2∙10 -5 м 3 ; ρ₁=0,8г/см 3 =8∙10 2 кг/м 3 ; ρ₂=1 г/см 3 =1∙10 3 кг/м 3 ; ρ=2,7 г/см 3 =2,7∙10 3 кг/м 3 .

Решение. Поскольку шар находится в равновесии, сила тяжести Р, действующая на тело, уравновешивается силой Архимеда F_А:

(ρ – плотность материала шара; V- его объём; V₀— объём внутренней полости шара; g — ускорение свободного падения; m₁ и m₂ – соответственно масса жидкостей в объёмах V₁ и V₂), можно записать

Из выражения (1), учитывая, что V₂= n V₁ (условие задачи) найдём

Искомый объём шара

Пример . В сообщающиеся трубки с водой площадью сечения S=0,5см 2 долили в левую масло объёмом V₂=40мл, в правую керосин объёмом V₂=30мл. Определите разность Δh установившихся уровней воды в трубках, если плотность воды

ρ =1г/см 3 , плотность масла ρ₁=0,9 г/см 3 , плотность керосина ρ₂=0,8 г/см 3 .

Дано: S=0,5 см 2 =0,5∙10 -4 м 2 ; V₁=40мл=4∙10 -5 м 3 ; V₂=30мл=3∙10 -5 м 3 ; ρ=1г/см 3 = 1∙10 3 кг/м 3 ; ρ₁=0,9 г/см 3 = 0,9∙10 3 кг/м 3 ; ρ₂=0,8 г/см 3 = 0,8∙10 3 кг/м 3 .

Решение. Предположим, что уровень воды в левом сосуде понизится (см. рисунок). Для уровня поверхности воды в левом сосуде давление равно давлению столба масла

, (1)

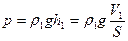
где h₁— высота столба масла; V₁— объём масла; S- площадь сечения трубки. Для правого сосуда давление на той же горизонтали будет равно сумме давлений столба керосина и избыточного столба воды высотой Δh

, (2)

где h₂— высота столба керосина.

Поскольку давление на одной горизонтали одинаково, приравняв выражения (1) и (2), найдём

Откуда искомая разность уровней

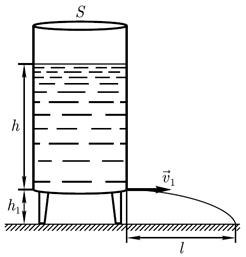
Пример 8.1.Открытый цилиндрический сосуд, стоящи на ножках высотой h₁=1,33м, заполнен водой до отметки h=3,8м (см. рисунок) . Пренебрегая вязкостью воды, определите площадь сечения S цилиндра, если через отверстие диаметром d₁=2.5 см у его основания струя, вытекающая из отверстия, падает на пол на расстоянии ℓ=4.5м от цилиндра.

Решение. Согласно уравнению неразрывности,

где υ – скорость понижения воды в баке; υ₁— скорость вытекания струи; S₁— площадь отверстия. Тогда

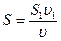
Согласно уравнению Бернулли для сечений S и S₁,

где р и р₁ – статические давления жидкости соответственно для поверхности воды и отверстия; — плотность воды. Учитывая, что р₁=р (бак открыт), из выражения (2) 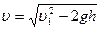. Подставив эту формулу в (1), найдём

(3)

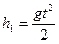
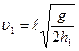
Согласно кинематическим уравнениям и ℓ=υ₁t (t — время падения струи воды на Землю), найдём

. (4)

Подставив (4) в (3) и учитывая, что 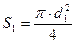, получаем искомую площадь сечения

Пример 8.1.Водомер представляет собой горизонтальную трубу переменного сечения, в которую впаяны две вертикальные манометрические трубки одинакового сечения. По трубе протекает вода. Пренебрегая вязкостью воды, определите её массовый расход, если разность уровней в манометрических трубках Δh=8 см, а сечения трубы у оснований манометрических трубок соответственно равны S₁= 6см 2 и S₂=12см 2 . Плотность воды ρ=1 г/см 3 .

Дано:Δh=8 см=0,08м; S₁= 6см 2 =6∙10 -4 м 2 ; S₂=12см 2 =12∙10 -4 м 2 ;

ρ=1 г/см 3 =1∙10 3 кг/м 3 .

Решение. Массовый расход воды- это масса воды, протекающая через сечение за единицу времени,

(1)

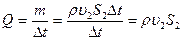
где ρ – плотность воды; υ₂— скорость течения воды в месте сечения S₂. При стационарном течении идеальной несжимаемой жидкости выполняется уравнение неразрывности

и уравнение Бернулли для горизонтальной трубы (h₁=h₂)

(3)

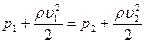
где р₁ и р₂ – статические давления в сечениях манометрических трубок; υ₁ и υ ₂ — скорость течения воды в местах сечений S₁ и S₂. Учитывая, что

и решая систему уравнений (2), (3), получаем

Подставив это выражение в (1), найдём искомый массовый расход воды:

Пример 8.1.Для определения объёма перекачки газа используется прибор, основанный на принципе действия трубки Пито (см. рисунок). При перекачке азота по трубе за время t =1мин проходит объём газа V=59,3м 3 . Определите диаметр трубы, если разность уровней воды в коленах трубки Пито Δh =1см. Плотность азота ρ =1,25 кг/м 3 , плотность воды ρ₁=1 г/см 3 .

Дано:t =1мин=60с; V=59,3м 3 ; Δh =1см =1∙10 -2 м; ρ =1,25 кг/м 3 ;

Решение. Согласно уравнению Бернулли, разность давлений газа, оказываемых на колена трубки (см.рисунок),

(1)

где ρ – плотность газа; υ- скорость течения газа.

С другой стороны, разность давлений в коленах определяется разностью уровней жидкости в коленах трубки

Приравняв выражения (1) и (2),

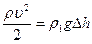
Найдём скорость движения тела

(3)

Объём газа V, перекачиваемого за время t

где S- площадь сечения трубы.

Подставляя в эту формулу выражение (3) и , найдём

Откуда искомый диаметр трубы

Пример 8.1.Пренебрегая вязкостью воды, определите объём V воды в цилиндрическом баке диаметром d=1м, если через отверстие диаметром d₁=2см на дне бака вся вода вытекла за время t=30мин..

Решение. Если за время dt уровень воды в баке понижается на dh, то уменьшение объёма воды за это же время

где S – площадь основания бака, а знак «-» указывает на то, что высота слоя воды уменьшается. С другой стороны уменьшение объёма воды за время dt

где S – площадь отверстия; υ — скорость истечения воды из отверстия, определяемая согласно формуле Торричелли (применима при S₁ 3 .

Пример 8.1.В области соприкосновения двух параллельно текущих слоёв воды их скорость изменяется, как показано на рисунке. Определите силу внутреннего трения F, если площадь S соприкосновения слоев равна 3м 2 . Динамическая вязкость воды η=10 -3 Па∙с.

Решение. Сила внутреннего трения между слоями текущей жидкости

, (1)

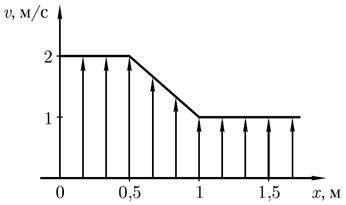
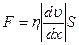
где η – динамическая вязкость жидкости; — градиент скорости; S — площадь соприкосновения слоёв.

Согласно заданному графику,

Подставляя значения физических величин в формулу (1), искомая сила внутреннего трения F=6∙10 -3 Н.

Пример 8.1.Шарик радиусом r=2мм падает в глицерине с постоянной скоростью υ=8,5 мм/с. Определите число Рейнольдса Re и плотность ρ₁ материала шарика, если критическое число Рейнольдса Re_кр =0,5.Плотность глицерина ρ=1,26г/см 3 , динамическая вязкость глицерина η=1,48 Па∙с.

Дано:r=2мм =2∙10 -3 м; υ=8,5мм/с=8,5∙10 -3 м/с; Re_кр =0,5; η=1,48 Па∙с; ρ=1,26г/см 3 =1,26∙10 3 кг/м 3 ).

Решение. Характер течения жидкости зависит от числа Рейнольдса, определяемого формулой

где ρ– плотность жидкости; υ — скорость жидкости; d — диаметр шарика; η — динамическая вязкость жидкости. Учитывая данные задачи, получаем Re=0,029. Поскольку Re 3 .