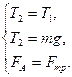Уравнение движения шарика в жидкости (7 видео)

Рассмотрим падение шарика в вязкой жидкости

При движении шарика слой жидкости, граничащий с его поверхностью, прилипает к шарику и движется со скоростью шарика. При вычислении сопротивления среды следует учитывать трение отдельных слоев жидкости друг о друга, а не трение шарика о жидкость.

На шарик, падающий в вязкой жидкости, действуют три силы (рис. 2.2):

· сила тяжести F₁= mg = p_ш×V×g;

· сила Архимеда F_А = p_ж×V×g (равная весу жидкости в объеме шарика);

· сила сопротивления, обусловленная вязкостью жидкости:

F = 6p×h×r×v,

где r_ш – плотность материала шарика;

r_ж – плотность жидкости;

V – объем шарика;

g – ускорение свободного падения.

Все три силы направлены по вертикали: F₁ – вниз, F₂ и F₃ – вверх.

В общем случае уравнение движения шарика имеет вид

Сила сопротивления с увеличением скорости движения шарика возрастает, а ускорение dv/dt уменьшается до тех пор, пока шарик не достигнет такой скорости, при которой ускорение равно 0.

Тогда уравнение (2.3) примет вид:

в этом случае шарик движется с постоянной скоростью v₀.

Решая (2.4) относительно h, получим

(2.5)

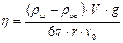
Если теперь учесть, что V = r 3 , r = d/2, v₀ = l/t,

где d – диаметр шарика;

l – длина участка равномерного движения, пройденного за время t,

то формула (2.5) примет окончательный вид

(2.6)

Таким образом, для нахождения h нужно измерить d, l и t.

Рассмотрим подъем шарика в вязкой жидкости.

Если два одинаковых шарика связаны невесомой нитью, перекинутой через блок, причем один из шариков будет погружен в сосуд с жидкостью (2.3.), то уравнения движения шарика имеют вид:

(2.7)

В уравнениях (2.7)

I – момент инерции диска;

R – радиус диска;

Т₁ и Т₂ – натяжение нитей,

F_тр – сила трения, обусловленная вязкостью жидкости,

F_А – сила Архимеда.

Сила сопротивления с увеличением скорости движения шарика возрастает, а ускорение уменьшается до тех пор, пока шарик не достигнет такой скорости v₀, при которой ускорение равно 0.

Тогда уравнения (2.7), при , принимают вид:

В этом случае шарик двигается с постоянной скоростью. Из (2.8) следует

(2.9)

или аналогично формуле (2.6) расчетная формула принимает вид:

(2.10)

В формуле (2.10) так же как и в формуле (2.6) нужно измерить d, l, t.

Описание установки.

Длинный стеклянный цилиндр, наполненный исследуемой жидкостью, имеет две горизонтальные метки А и В, расположенные на расстоянии l друг от друга. Метка А установлена так, что при прохождении через нее шарик уже имеет постоянную скорость v₀ (см. рис 2.2).

При измерении вязкости при подъеме шарика применяется схема (рис. 2.3): на краю стеклянного цилиндра установлен блок, через который перекинуты шарики, связанные нитью. Для определения вязкости при подъеме шарика, один шарик опускают на дно цилиндра с жидкостью.

Содержание

Лабораторные работы по электротехнике
Измеряем вязкость жидкости
Работа с прибором
🔍 Видео

Видео:Определение коэффициента вязкости жидкости методом СтоксаСкачать

Лабораторные работы по электротехнике

ОПРЕДЕЛЕНИЕ ВЯЗКОСТИ ЖИДКОСТИ

Приборы и принадлежности: сосуд с известной жидкостью, микрометр, секундомер, стальные шарики.

Цель работы: определить динамическую и кинематическую вязкости жидкости методом Стокса.

Если происходит движение одного слоя реальной жидкости относительно другого, то при различной относительной скорости движения этих слоев возникают силы внутреннего трения, которые зависят от степени вязкости жидкости. Внутреннее трение подчиняется закону Ньютона:

где f — сила внутреннего трения, действующая на единицу площади поверхностности слоя; h — динамическая вязкость; — градиент скорости по направлению внешней нормали п к поверхности слоя. Знак минус указывает, что сила трения направлена против скорости. Динамическая вязкость (коэффициент внутреннего трения) h равна численно силе внутреннего трения, действующей на единицу площади поверхности слоя при градиенте скорости, равном единице.

Силы сопротивления движению возникают и при падении тела внутри покоящейся жидкости. При этом вокруг движущегося тела возникает мономолекулярный слой жидкости, молекулы которого как бы прилипают к телу за счет сил сцепления и увлекаются этим телом, т.е. имеют скорость движения, равную скорости этого тела.

Этот мономолекулярный слой жидкости, движущейся со скоростью данного тела, увлекает за собой соседние слои жидкости, но с меньшими скоростями, причем чем дальше от тела отстоит слой жидкости, тем с меньшей скоростью он движется по сравнению со скоростью тела.

Силы внутреннего трения действуют со стороны удаленных частиц на прилегающие к телу частицы жидкости, тормозят их и, являясь силами сопротивления, направлены в сторону противоположную скорости тела.

Опытным путем было установлено, что сила сопротивления среды зависит от скорости движения тела, его линейных размеров, состояния поверхности тела и вязкости среды.

Силу сопротивления среды Fс можно наиболее просто определить для тела сферической формы, падающего в покоящейся жидкости. По Стоксу, сила сопротивления среды

где h – динамическая вязкость жидкости; d — диаметр шарика; u — скорость шарика.

Формула Стокса (13.1) положена в основу метода определения вязкости жидкости.

Рассмотрим динамику движения шарика в жидкости (рис.13.1). На шарик, движущийся в жидкости, кроме силы сопротивления Fс действуют еще две силы: сила тяжести Fт= mg= r шVg и выталкивающая сила (сила Архимеда): где r ш — плотность материала шарика; r ж — плотность жидкости; V — объем шарика; g — ускорение свободного падения.

По второму закону Ньютона (в проекциях на ось x) имеем

где а — ускорение шарика

Сила тяжести и сила Архимеда остаются неизменными в данном опыте, а сила сопротивления Fс увеличивается по мере возрастания скорости шарика. При этом ускорение шарика будет уменьшаться до тех пор, пока не станет равным нулю. Дальнейшее движение шарика происходит равномерно со скоростью v, которую приобретает шарик к Рис. 13.1 этому моменту.

Итак, при равномерном движении шарика a=0, и из (13.2) получаем

Подставив это значение силы сопротивления Fс в формулу Стокса (13.1), получим

Подставляя значение объема шарика V= p d3/6 и решая уравнение (13.3) относительно h , находим вязкость жидкости

Скорость u можно определить, используя уравнение равномерного движения

где s — расстояние, пройденное шариком равномерно; t — время его движения.

Окончательно для динамической вязкости имеем формулу

Следует иметь в виду, что коэффициент вязкости сильно зависит от температуры и с ее ростом уменьшается.

Кроме динамической вязкости часто используется понятие кинематической вязкости

где — плотность жидкости.

Установка для определения вязкости представляет собой стеклянный цилиндр, заполненный испытуемой жидкостью (например, глицерином, вазелиновым маслом) закрепленный в вертикальном положении (рис.13.2).

На цилиндре имеются подвижные кольца А и В, которыми фиксируется путь, пройденный шариком в равномерном движении. Верхнее кольцо А должно быть установлено не менее, чем на 20 см ниже уровня жидкости: на этом пути движения шарика стабилизируется. Кольцо В устанавливают как можно дальше от кольца А. Расстояние между кольцами измеряют и записывают. Время падения шарика измеряют электрическим секундомером, который прилагается к установке.

Следует учесть, что погрешность в определении времени падения шарика определяет погрешность результата измерений вязкости.

Порядок выполнения работы

. ПРЕДОСТЕРЕЖЕНИЕ . В стеклянный цилиндр нельзя кидать посторонние предметы. Доставать шарики со дна цилиндра разрешается только лаборанту.

1.Отберите для опыта пять шариков. Микрометром измерьте диаметр каждого шарика в трех различных направлениях и записывают в таблицу.

2.Установите кольца А и В, как описано выше, измерьте расстояние между ними.

3. Шарик бросьте в жидкость как можно ближе к оси сосуда и, наблюдая за его падением, фиксируйте время падения t шарика между кольцами А и В (реагируйте быстро, так как время падения мало!). Опыт повторите с каждым из пяти шариков. Данные опытов занесите в таблицу 13.1.

4. Запишите плотность шариков (сталь) r ш=7900 кг/м3 и плотность исследуемой жидкости (глицерин) r ж=1260 кг/м3. По результатам каждого опыта по формуле (13.4) вычислите динамическую вязкость жидкости, найдите среднее значение и сравните его с табличными данными.

Видео:Движение тел в жидкостях и газах. Лобовое сопротивление и подъемная сила. Формула Стокса. 10 класс.Скачать

Измеряем вязкость жидкости

Экспериментальная задача по измерению вязкости жидкости была сформулирована нашим учителем в виде отдельных терминов и фраз, которые для получения условия нужно было связать воедино. Выглядела она так: измерение вязкости электронный секундомер шарик тонет формула Стокса

Метод Стокса, с помощью которого должна решаться задача, является общеизвестным и широко применимым (к примеру, в медицине его используют для измерения вязкости плазмы крови). Необычность же предлагаемого способа заключается в применении компьютера с электронным блоком сопряжения для повышения точности и быстроты измерений.

На движущийся в жидкости шарик действует сила трения, тормозящая его движение. При условии, что диаметр шарика заметно меньше диаметра сосуда, эту силу можно вычислить по закону Стокса:

Где r-радиус шарика, v-его скорость. Если шарик свободно падает в вязкой жидкости, то на него, кроме силы трения, будут действовать направленная вниз сила тяжести и направленная вверх архимедова сила.

На основании второго закона Ньютона получаем запись: m dv/dt=ρVg — ρ1Vg — 6πηrv

В этом уравнении сила сопротивления имеет переменное значение. Поскольку с течением времени эта сила растет, то ускорение движения уменьшается до нуля и движение шарика становится равномерным. В этот момент сила тяжести, действующая на шарик, оказывается равной сумме сил трения и архимедовой силы.

Отсюда следует, что скорость равномерного движения шарика может быть определена уравнением: v=Vg(ρ – ρ1)/6πηr

Существенно то, что эта скорость пропорциональна разности плотностей шарика и жидкости. Поэтому, чем ближе плотность шарика к плотности жидкости, тем меньше скорость равномерного движения шарика и тем точнее она может быть измерена. Кроме этого необходимо, чтобы обтекание шарика жидкостью было ламинарным, что также достигается при малых скоростях движения. В вискозиметрах заводского изготовления с этой целью применяется набор различных шариков, чтобы можно было измерять вязкость в большом диапазоне значений.

Если учесть, что объем шара V=4πr3 /3, то полученное уравнение изменяется:

Таким образом, для определения вязкости жидкости нужно измерить ее плотность, плотность материала шарика, его радиус и скорость движения.

Измерение скорости равномерного движения с достаточно большой точностью и является главной проблемой в этом опыте. С этой целью в нашей школе мы применяем инфракрасные датчики положения и электронный блок сопряжения с компьютером.

Видео:Определение коэффициента вязкости жидкости. Проверка закона СтоксаСкачать

Работа с прибором

Для проведения опыта потребуется стеклянная трубка такого сечения, чтобы она входила в корпус инфракрасных датчиков положения, шарик с диаметром заметно меньшим, чем диаметр трубки, весы, измерительный цилиндр и штангенциркуль.

Если диаметр шарика соизмерим с диаметром трубки, то в найденное значение вязкости придется вводить поправочный коэффициент h/(R + 0. 24r)(h + 1. 33r), где h – высота жидкости в трубке, R – радиус трубки, r — радиус шарика.

С помощью весов и штангенциркуля находим массу и объем шарика, чтобы вычислить его плотность. Для определения плотности жидкости применим измерительный цилиндр и весы.

С помощью штатива закрепляем трубку в вертикальном положении и заполняем ее исследуемой жидкостью. В нижней части трубки устанавливаем инфракрасные датчики на любом известном расстоянии друг от друга. Роняем шарик в жидкость, чтобы убедиться в том, что в процессе падения он не задевает стенок трубки и перекрывает инфракрасный луч, включая секундомер. Для удобства проведения опыта желательно использовать несколько одинаковых шариков, чтобы не добывать его каждый раз из жидкости.

После всех этих подготовительных действий можно ввести в компьютер программу, обслуживающую секундомер и произвести измерение скорости движения шарика. Значение скорости появится на экране монитора после введения с клавиатуры значения расстояния между датчиками, соответствующий вопрос появится в диалоговом окне сразу, как только шарик пройдет мимо инфракрасных датчиков положения. Поскольку прибор является многофункциональным, то он выдаст на экран значения времени движения, максимальной скорости, дальности и т. д. На эти числа внимания не обращаем, а используем для работы только величину средней скорости.

Скорость движения шарика в воде 0,0016 м/с

Масса шарика 0,55 г

Диаметр шарика 10 мм

Внутренний диаметр трубки 12,5 мм

Расстояние между датчиками 0,5 м

Температура в помещении 19 градусов

Произведенные измерения дают такой результат для вязкости воды:

η = 0,0010334 Па * с, что хорошо согласуется с табличным значением при данной температуре.