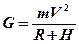Уравнение движения самолета в перегрузках (2 видео)

ПЕРЕГРУЗКИ В КРИВОЛИНЕЙНОМ ПОЛЕТЕ

3.3.1. Общие выражения для определения перегрузок
при движении самолета в вертикальной плоскости

Перегрузки при движении самолета в вертикальной плоскости определим из соответствующих уравнений движения самолета. Эти уравнения в поточной системе координат (см. рис. 3.1) могут быть записаны так:

где 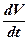и — тангенциальное и нормальное ускорения соответ-ственно, м/с 2 ;

r — радиус кривизны траектории, м;

Ө— местный угол наклона траектории, градусы;

V — скорость полета, м/с;

— центростремительное ускорение, обусловленное кривизной поверхности Земли;

Ry 6 370 000 м — радиус Земли;

Н — высота полета, м.

Центробежные силы инерции , обусловленные кривизной поверх-ности Земли, надо включать в уравнения (3.5) лишь при больших скоростях полета (М > 6 …7).

Разделив левые и правые части уравнений (3.5) на силу тяжести G, получим формулы для определения тангенциальной и нормальной перегрузок, выраженных через поверхностные силы:

Аналогично через массовые силы:

Здесь — первая космическая скорость, которая равна 7,92 км/с ;

g — ускорение силы тяжести.

При числе Маха М ‘

Определяя знаки перед членами выражения (3.7в), можно пользоваться следующими правилами:

Рис. 3.3 Определение знаков перед членами выражения (3.7в)

1. Если вектор силы тяжести самолета проектируется на отрицательное направление оси у (рис. 3.3), то перед cosθ ставят знак «плюс», в противном случае — «минус».

2. Второй член принимают сплюсом, если положительное направление оси у обращено в сторону вогнутости траектории, в противном случае перед ним надо ставить знак «минус».

3.3.2. Горизонтальный полет.

Вустановившемся горизонтальном полете , sinθ = 0, cosθ = 1 и из выражения (3.7) получим

Условие п_у = 1 обязательно для горизонтального полета. Продольная перегрузки п_х, может отличаться от нуля, но при этом полет протекает с ускорением.

3.3.3. Перегрузки при криволинейном полете в горизонтальной
плоскости.

В случае обычной схемы самолета криволинейный полет в горизонтальной плоскости (вираж) выполняется с креном (рис. 3.4).

сила y·sing искривляет траекторию. Здесь
g — угол крена.

Если скольжение на крыло отсутствует, то боковая перегрузка n_z = 0. Поперечная перегрузка определяется из условия равновесия самолета

Y· cos у = G:

Рис. 3.4 Нагрузки при вираже

С увеличением угла крена перегрузка п_у возрастает. При g = 70° величина п_ублизка к 3.

В полете со скольжением и при изменении высоты перегрузка может существенно отличаться от значения, получаемого по формуле (3.8).

Перегрузки п_у, которые обычно достигаются при маневрах

Маневр	п_у
Вираж	3…5
Боевой разворот	3…6
Бочка	4…5
Петля Нестерова	5…6
Спираль	3…5
Полупетля с переворотом	4…5
Бочка многократная	5…7

3.3.4. Полет вне границ атмосферы.

В этом случае аэродинамические силы y = 0, Q = 0 (рис. 3.5) и согласно выражению (3.6) перегрузки в направлении связанных осей координат равны

Если двигатель не работает (Р = 0), то
п_х = п_у = 0.

Из уравнения (3.5 б) следует, что при движении аппарата по круговой орбите с неработающим двигателем (Р = 0, Y= 0, cosθ = 1, 𝜃’ = 0) вес его уравновешивается центробежными силами инерции, обусловленными кривизной поверхности Земли:

Это условие выполняется при скорости полета, равной первой космической
скорости V = V_k₁

3.4. Перегрузки масс, не лежащих в центре тяжести
самолета

Если вращение самолета относительно центра тяжести отсутствует и он рассматривается как жесткое тело, то все его части испытывают одинаковые ускорения и одинаковые перегрузки, равные перегрузкам п_Уои п_хов центре тяжести.

При вращении самолета с угловой скоростью ω и ускорением e линейные ускорения в различных его точках будут неодинаковыми. В i – ой точке самолета (рис. 3.6), расположенной на расстоянии хот центра тяжести (ц. т.), добавятся ускорения относительного движения — нормальное Dj_n= — ω 2 x и тангенциальное Dj_τ = ex.

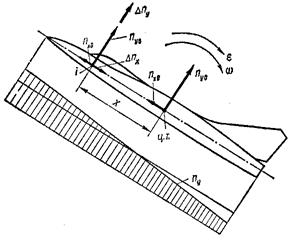
Этим ускорениям соответствуют перегрузки

Суммарные перегрузки i-ой массы при этом равны

(3.9)

В общем случае составляющие перегрузки i-ой массы, расположенной на оси самолета на удалении хот центра тяжести равно

; ;

где 𝛚_y, 𝛚_z — угловые скорости относительно осей у иzсоответственно.

Их размерность с -1 ;

— угловые ускорения относительно тех же осей, с -2 ;

М_у, М_г, J_y, J_z — моменты поверхностных сил и массовые моменты инерции самолета относительно осей у и z соответственно. По длине самолета перегрузки изменяются линейно (см. рис. 3.6).

Пример.Приняв 𝝎_z = 0,25 с -1 и расстояние массы от центра тяжести самолета равным х = 5 м, найдем дополнительную перегрузку Dп_х в точке i:

Дополнительная перегрузка Dп_у обычно больше.

Например, полагая маневренную нагрузку на оперении p_ман = 3000 кгс, плечо горизонтального оперения L_го= 5 м, момент инерции самолета
J_z = 5000 кгс×с 2 ×м, найдем, что

Видео:Тренировка в центрифуге. Перегрузка в 7,6 G на лётчика.Скачать

Уравнения движения центра масс самолета

Самолет движется в воздухе по действием аэродинамической силы 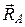, силы тяги двигателей и силы тяжести . С аэродинамической силой и ее проекциями на оси различных систем координат мы познакомились при изучении основ аэродинамики. Сила тяги создается силовой установкой самолета. Вектор обычно располагается в базовой плоскости самолета и образует некоторый угол с осью 0X связанной системы координат, но для простоты мы будем полагать, что этот угол равен нулю, а сам вектор приложен в центре масс.

Полет самолета можно условно разбить на несколько этапов: взлет, набор высоты, горизонтальный полет, снижение и посадка. Самолет также может совершать вираж и другие маневры. На некоторых этапах полета движение самолета может быть как установившимся, так и неустановившимся. При установившемся движении самолет летит с постоянной скоростью, при неизменных углах атаки, крена и скольжения. Ниже мы будем рассматривать только установившееся движение на этапах горизонтального полета, набора высоты и снижения.

Установившийся горизонтальный полет – это прямолинейный полет с постоянной скоростью на постоянной высоте (см. рис. 39). Уравнения движения центра масс самолета запишутся в этом случае следующим образом:

(48)

Поскольку угол атаки a мал (при этом cos a » 1, а sin a » 0), то можно записать:

(49)

Рис. 39. Схема сил, действующих на самолет в установившемся

Если первое из этих равенств не будет выполняться, то скорость самолета будет либо увеличиваться, либо уменьшаться, т.е. не будет выполняться условие установившегося движения. Если же подъемная сила не равна силе тяжести, то самолет будет либо подниматься, либо снижаться, а это значит, что не будет выполняться условие горизонтального полета. Из этого равенства, зная формулу подъемной силы (35), можно получить величину скорости, необходимую для выполнения горизонтального полета V_г.п.

Учитывая, что G = mg (где m – масса самолета, а g – ускорение свободного падения), можно записать:

, (50)

(51)

Из этой формулы видно, что скорость горизонтального полета зависит от массы самолета, плотности воздуха r (которая зависит от высоты полета), площади крыла S_кр и коэффициента подъемной силы C_ya. Поскольку C_ya напрямую зависит от угла атаки a, то каждому значению скорости горизонтального полета будет соответствовать единственное значение угла атаки. Поэтому для обеспечения установившегося горизонтального полета с требуемой скоростью летчик задает определенную тягу двигателей и величину угла атаки.

Установившийся набор высоты – прямолинейное движение самолета вверх с постоянной скоростью. Схема сил, действующих на самолет при установившемся наборе высоты с углом наклона траектории q, показана на рис. 40.

Рис. 40. Схема сил, действующих на самолет при установившемся

наборе высоты (угол атаки принят малым и не показан)

В этом случае уравнения движения примут вид:

(52)

Необходимо отметить, что при наборе высоты тяга двигателей P уравновешивает не только силу лобового сопротивления X_a, как в горизонтальном полете, но и составляющую силы тяжести Gsinq. Подъемная сила Y_a при этом требуется меньшая, поскольку Gcosq

Видео:Основы динамики самолета, крен, тангаж и рысканье - Основы Авиации #3Скачать

ОБЩИЕ СВЕДЕНИЯ ПО ДИНАМИКЕ ПОЛЕТА ВС

Динамика полета — это наука о законах движения летательных аппаратов (в данном случае — самолета). Основная задача динамики полета- выявление закона движения самолета под действием заданных сил и моментов (или определение системы сил и моментов, необходимой для реализации заданного закона движения). Другой весьма важной задачей динамики полета является определение закона движения самолета, обеспечивающего экстремальное (максимальное или минимальное) значение какого-либо параметра (максимальной дальности полета, минимального времени выхода заданную точку и т. п.). При изучении Курс основ динамики полета обычно делят на два раздела. В первом разделе изучают законы движения центра тяжести самолета, т. е. законы движения самолета как материальной точки. В этом случае силы, действующие на самолет, приложены в центре тяжести его, а моменты внешних сил уравновешены. Во втором разделе рассматривают движение самолета как твердого тела. При этом изучают общий случай движения тела с учетом, как перемещения центра тяжести, так и вращения относительно его под действием моментов внешних сил. В этом разделе исследуют моменты, приложенные к самолету, и характер движения его. Основные положения динамики полета самолета как науки были разработаны в работах Н. Е. Жуковского по аэродинамике и авиации. В работе «О парении птиц»(1891 г.) он анализирует условия выполнения полета и различные траектории движения при различных положениях центра тяжести. Среди рассмотренных траекторий была траектория вида «мертвой петли». Практические выводы, сделанные Н. Е. Жуковским, подтвердил П. Н. Нестеров, впервые в мире совершивший петлю в вертикальной плоскости («петля Нестерова»). В разработке методов расчета неустановившихся движений самолета большое значение имели работы одного из учеников Н. Е. Жуковского В. П. Ветчинкина «Динамика полета самолета» (1933 г.), а также В. С. Пышнова, А. Н. Журавченко, Б. Т. Горощенко и других советских ученых. Решению проблем динамики переменной массы посвящены труды К. Э. Циолковского и И. В. Мещерского.

СИЛЫ, ДЕЙСТВУЮЩИЕ НА САМОЛЕТ В ПОЛЕТЕ.ВИДЫ ДВИЖЕНИЯ САМОЛЕТА

Величина и направление скорости движения самолета зависят от величины и направления внешних сил, действующих на него. Эти силы являются результатом воздействия на самолет воздушной среды, массы воздуха, отбрасываемой двигателем, и массы Земли. В результате взаимодействия самолета с воздушной средой появляются аэродинамические силы. Воздух, отбрасываемый двигателем, вызывает появление силы тяги. Сила веса самолета есть результат действия на него массы Земли.

Таким образом, на летящий самолет действуют силы веса G, аэродинамическая R и тяги Р двигателя (см. рисунок ниже). Сила веса G приложена в центре тяжести самолета и направлена по радиусу к центру тяжести Земли. Аэродинамическая сила R приложена в центре давления. В общем случае она может быть заменена тремя составляющими: подъемной силой Y, силой лобового сопротивления К и боковой силой Z. Сила Y направлена перпендикулярно к вектору скорости, сила X — по касательной к траектории движения, а боковая сила Z — по нормали к плоскости сил Y и X. Силы Y и X лежат в плоскости симметрии самолета.

Сила тяги двигателя Р, как правило, действует в плоскости симметрии самолета. Она может иметь две составляющие: Рх — проекция на касательную к траектории движения и Ру — проекция на нормаль к траектории (см.рисунок ниже).

Ввиду малого значения составляющей Ру принимают, что сила тяги Р направлена по касательной к траектории движения самолета.

В первом разделе динамики полета принимают моменты всех сил относительно центра тяжести самолета уравновешенными. Поэтому все внешние силы можно приложить в центре тяжести самолета. В дальнейшем будут рассмотрены различные виды движений самолета под действием внешних сил R, Р и G, приложенных в его центре тяжести. Все силы, направленные параллельно вектору скорости, называются продольными, а перпендикулярно к вектору скорости — поперечными. Сила веса G может быть или продольной (отвесное пикирование), или поперечной (горизонтальный полет),или иметь продольные и поперечные составляющие (планирование, подъем самолета). Сила тяги может тоже иметь как продольную, так и поперечную составляющую (Рх и Ру).В каждый момент самолет при движении имеет вполне определенные величину и направление скорости. Если направление скорости со временем не изменяется, то полет самолета будет прямолинейным, в противном случае — криволинейным. Если при этом сохраняется величина скорости, то движение самолета будет равномерным. При увеличении скорости движение самолета будет ускоренным, при уменьшении — замедленным. Движение самолета с положительным ускорением называется разгоном, а с отрицательным ускорением — торможением. Следует заметить, что величина и направление скорости еще не дают полной характеристики полета. Поэтому чаще полет самолета характеризуется понятием «режим полета». Под режимом полета самолета понимают не только величину и направление скорости, но и высоту полета, характер траектории, ускорение и другие параметры движения. Ранее указывалось, что вид движения самолета определяется величиной и направлением равнодействующих продольных и поперечных сил. Если равнодействующая продольных сил направлена вперед, то движение самолета ускоренное. Сама сила является ускоряющей. Если эта сила направлена назад, то движение самолета будет замедленным (торможение) Таким образом, продольные силы влияют на изменение величины скорости движения самолета

Так как равнодействующая поперечных сил R направлена вдоль радиуса кривизны траектории, то она является центростремительной силой. Эта сила искривляет траекторию движения в сторону своего действия. Векторы скорости V и поперечной силы Rп могут лежать в одной плоскости (плоскость криволинейного

движения) и в разных плоскостях. В последнем случае траектория движения будет пространственной (спираль, боевой разворот и другие виды движения).

УРАВНЕНИЯ ДВИЖЕНИЯ ЦЕНТРА ТЯЖЕСТИ САМОЛЕТА

Из механики известно, что движение свободного тела в пространстве можно представить состоящим из поступательного движения его центра тяжести и вращения тела относительно центра тяжести. В первом разделе динамики самолета рассматривается только движение центра тяжести. Поэтому уравнения, связывающие внешние силы с ускорениями, которые они сообщают самолету, составляются только для движения его центра тяжести (центра масс). Эти уравнения назвали уравнениями движения центра тяжести самолета. Они используются для определения количественных характеристик полета самолета и их качественного анализа.

Любое движение центра тяжести самолета можно разложить на движения его по трем взаимно перпендикулярным осям. Так как движение самолета рассматривается относительно воздушной среды, то уравнения движения центра тяжести изучаются относительно так называемой поточной или скоростной системы координат. За начало координат в этой системе принимают центр тяжести самолета (точка О). Ось Ох направляют по вектору скорости (по касательной к траектории движения). Ось Оу располагают в вертикальной плоскости перпендикулярно к вектору скорости, а ось Oz — перпендикулярно к плоскости хОу. Положительное направление осей показано на рисунке.

Система координат подвижная, перемещается вместе с самолетом, однако система не позволяет построить траекторию движения, а отражает лишь связь ускорения с внешними силами. При рассмотрении вопросов, связанных с вращением самолета относительно его центра тяжести, удобнее пользоваться так называемой связанной системой координат. Эта система позволяет любое вращательное движение заменить вращением относительно трех взаимно перпендикулярных осей, проходящих через центр тяжести (см. рисунок):

— продольная ось самолета Ох, расположенная в плоскости симметрии самолета параллельно корневой (центральной) хорде крыла;

— путевая, или вертикальная, ось самолета Оу, расположенная в плоскости симметрии самолета и перпендикулярная к продольной оси;

— поперечная ось самолета Oz, перпендикулярная к плоскости хОу.

Моменты внешних сил относительно оси Ох называются поперечными Мх, относительно оси Оz – путевыми Му и относительно оси Oz — продольными Mz.

Угол γ у поворота самолета относительно оси Ох называется углом крена. Угол β поворота самолета относительно оси Оу называется углом рыскания. И, наконец, угол поворота самолета относительно оси Oz называется углом атаки. Положительное направление вращения определяется по правилу «буравчика», ввинчиваемого по положительному направлению той или иной оси (по направлению движения часовой стрелки). Связанная система координат используется при изучении вопросов балансировки, устойчивости и управляемости самолета. Выразим уравнения движения центра тяжести самолета в скоростной (поточной) системе координат. Обозначим проекции равнодействующей внешних сил на оси координат соответственно через Fx, Fy и, проекции ускорений — через j_i, j_y и j_z и массу самолета через m_{с-та .} Тогда второе уравнение механики F= m_с-та j проекциях на оси координат выразится в следующем виде:

Ускорение , направленное по касательной к траектории движения, называют тангенциальным или продольным. Оно характеризует только изменение величины скорости. При > 0 происходит разгон самолета, при Х), или замедленным (Р 2 ,

r — радиус кривизны траектории, м.

Предыдущее равенство можно преобразовать в следующее:

Из этой формулы следует, что при больших скоростях в горизонтальном полете подъемная сила меньше веса самолета. При скорости V = подъемная сила горизонтального полета равна нулю. Эта скорость получила название первой космической скорости. Самолет в данном случае будет двигаться по траектории искусственного спутника Земли. Первая космическая скорость для земных условий составляет 7900 м/сек. Если полет самолета происходит с небольшими скоростями, подъемная сила мало отличается от веса самолета. Так, например, при скорости полета V = 2500 км/час подъемная сила меньше веса самолета всего на 1%. Это позволяет при анализе горизонтального полета современных самолетов считать, что Y=G.

Потребная скорость горизонтального полета

При горизонтальном полете на данном угле атаки должно быть выполнено равенство Y=G. Известно, что каждому углу атаки соответствует вполне определенное значение c_y. Для обеспечения равенства Y = G данному углу атаки должна соответствовать и вполне определенная величина скорости на заданной высоте полета. Скорость полета, необходимая для создания подъемной силы, равной весу самолета на данном угле атаки, называется п о т р е б н о й с к о р о с т ь ю г о р и з о н т а л ь н о г о п о л е т а.

Потребная скорость горизонтального полета зависит от угла атаки полета, т. е. с_у, от высоты полета, т. е. , и от удельной нагрузки на крыло . С ростом углов атаки до α = α_кр увеличивается коэффициент с_у. Потребная скорость горизонтального полета при этом уменьшается. На критическом угле атаки, при котором c_у = c_у_max потребная скорость горизонтального полета достигает минимального значения. Эта скорость получила название м и н и м а л ь н о т е о р е т и ч е с к о й .

Практически полет на критических углах атаки не производится. При полете на α = α_кр из-за сильного срыва воздушного потока с крыла, возможно сваливание самолета на крыло или на нос. Приближение к критическому углу атаки обнаруживается в полете по тряске самолета. После начала тряски угол атаки увеличивать опасно.

С целью обеспечения безопасности полета наибольшая допустимая величина с_у должна быть меньше c_у_max. Скорость полета, когда коэффициент подъемной силы c_у равен коэффициенту подъемной силы при тряске c_у _доп называется м и н и м а л ь н о д о п у с т и м о й.

За минимально допустимую скорость иногда принимают так называемую с к о р о с т ь с в а л и в а н и я или с р ы в а . Скорость, при которой происходит непроизвольное сваливание самолета на крыло или на нос, называется скоростью сваливания или скоростью срыва.

Так же, чем больше удельная нагрузка на крыло, тем больше потребная скорость горизонтального полета. У современных самолетов несущие способности крыльев малые, а удельные нагрузки на крыло повышенные (500-600 кГ/м 2 ). Поэтому потребные минимальные скорости горизонтального полета их имеют большое значение (200-300 км/час). С подъемом на высоту из-за

уменьшения массовой плотности воздуха ρ потребная скорость горизонтального полета увеличивается.

Потребная тяга горизонтального полета

Из условия постоянства скорости в горизонтальном полете следует, что должно быть равенство силы тяги Р и силы лобового сопротивления X.

Тяга, необходимая для уравновешивания лобового сопротивления самолета при полете на данной скорости (угле атаки), называется п о т р е б н о й т я г о й г о р и з о н т а л ь н о г о п о л е т а Р_г.п_..

Выясним факторы, влияющие на потребную тягу горизонтального полета. Каждому углу атаки полета соответствует вполне определенное аэродинамическое качество самолета.

Максимальное качество самолета соответствует наивыгоднейшему углу атаки. На этом угле атаки потребная тяга минимальна. На меньших и больших углах атаки потребная тяга будет больше. Так как каждому углу атаки соответствует определенная скорость (число М), то потребная тяга зависит от скорости (числа М) полета.

Разберем характер зависимости потребной тяги горизонтального полета от скорости для определенного веса самолета и высоты полета. С ростом скорости полета угол атаки становится меньше. Качество самолета до α = α_наив увеличивается, а на больших углах атаки уменьшается. Поэтому потребная тяга с ростом скорости, до скорости, соответствующей α = α_наив уменьшается, а при больших скоростях увеличивается. На рисунке представлен график, показывающий зависимость потребной тяги горизонтального полета от скорости, который назвали кривой Жуковского. Потребная тяга горизонтального полета зависит также от веса самолета и высоты полета. При полете на данном угле атаки с ростом веса самолета потребная тяга увеличивается.

Физически это означает, что для горизонтального полета более тяжелого самолета требуется большая подъемная сила. Это достигается увеличением потребной скорости. При увеличении последней растет сила лобового сопротивления X и как результат потребная тяга горизонтального полета. Это приводит к смещению всех точек кривой потребной тяги в сторону больших скоростей и тяг.

С увеличением высоты при постоянном угле атаки потребная скорость горизонтального полета увеличивается, а потребная тяга остается постоянной.

С подъемом на высоту вследствие уменьшения скорости звука увеличивается число М. Оно может оказаться больше М_кр. При полетах на М > М_кр возникает волновой кризис, появляется волновое сопротивление. Аэродинамическое качество самолета при том же су будет уменьшаться. Это приводит к интенсивному росту потребной тяги на V > V_кр.

ВЗЛЕТ И ПОСАДКА

Динамика полета как раздел аэромеханики рассматривает вопросы, связанные с реализацией различных траекторий полета самолета, которые определяются техническим заданием на проектирование. Для самолетов различного назначения различна и так называемая номенклатура режимов полета, однако для всех самолетов общими являются режимы взлета и посадки.

Взлет — это ускоренное движение самолета с момента страгивания на линии старта до момента одновременного достижения регламентируемых в техническом задании высоты и безопасной скорости взлета, обеспечивающих безопасность полета на участке начального набора высоты.

В конце разбега самолет достигает скорости отрыва, при которой можно безопасно оторвать самолет от земли и продолжать взлет. На высоте Н = 400 м уже должны быть убраны шасси, взлетно-посадочная механизация, двигатели переведены на режим крейсерского полета и самолет начинает полет по маршруту.

Взлет самолета состоит из следующих этапов: разбега, отрыва и разгона с подъемом.

Разбегом самолета называется ускоренное движение его по земле (воде), необходимое для набора скорости, при которой происходит безопасный отрыв. Разбег является равноускоренным движением самолета.