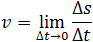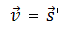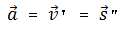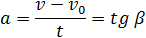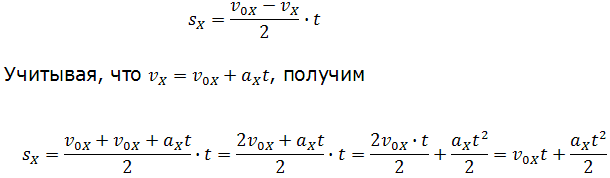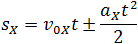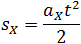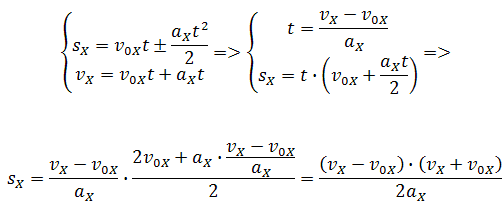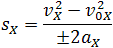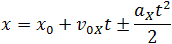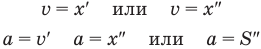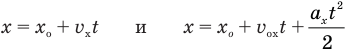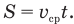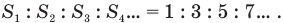Равномерное прямолинейное движение – это частный случай неравномерного движения.
Неравномерное движение – это движение, при котором тело (материальная точка) за равные промежутки времени совершает неодинаковые перемещения. Например, городской автобус движется неравномерно, так как его движение состоит в основном из разгонов и торможений.
Равнопеременное движение – это движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково.
Ускорение тела при равнопеременном движении остаётся постоянным по модулю и по направлению (a = const).
Равнопеременное движение может быть равноускоренным или равнозамедленным.
Равноускоренное движение – это движение тела (материальной точки) с положительным ускорением, то есть при таком движении тело разгоняется с неизменным ускорением. В случае равноускоренного движения модуль скорости тела с течением времени возрастает, направление ускорения совпадает с направлением скорости движения.
Равнозамедленное движение – это движение тела (материальной точки) с отрицательным ускорением, то есть при таком движении тело равномерно замедляется. При равнозамедленном движении векторы скорости и ускорения противоположны, а модуль скорости с течением времени уменьшается.
В механике любое прямолинейное движение является ускоренным, поэтому замедленное движение отличается от ускоренного лишь знаком проекции вектора ускорения на выбранную ось системы координат.
Средняя скорость переменного движения определяется путём деления перемещения тела на время, в течение которого это перемещение было совершено. Единица измерения средней скорости – м/с.
Мгновенная скорость – это скорость тела (материальной точки) в данный момент времени или в данной точке траектории, то есть предел, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Δt:
Вектор мгновенной скорости равнопеременного движения можно найти как первую производную от вектора перемещения по времени:
Проекция вектора скорости на ось ОХ:
это производная от координаты по времени (аналогично получают проекции вектора скорости на другие координатные оси).
Ускорение – это величина, которая определяет быстроту изменения скорости тела, то есть предел, к которому стремится изменение скорости при бесконечном уменьшении промежутка времени Δt:
Вектор ускорения равнопеременного движения можно найти как первую производную от вектора скорости по времени или как вторую производную от вектора перемещения по времени:
Если тело движется прямолинейно вдоль оси ОХ прямолинейной декартовой системы координат, совпадающей по направлению с траекторией тела, то проекция вектора скорости на эту ось определяется формулой:
Знак «-» (минус) перед проекцией вектора ускорения относится к равнозамедленному движению. Аналогично записываются уравнения проекций вектора скорости на другие оси координат.
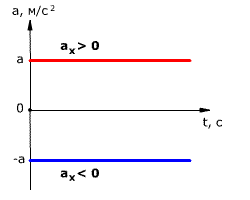
Так как при равнопеременном движении ускорение является постоянным (a = const), то график ускорения – это прямая, параллельная оси 0t (оси времени, рис. 1.15).
Рис. 1.15. Зависимость ускорения тела от времени.
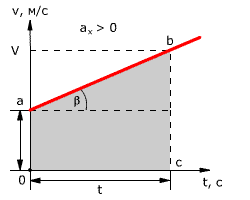
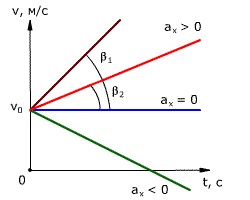
Зависимость скорости от времени – это линейная функция, графиком которой является прямая линия (рис. 1.16).
Рис. 1.16. Зависимость скорости тела от времени.
График зависимости скорости от времени (рис. 1.16) показывает, что
При этом перемещение численно равно площади фигуры 0abc (рис. 1.16).
Площадь трапеции равна произведению полусуммы длин её оснований на высоту. Основания трапеции 0abc численно равны:
Высота трапеции равна t. Таким образом, площадь трапеции, а значит, и проекция перемещения на ось ОХ равна:
В случае равнозамедленного движения проекция ускорения отрицательна и в формуле для проекции перемещения перед ускорением ставится знак «–» (минус).
Общая формула для определения проекции перемещения:
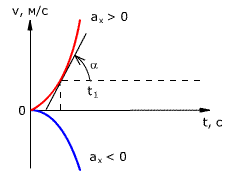
График зависимости скорости тела от времени при различных ускорениях показан на рис. 1.17. График зависимости перемещения от времени при v0 = 0 показан на рис. 1.18.
Рис. 1.17. Зависимость скорости тела от времени для различных значений ускорения.
Рис. 1.18. Зависимость перемещения тела от времени.
Скорость тела в данный момент времени t1 равна тангенсу угла наклона между касательной к графику и осью времени v = tg α, а перемещение определяют по формуле:
Если время движения тела неизвестно, можно использовать другую формулу перемещения, решая систему из двух уравнений:
Формула сокращённого умножения разности квадратов поможет нам вывести формулу для проекции перемещения:
Так как координата тела в любой момент времени определяется суммой начальной координаты и проекции перемещения, то уравнение движения тела будет выглядеть следующим образом:
Графиком координаты x(t) также является парабола (как и график перемещения), но вершина параболы в общем случае не совпадает с началом координат. При аx
Видео:ЧК_МИФ_ФМЛ_30 ДВИЖЕНИЕ С ПЕРЕМЕННЫМ УСКОРЕНИЕМСкачать

Движение с переменным ускорением
Движение с переменным ускорением
Здесь 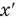
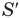
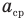
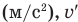
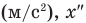
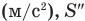
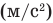
Правило сложения классических скоростей:
Здесь 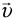
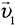
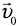
Если из условия задачи следует, что тело начало движение из состояния покоя, например, поезд отошел от станции или автомобиль выехал из пункта А и т. п., то в «Дано:» следует записать, что его начальная скорость 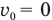
Из сравнения уравнений
следует, что если координата тела х зависит от времени движения t в первой степени, то это равномерное движение, а если координата х зависит от времени 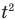
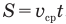
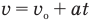
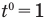
Если вам дано уравнение типа 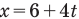
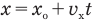
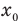
Если вам дано уравнение типа 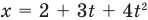
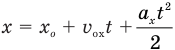
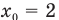
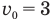
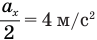
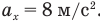
Формулу средней скорости 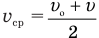
Пути, проходимые телом при равноускоренном движении без начальной скорости, относятся как ряд последовательных нечетных чисел:
Если в условии задачи идет речь о скорости в средней точке пути, то учтите, что это не средняя скорость на всем пути, а мгновенная скорость на середине пути, — она является конечной скоростью для первой половины пути и начальной скоростью для второй половины.
Эта теория со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Возможно вам будут полезны эти страницы:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать

Равномерное и равноускоренное движение
Вы будете перенаправлены на Автор24
Движение, при котором за одинаковые интервалы времени тело проходит неравное расстояние, называют неравномерным (или переменным).
При переменном движении скорость тела с течением времени меняется, по этой причине для характеристики подобного перемещения применяются определения средней и моментальной скоростей.
Средней скоростью переменного движения $v_$ называют векторную величину, равную отношению перемещения тела $s$ к промежутку времени $t$, в течении которого оно совершило перемещение:
Переменное перемещение внедряет в процесс только лишь тот интервал времени, для которого эта скорость установлена. Мгновенной скоростью является скорость, какой тело обладает в определенный период времени (и значит, в конкретной точке траектории). Мгновенная скорость $v$ является пределом, к которому устремляется средняя скорость точки $v_$, в то время как промежуток времени движения точки стремится к 0:
Из курса математики известно, что предел отношения приращения функции к приращению аргумента, когда последний стремится к 0 (если этот порог существует), выступает главной производной этой функции по данному аргументу.
Изучим, как скатывается шарик с наклонной плоскости. Шар перемещается неровно: пути, проходимые им за последовательные одинаковые интервалы периода, увеличиваются. Таким образом, темп передвижения шарика возрастает. Перемещение объекта, скатывающегося с косой плоскости, считается классическим примером прямолинейного равноускоренного перемещения.
Рассмотрим определение равноускоренного движения.
Прямолинейным равноускоренным движением именуют прямолинейное перемещение, при котором скорость тела за любые одинаковые интервалы времени меняется на одну и ту же величину.
Прямо равноускорено способен передвигаться, к примеру, транспорт в период разгона. Но необычным может представиться в таком случае, то что во время торможения машина также способна передвигаться прямолинейно равноускорено! Так как в определении равноускоренного перемещения речь никак не идет не о росте стремительности, а только лишь об изменении скорости.
Готовые работы на аналогичную тему
Суть в том, что представление ускорения в физике обширнее, нежели в обыденном понимании. В повседневной речи под ускорением подразумевают как правило только лишь повышение быстроты. Мы в физике станем говорить, то что тело перемещается с ускорением постоянно, если быстрота тела меняется любым способом (возрастает либо снижается согласно модулю, меняется согласно направленности и т.п.).
Может возникнуть вопрос: по какой причине мы уделяем внимание непосредственно прямолинейному равноускоренному перемещению? Забегая немножко вперед, скажем, что с этим перемещением мы будем часто иметь дело при рассмотрении законов механики.
Напомним, что под воздействием стабильной силы тело перемещается прямо равноускорено. (В случае если первоначальная скорость тела равна нулю либо ориентирована по линии воздействия силы.) А в многочисленных задачах из сферы механики рассматривается непосредственно такая ситуация, в которой применяются уравнения прямолинейного равноускоренного движения, формулы конечной скорости и формулы пути без времени.
Видео:Уравнение движения с постоянным ускорением | Физика 10 класс #6 | ИнфоурокСкачать

Равноускоренное движение тела
Равноускоренное движение — это перемещение тела, при каком его скорость за всевозможные одинаковые интервалы времени меняется (способна расти либо снижаться) одинаково.
Равноускоренное перемещение никак не обладает равной скоростью в течении всего пути прохождения. В этом случае имеется убыстрение, что отвечает за непрерывное повышение скорости. Ускорение перемещения остается постоянным, а темп регулярно и одинаково увеличивается.
Кроме равноускоренного имеется также равнозамедленное перемещение, где модуль темп одинаково уменьшается. Таким образом, равноускоренное перемещение способно проходить в некоторых измерениях. Оно бывает:
В случае первого — перемещение осуществляется по одной оси местоположение. В случае второго могут добавляться и прочие замеры.
Видео:Прямолинейное равноускоренное движение. Ускорение | Физика 9 класс #5 | ИнфоурокСкачать

Ускорение тела
Применять формулы перемещений при равноускоренном движении, а также формулы ускорения без времени возможно в абсолютно различных плоскостях. К примеру, с целью расчета падения жестких тел в свободном падении, места падения. В частности, для различных точных и геометрических расчетов.
Исходя из противопоставления равномерному перемещению, неравномерное — это движение с разной скоростью согласно каждой траектории. В чем его особенность? Это неравномерное передвижение, но оно «равно ускоряется».
Ускорение мы ассоциируем с увеличением скорости. Так как она ускоряется одинаково, получается равное увеличение скорости. Как понять, скорость равно увеличивается или нет? Нам нужно засечь время, оценить скорость через одинаковый промежуток времени, используя формулы ускорения при равноускоренном движении.
Например, автомобиль начал движение, за первые 2 сек он развил скорость до 10 м/с, за последующие 2 сек 20 м/с. Еще через 2 сек он уже едет со скоростью 30 м/с. Каждые 2 секунды темп возрастает и каждый раз на 10 м/с.
Такое передвижение и является равноускоренным. Ускорением называется величина, определяющая, насколько каждый раз увеличивается скорость. Кроме этого необходимо обратить внимание на формулу скорости при равноускоренном движении.
Перемещение с убывающей скоростью — замедленное передвижение. Однако физики каждое перемещение с изменяющейся быстротой называют ускоренным перемещением. Трогается ли автомобиль с участка (темп увеличивается), либо притормаживает — скорость снижается, в каждом случае он перемещается с ускорением.
Быстроту изменения скорости характеризует ускорение. Это число, на которое меняется скорость за каждую секунду. Если ускорение точки по модулю большое, значит точка стремительно набирает скорость (при разгоне) или быстро сбрасывает ее (при торможении). Ускорение $a$ — это физическая векторная величина, которая равна отношению перемены скорости $delta V$ к промежутку времени $delta t$, за которое оно произошло
Видео:Скорость и перемещение при прямолинейном равноускоренном движении. 9 класс.Скачать

Равномерное движение
Механическое передвижение, при котором тело за всевозможные одинаковые интервалы времени проходит одну и ту же дистанцию является равномерным. При равномерном перемещении значение скорости точки остаётся стабильной (формула равномерного и равноускоренного движения).
- $υ$– скорость равномерного движения (м/с)
- $l$– пройденный телом путь (м)
- $ delta t$– интервал времени движения (с)
Равномерное перемещение присутствует, если скорость предмета остается равной в каждом интервале пройденного пути, к этом случае период прохождения различных двух одинаковых участков будет одинаково.
В случае если перемещение является не только лишь равномерным, а и прямолинейным, в таком случае путь тела одинаковый с модулем передвижения. По этой причине, воспользовавшись аналогией с предшествующей формулой равноускоренного движения, в физике определяют скорость равномерного прямолинейного перемещения:
- $ vec$ — скорость равно прямолинейного движения, м/с
- $ vec
$ — перемещение тела, м - $$ — интервал времени движения, с
Скорость равномерного прямолинейного движения является вектором, так как перемещение – величина векторная. А значит, имеет не только числовое значение, но и пространственное направление.
Равноускоренное перемещение отлично от равномерного тем, что быстрота в этом перемещении регулярно и одинаково увеличивается, вплоть до конкретного предела. В равномерном же перемещении скорость не изменяется ни в коем случае, другим образом подобное перемещение никак не станет называться равномерным.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 08 08 2021
📸 Видео
Физика - перемещение, скорость и ускорение. Графики движения.Скачать

Прямолинейное равнопеременное движение, ускорение. 9 класс.Скачать

Урок 106. Реактивное движениеСкачать

Уравнение Мещерского, формула ЦиолковскогоСкачать

Физика - уравнения равноускоренного движенияСкачать

РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ физика 9 ПерышкинСкачать

Урок 12. Равномерное прямолинейное движениеСкачать

Ускорение. Движение с постоянным ускорением. Единица ускорения | Физика 10 класс #5 | ИнфоурокСкачать

Уравнение равномерного движения. Решение задач по теме.Скачать

Равномерное прямолинейное движение - физика 9Скачать

Прямолинейное движение с переменным ускорениемСкачать

Физика 8 класс (Урок№28 - Скорость при неравном. движ. Ускорение и скорость при равноперем. движ.)Скачать

Формула ЦиолковскогоСкачать

01 Движение с постоянным и переменным ускорениемСкачать

МЕХАНИЧЕСКОЕ ДВИЖЕНИЕ: Равномерное движение и Прямолинейное Движение || Скорость — Физика 7 классСкачать