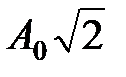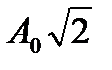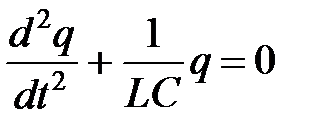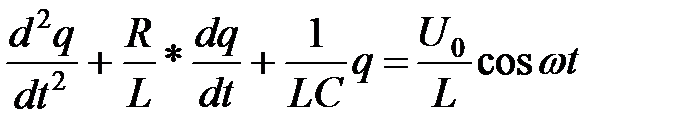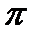Уравнение движения пружинного маятника 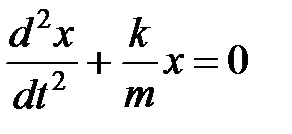является дифференциальным уравнением свободных затухающих (7 видео)

Колебания и волны

Уравнение движения пружинного маятника является дифференциальным уравнением .

свободных незатухающих колебаний

Уравнение движения пружинного маятника 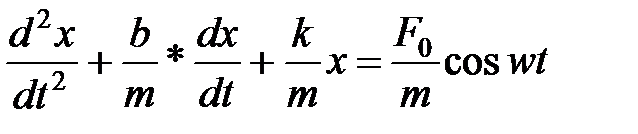является дифференциальным уравнением .

При сложении двух гармонических колебаний одного направления с одинаковыми периодами и равными амплитудами результирующее колебание имеет такую же амплитуду, что и складываемые колебания. При этом разность фаз исходных колебаний равна .

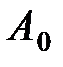
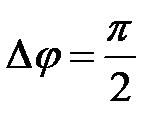
Складываются два гармонических колебания одного направления с одинаковыми частотами и равными амплитудами . При разности фаз амплитуда результирующего колебания равна .

Складываются два гармонических колебания одного направления с одинаковыми периодами. Результирующее колебание имеет максимальную амплитуду при разности фаз, равной .

Складываются два гармонических колебания одного направления с одинаковыми периодами и равными амплитудами A_0. При разности фаз амплитуда результирующего колебания равна .

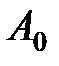
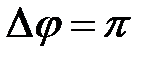
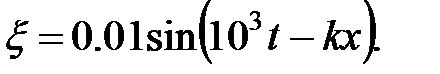
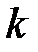
Уравнение плоской синусоидальной волны, распространяющейся вдоль оси ОХ со скоростью 500 м/с, имеет вид Волновое число (в м -1 ) равно .

Уравнение плоской синусоидальной волны, распространяющейся вдоль оси ОХ, имеет вид 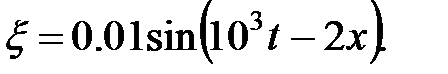Длина волны (в м) равна .

3,14

Уравнение плоской синусоидальной волны, распространяющейся вдоль оси ОХ, имеет вид 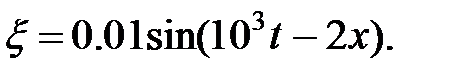Период (в мс) равен .

6,28

Уравнение плоской синусоидальной волны, распространяющейся вдоль оси ОХ, имеет вид 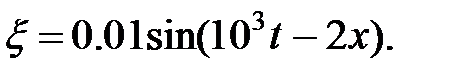Тогда скорость распространения волны (в м/с) равна .

500

Уравнение плоской синусоидальной волны, распространяющейся вдоль оси ОХ со скоростью 500 м/с, имеет вид 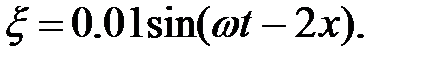Циклическая частота (в с -1 ) равна .

1000

Свободные незатухающие колебания заряда конденсатора в колебательном контуре описываются уравнением.

Вынужденные колебания заряда конденсатора в колебательном контуре описываются уравнением .

Уравнение движения пружинного маятника 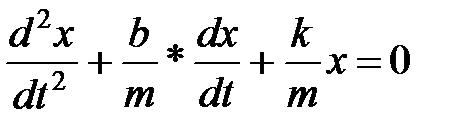Является дифференциальным уравнением .

свободных затухающих колебаний

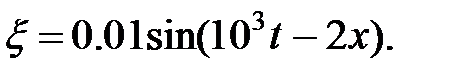
500

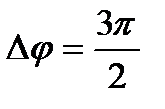
Складываются два гармонических колебания одного направления с одинаковыми периодами и равными амплитудами А . При разности фаз амплитуда результирующего колебания равна .

Складываются два гармонических колебания одного направления с одинаковыми периодами. Результирующее колебание имеет минимальную амплитуду при разности фаз, равной .

Если увеличить в 2 раза объемную плотность энергии и при этом увеличить в 2 раза скорость распространения упругих волн, то плотность потока энергии .

увеличится в 4 раза

На рисунках изображены зависимости от времени координаты и скорости материальной точки, колеблющейся по гармоническому закону. Циклическая частота колебаний точки равна .

На рисунках изображены зависимости от времени координаты и ускорения материальной точки, колеблющейся по гармоническому закону. Циклическая частота колебаний точки равна .

Складываются два гармонических колебания одного направления с одинаковыми периодами. Результирующее колебание имеет минимальную амплитуду при разности фаз, равной .

Сейсмическая упругая волна, падающая со скоростью 5,6 км/с под углом 45° на границу раздела между двумя слоями земной коры с различными свойствами, испытывает преломление, причем угол преломления равен 30°. Во второй среде волна будет распространяться со скоростью .

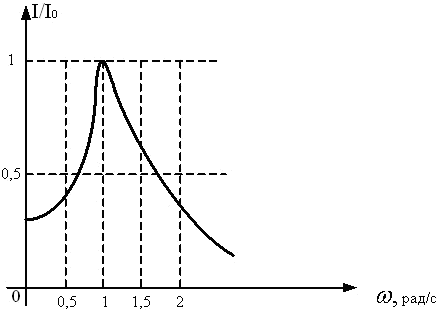
На рисунке представлена зависимость относительной амплитуды колебаний силы тока в катушке индуктивностью1 мГн, включенной в идеальный колебательный контур. Емкость конденсатора этого контура равна .

На рисунках изображены зависимости от времени скорости и ускорения материальной точки, колеблющейся по гармоническому закону. Циклическая частота колебаний точки равна .

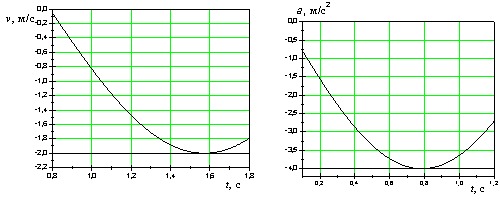Уравнение движения пружинного маятника является дифференциальным уравнением свободных затухающих

2 с -1

Сейсмическая упругая волна, падающая под углом 45° на границу раздела между двумя слоями земной коры с различными свойствами, испытывает преломление, причем угол преломления равен 30°. Во второй среде волна распространяется со скоростью 4,0 км/с. В первой среде скорость волны была равна .

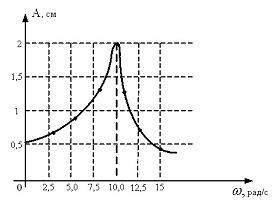
На рисунке представлена зависимость амплитуды колебаний груза на пружине с жесткостью k=10 Н/м от частоты внешней силы. Масса колеблющегося груза равна .

Если увеличить в 2 раза объемную плотность энергии и при этом уменьшить в 2 раза скорость распространения упругих волн, то плотность потока энергии .

Видео:Урок 92 (осн). Колебательное движение. МаятникиСкачать

Вывод дифференциального уравнения затухающих колебаний

Выведем дифференциальное уравнение свободных затухающих колебаний пружинного маятника (упругого осциллятора). На колебательную систему при колебаниях действуют упругая сила F _vnp и сила трения F _тр, равные

где г — постоянный положительный коэффициент пропорциональности, называемый коэффициентом сопротивления.

Знак “минус “ говорит о том, что сила трения направлена всегда в сторону, противоположную направлению скорости движения тела. По второму закону Ньютона или отсюда

Введём обозначения: со₀ = _- циклическая (круговая) частота

свободных незатухающих колебаний пружинного маятника, когда нет потерь энергии, её называют собственной частотой системы.

Обозначим отношение —= 2/?, р =— = const >0

С учётом введённых обозначений уравнение (18.60) примет вид

Формула (19.61) является дифференциальным уравнением свободных механических затухающих колебаний пружинного маятника.

Рассмотрим свободные затухающие колебания в электрическом колебательном контуре, содержащем, кроме конденсатора, катушки индуктивности, так же и активное сопротивление, которое складывается из сопротивления резистора, проводов и катушки индуктивности (рис. 187).

Запишем закон Ома для колебательного контура, т. е. неоднородного участка электрической цепи 1 L — R — 2

где U = — Д — разность потенциалов на обкладках 1, 2 конденсатора,

f, = L-— — ЭДС самоиндукции.

Сила J электрического тока в колебательном контуре равна

Знак “ минус “говорит о том, что положительному направлению электрического тока соответствует убывание электрического положительного заряда q на первой обкладке конденсатора. Тогда уравнение (19.673 запишется r чипе

Уравнение (19.63) дифференциальное уравнение свободных затухающих колебаний электрического заряда q в колебательном контуре.

Из сравнения уравнений (19.63) и (19.61) следует, что дифференциальные уравнения затухающих механических и электрических колебаний аналогичны друг другу. Эти уравнения запишем в общем виде

где S — колеблющаяся физическая величина.

Для пружинного маятника физическая величина S означает смещение тела относительно положения равновесия (S = х), а для колебательного контура под S понимают электрический заряд q обкладки конденсатора (S = ц).

Решение дифференциального уравнения (19.64) имеет вид

где S о,max — начальная амплитуда колебаний величины S,

(р₀ — начальная фаза колебаний.

со — циклическая частота затухающих колебаний, она равна or = col — 0 1 ?

где со₀ — собственная частота колебаний колебательной системы.

Начальная амплитуда S ₀.тах и начальная фаза ^ ^ и подставить их в дифференциальное

уравнение (19.63). В результате в правой части уравнения получим нуль. Так как

то закон изменения со временем амплитуды затухающих колебаний имеет вид

где А₀ — начальная амплитуда колебаний (Aq = So,_max), е — основание натурального логарифма.

Из уравнения (19.66) видно, что амплитуда А (?) затухающих колебаний убывает со временем по экспоненциальному закону и тем быстрее, чем больше величина коэффициента затухания /?. График зависимости амплитуды затухающих колебаний физической величины S со временем ? приведён на рис. 188.

Затухание колебаний нарушает их периодичность. Колебания не являются периодическим процессом и к ним не применимо понятие периода или частоты. Но если затухание колебаний мало, то можно условно использовать понятие периода, как интервала времени между двумя последующими максимумами или минимумами колеблющейся физической величины S. Но максимальное значение величины S, достигаемое в некоторый момент времени ?, в дальнейшем никогда не повторяется.

При затухающих колебаниях величина S через равные интервалы времени Т достигает максимального, минимального значения и обращается в нуль. Интервал времени Т между двумя последующими максимумами или минимумами колеблющейся величины S, называется условным периодом, равным где со — условная циклическая частота затухающих колеЬаний, со₀ — собственная частота колебаний.

Циклическая частота со затухающих колебаний за счёт потерь энергии меньше собственной частоты со₀ колебаний. Свободные затухающие колебания не являются гармоническими. При малом затухании их можно рассматривать, как квазигармонические с частотой со и амплитудой А, убывающей со временем по экспоненциальному закону.

Рассмотрим изменение полной энергии W _пол колебательной системы для затухающих колебаний. Полная энергия W _пол пружинного маятника, совершающего механические колебания, равна

а полная энергия колебательного контура

Из уравнений (19.68) и (19.67) следует, что полная энергия колебательной системы пропорциональна квадрату амплитуды и при затухающих колебаниях со внеменем убывает по закону

где W „о. — полная энергия системы в начальный момент времени (t = 0).

Видео:Математические и пружинные маятники. 11 класс.Скачать

Свободные колебания пружинного маятника. Общие сведения

Цель работы. Ознакомиться с основными характеристиками незатухающих и затухающих свободных механических колебаний.

Задача. Определить период собственных колебаний пружинного маятника; проверить линейность зависимости квадрата периода от массы; определить жесткость пружины; определить период затухающих колебаний и логарифмический декремент затухания пружинного маятника.

Приборы и принадлежности. Штатив со шкалой, пружина, набор грузов различной массы, сосуд с водой, секундомер.

1. Свободные колебания пружинного маятника. Общие сведения

Колебаниями называются процессы, в которых периодически изменяется одна или несколько физических величин, описывающих эти процессы. Колебания могут быть описаны различными периодическими функциями времени. Простейшими колебаниями являются гармонические колебания – такие колебания, при которых колеблющаяся величина (например, смещение груза на пружине) изменяется со временем по закону косинуса или синуса. Колебания, возникающие после действия на систему внешней кратковременной силы, называются свободными.

Рассмотрим одну из простейших колебательных систем – пружинный маятник, представляющий собой груз массой m, подвешенный на абсолютно упругой пружине с коэффициентом жесткости k
(рис. 1). Пусть l0 – длина пружины без подвешенного к ней груза. При подвешивании груза под действием силы тяжести пружина растянется на x1 так, что маятник будет находиться в положении равновесия вследствие равенства модулей силы тяжести mg и упругой силы Fупр: mg = kx1, стремящейся вернуть груз в положение равновесия (полагается, что деформации пружины идеально упругие и подчиняются закону Гука).

Если груз вывести из положения равновесия, отклонив на величину x, то сила упругости возрастает: Fупр = – kx2= – k(x1 + x). Дойдя до положения равновесия, груз будет обладать отличной от нуля скоростью и пройдет положение равновесия по инерции. По мере дальнейшего движения будет увеличиваться отклонение от положения равновесия, что приведет к возрастанию силы упругости, и процесс повторится в обратном направлении. Таким образом, колебательное движение системы обусловлено двумя причинами: 1) стремлением тела вернуться в положении равновесия и 2) инерцией, не позволяющей телу мгновенно остановиться в положении равновесия. В отсутствии сил трения колебания продолжались бы сколь угодно долго. Наличие силы трения приводит к тому, что часть энергии колебаний переходит во внутреннюю энергию и колебания постепенно затухают. Такие колебания называются затухающими.

Незатухающие свободные колебания

Сначала рассмотрим колебания пружинного маятника, на который не действуют силы трения – незатухающие свободные колебания. Согласно второму закону Ньютона c учетом знаков проекций на ось X

(1)

Из условия равновесия смещение, вызываемое силой тяжести: . Подставляя в уравнение (1), получим: . Разделив правую и левую часть этого уравнения на m и принимая, что a = d2x/dt2, получим дифференциальное уравнение

. (2)

Это уравнение называется дифференциальным уравнением гармонических колебаний пружинного маятника. Из этого уравнения следует, что после прекращения внешнего воздействия, приводящего к первоначальному отклонению системы от положения равновесия, движение груза обусловлено только действием упругой силы (сила тяжести вызывает постоянное смещение).

Общее решение однородного дифференциального уравнения второго порядка (2) имеет вид

. (3)

Данное уравнение называется уравнением гармонических колебаний. Наибольшее отклонение груза от положения равновесия А0 называется амплитудой колебаний. Величина , стоящая в аргументе косинуса, называется фазой колебания. Постоянная φ0 представляет собой значение фазы в начальный момент времени (t = 0) и называется начальной фазой колебаний. Величина

(4)

есть круговая или циклическая частота собственных колебаний, связанная с периодом колебаний Т соотношением . Период колебаний определяется

. (5)

Рассмотрим свободные колебания пружинного маятника при наличии силы трения (затухающие колебания). В простейшем и вместе с тем наиболее часто встречающемся случае сила трения пропорциональна скорости υ движения:

где r – постоянная, называемая коэффициентом сопротивления. Знак минус показывает, что сила трения и скорость имеют противоположные направления. Уравнение второго закона Ньютона в проекции на ось Х при наличии упругой силы и силы трения

Данное дифференциальное уравнение с учетом υ = dx/dt можно записать

, (8)

где – коэффициент затухания; – циклическая частота свободных незатухающих колебаний данной колебательной системы, т. е. при отсутствии потерь энергии (β = 0). Уравнение (8) называют дифференциальным уравнением затухающих колебаний.

Чтобы получить зависимость смещения x от времени t, необходимо решить дифференциальное уравнение (8). В случае малых затуханий () решение уравнения можно записать следующим образом:

, (9)

где А0 и φ0 – начальная амплитуда и начальная фаза колебаний;
– циклическая частота затухающих колебаний при ω >> ω ≈ ω0.

Движение груза в этом случае можно рассматривать как гармоническое колебание с частотой ω и переменной амплитудой, меняющейся по закону:

. (10)

На графике функции (9), рис. 2, пунктирными линиями показано изменение амплитуды (10) затухающих колебаний.

Рис. 2. Зависимость смещения х груза от времени t при наличии силы трения

Для количественной характеристики степени затухания колебаний вводят величину, равную отношению амплитуд, отличающихся на период, и называемую декрементом затухания:

. (11)

Часто используют натуральный логарифм этой величины. Такой параметр называется логарифмическим декрементом затухания:

. (12)

Если за время t‘ амплитуда уменьшается в n раз, то из уравнения (10) следует, что

. (13)

Отсюда для логарифмического декремента получаем выражение

. (14)

Если за время t‘ амплитуда уменьшается в е раз (е = 2,71 – основание натурального логарифма), то система успеет совершить число колебаний

. (15)

Следовательно, логарифмический декремент затухания – величина, обратная числу колебаний, совершаемых за то время, за которое амплитуда уменьшается в е раз. Чем больше θ, тем быстрее происходит затухание колебаний.

2. Методика эксперимента и экспериментальная установка

Рис. 3. Схема установки

Установка состоит из штатива 1 с измерительной шкалой 2. К штативу на пружине 3 подвешиваются грузы 4 различной массы. При изучении затухающих колебаний в задании 2 для усиления затухания используется кольцо 5, которое помещается в прозрачный сосуд 6 с водой.

В задании 1 (выполняется без сосуда с водой и кольца) в первом приближении затуханием колебаний можно пренебречь и считать гармоническими. Как следует из формулы (5) для гармонических колебаний зависимость T 2 = f (m) – линейная, из которой можно определить коэффициент жесткости пружины k по формуле

, (16)

где – угловой коэффициент наклона прямой T 2 от m.

Задание 1. Определение зависимости периода собственных колебаний пружинного маятника от массы груза.

1. Определить период колебаний пружинного маятника при различных значениях массы груза m. Для этого с помощью секундомера для каждого значения m трижды измерить время t полных n колебаний (n ≥10) и по среднему значению времени вычислить период . Результаты занести в табл. 1.

2. По результатам измерений построить график зависимости квадрата периода T2 от массы m. Из углового коэффициента графика определить жесткость пружины k по формуле (16).

Результаты измерений для определения периода собственных колебаний

, с