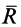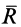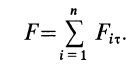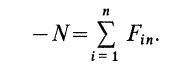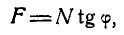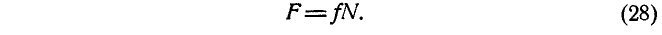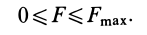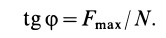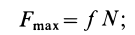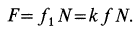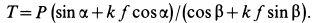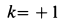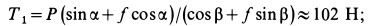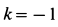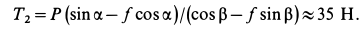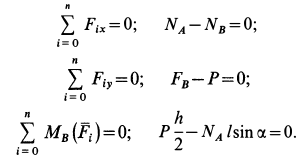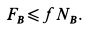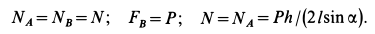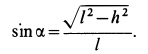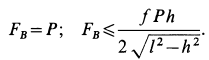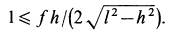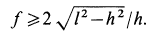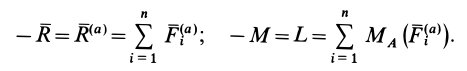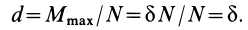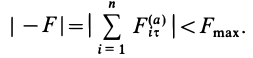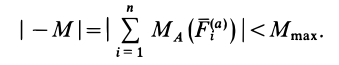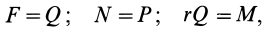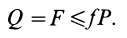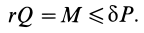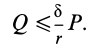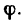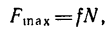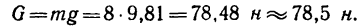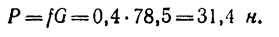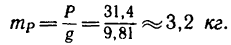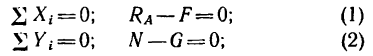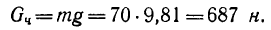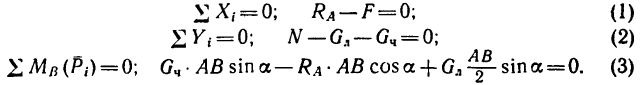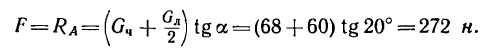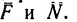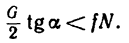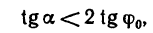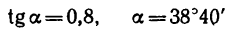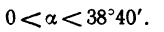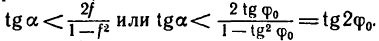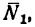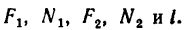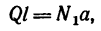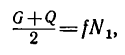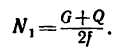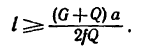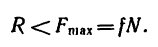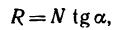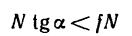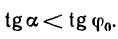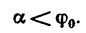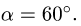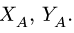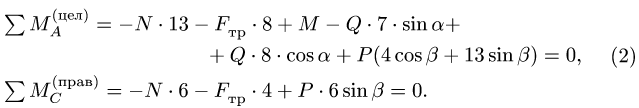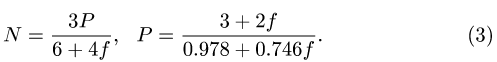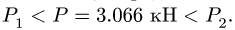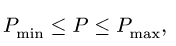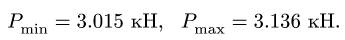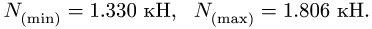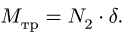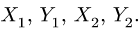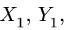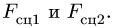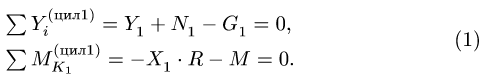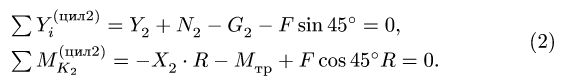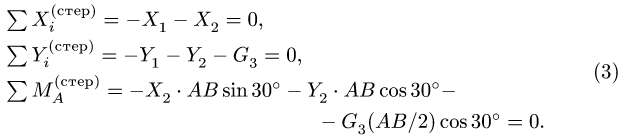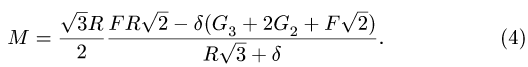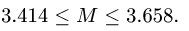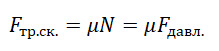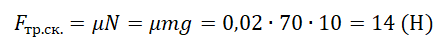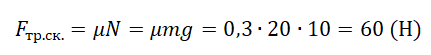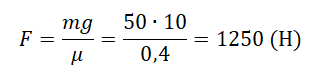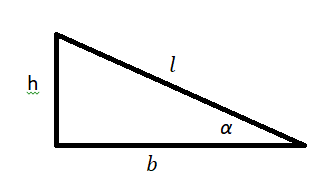- Трение — основные понятия, законы и зависимости
- Понятие трения
- Трение скольжения
- 1-й закон Кулона
- 2-й закон Кулона
- 3-й закон Кулона
- Трение на наклонной поверхности
- Трение в теоретической механике
- Трение скольжения
- Первый закон трения
- Задача №1
- Задача №2
- Законы Кулона
- Угол и конус трения
- Равновесие тела на шероховатой поверхности
- Пример 1.
- Пример 2.
- Трение качения
- Равновесие с учетом сил трения
- Задача №3
- Задача №4
- Задача №5
- Задача №6
- Задача №7
- Задача №8
- Задача №9
- Равновесие при наличии трения
- Задача №10
- Трение качения
- Задача №11
- Сила трения
- теория по физике 🧲 динамика
- Трение скольжения
- Трение покоя
- Описание движения тел с учетом сил трения
- Движение тела по горизонтальной плоскости
- Равноускоренное движение по горизонтали, сила тяги параллельная плоскости
- Равнозамедленное движение по горизонтали, сила тяги параллельная плоскости
- Ускоренное движение по горизонтали, сила тяги направлена под углом к горизонту (вверх)
- Ускоренное движение по горизонтали, сила тяги направлена под углом к горизонту (вниз)
- Движение тела по вертикальной плоскости
- Тело прижали к вертикальной плоскости и удерживают
- Тело поднимается под действием силы тяги, направленной под углом к вертикали
- Движение тела по наклонной плоскости
- Движение вниз без трения
- Тело покоится на наклонной плоскости
- Тело удерживают на наклонной плоскости
- Равноускоренное движение вверх с учетом силы трения
- Равномерное движение вверх с учетом силы трения
- 📹 Видео
Видео:Урок 39 (осн). Сила трения. Коэффициент тренияСкачать

Трение — основные понятия, законы и зависимости
Понятие трения
Как известно, в природе не существует абсолютно гладких и абсолютно твердых тел, поэтому при перемещении одного тела по поверхности другого возникает сопротивление, которое называется трением.
Трение – явление сопротивления относительному перемещению, возникающее между двумя телами в зонах соприкасания поверхностей по касательной к ним.
Трение – явление чрезвычайно распространенное в природе и имеющее большое значение. При этом оно может выполнять и полезные, и вредные функции. На трении основана работа фрикционных и ременных передач, муфт, наклонных транспортеров, прокатных станов, тормозных устройств и т. п.
Трение обеспечивает сцепление тел с земной поверхностью и, следовательно, работу машин, тракторов и другой транспортной самоходной техники. При отсутствии трения мы не могли бы ходить по земле, поскольку наши ноги скользили бы и разъезжались в разные стороны, как у неумелого конькобежца на гладком льду.
Наряду с полезными свойствами, трение является во многих устройствах и механизмах вредным сопротивлением, которое отнимает львиную долю мощности и энергии у машин. Для уменьшения трения в механизмах конструкторам приходится применять различные приемы и способы, чтобы снизить непродуктивные потери энергии.
Трение классифицируют по характеру движения, в результате которого оно возникает. Различают трение покоя, трение скольжения, трение качения и трение качения с проскальзыванием . Очевидно, что последний из перечисленных видов трения является комбинацией трения скольжения и трения качения.
Трением покоя называется трение двух тел при начальном (бесконечно малом) относительном перемещении в момент перехода от состояния покоя к состоянию относительного движения. Это явление можно объяснить шероховатостью поверхностей соприкасающихся тел, а также их деформацией, вызванной взаимным давлением друг на друга.
Кроме того, при таком взаимном давлении (контакте) между телами, на их поверхностях возникают силы молекулярного сцепления. Для того, чтобы начать взаимное перемещение тел, необходимо преодолеть все эти факторы, обуславливающие трение покоя.
Трением движения называется трение двух тел, находящихся в относительном движении. Рассмотрим основные виды трения в зависимости от характера относительного движения тел.
Трение скольжения
Трением скольжения называется трение движения, при котором скорости тел в точке касания различны по значению и (или) направлению.

Трение характеризуется силой трения.
Сила трения есть сила сопротивления относительному перемещению двух тел при трении.
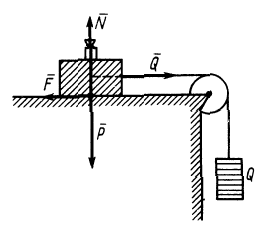
Рассмотрим тело, лежащее на горизонтальной шероховатой плоскости (см. рисунок 1) .
Сила тяжести G уравновешивается нормальной реакцией плоской поверхности N . Если к телу приложить небольшую движущую силу P , то оно не придет в движение, так как эта сила будет уравновешиваться силой трения Fтр , которая является, таким образом, составляющей реакции опорной плоскости, направленной вдоль плоскости в противоположную перемещению сторону.
Если постепенно увеличивать сдвигающую силу P , то до определенного ее значения тело будет оставаться в покое, а затем придет в движение.
Очевидно, что сила трения в состоянии покоя может изменяться в зависимости от степени микросмещения может изменяться от нуля до какого-то максимального значения F max тр , причем в промежутке между нулем и максимальным значением сила трения Fтр по модулю всегда равна сдвигающей силе P .
Максимальное значение сила трения покоя имеет в момент начала относительного движения. Это значение называется наибольшей силой трения покоя или просто силой трения покоя.
Сила трения всегда направлена в сторону, противоположную направлению относительного движения тела.
В XVIII веке французские ученые Гийом Атонтон (1663-1705) , а затем Шарль Огюстен Кулон (1736-1806) провели фундаментальные исследования в области трения, и на основе их сформулировали три основных закона трения скольжения, которые обычно называют законами Кулона.
1-й закон Кулона
Cила трения не зависит от величины площади трущихся поверхностей.
Первый закон можно объяснить с помощью следующих умозаключений. Если площадь трущихся поверхностей увеличится, то увеличится и количество сцепляющихся неровностей, но уменьшится давление на опорную поверхность, которое обратно пропорционально площади контакта тел. Поэтому сопротивление относительному перемещению останется прежним.
2-й закон Кулона
Максимальная сила трения прямо пропорциональна нормальной составляющей внешних сил, действующих на поверхности тела.
Второй закон Кулона говорит о том, что если увеличится нормальная составляющая внешних сил, действующих на поверхности тела (иначе говоря, увеличится сила нормального давления или реакции), то во столько же раз возрастет максимальная сила трения.
Поскольку зависимость эта прямо пропорциональная, можно выделить коэффициент, характеризующий ее пропорциональность. Этот коэффициент называется коэффициентом трения скольжения , и определяется он, как отношение силы трения Fтр к нормальной составляющей N внешних сил, действующих на поверхности тела. Обозначается коэффициент трения скольжения f .
При наибольшей силе трения покоя коэффициент трения называют коэффициентом сцепления .
В результате второй закон трения скольжения можно сформулировать так: сила трения равна коэффициенту трения скольжения, умноженному на силу нормального давления или реакции.
Очевидно, что коэффициент трения скольжения – величина безразмерная.
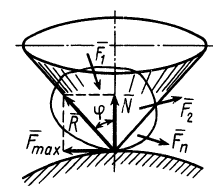
Нормальная реакция N опорной поверхности и сила трения Fтр дают равнодействующую R , которая называется полной реакцией опорной поверхности (см. рисунок 2) .
Полная реакция R составляет с нормалью к опорной поверхности некоторый угол. Максимальное значение этого угла (достигает в момент начала относительного движения) называется углом трения и обозначается φ .
Из рисунка 2 очевидно, что
т. е. коэффициент трения скольжения равен тангенсу угла трения.
Если коэффициент трения скольжения одинаков для всех направлений движения, то множество (геометрическое место) полных реакций образует круговой конус, который называется конусом трения (см. рисунок 2) .
Если для разных направлений движения коэффициент трения неодинаков (например, при скольжении по дереву вдоль волокон и поперек волокон), то конус трения будет некруговым (несимметричным).
Свойство конуса трения заключается в том, что для равновесия тела, лежащего на шероховатой поверхности, равнодействующая приложенных к нему активных сил должна проходить внутри конуса трения.
Действительно, если равнодействующую P активных сил, приложенных к телу, разложить на составляющие P2 (движущая сила) и P2 (сила нормального давления) , то
По второму закону трения скольжения
Следовательно, при α будет P1 и движение окажется невозможным.
3-й закон Кулона
Сила трения зависит от материала тел, состояния трущихся поверхностей и рода смазки.
Согласно третьему закону трения скольжения, коэффициент трения скольжения зависит от материалов трущихся тел, качества обработки их поверхности (степени шероховатости), рода и температуры смазки. В зависимости от наличия между сопрягаемыми поверхностями слоя смазки трение подразделяется на два вида: трение без смазочного материала (сухое трение) и трение в условиях смазки.
Коэффициент трения скольжения определяют опытным путем; значения его для различных условий приведены в справочниках. Примеры коэффициентов трения для некоторых материалов приведены ниже.
- Металл по металлу без смазки . 0,15. 0,30
- То же, со смазкой . 0,10. 0,18
- Дерево по дереву без смазки . 0,40. 0,60
- Кожа по чугуну без смазки . 0,30. 0,50
- То же, со смазкой . 0,15
- Сталь по льду . 0,02
Коэффициент трения скольжения при движении обычно меньше, чем при покое, и в первом приближении не зависит от скорости относительного перемещения тел.
Методы решения задач статики при наличии трения остаются такими же, как и при отсутствии его, причем в уравнения равновесия обычно вводят максимальные значения сил трения.
Трение на наклонной поверхности
Рассмотрим тело, лежащее на шероховатой наклонной плоскости, составляющей угол α с горизонтальной плоскостью (см. рисунок 3) .

Составляющая G1 стремится сдвинуть тело вдоль наклонной плоскости. Полностью или частично эта составляющая уравновешивается силой трения; согласно второму закону трения скольжения, ее максимальное значение равно:
Fтр = fN = fG cosα , где f – коэффициент трения скольжения тела по наклонной плоскости.
Для того, чтобы тело, лежащее на наклонной плоскости, находилось в равновесии, движущая сила G1 должна быть по модулю равна силе трения Fтр ,т. е.
G sinα = fG cosα или tgα = f = tgφ , откуда следует, что α = φ .
Если угол, который наклонная плоскость составляет с горизонтом, будет равен углу трения, то тело, лежащее на наклонной плоскости ,будет под действием собственной силы тяжести либо равномерно скользить вниз, либо находиться в состоянии покоя (что, собственно, одно и то же).
Для того, чтобы тело, лежащее на наклонной плоскости, заведомо не скользило вниз под действием собственной силы тяжести, должно быть соблюдено условие α .
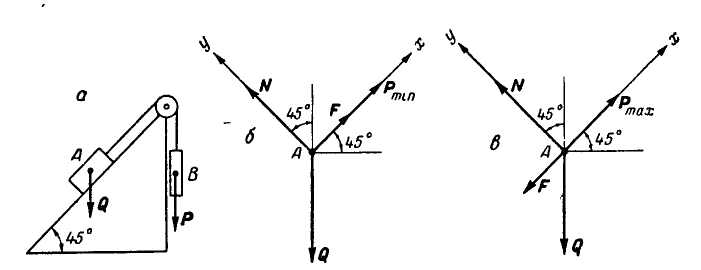
Наклонной плоскостью с переменным углом наклона к горизонту пользуются для экспериментального определения угла трения φ и коэффициента трения f (см. рисунок 4а) .
Определим модуль силы Р , параллельной наклонной плоскости, в случае равномерного перемещения тела вверх по шероховатой наклонной плоскости (см. рисунок 4б) . Спроецируем силы, действующие на тело, на ось x . Составим уравнение равновесия:
ΣX = 0; P – G sinα – Fтр = 0 .
Так как Fтр = fG cosα , то P = G sinα + fG cosα или после преобразований: P = G (tgα + f) .
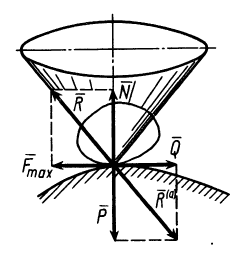
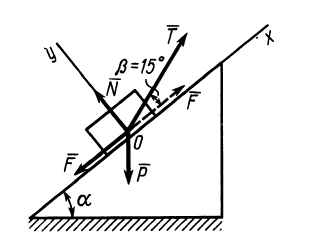
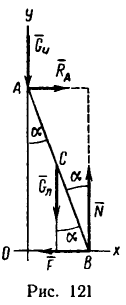
Определим модуль горизонтальной силы Р , которую надо приложить к телу для равномерного перемещения его вверх по шероховатой наклонной плоскости (см. рисунок 5) .
Применим геометрическое условие равновесия плоской системы сил (размерами тела пренебрегаем) и построим замкнутый силовой многоугольник, соответствующий уравнению равновесия:
G + P + N + Fтр = 0 .
Из треугольника abc имеем: P = Gtg(α + φ) .
Этот случай движения имеет место при взаимном перемещении винта и гайки с прямоугольной резьбой, так как резьбу винта можно рассматривать как наклонную плоскость, угол наклона которой равен углу подъема винтовой линии.
Трение в резьбе, имеющей треугольный или трапецеидальный профиль, подобно трению в клинчатом ползуне. Поэтому рассмотрим клинчатый ползун с углом заострения 2β , нагруженный вертикальной силой Q (см. рисунок 6) . Определим силу P , необходимую для равномерного перемещения ползуна вдоль горизонтальных направляющих, если коэффициент трения скольжения равен f .
Составим два уравнения равновесия ползуна:
ΣX = 0; P – 2Fтр = 0;
ΣY = 0; 2Nsinβ – Q = 0 ,
где Fтр – сила трения на каждой грани ползуна; N – нормальная реакция направляющей.
Решая эту систему уравнений и учитывая, что Fтр = fN , получим:
где f’ = f/sinβ – приведенный коэффициент трения.
Соответствующий этому приведенному коэффициенту угол трения обозначим φ’ и назовем приведенным углом трения , тогда:
Очевидно, что f’> f , следовательно, при прочих равных условиях трение в клинчатом ползуне больше трения на плоскости.
Понятие приведенного коэффициента трения условно, так как он изменяется в зависимости от угла заострения клинчатого ползуна.
По аналогии с движением тела вверх по наклонной плоскости под действием горизонтальной силы для равномерного перемещения клинчатого ползуна по направляющим, наклоненным к горизонту под углом α , нужно приложить горизонтальную силу равную
Трение в крепежной метрической резьбе подобно трению клинчатого ползуна с углом заострения 2β = 120˚ , для трапецеидальной резьбы угол 2β = 150˚ .
С трением связано понятие угла естественного откоса — наибольшим углом между наклонной плоскостью и горизонтом, при котором сыпучее тело удерживает свои частицы на поверхности, без их движения (осыпания) вниз. Угол естественного откоса сыпучего тела равен углу трения между его частицами. Этот угол приходится принимать во внимание, например, при различных земляных работах на уклонах и скатах.
Видео:Сила тренияСкачать

Трение в теоретической механике
Содержание:
Трение:
При движении или стремлении двигать одно тело по поверхности другого в касательной плоскости поверхностей соприкосновения возникает сила трения скольжения.
Если одно тело, например цилиндрический каток, катить или стремиться катить по поверхности другого тела, то кроме силы трения скольжения из-за деформации поверхностей тел дополнительно возникает пара сил, препятствующая качению катка. Возникновение силы трения, препятствующей скольжению, иногда называют трением первого рода, а возникновение пары сил, препятствующей качению,— трением второго рода.
Видео:Сила трения покоя и сила трения скольженияСкачать

Трение скольжения
Пусть на тело действует плоская система активных сил и тело находится в равновесии, соприкасаясь с поверхностью другого тела, являющегося связью для рассматриваемого тела. Если поверхности соприкасающихся тел абсолютно гладкие и тела абсолютно твердые, то реакция поверхности связи направлена по нормали к общей касательной в точке соприкосновения и направление реакции в этом случае не зависит от действующих на тело активных сил. От активных сил зависит только числовое значение силы реакции. В действительности абсолютно гладких поверхностей и абсолютно твердых тел не бывает. Все поверхности тел в той или иной степени шероховаты и все тела деформируемы. В связи с этим и сила реакции
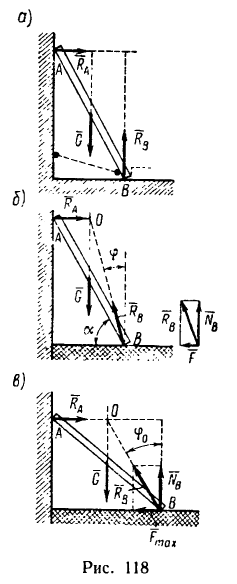
Если силу реакции
В теоретической механике обычно рассматривается только сухое трение между поверхностями тел, т. е. такое трение, когда между ними нет смазывающего вещества. Для сухого трения надо различать трение скольжения при покое или равновесии тела и трение скольжения при движении одного тела по поверхности другого с некоторой относительной скоростью.
При покое сила трения зависит только от активных сил. При выбранном направлении касательной в точке соприкосновения поверхностей тел сила трения вычисляется по формуле
Аналогично, при выбранном направлении нормали нормальная реакция выражается через заданные силы
В 1781 г. Кулон установил основные приближенные законы для сухого трения скольжения. В дальнейшем законы Кулона многократно проверялись другими исследователями. Но эти законы подтверждались в случае, когда поверхности тел не вдавливались друг в друга и шероховатость была не очень велика.
Законы Кулона можно установить на приборе, схема которого дана рис. 59. На этом приборе изменяя вес гири, можно изменять нормальное давление 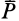
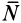
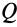
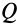
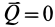
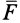
Если силу 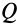
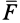
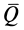
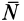
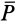
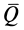
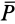
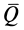
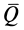
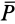
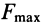
Рис. 59
Трение скольжения:
При решении многих технических вопросов приходится принимать в расчет силы трения. Остановимся на рассмотрении сил трения 1-го рода (скольжения).
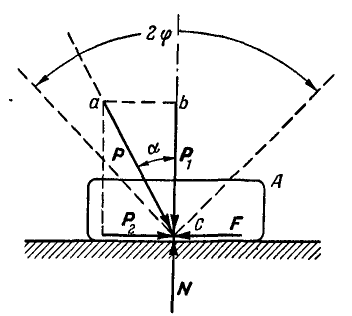
Пусть на тело А (рис. 31), лежащее на горизонтальной негладкой плоскости, действует сила Р под углом а к вертикали. Раскладывая силу Р на две составляющие 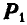
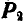
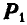
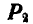
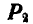
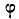

где 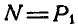
Угол 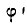
Формула (28) выражает первый закон трения, который формулируется так:
Первый закон трения
1. Сила трения прямо пропорциональна нормальному давлению или реакции связи и направлена в сторону, противоположную относительному перемещению трущихся тел.
Этот закон был установлен опытным путем. Амонтоном-Кулоном и другими исследователями были установлены еще следующие законы:
2. Коэффициент трения зависит от материала и состояния трущихся поверхностей.
3. Коэффициент трения в покое больше коэффициента трения в движении.
4. Коэффициент трения не зависит от величины трущихся поверхностей (можно считать правильным лишь в первом приближении).
5. Коэффициент трения зависит от скорости движения трущихся поверхностей и с увеличением этой скорости уменьшается, приближаясь к некоторой предельной величине.
Обращаясь к рисунку 31, замечаем, что тело А находится в равновесии, если сила Р проходит внутри конуса с углом при вершине С, равным двойному углу трения 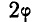
Когда тело А находится еще в покое (рис. 31), то по мере увеличения угла 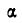
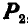
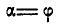
Задача №1
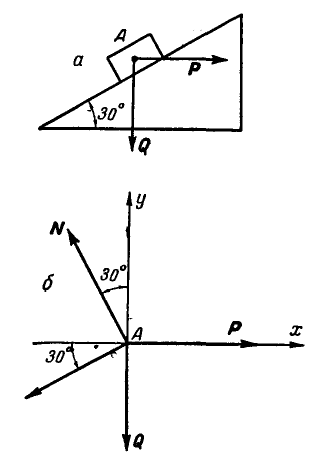
Тело А весом Q=100кГ лежит на шероховатой наклонной плоскости (рис. 32,а). Какую наименьшую горизонтальную силу Р ладо приложить к телу, чтобы оно начало двигаться, если коэффициент трения тела о плоскость f=0,2.
Решение. Рассмотрим равновесие тела А. Помимо горизонтальной силы Р на тело действует сила Q, нормальная реакция N плоскости и сила трения F, направленная параллельно плоскости в обратную сторону движения тела (рис. 32,6).
Составляя уравнения равновесия (27), имеем:
В двух уравнениях имеются три неизвестные величины: Р, N и F. Для получения третьего уравнения по формуле (28) имеем > зависимость: 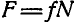
Выражая в уравнениях равновесия F через N, получим:
Оторда находим:
Задача №2
Определить наибольший и наименьший груз Р, при котором груз Q = 10 кГ не будет двигаться (рис» 33, а). Коэффициент трения груза Q о плоскость f=0,2.
Указание: при наименьшем грузе 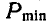
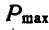
Составляя для каждого из случаев (рис. 33, б и 33, в) по два уравнения равновесия и принимая во внимание формулу (28), получим:
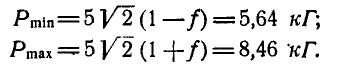
32
Законы Кулона
1. Сила трения скольжения находится в общей касательной плоскости соприкасающихся поверхностей тел и направлена в сторону, противоположную направлению возможного или реального скольжения тела под действием приложенных сил. Сила трения при покое зависит от активных сил и ее модуль заключен между нулем и максимальным значением, которое достигается в момент выхода тела из положения равновесия, т. е.
2. Максимальная сила трения скольжения при прочих равных условиях не зависит от площади соприкосновения трущихся поверхностей. Из этого закона следует, что для того, чтобы сдвинуть, например, кирпич, надо приложить одну и ту же силу независимо от того, какой гранью он положен на поверхность, широкой или узкой.
3. Максимальная сила трения скольжения пропорциональна нормальному давлению (нормальной реакции), т. е.
где безразмерный коэффициент 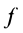
4. Коэффициент трения скольжения зависит от материала и физического состояния трущихся поверхностей, т. е. от величины и характера шероховатости, влажности, температуры и других условий. Коэффициент трения скольжения в зависимости от различных условий устанавливается экспериментально. Так, коэффициент трения для кирпича по бетону равен 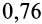
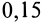
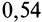
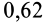
Опыты показывают, что при скольжении одного тела по поверхности другого с некоторой относительной скоростью возникает сила трения скольжения, равная максимальной, только при этом коэффициент трения скольжения незначительно изменяется в зависимости от скорости скольжения. Для большинства материалов он уменьшается с увеличением скорости скольжения, но для некоторых материалов, наоборот, увеличивается (трение кожи о металл).
В приближенных технических расчетах обычно считают, что коэффициент трения скольжения не зависит от относительной скорости скольжения.
В отличие от сухого трения трение при наличии смазывающего слоя между поверхностями определяется распределением относительной скорости скольжения в этом слое. В этом случае трение происходит не между поверхностями тел, а между слоями смазывающего вещества. Теория трения в смазывающем слое жидкости рассматривается в гидродинамике.
Угол и конус трения
Многие задачи на равновесие тела на шероховатой поверхности, т. е. при наличии силы трения, удобно решать геометрически. Для этой цели введем понятия угла и конуса трения.
Пусть твердое тело под действием активных сил находится на шероховатой поверхности в предельном состоянии равновесия, т. е. таком состоянии, когда сила трения достигает своего наибольшего значения при данном значении нормальной реакции (рис. 60). В этом случае полная реакция шероховатой поверхности 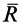
Этот наибольший угол 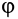
Угол трения 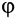
Но по третьему закону Кулона,
т. е. тангенс угла трения равен коэффициенту трения.
Рис. 60
Конусом трения называют конус, описанный полной реакцией, построенной на максимальной силе трения, вокруг направления нормальной реакции. Его можно получить изменяя активные силы так, чтобы тело на шероховатой поверхности находилось в предельных положениях равновесия, стремясь выйти из равновесия по всем возможным направлениям, лежащим в общей касательной плоскости соприкасающихся поверхностей.
Если коэффициент трения во всех направлениях одинаков, то конус трения круговой. Если не одинаков, то конус трения не круговой, например в случае, когда свойства соприкасающихся поверхностей различны (вследствие определенного направления волокон или в зависимости от направления обработки поверхности тел, если обработка происходит на строгальном станке и т. п.).
Равновесие тела на шероховатой поверхности
При равновесии сил, действующих на твердое тело, находящееся в равновесии на шероховатой поверхности, возникает дополнительно неизвестная сила реакции шероховатой поверхности— сила трения. В случае предельного равновесия сила трения достигает своего максимального значения и по формуле (1) выражается через нормальную реакцию. В общем случае равновесия сила трения находится между нулем и ее максимальным значением. Поэтому соответствующие условия равновесия, в которые входит сила трения после замены ее максимальным значением, становятся неравенствами. После этого неизвестные находят путем совместного решения уравнений и неравенств. Для всех неизвестных или для их части получают решения в виде неравенств.
Некоторые задачи на равновесие с учетом сил трения удобно решать геометрически с помощью конуса трения.
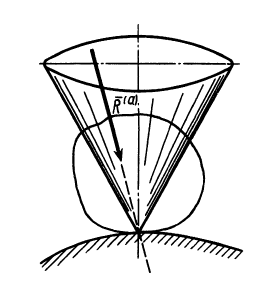
Можно сформулировать условия равновесия тела на шероховатой поверхности используя конус трения. Если активные силы, действующие на тело, приводятся к равнодействующей силе 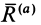
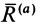
Очевидно, при изменении равнодействующей активных сил тело находится в равновесии до тех пор, пока составляющая 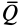
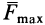
Рис. 61
Рис. 62
Предельным положением равновесия тела является случай, когда сила 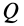
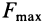
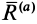
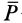
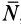
Тело нельзя вывести из равновесия любой по модулю активной силой, если ее линия действия проходит внутри конуса трения.
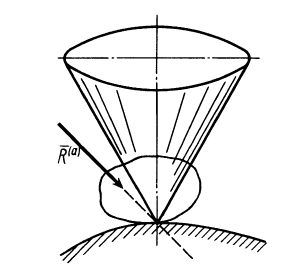
Если линия действия равнодействующей активных сил не проходит внутри конуса трения или по его образующей, то тело на шероховатой поверхности не может находиться в равновесии (рис. 63).
Рис. 63
Рис. 64
Пример 1.
Тело, сила тяжести которого 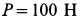
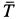
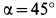
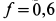
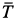
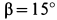
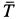
Решение. К телу приложены силы 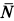
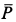
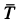
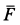
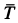
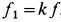
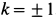
Составляем условия равновесия в виде суммы проекций сил на координатные оси для обоих предельных случаев. Имеем
По закону Кулона,
Решая эти уравнения относительно 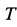
Отсюда при
при
Таким образом, сила 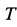
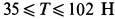
Пример 2.
Однородный тяжелый стержень 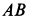
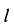
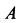
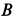
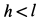
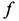
Рис. 65
Решение. Рассмотрим случай, когда точка 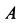
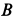
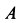
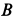
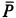
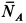
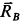
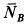
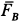
Составим условия равновесия плоской системы сил:
К этим условиям следует добавить неравенство для силы трения
Из уравнений равновесия находим
Из геометрических условий задачи имеем
Итак, для силы трения 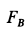
Исключая из них силу трения 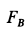
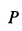
Искомое условие для коэффициента трения 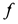
Видео:9 класс, 20 урок, Сила тренияСкачать

Трение качения
Если рассматриваемое тело имеет форму катка и под действием приложенных активных сил может катиться по поверхности другого тела, то из-за деформации поверхностей этих тел в месте соприкосновения могут возникнуть силы реакции, препятствующие не только скольжению, но и качению. Примерами таких катков являются различные колеса, как, например, у электровозов, вагонов, автомашин, шарики и ролики в шариковых и роликовых подшипниках и т. п.
Пусть цилиндрический каток находится на горизонтальной плоскости под действием активных сил. Соприкосновение катка с плоскостью из-за деформации фактически происходит не вдоль одной образующей, как в случае абсолютно твердых тел, а по некоторой площадке. Если активные силы приложены симметрично относительно среднего сечения катка, т. е. вызывают одинаковые деформации вдоль всей его образующей, то можно изучать только одно среднее сечение катка. Этот случай рассмотрен ниже.
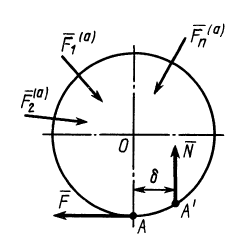
Активные силы, действующие на катки в виде колес (рис. 66), кроме силы тяжести 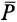
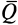
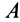
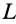
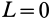
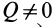
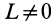
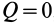
Если активные силы, действующие на колесо, привести к точке 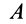
Рис. 66
Рис. 67
Рис. 68
Соприкосновение среднего сечения колеса с неподвижной плоскостью из-за деформации колеса и плоскости происходит по некоторой линии 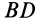
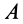
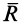
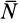
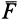
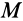
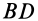
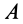
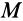
Приведем активные силы 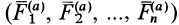
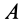
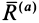
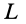
При равновесии катка, т. е. когда каток не катится и не скользит по плоскости, активные силы уравновешиваются силами реакций связи и, следовательно,
Изменив активные силы, приложенные к катку так, чтобы увеличивался момент 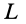
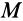
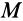
Установлены следующие приближенные законы для наибольшего момента пары сил, препятствующей качению:
1. Наибольший момент пары сил, препятствующей качению, в довольно широких пределах не зависит от радиуса катка.
2. Предельное значение момента 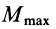
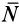
Коэффициент пропорциональности 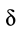
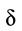
3. Коэффициент трения качения 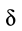
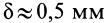
Законы трения качения, как и законы трения скольжения, справедливы для не очень больших нормальных давлений и не слишком легко деформирующихся материалов катка и плоскости.
Эти законы позволяют не рассматривать деформации катка и плоскости, считая их абсолютно твердыми телами, касающимися в одной точке. В этой точке соприкосновения в среднем сечении катка кроме нормальной реакции и силы трения надо приложить еще и пару сил, препятствующую качению.
Коэффициент трения качения равен длине 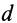
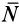
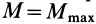
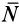
В предельном случае равновесия катка 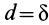
Для того чтобы каток не скользил, необходимо выполнение условия
Для заданных активных сил соответственно
Для того чтобы каток не катился, должно выполняться условие
Для активных сил оно имеет вид
Рис. 69
Рис. 70
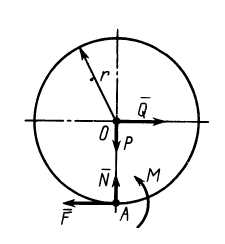
Для примера рассмотрим случай ведомого колеса, к которому кроме силы тяжести 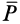
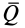
Если каток находится в равновесии, то из условий равновесия плоской системы сил, приложенных к катку, получаем
где за моментную точку взята точка 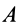
В случае отсутствия скольжения по формуле (4) с учетом условий равновесия
Аналогично, при отсутствии качения по формуле (5) имеем
Таким образом, при отсутствии скольжения сила 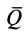
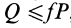
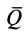
Если 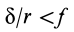
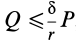
Если 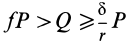
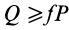
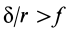
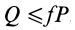
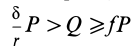
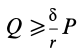
В том случае, если 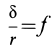
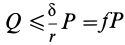
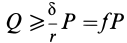
Обычно 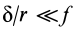
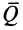
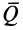
С точки зрения затраты энергии выгодно заменять скольжение качением. Этим объясняется преимущество шариковых и роликовых подшипников по сравнению с подшипниками скольжения, если даже в них трение и не уменьшается введением смазывающего вещества.
Аналогично трению качения можно рассмотреть и явление возникновения так называемого трения верчения, т.е. случая, когда активные силы стремятся вращать тело, например в форме шара, вокруг нормали к общей касательной поверхности соприкосновения.
В этом случае возникает пара сил, препятствующая верчению, причем наибольший ее момент, возникающий в момент начала верчения, также прямо пропорционален нормальной реакции. Коэффициент пропорциональности, т. е. коэффициент трения верчения, обычно значительно меньше коэффициента трения качения.
Равновесие с учетом сил трения
Задачи, приведенные в этом параграфе, отличаются от предыдущих тем, что в них рассматривается равновесие тел, имеющих, кроме идеальных, еще и реальные связи, т. е. связи с трением.
При свободном опирании тела на поверхность идеальной связи реакция такой связи 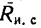
Если же тело опирается на поверхность реальной связи (в отличие от идеальных связей реальные связи условимся отмечать двойной штриховкой), то ее реакция 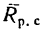
Поясним это общее положение следующим примером.
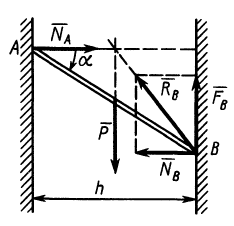
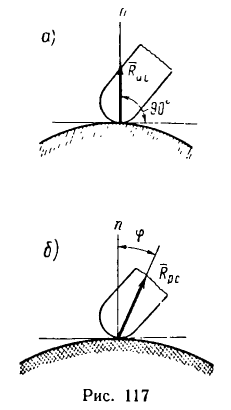
Наклонный брус (рис. 118, а), вес которого G, опирается в двух
точках А и В соответственно на вертикальную и горизонтальную поверхности идеальных связей. Этот брус не может находиться в равновесии, потому что три силы —вес бруса G и реакции 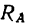
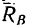
Чтобы брус, показанный на рис. 118, а, находился в равновесии, необходимо наложить еще одну связь, например, удержать брус шнуром или упереть в выступ на горизонтальной плоскости (обе возможные связи показаны пунктиром).
Теперь представим, что в точке В брус опирается не на идеально гладкую, а на шероховатую (реальную) поверхность (рис 118, б). В этом случае брус может находиться в равновесии без дополнительной связи (шнура или упорной планки). Значит три силы — вес 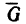
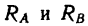
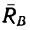
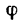
Если реакцию 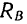
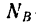
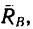
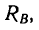
При увеличении угла а, характеризующего наклон бруса относительно горизонтальной поверхности, угол 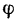
Если же уменьшать угол а, то угол ф, характеризующий отклонение реакции 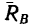
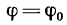
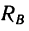
У гол 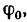
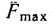
Для случая предельного равновесия между силой трения и углом трения имеем такую зависимость; 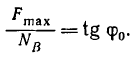
Постоянное для данной пары соприкасающихся тел значение 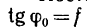
При решении задач необходимо учитывать, что сила трения направлена всегда в сторону, противоположную той, при которой точка может скользить по идеальной поверхности.
Если в число реакций связей, обеспечивающих равновесие тела, входит сила трения, то такое состояние равновесия называется самоторможением. Во всех приведенных ниже задачах рассмотрены различные случаи самоторможения (равновесия при наличии силы трения) и условия, при которых возможно самоторможение.
Задача №3
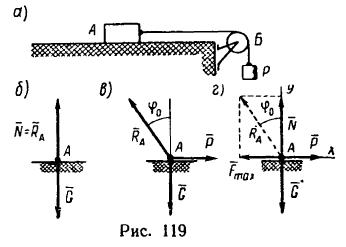
Тело А массой 8 кг поставлено на шероховатую горизонтальную поверхность стола. К телу привязана нить, перекинутая через блок Б (рис. 119, а). Какой груз Р можно подвязать к концу нити, свешивающейся с блока, чтобы не нарушить равновесия тела А? Коэффициент трения f = 0,4. Трением на блоке пренебречь.
1. Если масса тела А m = 8 кг, то его вес
2. Пренебрегая размерами тела, будем считать, что все силы приложены к точке А.
3. Когда тело поставлено на горизонтальную поверхность, то на него действуют только две силы: вес 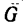
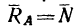
4. Если же приложить некоторую силу 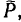
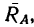
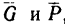
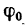
5. Разложив реакцию 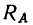
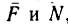
Спроектировав эту систему сил на оси хну, получим два уравнения равновесия:
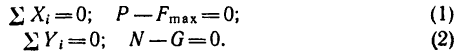
Решаем полученную систему уравнений: 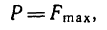
но 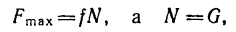
поэтому
Таким образом, равновесие тела А сохраняется при условии, что к концу нити, перекинутой через блок, подвешен груз, не превышающий по весу 31,4 н.
При этом масса груза Р
Задача №4
При каком минимальном коэффициенте трения между полом и лестницей последняя может находиться в равновесии, опираясь верхним концом о гладкую стену, как показано на рис. 120, а? Вес лестницы G = 120 н.
1. На лестницу действует только одна нагрузка — ее собственный вес, приложенный в точке С посредине длины лестницы АВ.
2. Вес лестницы уравновешен реакцией 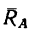
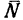
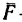
3. Составим три уравнения равновесия:
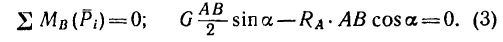
4. Из уравнений (1) и (3) 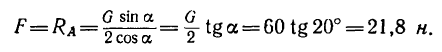
А так как N = G [из уравнения (2)[, то минимальный коэффициент трения, обеспечивающий равновесие лестницы. 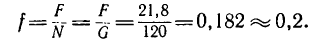
Таким образом, при 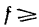
Задача №5
В месте соприкосновения пола и лестницы в предыдущей задаче коэффициент трения f= 0,4. Сможет ли человек, масса которого 70 кг, подняться по лестнице до самого верха и чтобы лестница при этом не скользила по полу?
1. К силам 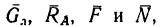
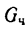
2. Вес человека
3. Человек сможет подняться до самого верха лестницы лишь в том случае, если горизонтальная составляющая реакции пола (сила 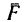
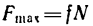
4. Составим уравнения равновесия:
5. Из уравнения (2)
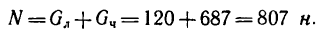
Максимальная сила трения, которая может возникнуть в данном случае
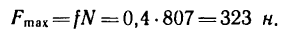
Из уравнений (1) и (3) находим силу F—горизонтальную составляющую реакции пола, которая может обеспечить равновесие лестницы с человеком, стоящим наверху:
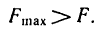
Следовательно, человек сможет подняться по лестнице до самого верха.
Задача №6
При каких значениях угла а, образуемого с гладкой вертикальной стеной, лестница, опирающаяся нижним концом о шероховатый горизонтальный пол, будет находиться в равновесии, если, кроме собственного веса, она ничем не нагружена и известно, что коэффициент трения при соприкосновении лестницы с полом f?
1. Для решения этой задачи воспользуемся рис. 120, б, так как на лестницу действуют те же четыре силы: вес лестницы 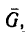
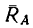
2. Лестница не выйдет из состояния равновесия (не начнет скользить) до тех пор, пока
т. е. пока горизонтальная составляющая реакции пола остается меньше максимальной силы трения, возникающей при опирании лестницы о пол в данном случае.
3. Из уравнений (1) и (3), составленных при решении задачи 90-15, найдено, что
Сопоставляем уравнения (а) и (б):
А так как в данном случае G =N, то лестница находится равновесии до тех пор, пока выполняется неравенство
или
где 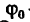
Следовательно, лестница находится в равновесии до тех пор, пока тангенс угла, образуемого лестницей с вертикальной гладкой стеной, остается меньше удвоенного коэффициента трения между лестницей и полом. Например, при f=0,4
и неравенство (в) соблюдается при значениях углов
Следовательно, при f=0,4 лестница не будет скользить по полу при любом значении угла a от 0 до 38°40′.
Следующую задачу рекомендуется решить самостоятельно.
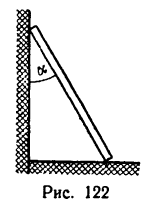
Задача №7
При каких значениях угла a однородная лестница, опирающаяся на шероховатые стену и пол (рис. 122), будет находиться в равновесии? Коэффициенты трения при опирании лестницы о стену и о пол считать одинаковыми и равными f.
Ответ.
Указание. В данной задаче в системе сил, действующих на лестницу, образуется пять неизвестных: четыре реакции и угол а. Поэтому при решении задачи нужно к трем уравнениям равновесия добавить еще два уравнения, выражающих зависимость сил трения от нормального давления.
Задача №8
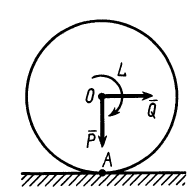
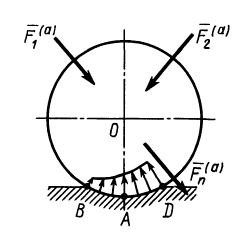
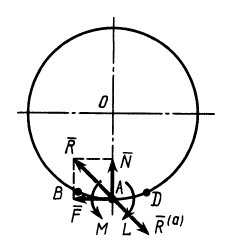
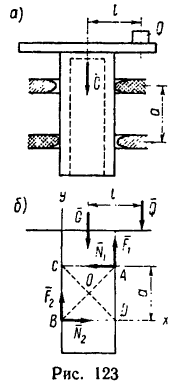
Цилиндр с горизонтальной площадкой наверху (рис. 123, а), находясь в двух кольцевых направляющих, скользит вниз, так как между поверхностью цилиндра и поверхностями направляющих имеется незначительный зазор. Вес цилиндра 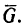
1. На цилиндр в состоянии равновесия действуют две нагрузки: вес 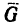
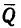
2. Груз Q, помещенный на горизонтальную площадку, прижимает цилиндр к верхнему направляющему кольцу в точке А, а к нижнему — в точке В. Благодаря зазору в точках С и D цилиндр не касается направляющих колец. В точках А и В возникают две реакции, которые заменим их составляющими 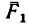
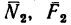
3. Образовалось пять неизвестных величин:
Если спроектировать все силы на ось х, то получим
также, имея в виду равенство (1а), находим что
Скоректировав все силы на ось у, получим четвертое уравнение:
откуда с учетом (За)
Приняв за центр моментов точку О, лежащую на оси цилиндра и на середине расстояния а, составим пятое уравнение — уравнение моментов, в котором d- диаметр цилиндра (d = CA = BD): 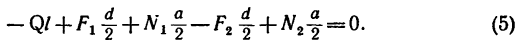
Имея в виду равенства (1а) и (За), уравнение (5) можно упростить так:
Если теперь в уравнение (2) подставить значение 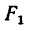
И теперь выражение (5а) принимает окончательный вид:
При значениях /, удовлетворяющих полученному неравенству, цилиндр не скользит вниз.
Задача №9
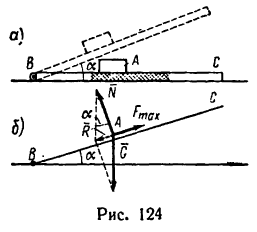
Тело А поставлено на негладкую пластину ВС, которую можно поворачивать около шарнира В. Коэффициент трения f между телом А и пластиной ВС известен. Определить, при каких значениях угла а (рис. 124, а) тело А будет оставаться на пластине в покое? Решение.
1. Представим, что пластина ВС наклонена к горизонту на некоторый угол а (рис. 124, б).
При этом положении пластины на тело А действуют три силы: его собственный вес 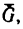
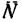
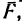
2. Тело А будет находиться в покое до тех пор, пока равнодействующая сил 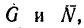
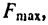
но
поэтому
или 
Следовательно, пока тангенс угла наклона пластины к горизонту меньше коэффициента трения, тело А остается в покое.
Это положение выражает так называемое условие самоторможения тела по наклонной плоскости.
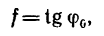
где 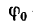
Так как углы 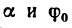
Тело А находится в покое на наклонной плоскости до тех пор, пока угол наклона плоскости меньше угла трения.
Следующую задачу рекомендуется решить самостоятельно.
Равновесие при наличии трения
Постановка Задачи. Конструкция состоит из двух шарнирно соединенных между собой тел. Одна из опор конструкции представляет собой одностороннюю связь и допускает проскальзывание с трением. Коэффициент трения, размеры конструкции и часть внешних нагрузок заданы. Найти пределы изменения одной из внешних нагрузок, действующей на конструкцию в условии равновесия.
1. Задаем направление возможного движения подвижной опоры, скользящей с трением. Прикладываем к этой опоре силу трения, направляя ее в сторону противоположную возможному движению. Предельное значение силы трения связываем с величиной нормальной реакции опоры N по формуле Кулона 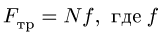
2. Решаем задачу о равновесии системы тел. Для этого разбиваем систему на две отдельные части, для которых составляем и решаем уравнения равновесия. Из решения определяем предельное значение нагрузки д.чя заданного направления скольжения опоры.
3. Меняем направление возможного движения системы и направление предельной силы трения. Предыдущий пункт плана выполняем заново и определяем другое предельное значение нагрузки. Два найденных значения нагрузки определяют ту область ее изменения, при которой конструкция находится в равновесии.
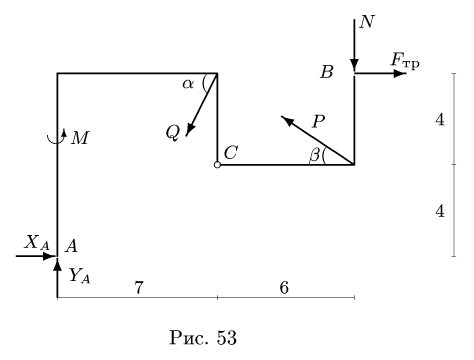
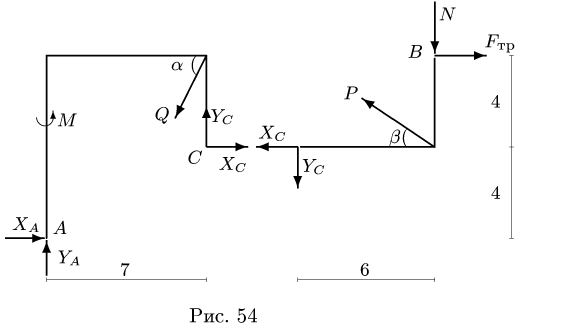
Задача №10
Конструкция состоит из двух частей, шарнирно соединенных в точке С (рис. 52). Опора В представляет собой одностороннюю связь и допускает проскальзывание с коэффициентом трения 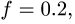
Размеры даны в метрах. Найти продолы изменения нагрузки Р, действующей под углом 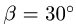
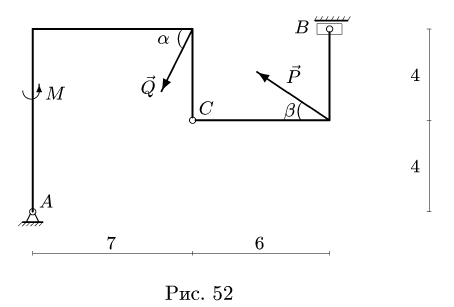
Решение
1. Задаем направление возможного движения подвижной опоры, скользящей с трением Предполагая возможное движение ползуна В влево, силу трения 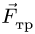
где 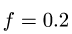
2. Решаем задачу о равновесии системы тел. Для этого систему разбиваем по шарниру С на две отдельные части — АС и СВ. Реакции шарнира С 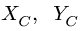
Действие ползуна заменяем нормальной реакцией N, направленной вниз, так как ползун по условию задачи является односторонней связью, и силой трения 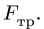
Уравнения (2) вместе с законом Кулона (1) образуют замкнутую систему трех линейных уравнений с тремя неизвестными 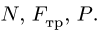
При 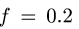
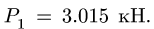
3. Меняем направление возможного движения системы и направление предельной силы трения. Пусть ползун В движется вправо. Силу 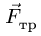
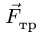
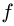
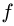
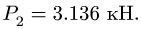
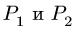
Чтобы убедиться, что равновесие соответствует значениям нагрузки между этими числами, определим Р при 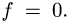
Из выражения (3) для N также следует, что при 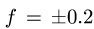
Этим нагрузкам соответствуют следующие значения нормальной реакции:
Замечание. Неравенство 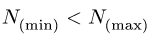
Трение качения
Постановка задачи. Система состоит из двух цилиндров, соединенных стержнем. Цилиндры могут кататься без проскальзывания, один цилиндр без сопротивления, другой — с трением качения. В каких пределах меняется внешний момент, приложенный к одному из цилиндров, в условии равновесия системы?
Трение качения происходит за счет деформации цилиндра и опорной поверхности в месте контакта. В результате реакция опоры смещается в сторону возможного движения на половину длины площадки контакта и создает момент сопротивления. Плечо этого момента принимают за коэффициент трения качения. Таким образом, 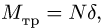
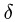
в теле мала, а глубиной продавливания цилиндра в поверхность (или величиной смятия цилиндра) пренебрегают. Коэффициент трения качения зависит не только от свойств материала цилиндра и поверхности, но и от радиуса цилиндра.
1. Задаем направление возможного движения при достижении условия предельного равновесия. К катящемуся телу (цилиндру, колесу) прикладываем момент трения качения, направляя его в сторону, противоположную возможному движению. Не забываем про силу сцепления в точке контакта, направленную вдоль плоскости.
2. Решаем задачу о равновесии системы тел. Используем метод разбиения системы на отдельные тела. Внешние и внутренние связи заменяем их реакциями. Составляем и решаем уравнения равновесия. Оси координат для уравнения проекций для цилиндрических тел выбираем вдоль нормальной реакции, а уравнение моментов составляем относительно точки касания. Из решения системы уравнений равновесия определяем условие предельного равновесия.
3. Меняем направление возможного движения системы и направление момента трения качения. Решаем задачу заново, определяем второе условие предельного равновесия.
Задача №11
Система состоит из двух цилиндров весом 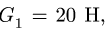
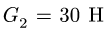
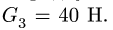
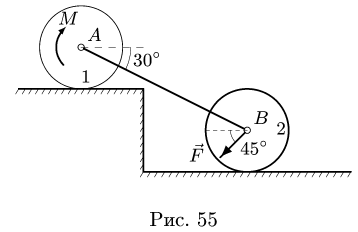
Коэффициент трения качения 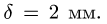
1. Задаем направление возможного движения при достижении условия предельного равновесия. Пусть за счет достаточно большой, по сравнению с моментом М, силы F произойдет движение системы влево. Тогда момент трения качения, приложенный к цилиндру 2, будет направлен по часовой стрелке (рис. 57). Его величину находим по формуле
2. Решаем задачу о равновесии системы двух цилиндров и стержня. Разбиваем систему на три тела (рис. 56, 57, 58). Внешние связи заменяем реакциями 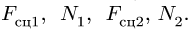
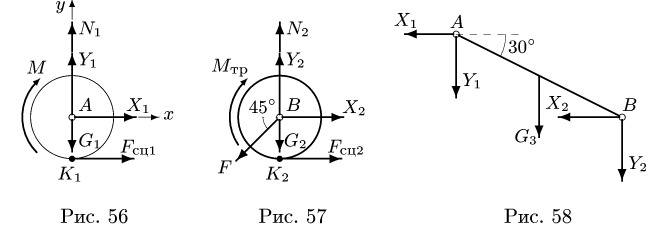
Реакции 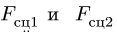
При составлении системы семи уравнений с неизвестными 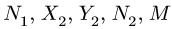
Составляем уравнения равновесия для цилиндра 1 (рис. 56):
Уравнения равновесия цилиндра 2 (рис. 57) имеют вид
Уравнения равновесия стержня АВ (рис. 58) имеют вид
Из решения системы уравнений (1-3) определяем
Радиус и коэффициент трения качения переводим в метры R = 0.5 м, 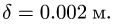
Убеждаемся, что 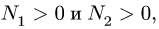
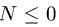
3. Меняем направление возможного движения системы. Пусть за счет действия момента М произойдет движение системы вправо. Момент трения качения направим против часовой стрелки (рис. 59). Составляя уравнения равновесия для новой системы сил, заметим, что отличие от прежней системы проявляется только в знаке 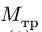
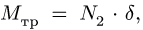
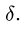
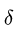
Точно так же находим нормальные реакции опор: 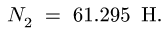
цилиндру 1, изменяется в пределах (в Нм)
| Рекомендую подробно изучить предмет: |
|
| Ещё лекции с примерами решения и объяснением: |
- Пространственная система сил
- Центр тяжести
- Кинематика точки
- Плоское движение твердого тела
- Теория пар сил
- Приведение системы сил к простейшей системе
- Условия равновесия системы сил
- Плоская система сил
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Сравнение сил трения, скольжения и каченияСкачать

Сила трения
теория по физике 🧲 динамика
Трение — вариант взаимодействия двух тел. Оно возникает при движении одного тела по поверхности другого. При этом тела действуют друг на друга с силой, которая называется силой трения. Сила трения имеет электромагнитную природу.
Сила трения — сила, возникающая между телами при их движении или при попытке их сдвинуть. Обозначается как F тр. Единица измерения — Н (Ньютон).
Трение бывает сухим и жидким. В школьном курсе физике изучается сухое трение.
Виды сухого трения:
- трение скольжения;
- трение качения;
- трение покоя.
Видео:Сила трения скольжения. 9 класс. Решение задачСкачать

Трение скольжения
Трение скольжения — трение, возникающее при скольжении одного тела по поверхности другого. Сила трения скольжения направлена противоположно направлению движения тела: F тр↑↓ v .
Сила трения скольжения определяется формулой:
μ — коэффициент трения, N — сила реакции опоры, Fдавл. — сила нормального давления
Сила реакции опоры и сила нормального давления — равные по модулю, но противоположные по направлению силы. Если тело не перемещается с ускорением относительно оси ОУ, модули силы реакции опоры и силы нормального давления равны модулю силы тяжести, действующей на это тело.
Силу трения скольжения зависит от степени неровности (шероховатости) поверхности. Поэтому ее можно легко менять.
Чтобы увеличить силу трения скольжения, нужно сделать поверхность тела более шероховатой. Так, чтобы зимой автомобили не скользили по голому льду, автомобилисты используют зимние шины. От летних они отличаются глубоким протектором и наличием шипов, создающих дополнительную неровность.
Чтобы уменьшить силу трения скольжения, нужно сделать поверхность более ровной. Ее можно отшлифовать или смазать. Так, чтобы лыжи скользили по снегу лучше, их смазывают специальными мазями или парафинами.
Пример №1. Конькобежец массой 70 кг скользит по льду. Какова сила трения, действующая на конькобежца, если коэффициент трения скольжения коньков по льду равен 0,002?
Сила реакции опоры по модулю равна силе тяжести, действующей на конькобежца. Отсюда:
Видео:ДВИЖЕНИЕ ПО НАКЛОННОЙ ПЛОСКОСТИ | механика 10 классСкачать

Видео:Статика. Трение скольжения. Лекция (28)Скачать

Трение покоя
Трение покоя возникает при попытке сдвинуть предмет с места. Трение покоя противоположно направлено приложенной к телу силе (в сторону возможного движения).
Сила трения покоя всегда больше нуля, но всегда меньше силы трения скольжения:
Способы определения вида силы трения, возникающей между телами, и ее модуля:
- Когда к телу прикладывается сила F , модуль которой меньше силы трения скольжения, возникает сила трения покоя. Тело продолжает покоиться. При этом модуль силы трения покоя равен модулю прикладываемой к телу силы. Если F
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
Сила, приложенная к ящику, меньше силы трения скольжения. Значит, между ящиком и полом возникает сила трения покоя. Модуль силы трения покоя равен модулю приложенной силы:
Видео:Наклонная плоскость. Расстановка сил | 50 уроков физики (6/50)Скачать

Описание движения тел с учетом сил трения
Движение тела по горизонтальной плоскости
Равноускоренное движение по горизонтали, сила тяги параллельная плоскости
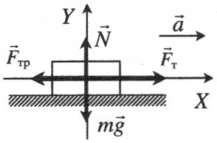
Проекция на ось ОХ:
Проекция на ось ОУ:
Равнозамедленное движение по горизонтали, сила тяги параллельная плоскости
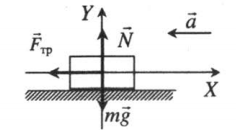
Проекция на ось ОХ:
Проекция на ось ОУ:
Ускоренное движение по горизонтали, сила тяги направлена под углом к горизонту (вверх)
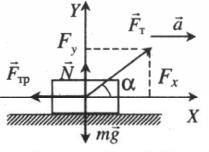
Проекция на ось ОХ:
Проекция на ось ОУ:
Ускоренное движение по горизонтали, сила тяги направлена под углом к горизонту (вниз)
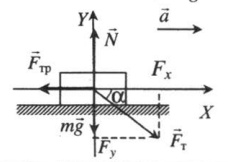
Проекция на ось ОХ:
Проекция на ось ОУ:
Внимание! В случаях, когда сила тяги F т направлена под углом к плоскости движения, сила реакции опоры не равна силе тяжести: N ≠ mg.
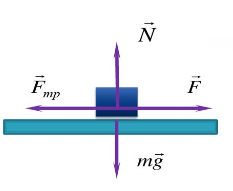
Пример №3. Брусок массой 1 кг движется равноускоренно по горизонтальной поверхности под действием силы 10 Н, как показано на рисунке. Коэффициент трения скольжения равен 0,4, а угол наклона α — 30 градусов. Чему равен модуль силы трения? 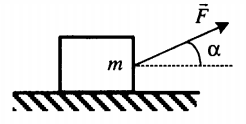
Проекция сил на ось ОУ выглядит так:
Отсюда силы реакции опоры равна:
Подставим ее в формулу для вычисления силы трения и получим:
Движение тела по вертикальной плоскости
Тело прижали к вертикальной плоскости и удерживают
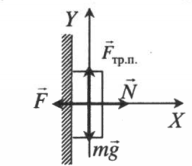
Проекция на ось ОХ:
Проекция на ось ОУ:
Тело поднимается под действием силы тяги, направленной под углом к вертикали
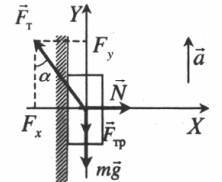
Проекция на ось ОХ:
Проекция на ось ОУ:
Пример №4. Груз массой 50 кг удерживают на вертикальной плоскости, коэффициент трения которой равен 0,4. Определить, какую силу нужно приложить, чтобы груз оставался в состоянии покоя. Проекция на ось ОХ:
Отсюда следует, что сила должна быть равна силе реакции опоры. Проекция на ось ОУ:
Перепишем, выразив силу трения через силу реакции опоры:
Отсюда выразим силу реакции опоры: 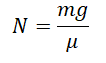
Движение тела по наклонной плоскости
Движение вниз без трения
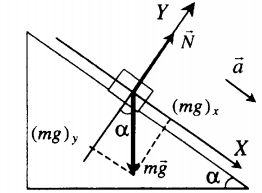
Тело покоится на наклонной плоскости
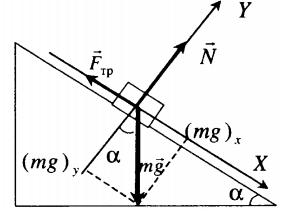
Тело удерживают на наклонной плоскости
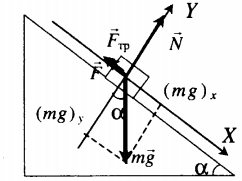
m g + N + F + F тр = m a
Равноускоренное движение вверх с учетом силы трения
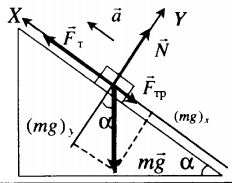
Равномерное движение вверх с учетом силы трения
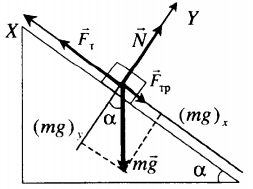
m g + N + F + F тр = m a
Пример №5. Брусок массой 200 г покоится на наклонной плоскости. Коэффициент трения между поверхностью бруска и плоскостью равен 0,6. Определите величину силы трения, если угол наклона плоскости к горизонту равен 30 градусам. 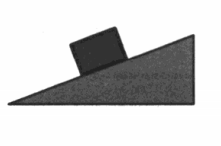
Отсюда сила трения равна:
Подставляем известные данные и вычисляем:
Полезная информация
| Косинус угла наклона | 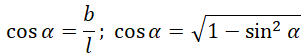 |
| Синус угла наклона (уклон) | 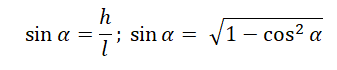 |
| Тангенс угла наклона | 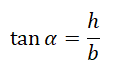 |
При исследовании зависимости силы трения скольжения F тр от силы нормального давления F д были получены следующие данные:
📹 Видео
Коэффициент тренияСкачать

Трение скольженияСкачать

СИЛА ТРЕНИЯ | коэффициент трения | ДИНАМИКАСкачать

Трение каченияСкачать

Сила трения. Трение покоя | Физика 7 класс #23 | ИнфоурокСкачать

Сила трения покоя и скольжения | ФизикаСкачать

Силы трения. 7 класс.Скачать

Силы трения. Практическая часть - решение задачи. 7 класс.Скачать

Урок 87. Движение по наклонной плоскости (ч.1)Скачать

Лабораторная работа «Измерение коэффициента трения скольжения»Скачать

Физика 10 класс (Урок№10 - Силы трения.)Скачать