Содержание:
Прямолинейное неравномерное движение, ускорение:
На практике прямолинейное равномерное движение наблюдается очень редко. Скорость движущегося автомобиля, поезда, самолета, частей механизма и т.д. может изменяться и по величине, и по направлению.
Прямолинейное движение, при котором за равные промежутки времени материальная точка совершает разные перемещения, называют прямолинейным неравномерным движением.
При таком движении числовое значение скорости не остается неизменным, поэтому для описания неравномерного движения пользуются понятиями средней и мгновенной скорости.
Видео:Прямолинейное равномерное и неравномерное движение. 7 класс.Скачать

Средняя скорость
Средняя скорость неравномерно движущейся материальной точки на данном участке траектории равна отношению ее перемещения на этом участке ко времени совершения этого перемещения:
Средняя путевая скорость материальной точки при неравномерном движении равна отношению всего пройденного пути ко времени, затраченному на прохождение этого пути:
Средняя скорость материальной точки, движущейся со скоростями 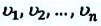
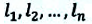
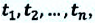
Если 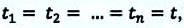
Видео:Урок 12. Равномерное прямолинейное движениеСкачать

Мгновенная скорость.
Скорость материальной точки в данный момент времени или в данной точке траектории называют мгновенной скоростью.
Мгновенная скорость в некоторой точке является векторной величиной и определяется как предел отношения достаточно малого перемещения 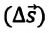
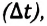
Где 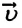
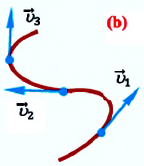
С течением времени мгновенная скорость может увеличиваться, уменьшаться и изменять направление. Направление мгновенной скорости в данной точке траектории совпадает с направлением касательной к траектории в этой точке (b). Проекция вектора мгновенной скорости в прямоугольной системе координат равна первой производной координаты по времени:
Видео:Уравнение равномерного прямолинейного движения | Физика 10 класс #3 | ИнфоурокСкачать

Ускорение
Быстрота изменения мгновенной скорости при неравномерном движении по величине и направлению характеризуется векторной физической величиной, называемой ускорением:
Ускорение — это физическая величина, равная отношению изменения скорости ко времени, за которое это изменение произошло:
Если измерение времени начинается с нуля 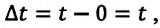
Направление ускорения совпадает с направлением вектора
Для простоты здесь и в последующем будет рассматриваться такое неравномерное прямолинейное движение материальной точки, при котором за любые равные промежутки времени происходит одинаковое изменение скорости. Такое движение называется равнопеременным движением.
Видео:Равномерное и неравномерное движениеСкачать

Равнопеременное движение
Равнопеременное движение — это движение, при котором за любые равные промежутки времени происходит одинаковое изменение скорости. При равнопеременном движении значение и направление ускорения не меняются:
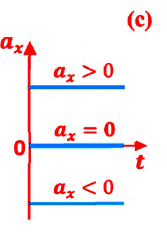
При равнопеременном движении проекция ускорения на любую ось, например ось 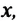
Это значит, что при равнопеременном движении график зависимости ускорения от времени представляет собой прямую линию, параллельную оси времени, — проекция ускорения на выбранную ось от времени не зависит (с).
В СИ за единицу ускорения принят 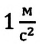
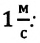
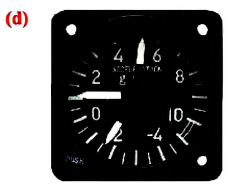
Знаете ли вы? Ускорение—одна из наиболее значимых величин, используемых в физике и технике. Известно, что при постепенном торможении автомобиля, автобуса и поезда пассажиры не чувствуют дискомфорта, однако при резком торможении для них возникает серьезная опасность. Значит, важно не просто изменение скорости, а быстрота изменения скорости. Для контроля за изменением скорости машин и механизмов используется прибор, измеряющий ускорение — акселерометр (лат.: accelero — «ускоряю » и греч.: metreo — «измеряю «) (d).
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Прямолинейное равноускоренное движение
- Сложение скоростей
- Ускорение в физике
- Скорость при равнопеременном движении
- Скалярные и векторные величины и действия над ними
- Проекция вектора на ось
- Путь и перемещение
- Равномерное прямолинейное движение
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Равномерное прямолинейное движение - физика 9Скачать

Неравномерное прямолинейное движение

Средняя оценка: 4.5
Всего получено оценок: 121.
Средняя оценка: 4.5
Всего получено оценок: 121.
Наиболее простым видом движения является равномерное прямолинейное движение. Рассмотрим более сложный случай – неравномерное прямолинейное движение.
Видео:МЕХАНИЧЕСКОЕ ДВИЖЕНИЕ: Равномерное движение и Прямолинейное Движение || Скорость — Физика 7 классСкачать

Неравномерное движение тела
При равномерном движении тело за равные промежутки времени проходит одинаковый путь. Однако в Природе такое движение встречается достаточно редко. В большинстве случаев за одинаковые интервалы времени тела проходят различный путь. Такое движение называется неравномерным.

Видео:Прямолинейное равноускоренное движение. Ускорение | Физика 9 класс #5 | ИнфоурокСкачать

Скорость при неравномерном движении
Если для прямолинейного равномерного движения скорость в любой точке траектории равна отношению пройденного пути ко времени его прохождения, то для неравномерного движения это не так. Скорость при неравномерном прямолинейном движении может меняться. Поэтому для такого движения поступают иначе. Используются два варианта.
Средняя скорость
Во-первых, мы можем пренебречь изменением скорости во время прохождения пути, и считать, что скорость все время была одной и той же. Такая скорость называется средней.
Для определения средней скорости необходимо найти отношение всего пути к полному времени его прохождения.
Формула средней скорости:

Допустим, автомобиль проехал первые 50 км за час, потом полтора часа стоял, а за следующие полчаса проехал 40км. Путь его состоял из двух участков. Для нахождения средней скорости найдем отношение полного значения пути к полному значению времени:
Мгновенная скорость
Среднюю скорость удобно использовать там, где внимание уделяется общему результату движения. Однако, если необходимо описание движения тела в пути, среднюю скорость использовать нельзя. В самом деле, в приведенном примере автомобиль ни разу не двигался со средней скоростью.
Можно поступить иначе. Не пренебрегать изменениями скорости в пути, а поделить путь на небольшие промежутки, и считать скорость постоянной на каждом. Для приведенного выше примера можно взять три промежутка – час, полтора часа и полчаса. Вычислив скорости на них, мы получим значения 50 км/ч, 0 км/ч, 80 км/ч.
В реальном неравномерном движении изменение скорости происходит не скачками, а плавно. Поэтому для точного описания такого движения берут как можно больше промежутков, время прохождения каждого из которых стремится к нулю.
Отношения длины малого промежутка $ΔS$ ко времени его прохождения $Δt$ дает значение, называемого мгновенной скоростью.
Формула мгновенной скорости:
$$v_= <ΔSover >, при ΔS rightarrow 0,Δtrightarrow 0$$
В высшей математике доказывается, что, несмотря на то, что и $ΔS$, и $Δt$ стремятся к нулю, их отношение (мгновенная скорость) имеет вполне реальное значение.
Мгновенная скорость – величина векторная, ее направление совпадает с направлением перемещения.

Видео:Равномерное и неравномерное движение | Физика 7 класс #10 | ИнфоурокСкачать

Что мы узнали?
Для описания неравномерного прямолинейного движения используются понятия средней и мгновенной скорости. Средняя скорость используется чаще там, где важен общий результат движения, мгновенная скорость – там, где важны мелкие изменения движения.
Видео:Прямолинейное движение. 10 класс.Скачать

Уравнение движения неравномерного прямолинейного движения
При неравномерном движении тело может за равные промежутки времени проходить как равные, так и разные пути.
Для описания неравномерного движения вводится понятие средней скорости .
|
Средняя скорость, по данному определению, величина скалярная потому, что путь и время величины скалярные.
Однако среднюю скорость можно определять и через перемещение согласно уравнению
В этом случае среднюю скорость следует считать величиной векторной потому, что она определяется через отношение векторной величины к скалярной.
Средняя скорость прохождения пути и средняя скорость перемещения – это две разные величины, которые могут характеризовать одно и то же движение.
При расчете средней скорости очень часто допускается ошибка, состоящая в том, что понятие средней скорости подменяется понятием среднего арифметического скоростей тела на разных участках движения. Чтобы показать неправомерность такой подмены рассмотрим задачу и проанализируем ее решение.
Из пункта в пункт выходит поезд. Половину всего пути поезд движется со скоростью 30 км/ч, а вторую половину пути – со скоростью 50 км/ч.
Чему равна средняя скорость движения поезда на участке ?
Движение поезда на участке и на участке равномерное. Взглянув на текст задачи, нередко сразу хочется дать ответ: υср = 40 км/ч.
Да потому, что нам кажется, что для вычисления средней скорости вполне подходит формула, используемая для расчета среднего арифметического.
Давайте разберемся: можно ли использовать эту формулу и рассчитывать среднюю скорость путем нахождения полусуммы заданных скоростей.
Для этого рассмотрим несколько иную ситуацию.
Допустим, мы правы и средняя скорость действительно равна 40 км/ч.
Тогда решим другую задачу.
Из пункта в пункт выходит поезд. Половину всего времени (до точки ) он движется со скоростью 30 км/ч, а вторую половину времени – со скоростью 50 км/ч.
Чему равна средняя скорость поезда на участке ?
Как видно, тексты задач очень похожи, есть только «очень маленькая» разница.
Если в первом случае речь идет о половине пути, то во втором случае речь идет о половине времени.
Очевидно, что точка во втором случае находится несколько ближе к точке , чем в первом случае, и ожидать одинаковых ответов в первой и второй задаче, вероятно, нельзя.
Если мы, решая вторую задачу, так же дадим ответ, что средняя скорость равна полусумме скоростей на первом и втором участке, мы не можем быть уверены, что мы решили задачу правильно. Как быть?
Выход из положения следующий: дело в том, что средняя скорость не определяется через среднее арифметическое . Есть определяющее уравнение для средней скорости, согласно которому для нахождения средней скорости на некотором участке, надо весь путь, пройденный телом, поделить на все время движения:
Начинать решение задачи нужно именно с формулы, определяющей среднюю скорость, даже если нам кажется, что мы в каком-то случае можем использовать более простую формулу.
Будем двигаться от вопроса к известным величинам.
Неизвестную величину υср выражаем через другие величины – 0 и Δ0.
Оказывается, что обе эти величины неизвестны, поэтому мы должны выразить их через другие величины. Например, в первом случае: 0 = 2 ∙ , а Δ0 = Δ1 + Δ2.
Подставим эти величины, соответственно, в числитель и знаменатель исходного уравнения.
Во втором случае мы поступаем точно так же. Нам не известен весь путь и все время. Выражаем их: 
Очевидно, что время движения на участке во втором случае и время движения на участке в первом случае различны.
В первом случае, поскольку нам неизвестны времена 





Подставляем выраженные величины в исходные уравнения.
Таким образом, в первой задаче имеем:
После преобразования получаем:
Во втором случае получаем 
Ответы, как и было предсказано, различны, но во втором случае мы получили, что средняя скорость действительно равняется полусумме скоростей.
Может возникнуть вопрос, а почему сразу нельзя воспользоваться этим уравнением и дать такой ответ?
Дело в том, что записав, что средняя скорость на участке во втором случае равна полусумме скоростей на первом и на втором участках, мы бы представили не решение задачи, а готовый ответ . Решение же, как видно, достаточно длинное, и начинается оно с определяющего уравнения. То, что мы в данном случае получили уравнение, которое хотели использовать изначально – чистая случайность.
При неравномерном движении скорость тела может непрерывно меняться. При таком движении скорость в любой последующей точке траектории будет отличаться от скорости в предыдущей точке.
Скорость тела в данный момент времени и в данной точке траектории называют мгновенной скоростью .
Чем больше промежуток времени Δ, тем средняя скорость больше отличается от мгновенной. И, наоборот, чем меньше промежуток времени, тем меньше средняя скорость отличается от интересующей нас мгновенной скорости.
Физическая величина, равная отношению достаточно малого перемещения на участке траектории (либо пройденного пути), к малому промежутку времени, в течение которого совершается это перемещение (либо проходится путь), называется мгновенной скоростью .
Определим мгновенную скорость как предел, к которому стремится средняя скорость на бесконечно малом промежутке времени :
Если речь идет о средней скорости перемещения, то мгновенная скорость является величиной векторной:
Если речь идет о средней скорости прохождения пути, то мгновенная скорость является величиной скалярной:
Часто встречаются случаи, когда при неравномерном движении скорость тела меняется за равные промежутки времени на одну и ту же величину.
Движение тела, при котором скорость тела за любые равные промежутки времени изменяется на одну и ту же величину, называется равнопеременным .
Соответственно, если скорость тела за любые равные промежутки времени не изменяется на одинаковую величину, то движение будет называться неравнопеременным .
При равнопеременном движении скорость тела может, как уменьшаться, так и увеличиваться.
Если скорость тела увеличивается, то движение называется равноускоренным, а если уменьшается – равнозамедленным.
Характеристикой равнопеременного движения служит физическая величина, называемая ускорением .
Ускорение – это векторная физическая величина, равная отношению изменения скорости тела ко времени, в течение которого это изменение произошло:
Ускорение при равнопеременном движении не зависит ни от изменения скорости, ни от времени изменения скорости.
Ускорение показывает, на сколько изменяется скорость тела за единицу времени.
Чтобы получить единицу ускорения, надо в определяющую формулу ускорения подставить единицы скорости – 1 м/с и времени – 1 с. Получаем: [] = 1 м/с 2 .
Зная ускорение тела и его начальную скорость, можно найти скорость в любой наперед заданный момент времени:
В проекции на координатную ось уравнение примет вид: υ = υ0 + ∙ Δ.
🌟 Видео
Мгновенная скорость (видео 6)| Векторы. Прямолинейное движение | ФизикаСкачать

Решение графических задач на равномерное движениеСкачать

УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать

Неравномерное движениеСкачать

РАВНОМЕРНОЕ ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ | скорость движения | УРАВНЕНИЕ ДВИЖЕНИЯСкачать

Урок 24. Мгновенная скорость. Равноускоренное движение. УскорениеСкачать

Прямолинейное неравномерное движениеСкачать

Физика 10 класс (Урок№2 - Равномерное прямолинейное движение материальной точки.)Скачать

Прямолинейное равномерное и неравномерное движение. Практ. часть - решение задачи. 1 часть. 7 класс.Скачать

9 класс, 3 урок, Графики прямолинейного равномерного движенияСкачать

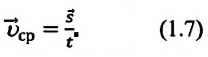
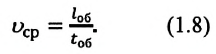
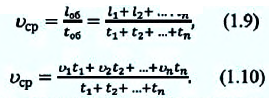
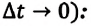
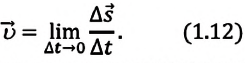
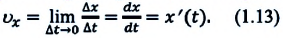
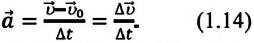
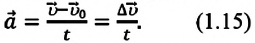
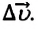
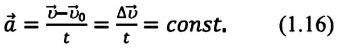
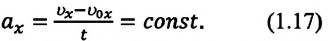
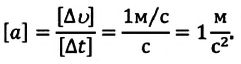

 где – весь путь, а – все время движения на рассматриваемом участке.
где – весь путь, а – все время движения на рассматриваемом участке.











