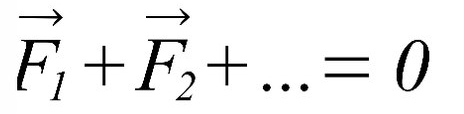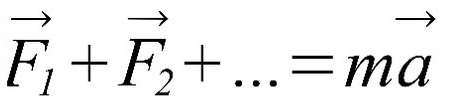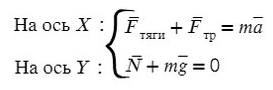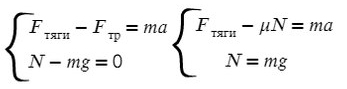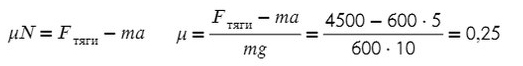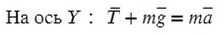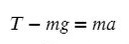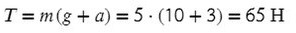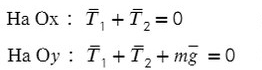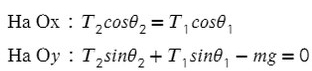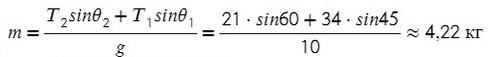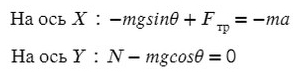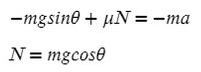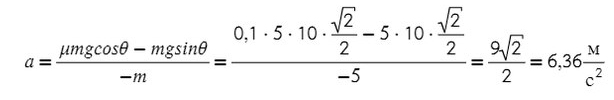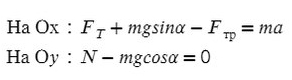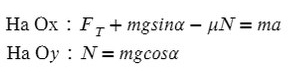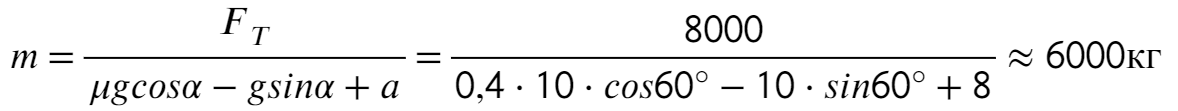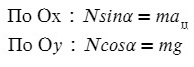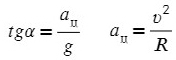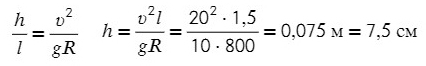Уравнение движения на наклонной плоскости

Динамика и кинематика — это два важных раздела физики, которые изучают законы перемещения объектов в пространстве. Первый рассматривает действующие на тело силы, второй же занимается непосредственно характеристиками динамического процесса, не вникая в причины того, что его вызвало. Знание этих разделов физики необходимо применять для успешного решения задач на движение по наклонной плоскости. Рассмотрим этот вопрос в статье.

Видео:ДВИЖЕНИЕ ПО НАКЛОННОЙ ПЛОСКОСТИ | механика 10 классСкачать

Основная формула динамики

Конечно же, речь идет о втором законе, который постулировал Исаак Ньютон в XVII веке, изучая механическое движение твердых тел. Запишем его в математической форме:

Действие внешней силы F¯ вызывает появление линейного ускорения a¯ у тела с массой m. Обе векторные величины (F¯ и a¯) направлены в одну и ту же сторону. Сила в формуле является результатом действия на тело всех сил, которые присутствуют в системе.

В случае движения вращения второй закон Ньютона записывается в виде:

Здесь M и I — моменты силы и инерции, соответственно, α — угловое ускорение.

Видео:Наклонная плоскость. Расстановка сил | 50 уроков физики (6/50)Скачать

Формулы кинематики

Решение задач на движение по наклонной плоскости требует знания не только главной формулы динамики, но и соответствующих выражений кинематики. Они связывают в равенства ускорение, скорость и пройденный путь. Для равноускоренного (равнозамедленного) прямолинейного движения применяются следующие формулы:

Здесь v₀ — значение начальной скорости тела, S — пройденный за время t путь вдоль прямолинейной траектории. Знак «+» следует поставить, если скорость тела увеличивается с течением времени. В противном случае (равнозамедленное движение) следует использовать в формулах знак «-«. Это важный момент.

Если движение осуществляется по круговой траектории (вращение вокруг оси), тогда следует использовать такие формулы:

Здесь α и ω — угловые ускорение и скорость, соответственно, θ — угол поворота вращающегося тела за время t.

Линейные и угловые характеристики друг с другом связаны формулами:

Здесь r — радиус вращения.

Видео:Урок 87. Движение по наклонной плоскости (ч.1)Скачать

Движение по наклонной плоскости: силы

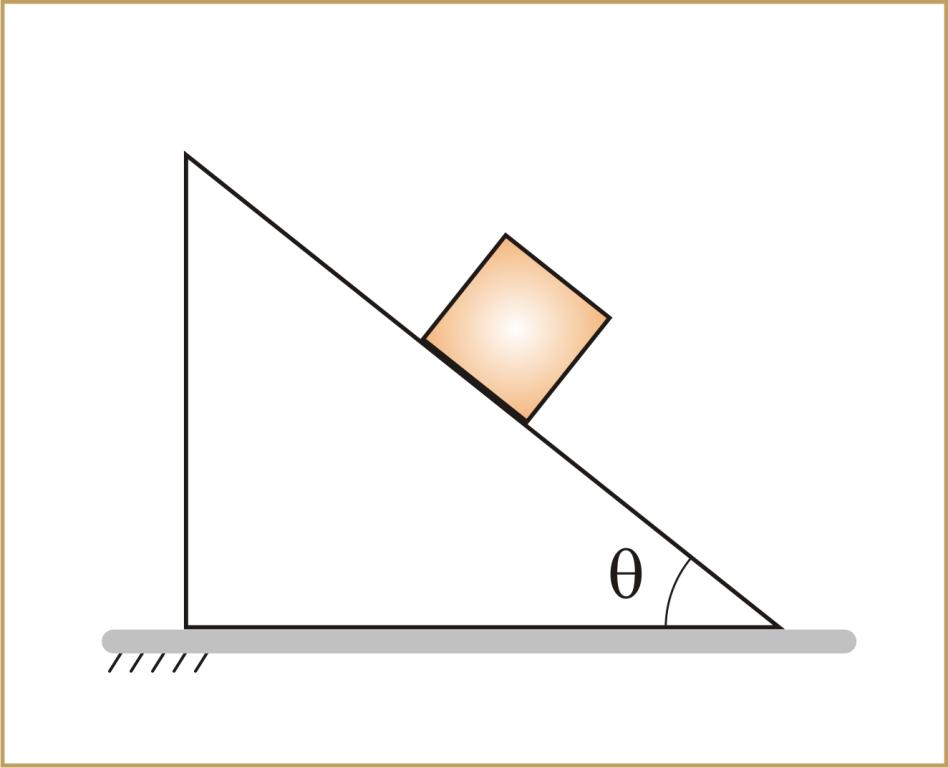
Под этим движением понимают перемещение некоторого объекта вдоль плоской поверхности, которая наклонена под определенным углом к горизонту. Примерами может служить соскальзывание бруска по доске или качение цилиндра по металлическому наклоненному листу.

Для определения характеристик рассматриваемого типа движения необходимо в первую очередь найти все силы, которые действуют на тело (брусок, цилиндр). Они могут быть разными. В общем случае это могут быть следующие силы:

• тяжести;
• реакции опоры;
• трения качения и/или скольжения;
• натяжение нити;
• сила внешней тяги.

Первые три из них присутствуют всегда. Существование последних двух зависит от конкретной системы физических тел.

Чтобы решать задачи на перемещение по плоскости наклонной необходимо знать не только модули сил, но и их направления действия. В случае, если тело по плоскости скатывается, сила трения неизвестна. Однако она определяется из соответствующей системы уравнений движения.

Видео:Движение тела по наклонной плоскостиСкачать

Методика решения

Решения задач данного типа начинается с определения сил и их направлений действия. Для этого в первую очередь рассматривают силу тяжести. Ее следует разложить на два составляющих вектора. Один из них должен быть направлен вдоль поверхности наклонной плоскости, а второй должен быть ей перпендикулярен. Первая составляющая силы тяжести, в случае движения тела вниз, обеспечивает его линейное ускорение. Это происходит в любом случае. Вторая равна силе реакции опоры. Все эти показатели могут иметь различные параметры.

Сила трения при движении по наклонной плоскости всегда направлена против перемещения тела. Если речь идет о скольжении, то вычисления довольно просты. Для этого следует использовать формулу:

Где N — реакция опоры, µ — коэффициент трения, не имеющий размерности.

Если в системе присутствуют только указанные три силы, тогда их результирующая вдоль наклонной плоскости будет равна:

Здесь φ — это угол наклона плоскости к горизонту.

Зная силу F, можно по закону Ньютона определить линейное ускорение a. Последнее, в свою очередь, используется для определения скорости движения по наклонной плоскости через известный промежуток времени и пройденного телом расстояния. Если вникнуть, то можно понять, что все не так уж и сложно.

В случае, когда тело скатывается по наклонной плоскости без проскальзывания, суммарная сила F будет равна:

Где F_r — сила трения качения. Она неизвестна. Когда тело катится, то сила тяжести не создает момента, поскольку приложена к оси вращения. В свою очередь, F_r создает следующий момент:

Учитывая, что мы имеем два уравнения и две неизвестных (α и a связаны друг с другом), можно легко решить эту систему, а значит, и задачу.

Теперь рассмотрим, как использовать описанную методику при решении конкретных задач.

Видео:Урок 88. Движение по наклонной плоскости (ч.2)Скачать

Задача на движение бруска по наклонной плоскости

Деревянный брусок находится в верхней части наклонной плоскости. Известно, что она имеет длину 1 метр и располагается под углом 45 o . Необходимо вычислить, за какое время брусок опустится по этой плоскости в результате скольжения. Коэффициент трения принять равным 0,4.

Записываем закон Ньютона для данной физической системы и вычисляем значение линейного ускорения:

a = g*(sin(φ) — µ*cos(φ)) ≈ 4,162 м/с 2

Поскольку нам известно расстояние, которое должен пройти брусок, то можно записать следующую формулу для пути при равноускоренном движении без начальной скорости:

Откуда следует выразить время, и подставить известные значения:

Таким образом, время движения по наклонной плоскости бруска составит меньше секунды. Заметим, что полученный результат от массы тела не зависит.

Видео:ЗАДАЧИ НА НАКЛОННУЮ ПЛОСКОСТЬ - не ГРОБ! КАК ТАКИЕ РЕШАТЬ?Скачать

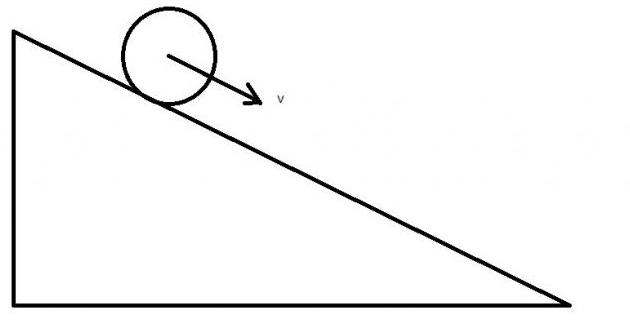
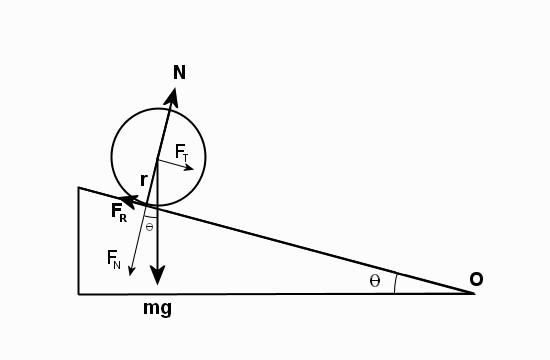
Задача со скатывающимся по плоскости цилиндром

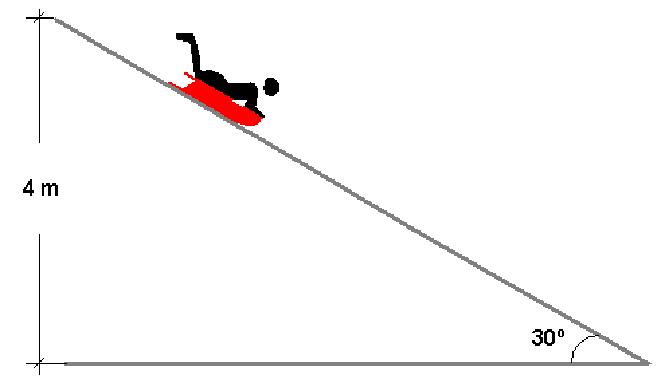
Цилиндр радиусом 20 см и массой 1 кг помещен на наклонную под углом 30 o плоскость. Следует вычислить его максимальную линейную скорость, которую он наберет при скатывании с плоскости, если ее длина составляет 1,5 метра.

Запишем соответствующие уравнения:

Момент инерции I цилиндра вычисляется по формуле:

Подставим это значение во вторую формулу, выразим из нее силу трения F_r и заменим полученным выражением ее в первом уравнении, имеем:

m*g*sin(φ) — 1/2*m*a = m*a =>

Мы получили, что линейное ускорение не зависит от радиуса и массы скатывающегося с плоскости тела.

Зная, что длина плоскости составляет 1,5 метра, найдем время движения тела:

Тогда максимальная скорость движения по наклонной плоскости цилиндра будет равна:

Подставляем все известные из условия задачи величины в конечную формулу, получаем ответ: v ≈ 3,132 м/c.

Видео:9 класс, 23 урок, Движение тел по наклонной плоскостиСкачать

Уравнение движения на наклонной плоскости

Задачи по динамике.

I и II закон Ньютона.

Ввод и направление осей.

Проецирование сил на оси.

Решение систем уравнений.

Самые типовые задачи по динамике

Начнем с I и II законов Ньютона.

Откроем учебник физики и прочтем. I закон Ньютона: существуют такие инерциальные системы отсчета в которых. Закроем такой учебник, я тоже не понимаю. Ладно шучу, понимаю, но объясню проще.

I закон Ньютона: если тело стоит на месте либо движется равномерно (без ускорения), сумма действующих на него сил равна нулю.

Вывод: Если тело движется с постоянной скоростью или стоит на месте векторная сумма сил будет ноль.

II закон Ньютона: если тело движется равноускоренно или равнозамедленно (с ускорением), сумма сил, действующих на него, равна произведению массы на ускорение.

Вывод: Если тело двигается с изменяющейся скоростью, то векторная сумма сил, которые как-то влияют на это тело ( сила тяги, сила трения, сила сопротивления воздуха), равна массе этого тело умножить на ускорение.

При этом одно и то же тело чаще всего движется по-разному (равномерно или с ускорением) в разных осях. Рассмотрим именно такой пример.

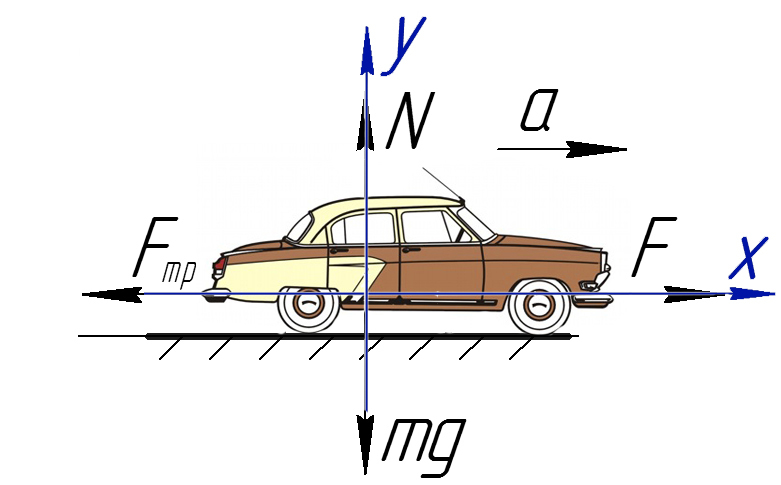
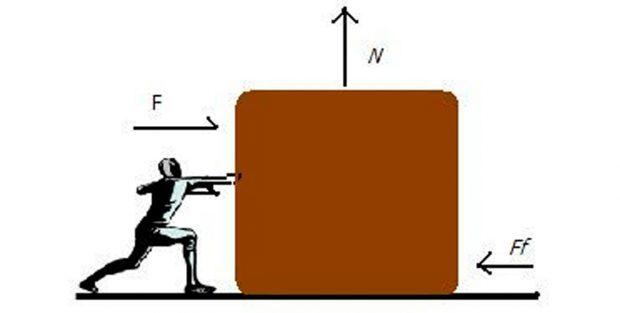
Задача 1. Определите коэффициент трения шин автомобиля массой 600 кг, если сила тяги двигателя 4500 Н вызывает ускорение 5 м/с².

Обязательно в таких задачах делать рисунок, и показывать силы, которые дествуют на машину:

На Ось Х: движение с ускорением

На Ось Y: нет движения (здесь координата, как была ноль так и останется, машина не поднимает в горы или спускается вниз)

Те силы, направление которых совпадает с направлением осей, будут с плюсом, в противоположном случае — с минусом.

По оси X: сила тяги направлена вправо, так же как и ось X, ускорение так же направлено вправо.

Fтр = μN, где N — сила реакции опоры. На оси Y: N = mg, тогда в данной задаче Fтр = μmg.

Коэффициент трения — безразмерная величина. Следовательно, единиц измерения нет.

Задача 2. Груз массой 5кг, привязанный к невесомой нерастяжимой нити, поднимают вверх с ускорением 3м/с². Определите силу натяжения нити.

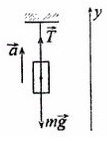
Сделаем рисунок, покажем силы, которые дествуют на груз

T — сила натяжения нити

На ось X: нет сил

Разберемся с направлением сил на ось Y:

Выразим T (силу натяжения) и подставим числительные значения:

Самое главное не запутаться с направлением сил (по оси или против), все остальное сделает калькулятор или всеми любимый столбик.

Далеко не всегда все силы, действующие на тело, направлены вдоль осей.

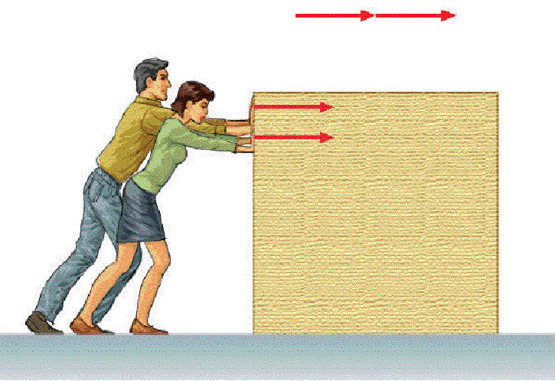
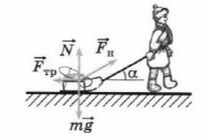
Простой пример: мальчик тянет санки

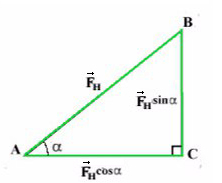
Если мы так же построим оси X и Y, то сила натяжения (тяги) не будет лежать ни на одной из осей.

Чтобы спроецировать силу тяги на оси, вспомним прямоугольный треугольник.

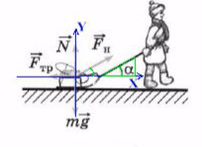
Отношение противолежащего катета к гипотенузе — это синус.

Отношение прилежащего катета к гипотенузе — это косинус.

Сила тяги на ось Y — отрезок (вектор) BC.

Сила тяги на ось X — отрезок (вектор) AC.

Если это непонятно, посмотрите задачу №4.

Чем длинее будет верека и, соответсвенно, меньше угол α, тем проще будет тянуть санки. Идеальный вариант, когда веревка параллельна земле , ведь сила, которая действуют на ось X— это Fнcosα. При каком угле косинус максимален? Чем больше будет этот катет, тем сильнее горизонтальная сила.

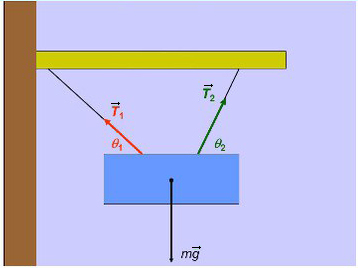
Задача 3. Брусок подвешен на двух нитях. Сила натяжения первой составляет 34 Н, второй — 21Н, θ1 = 45°, θ2 = 60°. Найдите массу бруска.

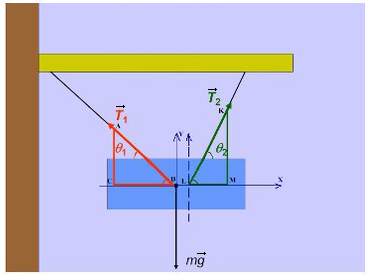
Введем оси и спроецируем силы:

Получаем два прямоугольных треугольника. Гипотенузы AB и KL — силы натяжения. LM и BC — проекции на ось X, AC и KM — на ось Y.

Задача 4. Брусок массой 5 кг (масса в этой задаче не нужна, но, чтобы в уравнениях все было известно, возьмем конкретное значение) соскальзывает с плоскости, которая наклонена под углом 45°, с коэффициентом трения μ = 0,1. Найдите ускорение движения бруска?

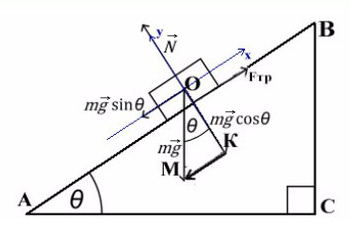
Когда же есть наклонная плоскость, оси (X и Y) лучше всего направить по направлению движения тела. Некоторые силы в данном случае ( здесь это mg) не будут лежать ни на одной из осей. Эту силу нужно спроецировать, чтобы она имела такое же направление, как и взятые оси.
Всегда ΔABC подобен ΔKOM в таких задачах (по прямому углу и углу наклона плоскости).

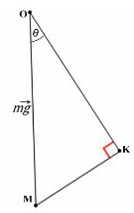
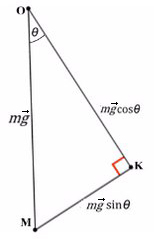
Рассмотрим поподробнее ΔKOM:

Получим, что KO лежит на оси Y, и проекция mg на ось Y будет с косинусом. А вектор MK коллинеарен (параллелен) оси X, проекция mg на ось X будет с синусом, и вектор МК направлен против оси X (то есть будет с минусом).

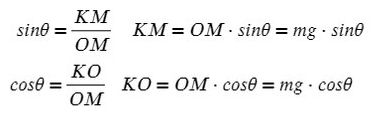
Не забываем, что, если направления оси и силы не совпадают, ее нужно взять с минусом!

Из оси Y выражаем N и подставляем в уравнение оси X, находим ускорение:

Как видно, массу в числителе можно вынести за скобки и сократить со знаменаталем. Тогда знать ее не обязательно, получить ответ реально и без нее.
Да-да, в идеальных условиях (когда нет силы сопротивления воздуха и т.п.), что перо, что гиря скатятся (упадут) за одно и тоже время.

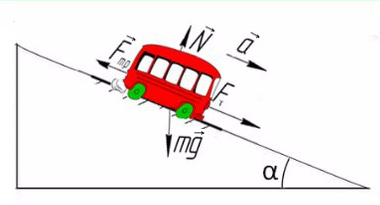
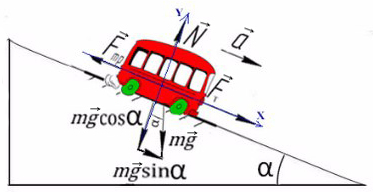
Задача 5. Автобус съезжает с горки под уклоном 60° с ускорением 8 м/с² и с силой тяги 8 кН. Коэффициент трения шин об асфальт равен 0,4. Найдите массу автобуса.

Сделаем рисунок с силами:

Введем оси X и Y. Спроецируем mg на оси:

Запишем второй закон Ньютона на X и Y:

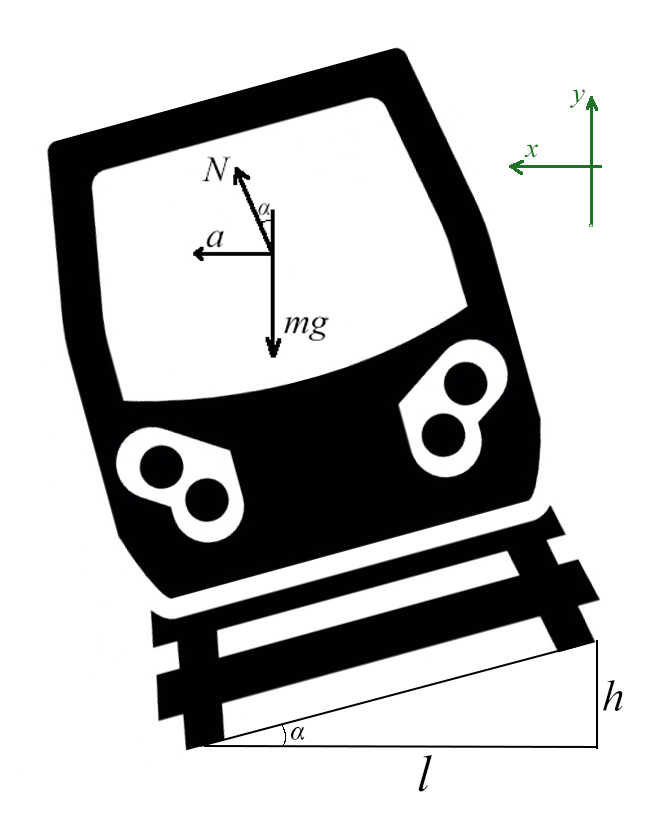
Задача 6. Поезд движется по закруглению радиуса 800 м со скоростью 72 км/ч. Определить, на сколько внешний рельс должен быть выше внутреннего. Расстояние между рельсами 1,5 м.

Самое сложное — понять, какие силы куда действуют, и как угол влияет на них.

Вспомни, когда едешь по кругу на машине или в автобусе, куда тебя выталкивает? Для этого и нужен наклон, чтобы поезд не упал набок!

Угол α задает отношение разницы высоты рельсов к расстоянию между ними (если бы рельсы находились горизонтально)

Запишем какие силы действуют на оси:

Ускорение в данной задачи центростремительное!

Поделим одно уравнение на другое:

Тангенс — это отношение противолежащего катета к прилежащему:

Как мы выяснили, решение подобных задач сводится к расстановке направлений сил, проецированию их на оси и к решению систем уравнений, почти сущий пустяк.

В качестве закрепления материала решите несколько похожих задач с подсказками и ответами.

Видео:Физика. 9 класс. Движение по наклонной плоскостиСкачать

Физика: движение тела по наклонной плоскости. Примеры решения и задачи

Динамика является одним из важных разделов физики, который изучает причины движения тел в пространстве. В данной статье рассмотрим с точки зрения теории одну из типичных задач динамики — движение тела по наклонной плоскости, а также приведем примеры решений некоторых практических проблем.

Видео:Наклонная плоскостьСкачать

Основная формула динамики

Прежде чем переходить к изучению физики движения тела по плоскости наклонной, приведем необходимые теоретические сведения для решения этой задачи.

В XVII Исаак Ньютон благодаря практическим наблюдениям за движением макроскопических окружающих тел вывел три закона, носящих в настоящее время его фамилию. На этих законах зиждется вся классическая механика. Нас интересует в данной статье лишь второй закон. Его математический вид приведен ниже:

Вам будет интересно: Эйлера теорема. Теорема Эйлера для простых многогранников

Формула говорит о том, что действие внешней силы F¯ придаст ускорение a¯ телу массой m. Это простое выражение будем далее использовать для решения задач движения тела по плоскости наклонной.

Отметим, что сила и ускорение — это величины векторные, направленные в одну и ту же сторону. Кроме того, сила — это аддитивная характеристика, то есть в приведенной формуле F¯ можно рассматривать как результирующее воздействие на тело.

Видео:Движение по наклонной плоскости | Физика в анимациях | s02e07Скачать

Наклонная плоскость и силы, действующие на тело, находящееся на ней

Вам будет интересно: Афанасьевская культура: локализация, датировка, носители

Ключевым моментом, от которого зависит успех решения задач движения тела по плоскости наклонной, является определение действующих на тело сил. Под определением сил понимают знание их модулей и направлений действия.

Ниже дан рисунок, где показано, что тело (автомобиль) находится в покое на наклоненной под углом к горизонту плоскости. Какие силы на него действуют?

Список ниже перечисляет эти силы:

• тяжести;
• реакции опоры;
• трения;
• натяжения нити (если присутствует).

Далее опишем подробнее каждую из них применительно к рассматриваемой задаче.

Видео:Динамика тела на наклонной плоскости | Физика ЕГЭ 2023 | УмскулСкачать

Сила тяжести

Вам будет интересно: Антрополог Станислав Владимирович Дробышевский: биография и научная деятельность

В первую очередь это сила тяжести (Fg). Она направлена вертикально вниз. Поскольку тело имеет возможность двигаться только вдоль поверхности плоскости, то при решении задач силу тяжести разлагают на две взаимно перпендикулярные составляющие. Одна из составляющих направлена вдоль плоскости, другая — перпендикулярна ей. Только первая из них приводит к появлению у тела ускорения и, по сути, является единственным движущим фактором для рассматриваемого тела. Вторая составляющая обуславливает возникновение силы реакции опоры.

Видео:Движение по наклонной плоскости (продожение1)Скачать

Реакция опоры

Второй действующей на тело силой является реакция опоры (N). Причина ее появления связана с третьим законом Ньютона. Величина N показывает, с какой силой плоскость воздействует на тело. Она направлена вверх перпендикулярно плоскости наклонной. Если бы тело находилось на горизонтальной поверхности, то N равнялась бы его весу. В рассматриваемом же случае N равна лишь второй составляющей, полученной при разложении силы тяжести (см. абзац выше).

Реакция опоры не оказывает прямого воздействия на характер движения тела, поскольку она перпендикулярна плоскости наклона. Тем не менее она обуславливает появление трения между телом и поверхностью плоскости.

Видео:Физика. Динамика. Тело на наклонной плоскости 2Скачать

Сила трения

Третьей силой, которую следует учитывать при исследовании движения тела по наклонной плоскости, является трение (Ff). Физическая природа трения является непростой. Ее появление связано с микроскопическими взаимодействиями соприкасающихся тел, имеющих неоднородные поверхности контакта. Выделяют три вида этой силы:

Трение покоя и скольжения описываются одной и той же формулой:

где µ — это безразмерный коэффициент, значение которого определяется материалами трущихся тел. Так, при трении скольжения дерева о дерево µ = 0,4, а льда о лед — 0,03. Коэффициент для трения покоя всегда больше такового для скольжения.

Трение качения описывается по отличной от предыдущей формуле. Она имеет вид:

Здесь r — радиус колеса, f — коэффициент, имеющий размерность обратной длины. Эта сила трения, как правило, намного меньше предыдущих. Заметим, что на ее значение влияет радиус колеса.

Сила Ff, какого бы типа она ни была, всегда направлена против движения тела, то есть Ff стремится остановить тело.

Видео:Наклонная плоскость. ФизикаСкачать

Натяжение нити

При решении задач движения тела по наклонной плоскости эта сила не всегда присутствует. Ее появление определяется тем, что находящееся на наклонной плоскости тело связано с помощью нерастяжимой нити с другим телом. Часто второе тело свисает на нити через блок за пределами плоскости.

На находящийся на плоскости предмет, сила натяжение нити воздействует либо ускоряя его, либо замедляя. Все зависит от модулей сил, действующих в физической системе.

Появление этой силы в задаче значительно усложняет процесс решения, поскольку приходится рассматривать одновременно движение двух тел (на плоскости и свисающего).

Далее приведем пример решения двух задач без участия силы натяжения нити.

Видео:Лаборатория "Механика", Движение тела по наклонной плоскостиСкачать

Задача на определение критического угла

Теперь пришло время применить описанную теорию для решения реальных задач движения по наклонной плоскости тела.

Предположим, что брус из дерева имеет массу 2 кг. Он находится на деревянной плоскости. Следует определить, при каком критическом угле наклона плоскости брус начнет по ней скользить.

Скольжение бруса наступит только тогда, когда суммарная действующая вниз вдоль плоскости сила на него окажется больше нуля. Таким образом, чтобы решить эту задачу, достаточно определить результирующую силу и найти угол, при котором она станет больше нуля. Согласно условию задачи на брус будут вдоль плоскости оказывать действие только две силы:

• составляющая силы тяжести Fg1;
• трение покоя Ff.

Чтобы началось скольжение тела, должно выполняться условие:

Отметим, что если составляющая силы тяжести превысит трение покоя, то она также будет больше силы трения скольжения, то есть начавшееся движение будет продолжаться с постоянным ускорением.

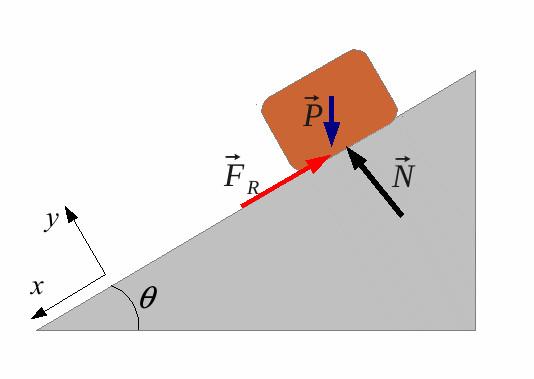
Рисунок ниже показывает направления всех действующих сил.

Обозначим критический угол символом θ. Несложно показать, что силы Fg1 и Ff будут равны:

Fg1 = m × g × sin(θ);

Ff = µ × m × g × cos(θ).

Здесь m × g — это вес тела, µ — коэффициент силы трения покоя для пары материалов дерево-дерево. Из соответствующей таблицы коэффициентов можно найти, что он равен 0,7.

Подставляем найденные величины в неравенство, получаем:

m × g × sin(θ) ≥ µ × m × g × cos(θ).

Преобразуя это равенство, приходим к условию движения тела:

Мы получили весьма интересный результат. Оказывается, значение критического угла θ не зависит от массы тела на наклонной плоскости, а однозначно определяется коэффициентом трения покоя µ. Подставляя его значение в неравенство, получим величину критического угла:

θ ≥ arctg(0,7) ≈ 35o.

Видео:Скатывание цилиндров с наклонной плоскостиСкачать

Задача на определение ускорения при движении по наклонной плоскости тела

Теперь решим несколько иную задачу. Пусть на стеклянной наклонной плоскости находится брус из дерева. Плоскость к горизонту наклонена под углом 45o. Следует определить, с каким ускорением будет двигаться тело, если его масса равна 1 кг.

Запишем главное уравнение динамики для этого случая. Поскольку сила Fg1 будет направлена вдоль движения, а Ff против него, то уравнение примет вид:

Подставляем полученные в предыдущей задаче формулы для сил Fg1 и Ff, имеем:

m × g × sin(θ) — µ × m × g × cos(θ) = m × a.

Откуда получаем формулу для ускорения:

a = g × (sin(θ) — µ × cos(θ)).

Снова мы получили формулу, в которой нет массы тела. Этот факт означает, что бруски любой массы будут соскальзывать за одно и то же время по наклонной плоскости.

Учитывая, что коэффициент µ для трущихся материалов дерево-стекло равен 0,2, подставим все параметры в равенство, получим ответ:

Таким образом, методика решения задач с наклонной плоскостью заключается в определении результирующей силы, действующей на тело, и в последующем применении второго закона Ньютона.

💥 Видео

движение по наклонной плоскости без тренияСкачать

Скатывание тела (колеса, цилиндра) по наклонной плоскостиСкачать

Работа при движении по наклонной плоскостиСкачать

Движение по наклонной плоскости ("Горка")Скачать