§2 Пружинный маятник.
Упругие и квазиупругие силы .
Уравнение колеблющейся пружины

1) величина силы пропорциональна величине отклонения системы от положения равновесия
2) направление сила противоположно направлении смещения, т.е. сила всегда направлена к положению равновесия (при х > 0, F упр F упр > 0)
3) В положении равновесия х = 0 и F упр = 0.
Систему, состоящую из материальной точки массы m и абсолютно упругой пружины с коэффициентом жесткости k , в которой возможны свободные колебания, называют пружинным маятником.
Запишем второй закон Ньютона для рис. б
Если сила не является по своей природе упругой, но подчиняется закону F = — k х , то она называется квазиупругой силой.
Получим уравнение пружинного маятника. Учтем в записи второго закона Ньютона, что
— дифференциальное уравнение точки, совершающей колебательное движение (дифференциальное уравнение пружинного маятника).
Решение дифференциального уравнения:
— уравнение колеблющейся точки (уравнение колеблющейся пружины).
— собственная частота колебаний.
§3 Математический и физический маятники.
Периоды колебаний математического и физического маятников
Математический маятник — материальная точка, подвешенная на невесомой нерастяжимой нити, и совершавшая колебания в вертикальной плоскости под действием силы тяжести. Материальная точка — тело, масса которого сосредоточена в центре масс и размерами которого в условиях данной задачи, можно пренебречь.


Основное уравнение вращательного цветения запишется в виде

М – момент сил, I – момент инерции, ε – угловое ускорение.
Равнодействующая сил 


Из треугольника АВС
таким образом, колебания математического маятника происходят под действием квазиупругой силы — силы тяжести.
Тогда (1) запишется в виде

Знак минус учитывает, что векторы 




Сократив в (2) на m и 
При малых углах колебаний α = 5 ÷6° , 
получим дифференциальное уравнение колебаний математического маятника
— уравнение математического маятника.
из которого видно, что угол α изменяется по закону косинуса. α0 — амплитуда, ω0 — циклическая частота, φ0 — начальная фаза.
— период колебаний математического маятника
Физический маятник — твердое тело, колеблющееся под действием силы тяжести вокруг неподвижной горизонтальной оси, не проходящей через центр тяжести тела, называемой осью качания маятника.

При малых углах колебаний 
— дифференциальное уравнение физического маятника.
— период колебаний физического маятника
следовательно, математический маятник с длиной
Видео:Основное уравнение динамики вращательного движения. 10 класс.Скачать

Уравнение движения маятника второй закон ньютона
«Физика — 11 класс»
Колебания тела можно описать, используя законы Ньютона.
Уравнение движения тела, колеблющегося под действием силы упругости.
Согласно второму закону Ньютона произведение массы тела на ускорение его равно равнодействующей всех сил, приложенных к телу:
Запишем уравнение движения для шарика, движущегося прямолинейно вдоль горизонтали под действием силы упругости Fупр пружины.
Направим ось ОХ вправо. Пусть начало отсчета координат соответствует положению равновесия шарика.
В проекции на ось ОХ уравнение движения можно записать так:
где ах и Fx упр — проекции ускорения и силы упругости пружины на эту ось.
Согласно закону Гука проекция Fx ynp прямо пропорциональна смещению шарика из положения равновесия.
Смещение же равно координате х шарика, причем проекция силы и координата имеют противоположные знаки. Следовательно,
Fx yпp = -kх
Разделив левую и правую части уравнения на массу, получим уравнение, описывающее колебания тела под действием силы упругости:
Проекция ускорения тела прямо пропорциональна его координате, взятой с противоположным знаком.
Так как масса и жесткость пружины — постоянные величины, то их отношение также постоянная величина.
Уравнение движения математического маятника
При колебаниях маятника на нерастяжимой нити он все время движется по дуге окружности, радиус которой равен длине нити l.
Положение маятника в любой момент времени определяется одной величиной — углом альфа (α) отклонения нити от вертикали.
Пусть угол α>0, если маятник отклонен вправо от положения равновесия,
и α 0) составляющая силы тяжести Ft направлена влево и ее проекция отрицательна: Ft 0.
Проекция ускорения маятника на касательную к его траектории аt характеризует быстроту изменения модуля скорости маятника.
Поступая налогично выводу форулы для маятника, колеблющегося под действием силы упругости,
получим уравнение движения для математического маятника (нитяного маятника):
Проекция ускорения тела прямо пропорциональна его координате, взятой с противоположным знаком.
где
l — длина нити маятника,
g — ускорение свободного падения,
х — смещение маятника.
Вывод:
Движение маятника на пружине и колебания маятника на нити происходят одинаковым образом, хотя силы, вызывающие колебания, имеют различную физическую природу.
Ускорение прямо пропорционально координате (смещению от положения равновесия).
Колебания в этих двух случаях совершаются под действием сил, равнодействующая которых прямо пропорциональна смещению колеблющегося тела от положения равновесия и направлена в сторону, противоположную этому смещению.
Источник: «Физика — 11 класс», учебник Мякишев, Буховцев, Чаругин
Механические колебания. Физика, учебник для 11 класса — Класс!ная физика
Видео:Классические уравнения | математический маятник | вывод через второй закон НьютонаСкачать

Математического маятника
Измерение ускорения свободного падения с помощью
Ускорением свободного падения 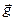
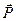
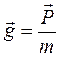
Сила тяжести приложена к данному телу и равна геометрической сумме силы тяготения 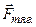
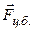
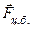
Одним из простых и одновременно достаточно точных методов определения ускорения свободного падения тел g является метод, основанный на использовании математического маятника. Реально математический маятник представляет собой систему, состоящую из маленького шарика, который можно принять за материальную точку массой m, и тонкой невесомой нерастяжимой нити длиной l, подвешенной к неподвижной точке О, рис. 1. При колебании шарика на нерастяжимой нити шарик все время движется по дуге окружности, радиус которой равен l.
В качестве координаты, определяющей положение мятника, совершающего колебания в одной плоскости, можно взять угол между вертикальной линией, проходящей через точку подвеса и нитью маятника. Обозначим этот угол буквой φ. Причем, условимся углы, отсчитываемые вправо от положения равновесия считать положительными, влево – отрицательными.
Для обоснования сущности данного метода воспользуемся вторым законом Ньютона. На маятник массой m действуют две силы: сила тяжести 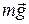
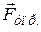
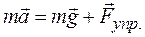

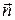
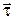
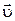
Для нашей цели достаточно спроектировать вектора на направление 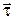
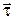
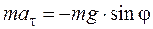
Знак «–» в уравнении (3) справа обусловлен тем, что проекция силы тяжести на касательное направление отрицательна ( 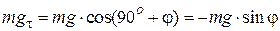
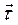
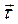
Ограничиваясь малыми углами отклонения маятника, можно sinφ заменить значением угла φ, выраженным в радианах. Так для φ = 10 о = 0,1745 рад получаем: sin(0,1745) ≈ 0,1736. Из этого примера видно, что разница между значением угла φ в радианах и значением синуса этого угла в радианах для угла в 10 о не превышает 0,5%. При меньших значениях угла φ это различие будет еще меньшим, а предложенная замена будет более точной. Поэтому рекомендуется в экспериментах задавать отклонения угла маятника не более 10 о . При этом условии уравнение (3) примет вид:
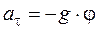
Из школьного курса физики известна связь между линейной и угловой скоростями движения м.т. по окружности:
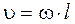
С другой стороны угловая скорость равна первой производной угла поворота φ по времени:
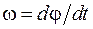
По определению касательного ускорения имеем:
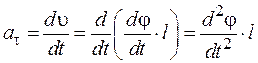
В формуле (7) мы учли определения (5) и (6). Тогда с учетом определений (7) уравнение (4) примет вид:
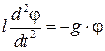
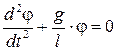
Легко проверить, что размерность множителя 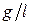
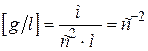
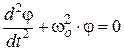
Решением данного уравнения будет гармоническая функция вида:
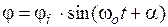
где φо – амплитуда колебаний, α – начальная фаза колебаний. Справедливость этого решения можно проверить его подстановкой в уравнение (9). Если решение (10) верно, то оно превращает уравнение (9) в тождество. Проверку этого решения рекомендуется выполнить студентам самостоятельно.
Циклическая частота колебаний математического маятника, как следует из вывода уравнения (9), определяется выражением: 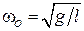
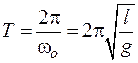
Возведем обе части уравнения (11) в квадрат, получим:
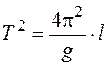
Уравнение (12) подобно уравнению прямой вида: 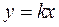
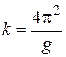
а в качестве переменных x и y соответственно l и T 2 .
Строя график зависимости квадрата периода Т 2 отдлины маятника l мы должны получить линейную зависимость. Определяя тангенс угла наклона этого графика к оси абсцисс (оси l), и используя формулу (13), можем рассчитать ускорения свободного падения:
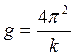
Дата добавления: 2016-03-15 ; просмотров: 948 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
🎦 Видео
1.4. Законы Ньютона как уравнение движения | Динамика | Александр Чирцов | ЛекториумСкачать

Алгоритм решения задач на второй закон Ньютона часть 1| Физика TutorOnlineСкачать

ЭТО ОБЯЗАТЕЛЬНО НУЖНО ЗНАТЬ — Второй Закон Ньютона или от чего зависит ускорение телаСкачать

Взаимодействие тел. Второй закон Ньютона | Физика 10 класс #10 | ИнфоурокСкачать

Второй закон Ньютона | Физика 9 класс #11 | ИнфоурокСкачать

Урок 92 (осн). Колебательное движение. МаятникиСкачать

Второй закон НьютонаСкачать

Три Закона Ньютона. Простое ОбъяснениеСкачать

Второй закон Ньютона. Практическая часть. 9 класс.Скачать

Математические и пружинные маятники. 11 класс.Скачать

Период колебаний математического маятника 🧬 #shorts #умскул_физика #егэ2023 #егэфизикаСкачать

Урок 52. Масса и ее измерение. Сила. Второй закон Ньютона. Равнодействующая.Скачать

Откуда берётся формула математического маятника?🤯🤯🤯Скачать

Решение задач по теме Законы НьютонаСкачать

математический маятник ЕГЭ ФИЗИКА колебания частота периодСкачать

Урок 93. Основное уравнение динамики вращательного движенияСкачать

Колебания математического маятникаСкачать

Законы Ньютона. Практическая часть. 10 класс.Скачать





































