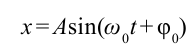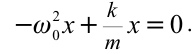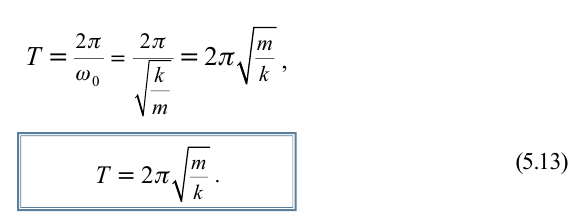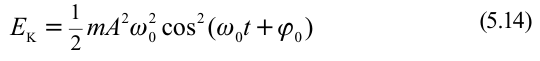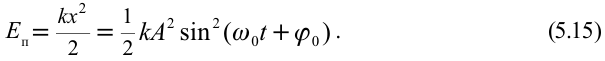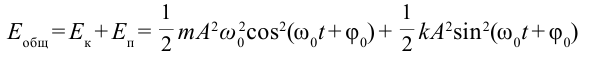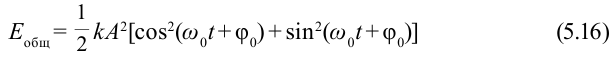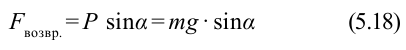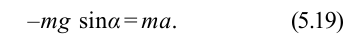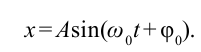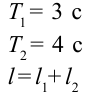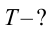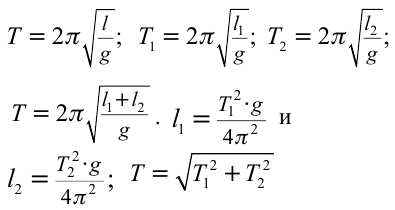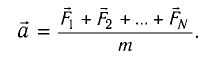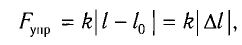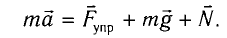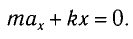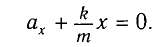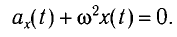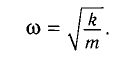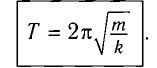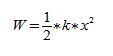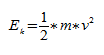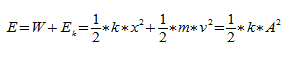Уравнение движения массы m некоторого пружинного маятника имеет вид mx rx kx 0

Название	Решение описывает a свободные линейные затухающие колебания Уравнение движения массы m некоторого пружинного маятника имеет вид
Дата	28.03.2022
Размер	83.97 Kb.
Формат файла
Имя файла	Kharisov_I_R_BST2055_Fizika_test.docx
Тип	Решение #422763

Плоская бегущая волна имеет вид =…cos(…t-…x)м.

Ответ: 10-2 cos(5t 0,2x)
17. Точки, находящаяся на расстоянии х₁ = 7м и х₂ = 12м от источника возмущения, колеблются с разностью фаз .Скорость волны 12м/c. Плоская бегущая волна имеет вид:

x)м.

Ответ:
18. Электрическое поле электромагнитной волны в среде с изменяется по закону . Диэлектрическая проницаемость среды ….

Ответ: 4
19. Известно, что впервые дифракцию электронов наблюдали на кристаллах твердых тел. Это связано с тем, что для наблюдения дифракции длина волны де Бройля ( ) должна быть:

С) меньше, но сравнимой с а.
20. Групповая скорость электромагнитных волн определяет скорость переноса энергии волной. Групповая скорость волн де-Бройля равна

В) классической скорости движения микрообъектов.
21. Фазовая скорость (υ_Б) волны де-Бройля ψ_Б

D) не имеет физического смысла, т.к. физическим содержанием обладает только |ψ_Б | 2 и υ_Б > c.

22.Внешний фотоэффект — это:

С) Эмиссия, т.е. выход электронов из приповерхностных слоёв вещества под действием квантов переменного

электромагнитного поля.
23. Если отношение частот для красной границы фотоэффекта двух фотокатодов равно и работа выхода второго равна 2ЭВ, то работа выхода

Ответ: 6 эВ
24. Если переносимый фотонами импульс равен _, то длина волны электромагнитного излучения равна:

В)
25. Если фотоны некоторого электромагнитного поля имеют импульс , то частота этого поля равна:

Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Пружинные и математические маятники в физике — виды, формулы и определения с примерами

Содержание:

Пружинные и математические маятники:

Тело или система тел, совершающие периодические колебательные движения, называются маятниками. Большинство колебательных движений, встречающихся в природе, напоминают движение пружинных и математических маятников.

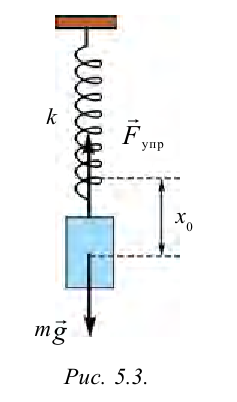
Система, состоящая из груза массой

Если немножко растянуть пружину и отпустить, то груз придет в колебательное движение в вертикальном направлении.
С помощью опытов мы определили, что смещение груза в зависимости от времени изменяется следующbм образом:

Если учесть, что ускорение тела, совершающего гармонические колебания 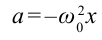, то уравнение (5.10) примет вид:

Из этого уравнения мы имеем:

Значит, частота циклического колебания тела, совершающего гармоническое колебание, зависит от параметров тел, входящих в систему колебания. Формула (5.12) называется формулой для
определения циклической (периодической) частоты пружинного маятника.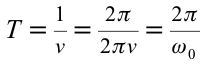

Период колебания пружинного маятника прямо пропорционален выведенному из-под квадратного корня значению массы груза и обратно пропорционален выведенному из-под квадратного корня значению упругости пружины.
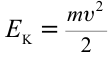
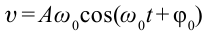
Рассмотрим обмен энергиями в пружинном маятнике. Кинетическая энергия маятника, если не учитывать массу пружины, равна кинетической энергии груза, . В предыдущих темах было показано, что скорость можно выразить формулой . В таком случае кинетическая энергия маятника равна

Потенциальная энергия пружинного маятника равна энергии деформации пружины, т.е.:

В большинстве случаев важно знать полную энергию системы:

Если учесть, что ,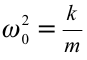

Обратите внимание, что полная энергия пружинного маятника является постоянной величиной, не зависящей от времени, т.е. соблюдается выполнение закона сохранения механической энергии.
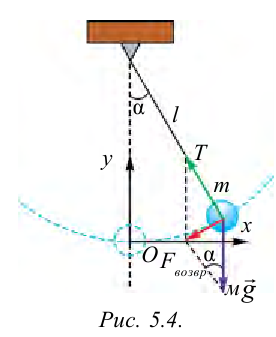
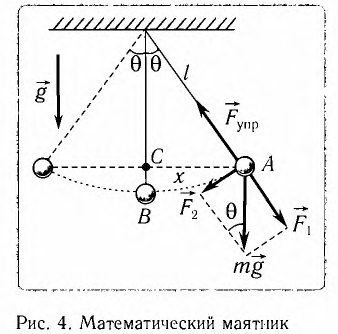
Материальная точка, подвешенная на нерастяжимой и невесомой нити и совершающая периодическое колебательное движение вокруг равновесного состояния, называется математическим маятником.

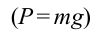
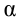
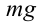
Когда маятник находится в устойчивом равновесном состоянии, вес материальной точки уравновешивает силу натяжения (рис. 5.4), так как их модули равны и направлены по одной линии в противоположные стороны. Если наклонить маятник на угол , силы и не смогут уравновесить друг друга из-за взаимного расположения под углом. В результате сложения таких сил появится возвращающая сила, которая вернет маятник в равновесное состояние. Если отпустить маятник, то под воздействием возвращающей силы он начинает двигаться в сторону равновесного состояния.

Из рис. 5.4. видим, что:

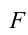
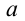
Согласно второму закону Ньютона, сила придает материальной точке ускорение , поэтому

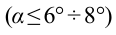
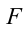
Из-за того, что угол наклона очень маленький , а сила направлена противоположно смещению, формулу (5.19) можно записать в виде

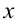
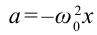
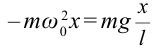
Если смещение материальной точки (шарика) во время колебательного процесса отметить буквой и учитывать соотношение , получим
Следовательно
Исходя из смысла периода колебания и учитывая, что 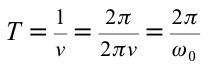получаем

Эта формула, определяющая период колебания математического маятника, называется формулой Гюйгенса. Отсюда вытекают следующие законы математического маятника:

1. при маленьких углах наклона (а) математического маятника, его период колебания не зависит от амплитуды колебания.
2. период колебания математического маятника также не зависит от массы подвешенного на него груза;
3. период колебания математического маятника прямо пропорционален выведенному из-под квадратного корня значению длины маятника и обратно пропорционален выведенному из-под квадратного корня значению ускорения свободного падения.

Отсюда колебание математического маятника записывается следующим выражением:

Следует отметить, что когда амплитуда колебания или угол наклона велики, колебания математического маятника не являются гармоническим. В этом случае нельзя считать 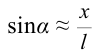и для решения уравнения движения не применяется закон синусов или косинусов.

Пример:

Период колебания первого маятника равен 3 сек, второго – 4 сек. Найдите период колебания маятника с длиной, равной сумме длин этих маятников.

Решение: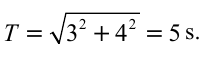

Ответ: 5 cек.

Видео:Физика 9 класс. Уравнение механического движения пружинного маятникаСкачать

Пружинный и математический маятники

Второй закон Ньютона (основной закон динамики): ускорение, приобретаемое материальной точкой, прямо пропорционально равнодействующей всех сил, действующих на нее, и обратно пропорционально массе материальной точки:

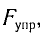
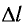
Закон Гука: модуль силы упругости , возникающей в теле при упругих деформациях, прямо пропорционален его абсолютному удлинению (сжатию) :

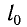
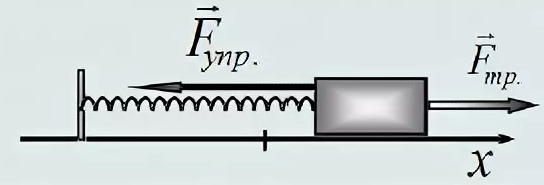
где k — жесткость тела, — длина недеформированного тела, l — длина деформированного тела.

Рассмотрим пружинный маятник, представляющий собой колебательную систему, образованную грузом на пружине.

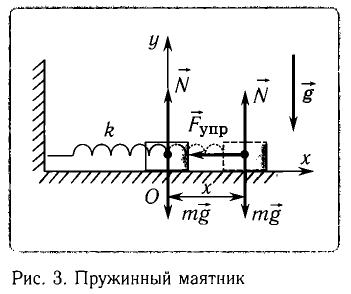
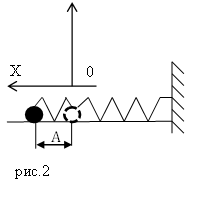
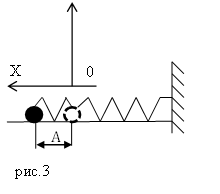
Пусть груз массой т, лежащий на гладкой горизонтальной поверхности, прикреплен к свободному концу невесомой пружины жесткостью k (рис. 3). Второй конец пружины закреплен относительно данной инерциальной системы отсчета (ИСО).

Выведем груз из положения равновесия, сместив его на расстояние х вправо. В пружине возникнет сила упругости 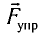направленная влево.

Запишем второй закон Ньютона для движения груза:

В проекции на ось Ох действующих на груз сил с учетом закона Гука получаем

или

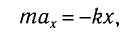
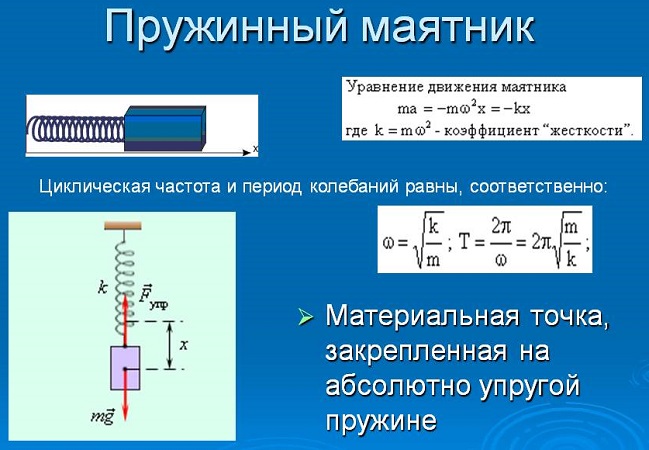
Это уравнение аналогично уравнению гармонических колебаний

Сравнивая эти два уравнения, находим циклическую частоту колебаний пружинного маятника:

Тогда период колебаний пружинного маятника можно найти по формуле

Как следует из полученной формулы, период колебаний пружинного маятника не зависит от амплитуды его колебаний (в пределах выполнимости закона Гука).

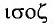
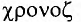
Свойство независимости периода колебаний маятника от амплитуды называется изохронностью (от греческих слов , — равный и — время). Таким образом, колебания пружинного маятника обладают свойством изохронности.

Изохронность колебаний маятника была открыта Галилео Галилеем в 1583 г. при изучении движения грузика, подвешенного на нити. Моделью данной колебательной системы является математический маятник.

Математическим маятником называется материальная точка массой т, подвешенная на невесомой нерастяжимой нити длиной l в поле каких-либо сил, например силы тяжести Земли (рис. 4).

Математический маятник — это идеализированная модель реального маятника при условии, что длина нити намного больше размеров подвешенного на ней тела и масса нити намного меньше массы тела. Кроме того, деформацией нити можно пренебречь.

Галилео Галилей экспериментально определил, что период малых колебаний (9

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Урок 92 (осн). Колебательное движение. МаятникиСкачать

Пружинный маятник — формулы и уравнения нахождения величин

Пружинный маятник — колебательная система, которая состоит из тела, подвешенного к пружине. Эта система способна к совершению свободных колебаний.

Подобные системы довольно широко распространены за счет своей функциональной гибкости. Механизмы на основе таких маятников часто используются как элементы средств автоматики.

В том числе они нашли применение в контактных взрывателях различных боеприпасов, в качестве акселерометров в контурах управления ракет. Так же они активно используются в предохранительных клапанах, устанавливаемых в трубопроводах.

Видео:Колебания математического и пружинного маятников. 9 класс.Скачать

Что такое пружинный маятник

Пружинным маятником в физике называют систему, совершающую колебательные движения под действием силы упругости.

Приняты следующие обозначения:

k — коэффициент жесткости пружины.

Общий вид маятника:

Особенностями пружинных маятников являются:

Сочетание тела и пружины. Массой пружины обычно в расчетах пренебрегают. Роль тела могут играть различные объекты. На них оказывают действие внешние силы. Груз может крепиться разными способами. Витки пружины, которыми она начинается и заканчивается, изготавливают с учетом повышенной нагрузки;

У любой пружины есть исходное положение, предел сжатия и растяжения. При максимальном сжатии зазора между витками нет. Когда она максимально растянута, возникает необратимая деформация;

Полная механическая энергия появляется с началом процесса обратимого деформирования. В этот момент на объект не оказывает действие сила упругости;

Колебательные движения происходят под влиянием силы упругости. Масштаб влияния определяется несколькими причинами (тип сплава, расположение витков и т. д.). Так как может происходить и сжатие и растяжение, можно сделать вывод, что сила упругости действует в двух противоположных направлениях;

От массы тела, величины и направления прикладываемой силы зависит скорость в плоскости его перемещения. Например, если подвесить груз к пружине и, растянув её, отпустить, то груз будет перемещаться в двух плоскостях: вертикально и горизонтально.

Видео:Колебания математического и пружинного маятников. Практическая часть - решение задачи. 9 класс.Скачать

Виды пружинных маятников

Существует два типа данной системы:

Вертикальный маятник — на тело довольно сильно влияет сила тяжести. Это влияние обуславливает увеличение инерционных движений, которые совершает тело в исходной точке.

Горизонтальный — в таком варианте при движении на груз начинает действовать сила трения, возникающая по причине того, что груз лежит на поверхности.

Видео:Математические и пружинные маятники. 11 класс.Скачать

Сила упругости в пружинном маятнике

До начала деформирования пружина находится в равновесном состоянии. Прикладываемое усилие может как растягивать, так и сжимать её.

Применяя к пружинному маятнику закон сохранения энергии, мы можем рассчитать силу упругости в нем. Упругость прямо пропорциональна расстоянию, на которое сместился груз.

Расчёт силы упругости может быть проведен таким образом:

где k — коэффициент жесткости пружины (Нм),

Видео:Математические и пружинные маятники. Практическая часть- решение задачи. 11 класс.Скачать

Уравнения колебаний пружинного маятника

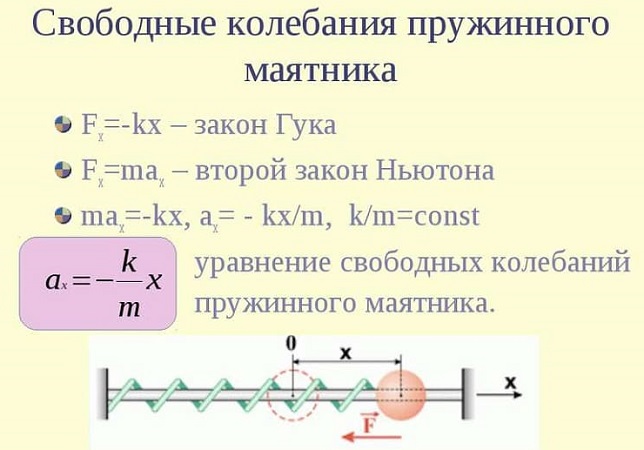
Свободные колебания пружинного маятника описываются с помощью гармонического закона.

Если допустить вероятность того, что колебания идут вдоль оси Х, и при этом выполняется закон Гука, то уравнение примет вид:

F(t) = ma(t) = — mw2x(t),

где w — радиальная частота гармонического колебания.

Для проведения расчета колебаний, учитывая все вероятности, применяют следующие формулы:

Видео:Видеоурок по физике "Математический и пружинный маятники"Скачать

Период и частота свободных колебаний пружинного маятника

При разработке проектов всегда определяется период колебаний и их частота. Для их измерения используются известные в физике формулы.

Изменение циклической частоты покажет формула, приведенная на рисунке:

Факторы, от которых зависит частота:

Коэффициент упругости. На этот коэффициент влияет количество витков, их диаметр, расстояние между ними, длина пружины, жесткость используемого сплава и т. д.

Масса груза. От этого фактора зависит возникающая инерция и скорость перемещения.

Видео:Период колебаний пружинного маятникаСкачать

Амплитуда и начальная фаза пружинного маятника

Учитывая начальные условия и рассчитав уравнение колебаний, можем точно описать колебания пружинного маятника.

В качестве начальных условий используются: амплитуда (А) и начальная фаза колебаний (ϕ).

Видео:Физика 9 класс (Урок№11 - Гармонические колебания. Затухающие колебания. Резонанс.)Скачать

Энергия пружинного маятника

При рассмотрении колебания тел учитывают, что груз движется прямолинейно. Полная механическая энергия тела в каждой точке траектории является константой и равняется сумме его потенциальной энергии и кинетической энергии.

Расчет имеет особенности. При его проведении нужно учитывать несколько условий:

Колебания проходят в двух плоскостях: вертикальной и горизонтальной.

В качестве равновесного положения выбирается ноль потенциальной энергии. Находясь в этом положении пружина сохраняет свою форму.

Влияние силы трения при расчете не учитывают.

Видео:Уравнения и графики механических гармонических колебаний. Практ. часть - решение задачи. 11 класс.Скачать

Дифференциальное уравнение гармонических колебаний пружинного маятника

Отметим, что пружинный маятник — это обобщенное определение. Скорость движения груза (тела) напрямую зависит от комплекса условий, в том числе приложенного к нему усилия.

Видео:5.2 Пружинный маятникСкачать

Формулы пружинного маятника

Видео:5.4 Уравнение гармонических колебанийСкачать

Определение и формулы пружинного маятника

Пружинным маятником называют систему, которая состоит из упругой пружины, к которой прикреплен груз.

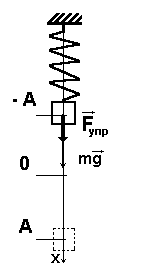
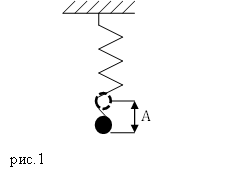
Допустим, что масса груза равна $m$, коэффициент упругости пружины $k$. Масса пружины в таком маятнике обычно не учитывается. Если рассматривать вертикальные движения груза (рис.1), то он движется под действием силы тяжести и силы упругости, если систему вывели из состояния равновесия и предоставили самой себе.

Видео:Физика 10 класс. Пружинно механический маятник Решение задачСкачать

Уравнения колебаний пружинного маятника

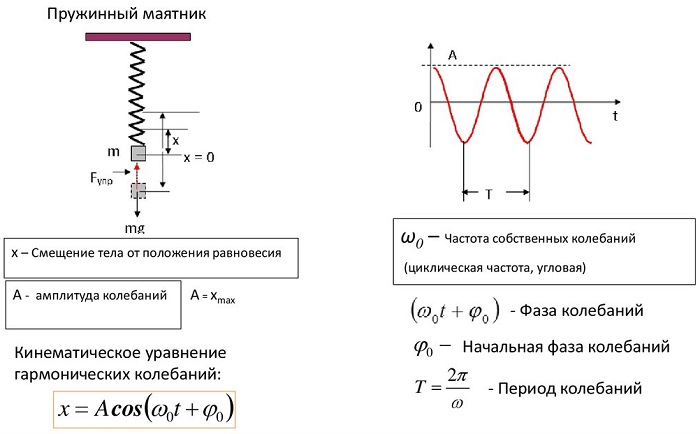
Пружинный маятник, совершающий свободные колебания является примером гармонического осциллятора. Допустим, что маятник совершает колебания вдоль оси X. Если колебания малые, выполняется закон Гука, то уравнение движения груза имеет вид:

где $^2_0=frac$ — циклическая частота колебаний пружинного маятника. Решением уравнения (1) является функция:

где $_0=sqrt<frac>>0$- циклическая частота колебаний маятника, $A$ — амплитуда колебаний; $_0t+varphi )$ — фаза колебаний; $varphi $ и $_1$ — начальные фазы колебаний.

В экспоненциальном виде колебания пружинного маятника можно записать как:

[Re tilde=Releft(Acdot exp left(ileft(_0t+varphi right)right)right)left(3right).]

Видео:9 класс, 34 урок, Колебания математического маятника и груза на пружинеСкачать

Формулы периода и частоты колебаний пружинного маятника

Если в упругих колебаниях выполняется закон Гука, то период колебаний пружинного маятника вычисляют при помощи формулы:

Так как частота колебаний ($nu $) — величина обратная к периоду, то:

Видео:Механика. Л 10.1. Колебания. Вывод дифференциального уравнения пружинного маятникаСкачать

Формулы амплитуды и начальной фазы пружинного маятника

Зная уравнение колебаний пружинного маятника (1 или 2) и начальные условия можно полностью описать гармонические колебания пружинного маятника. Начальные условия определяют амплитуда ($A$) и начальная фаза колебаний ($varphi $).

Амплитуду можно найти как:

начальная фаза при этом:

где $v_0$ — скорость груза при $t=0 c$, когда координата груза равна $x_0$.

Видео:Физика 9 класс (Урок№10 - Маятник. Характеристики колебательного движения.)Скачать

Энергия колебаний пружинного маятника

При одномерном движении пружинного маятника между двумя точками его движения существует только один путь, следовательно, выполняется условие потенциальности силы (любую силу можно считать потенциальной, если она зависит только от координат). Так как силы, действующие на пружинный маятник потенциальны, то можно говорить о потенциальной энергии.

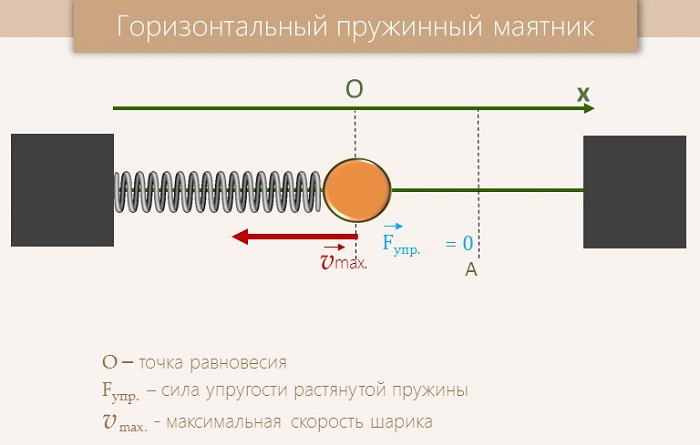
Пусть пружинный маятник совершает колебания в горизонтальной плоскости (рис.2). За ноль потенциальной энергии маятника примем положение его равновесия, где поместим начало координат. Силы трения не учитываем. Используя формулу, связывающую потенциальную силу и потенциальную энергию для одномерного случая:

учитывая, что для пружинного маятника $F=-kx$,

тогда потенциальная энергия ($E_p$) пружинного маятника равна:

Закон сохранения энергии для пружинного маятника запишем как:

где $dot=v$ — скорость движения груза; $E_k=frac<m<dot>^2>$ — кинетическая энергия маятника.

Из формулы (10) можно сделать следующие выводы:

• Максимальная кинетическая энергия маятника равна его максимальной потенциальной энергии.
• Средняя кинетическая энергия по времени осциллятора равна его средней по времени потенциальной энергии.

Видео:Урок 343. Затухающие колебания (часть 1)Скачать

Примеры задач с решением

Задание. Маленький шарик, массой $m=0,36$ кг прикреплен к горизонтальной пружине, коэффициент упругости которой равен $k=1600 frac$. Каково было начальное смещение шарика от положения равновесия ($x_0$), если он при колебаниях проходит его со скоростью $v=1 frac$?

Решение. Сделаем рисунок.

По закону сохранения механической энергии (так как считаем, что сил трения нет), запишем:

где $E_$ — потенциальная энергия шарика при его максимальном смещении от положения равновесия; $E_$ — кинетическая энергия шарика, в момент прохождения положения равновесия.

Потенциальная энергия равна:

В соответствии с (1.1) приравняем правые части (1.2) и (1.3), имеем:

Из (1.4) выразим искомую величину:

Вычислим начальное (максимальное) смещение груза от положения равновесия:

Ответ. $x_0=1,5$ мм

Задание. Пружинный маятник совершает колебания по закону: $x=A $где $A$ и $omega $ — постоянные величины. Когда возвращающая сила в первый раз достигает величины $F_0,$ потенциальная энергия груза равна $E_$. В какой момент времени это произойдет?

Решение. Возвращающей силой для пружинного маятника является сила упругости, равная:

Потенциальную энергию колебаний груза найдем как:

В момент времени, который следует найти $F=F_0$; $E_p=E_$, значит:

📸 Видео

Гармонические колебанияСкачать

Колебания пружинного маятникаСкачать