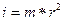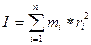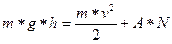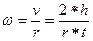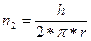Лабораторная работа №9
Изучение основного закона динамики вращательного движения твердого тела
Изучение основного закона вращательного движения твердого тела на приборе Обербека
Приборы и принадлежности:маятник Обербека, вертикальный масштаб, набор грузов, секундомер, штангенциркуль.
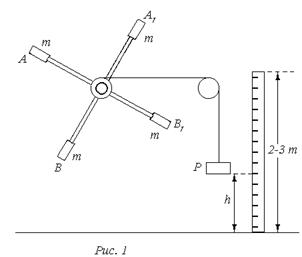
Маятник Обербека, применяемый в настоящей работе, представляет собой маховик крестообразной формы (см. рис. 1). На каждом из четырех стержней помещены одинаковые массы, которые можно перемещать для изменения момента инерции системы.
На оси прибора имеется валик, (шкив), на который наматывается нить. Если к нити подвесить груз, то, разматываясь под действием груза, она приведет весь маховик в равноускоренное вращательное движение.
Краткая теория и цель работы.
Основной закон вращательного движения твердого тела гласит: УГЛОВОЕ УСКОРЕНИЕ ПРЯМО ПРОПОРЦИОНАЛЬНО МОМЕНТУ СИЛЫ И ОБРАТНО ПРОПОРИОНАЛЬНО МОМЕНТУ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ОСИ ВРАЩЕНИЯ.
Если обозначить угловое ускорение через e, то
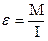
Выражение (1) играет для вращательного движения такую же роль как второй закон Ньютона для поступательного движения.
При этом момент силы для вращательного движения является аналогом силы для поступательного движения, а момент инерции — аналогом массы, т.е. является мерой инертности тела при вращательном движении.
Проверка соотношения (1) и является целью настоящей работы.
Выполнение работы
1 В первой части работы необходимо проверить то, что при постоянном моменте инерции величина углового ускорения прямо пропорциональна моменту силы. Для этого при снятых со стержней грузах подвешивают к нити груз известной массы m1 (масса одного груза 50 г.) и, заметив по вертикальному масштабу положение груза, представляют ему возможность двигаться вниз. Если время падения груза равно t1, а высота h, то ускорение движения груза
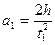
C таким же тангенциальным ускорением движутся точки на поверхности валика. Если радиус валика r, то угловое ускорение
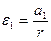
Подвесим теперь к нити груз m2 и, повторив с ним те же опыты, найдем
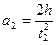
где t2 – время падения второго груза, и
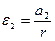
Проделав с каждым грузом опыт 3-5 раз, находят среднее значение e1 и e2 и отношение e1:e2.
Момент силы в обоих случаях находят следующим образом: силой, создающей вращающий момент, является сила натяжения нити ¦, направленная по касательной к валику и момент силы для первого случая может быть записан
Уравнение движения опускающегося груза имеет вид:
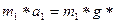
следовательно, ¦ = m1* (g – a1) * r и вращающий момент в 1-ом случае равен:
Составив отношение М1:М2 , сравнивают его с отношением e1:e2.
Должно иметь место:
Примечание: так как в обоих опытах a
1. Сформулировать основной закон вращательного движения и раскрыть содержание понятия “момент силы”. Как создается вращающий момент в приборе Обербека? Чему он равен?
2. Какая связь между угловым ускорение маятника и ускорением, с которым опускается груз?
3. Какая теория лежит в основе инерции системы, если на стержни помещены дополнительные цилиндрические грузы? Поясните происхождение каждого члена правой части равенства (10). Вывести формулу (10).
4. Понятие момента инерции точки, тела?
Определение момента инерции махового колеса.
Приборы и принадлежности: Маховое колесо, платформа с грузами и нитью, секундомер, штангенциркуль, масштабная линейка.
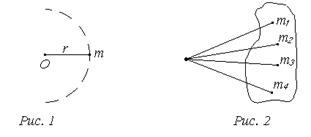
Моментом инерции материальной точки относительно какой-либо оси вращения называется произведение массы точки на квадрат расстояния ее до оси вращения (см. рис. 1).
Момент инерции материальной точки может быть выражен формулой
i – момент инерции материальной точки, m – масса, r – расстояние от точки до оси вращения, проходящей через точку “O”.
Тело можно представить как совокупность материальных точек. Момент инерции тела относительно какой-либо оси вращения равен сумме моментов инерции тела относительно той же оси всех материальных точек, составляющих тело (см. рис. 2), т.е.
где I – момент инерции тела, mi – масса точки, ri — расстояние i-й точки до оси вращения.
Если тело имеет правильную геометрическую форму, то его момент инерции может быть вычислен на основе теоретических соображений.
 |
Если же тело представляет собой сложную фигуру (маховое колесо, пропеллер и т.д.),
То теоретическое определение момента инерции представляет значительные трудности; в этих случаях он определяется опытным путем.
Один из методов опытного определения момента инерции тела (махового колеса) и рассматривается в данной работе.
Описание установки и методики работы.
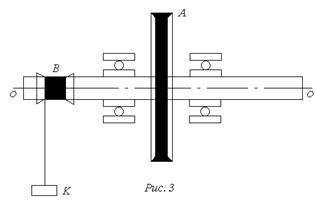
Установка для опытного определения момента инерции махового колеса представляет собой вал “OO”, вращающийся на шариковых подшипниках (см. рис. 3).
На вал насажен шкив “B” и маховое колесо “A”. На поверхность шкива “B” наматывается нить, к концу которой прикреплен груз “К”, масса которого равна “m”,
 |
Поднятый на высоту “h” груз обладает потенциальной энергией Wn=m*g*h,
где g – ускорение свободного падения тела. Если поднятому на высоту “h” грузу дать возможность падать, то создается постоянный вращающий момент, под действием которого колесо будет равномерно-ускоренно вращаться. По мере падения груза его потенциальная энергия будет уменьшаться, превращаясь в эквивалентное количество других видов энергии, а именно: вкинетическую энергию поступательного движения самого груза, равную
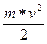
где m – масса груза, v – его скорость движения, и в кинетическую энергию вращательного движения маховика, равную
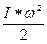
где I – момент инерции маховика, w — его угловая скорость, и в работу по преодолению трения при одном обороте махового колеса, n1 – число оборотов вала (махового) колеса при падении груза от верхней точки до пола.
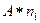
A – работа силы трения при одном обороте.
В тот момент, когда груз “K” достигнет пола, вся его потенциальная энергия m*g*h , которой он обладает в верхней точке, целиком перейдет в энергию поступательного движения падающего груза (1), в кинетическую энергию вращающегося маховика (2) и работу по преодолению трения (3).
В этом случае, на основании закона сохранения энергии можно записать:
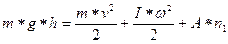
Работа (А) по преодолению трения при одном обороте может быть подсчитана следующим образом:
В тот момент, когда груз достигнет пола, нить, к которой прикреплен он, спадает со шкива, и маховое колесо некоторое время продолжает вращаться, пока его кинетическая энергия не будет израсходована на работу по преодолению трения, т.е.
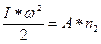
где А – работа по преодолению трения при одном обороте колеса, n2 – число оборотов колеса с момента прекращения действия груза до полной остановки махового колеса.
Тогда формула (4) примет вид
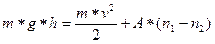
где 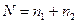
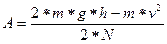
Величина скорости груза v , в тот момент, когда он достигнет пола, равна:
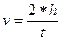
Число оборотов от начала движения до удара груза о пол
h – высоту его подвеса,
N – число оборотов от начала движения до полной остановки маховика,
r – радиус шкива,
n1 – число оборотов от начала движения до удара груза о пол,
t – время движения груза,
v – скорость груза в момент удара о пол,
w — угловую скорость маховика в момент удара груза,
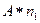
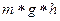
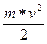
по формуле (4) можно рассчитать I – момент инерции махового колеса. Вес грузов – 1,5 кг
Порядок выполнения работы
1. Измерить при помощи штангенциркуля радиус шкива.
2. Намотать на шкив тонкий шнур, на одном конце которого имеется петля для груза. Вращать маховик до тех пор, пока груз не поднимется на высоту приблизительно 1,5 метра.
3. Измерить расстояние от пола до нижней поверхности груза, установленного в исходное положение.
4. Дав грузу возможность падать, определить с помощью секундомера время падения груза до пола. Для этого следует с началом движения пустить в ход секундомер и остановить его в момент удара о пол. Одновременно следует вести счет числа оборотов маховика с начала движения доудара груза о пол и до полной остановки маховика, секундомер пускается в ход началом движения со счетом нуль. Опыт проделать 5 раз, беря одну и туже высоту подъема груза, для расчетов взять среднее арифметическое оборотов.
5. Все измеренные величины записать в таблицу 1.
6. Произвести расчеты: n1 – числа оборотов от начала движения до удара груза о пол,
v – скорость груза в момент удара о пол,
w — угловой скорости в момент удара о пол,
А – работы по преодолению трения при одном обороте
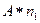
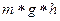
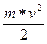
I – момент инерции махового колеса.
Расчеты следует вести в системе “СИ”. Все вычисленные значения занести в таблицу 2, указав размерности вычисленных величин.
Таблица 1
| № налюдения | m | r | N | h | t | v |
| Шкив 1 | ||||||
| Шкив 2 |
Таблица 2
| n1 | 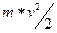 | w | 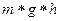 | A | 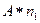 | I |
| Шкив 1 | ||||||
| Шкив 2 |
Примечание: Расчеты величин 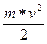
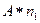
1. Рассмотреть закон сохранения энергии применительно к маховому колесу.
2. Вывести и проанализировать формулу для момента инерции махового колеса.
Видео:Момент инерцииСкачать

Метод измерения и описание аппаратуры
В работе определяется момент инерции махового колеса К, ось симметрии которого параллельна поверхности земли. Колесо находится в состоянии безразличного равновесия, но после крепления к нему добавочного груза Г (рис. 6.2), колесо может колебаться относительно горизонтальной оси.

Если пренебречь силами трения в подшипниках системы, то при малой амплитуде j0 колебаний (j0
cosj0 = 1 — 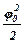
Подставив это значение косинуса в левую часть уравнения (8), получим формулу для расчета Iобщ относительно оси О:
Iобщ = 
Момент инерции добавочного груза IГ находим по теореме Штейнера. В лабораторной установке добавочный груз выполнен в виде диска из однородного материала и укреплен так, что его геометрическая ось параллельна оси симметрии махового колеса. Момент инерции добавочного груза Г относительно оси О (см. рис. 6.3) равен
IГ = 
Первый член правой части равенства — момент инерции груза относительно оси О’, проходящей через его центр масс параллельно оси О. Второе слагаемое – это произведение массы диска на квадрат расстояния между осями О и О’.
Из выражений (10) и (11) получаем, что момент инерции махового колеса
I = Iобщ — IГ = 

Таким образом, определение момента инерции махового колеса в данной работе удалось свести к измерению массы добавочного груза т, радиусов махового колеса R и добавочного груза r, а также – периода колебаний махового колеса Т.
Для того, чтобы подтвердить утверждение о высокой точности данного метода измерения момента инерции, предлагается сравнить полученное значение I с теоретическим (IТ), которое для махового колеса – однородного диска можно вычислить по формуле:
IТ= 
где m0 — масса махового колеса.
Учитывая, что маховое колесо и добавочный груз — диски одинаковой толщины, изготовленные из одного и того же материала (заметим, что для самого метода измерения момента инерции эти факторы несущественны), можно получить равенствоm0 /m =R 2 /r 2 .
Таким образом, массы дисков относятся, как их объемы или (при одинаковой толщине) – как квадраты их радиусов. Выразив из последнего уравнения массу m0 и подставив её в формулу (13), получим
IТ= 
В настоящей работе непосредственно измеряются диаметры махового колеса D и добавочного груза d, а также — время tдесяти полных колебаний. Масса груза m и ускорение свободного падения считаются заданными с известной степенью точности. Используя эти обозначения, окончательно запишем:
I = 
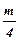

IТ= 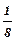
Порядок выполнения работы
Часть 1. Проведение измерений
1. Ознакомьтесь с измерительными приборами, используемыми в данной работе: штангенциркулем и секундомером. Определите значения приборной погрешности штангенциркуля (Dx) и секундомера (Dt); результаты запишите в таблицу 1.
2. Ознакомьтесь с установкой, на которой будете выполнять лабораторную работу. Значение массы добавочного груза m запишите в таблицу 1.
| Приборные погрешности | Масса добавочного груза m, кг |
| штангенциркуля Dx, м | секундомера Dt, с |
Измерьте штангенциркулем диаметры махового колеса и добавочного груза с точностью, которую обеспечивает штангенциркуль. Результаты измерений занесите в таблицу 2.
| Номер измерения | Средние значения |
| Диаметр махового колеса D, м | Dср = |
| Диаметр добавочного груза d, м | dср = |
| Время десяти полных колебаний t, с | tср = |
| Период колебаний T, с | Tср = |
| Момент инерции махового колеса I, кг×м 2 | Iср = IТ = |
4. Отклонив колесо с добавочным грузом на малый угол, удовлетворяющий соотношению (9), отсчитайте время tдесяти полных колебаний. Результаты измерений занесите в таблицу 2.
5. Повторите измерения по пп. 3 — 4 пять раз. Результаты измерений занесите в таблицу 2.
Часть 2. Обработка результатов измерений
Внимание! При проведении вычислений по пунктам 6 — 8 сохраняйте несколько значащих цифр после запятой. Округление итогового выражения для момента инерции махового колеса проводится только после вычисления ошибки измерений (см. пункт 9).
6. Вычислите значения периода колебаний махового колеса для всех пяти случаев.
7. Вычислите средние значения диаметров и махового колеса Dcp и dсрдобавочного груза, периода колебаний Тср, а затем, используя эти данные и формулу (15), рассчитайте, чему равно среднее значение момента инерции махового колеса Iср. В вычислениях принять g= 9,81 м/с 2 .
8. Используя полученные значения Dcp и dср, а такжезначение массы добавочного груза m, по формуле (16)рассчитайте теоретическое значение момента инерции махового колеса IТ.
Результаты расчетов по пп. 6 — 8 занесите в таблицу 2.
9. Поскольку в эксперименте непосредственно измеряются лишь D, d и t, а величина момента инерции определяется косвенным образом из расчетов по формуле (15), для вычисления ошибки измерения I необходимо пользоваться формулами для расчета ошибок косвенных измерений. Окончательный результат должен быть записан в виде
где DI — абсолютная ошибка измерения момента инерции махового колеса.
В данной работе основную роль в возникновении ошибки определения момента инерции играет случайная ошибка измерения периода колебаний; случайными же погрешностями измерения диаметров махового колеса и добавочного груза, а также — приборными ошибками штангенциркуля и секундомера можно пренебречь. В этом случае ошибка измерения момента инерции махового колеса вычисляется, как среднеквадратичная ошибка:
(DI) 2 = 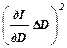



(Подробнее о методах расчета ошибок измерения физических величин см. методические указания [3] из списка рекомендуемой литературы).
Используя формулу (15), получим, что
DI » 

Таким образом, вычисление DI в данной работе сводится к определению случайной ошибки измерения периода колебаний DT:
DT = a 
где a -коэффициент Стьюдента, значения которого можно найти в таблице, имеющейся в лаборатории (таблица приведена также в методических указаниях [3]). Величину доверительной вероятности при выборе коэффициента Стьюдента по этой таблице примите равной 0,95.
10. Результат вычислений DI округлите до первой значащей цифры, после чего округлите полученные ранее (см. таблицу 2) значения Iср и IТ до того же разряда, что и DI.
Запишите окончательный численный результат в виде
Обратите внимание на правильность записи единиц измерения, в которых выражены полученные значения момента инерции махового колеса.
1. Какое свойство тела выражает момент инерции и как он вычисляется для материальной точки и системы материальных точек? В каких единицах он измеряется в СИ?
2. Сформулируйте теорему Штейнера. Как она используется в данной работе?
3. Объясните, из каких соображений в данной работе выбирается число значащих цифр после запятой при округлении результатов вычислений.
5. В чём заключается физический принцип определения момента инерции методом колебаний?
4. Выведите формулы (12) и (14); укажите возможные причины некоторого несовпадения величин моментов инерции, определенных по этим формулам.
1. Савельев И.В. Курс общей физики: В 3-х т. – М.: Наука, 1987. – Т. 1, 432 с.
2. Яворский Б.М., Детлаф А.А. Курс физики. – М.: Высш. шк., 1989.
3. Расчет погрешностей в лабораторных работах физического практикума. Методические указания к вводным занятиям в физическом практикуме/ Н.А.Гринчар, Ф.П.Денисов, Б.А.Курбатов и др.; Под общ. ред. Ф.П.Денисова. — М.: МИИТ, 1995. – 38 с.
Видео:Зависимость углового ускорения от момента инерцииСкачать

Лабораторная работа №6
Видео:Лабораторная работа №2. Определение момента инерции махового колесаСкачать

ОПРЕДЕЛЕНИЕ момента инерции системы: маховое колесо – ось – вал динамическим методом
Фамилия И.О. _________________ Группа __________ Дата ______
Введение
В динамике вращательного движения твердого тела понятия “сила” и “масса” заменяются понятиями “момент силы” и “момент инерции”.
При вращении твердого тела вокруг некоторой оси эффект действия силы зависит не только от величины силы, но и от расстояния точки приложения силы до оси вращения. Поэтому вместо силы вводится момент силы, равный произведению величины действующей силы на плечо (кратчайшее расстояние от оси вращения до направления действующей силы)
Роль массы играет момент инерции. Свойство инертности во вращательном движении зависит не только от массы материальной точки, но и от расстояния этой точки до оси вращения.
Моментом инерции материальной точки называют произведение массы материальной точки на квадрат расстояния ее от оси вращения:

где m – масса материальной точки; r – расстояние материальной точки до оси вращения.
Так как тело состоит из множества точек и при вращении тела около некоторой оси каждая точка обладает некоторым моментом инерции относительно этой оси, то моментом инерции тела относительно этой оси вращения называют сумму моментов инерции всех материальных точек тела:
В этой работе ставится задача определения момента инерции системы, состоящей из махового колеса оси и вала.
Небольшое маховое колесо, которое может вращаться с очень малым трением около горизонтальной оси, расположено на высоте h 0 от пола. Ось вращения проходит через центр тяжести махового колеса. На оси колеса находится небольшого диаметра вал, на который наматывается шнур (рис. 15).
Если к шнуру подвесить гирю массой m 0, и закрутить вал так, чтобы гиря поднялась на высоту g , то гиря и вся система маховое колесо – ось – вал приобретут потенциальную энергию:

где m – масса гири , g – ускорение свободного падения 
Если отпустить гирю, то она начнет падать, раскручивая шнур и вращая всю систему.
Потенциальная энергия гири будет превращаться в кинетическую энергию падающей гири и вращающейся системы маховое колесо – ось – вал

Следовательно, пренебрегая трением, по закону сохранения энергии можно записать:

где 


Считая движение гири равноускоренным, можно написать:
где а – ускорение падения гири: t – вре6мя падения.
Следовательно, определив 

Линейная скорость вращения точки на внешней поверхности вала равна скорости падения гири. Связь между линейной и угловой скоростями вращения:

где r – радиус вала и 





I . Приборы и установка
В нашей лаборатории установка система маховое колесо – ось – вал смонтирована на кронштейне, который укреплен на стене (рис.15).
Шнур укреплен на валу. Установка имеет тормоз, с помощью которого гиря освобождается для падения.
При установке имеется 2 гири разных масс, метровая линейка или рулетка, секундомер и штангенциркуль.
II , Порядок выполнения работы
1. Измерить метровой линейкой или рулеткой с точностью до 1 см высоту поднятия гири от пола до нижней поверхности гири. Штангенциркулем измерить диаметр вала. Эти данные записать.

2. Снять гирю и взвесить на технико-химических весах с точностью до 0,5 г.
3. Повесить гирю на шнур и освободить маховое колесо от тормоза. В этот момент включить секундомер.
4. Гиря начнет падать, раскручивая вал и маховое колесо. В момент удара гири о пол выключить секундомер. Время падения записать.
5. Закручивая маховое колесо, поднять гирю на прежнюю высоту и повторить опыт, как сказано в пунктах 3-м и 4-м еще два-три раза.
Среднее арифметическое значение времени из этих измерений войдет в расчетную формулу (34).
6. Повторить опыт с другой гирей и сделать те же расчеты.
Подсчитать момент инерции системы маховое колесо – ось – вал по формуле (34).
Среднее арифметическое значение момента инерции из всех измерений принимается за значение момента инерции системы маховое колесо – ось – вал.
7. Вычислить относительную и абсолютную ошибки измерений.
🎦 Видео
Лекция 06 Динамика твердого телаСкачать

Урок 94. Вычисление моментов инерции телСкачать

Основное уравнение динамики вращательного движения. 10 класс.Скачать

Урок 93. Основное уравнение динамики вращательного движенияСкачать

Вращательное движение. 10 класс.Скачать

Поступательное и вращательное движенияСкачать

Мгновенный центр вращенияСкачать

Момент силыСкачать

Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

ИЗУЧЕНИЕ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛАСкачать

Грузы на пружинах.Скачать

Лабораторная работа "Определение момента инерции махового колеса методом свободных колебаний"Скачать

Момент инерции абсолютно твердого тела. 10 класс.Скачать

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать

#1 определение момента инерции кольца методом колебанийСкачать

Вращательное движение твёрдого тела. Задачи 1, 2, 3Скачать

МОМЕНТ ИНЕРЦИИ ТВЕРДОГО ТЕЛАСкачать