Уравнение движения маховика с моментом инерции

Цель работы: определить момент инерции маховика.

Законы вращательного движения твердого тела вокруг неподвижной оси

Вращательное движение материальной точки характеризуется следующими величинами: углом поворота, угловой скоростью и угловым ускорением .

При вращательном движении результат действия сил на тело определяется действующим на него моментом силы М и зависит от момента инерции J тела. Произведение момента инерции тела на его угловое ускорение численно равно результирующему моменту сил, действующих на это тело :

Cоотношение (1) называется основным уравнением динамики вращательного движения.

Моментом силы относительно оси называется вектор, направленный вдоль оси, численно равный произведению силы на плечо, если сила действует в плоскости, перпендикулярной оси вращения.

Моментом инерции J материальной точки относительно оси вращения называется произведение массы m точки на квадрат расстояния r до оси вращения

Момент инерции любого тела равен сумме моментов инерции составляющих его материальных точек

J= , (3)

где N — число частиц, на которое разбито тело; mi и ri — масса и расстояние от точки до оси вращения.

Момент инерции тел во воащательном движении выполняет роль, аналогичную роли массы в поступательном движении. Как масса, так и момент инерции являются мерой инертности .

Для однородных тел простой формы момент инерции относительно оси симметрии может быть рассчитан аналитически. Например, момент инерции плоского диска или сплошного цилиндра относительно геометрической оси симметрии равен

J= ,

где m — масса диска или цилиндра, r — радиус диска или цилиндра.

Момент инерции шара относительно оси, совпадающей с любым из его диаметров, вычисляется так:

J= ,

где m и r — масса и радиус шара.

Момент инерции тела относительно любой оси может быть рассчитан по теореме Штейнера, которая формулируется следующим образом : момент инерции J тела относительно произвольной оси равен сумме момента инерции J0 этого тела относительно оси, проходящей через центр тяжести параллельно данной оси, и произведения массы тела m на квадрат расстояния d между осями :

Кинетическая энергия вращающегося относительно неподвижой оси тела также зависит от момента инерции его :

Wкин= . (5)

Работа при вращении твердого тела равна

А=М ,(6)

где М — вращающий момент силы, — угол поворота под действием момента М.

Когда во время движения тела момент инерции его изменяется, основное уравнение динамики вращательного движения должно быть записано в более общей форме:

. (7)

Величина J называется моментом количества движения. Из уравнения (7) как следствие вытекает закон сохранения момента количества движения. Если суммарный момент, действующий на тело или систему тел, равен нулю, то момент количества движения этого тела или системы тел остается неизменным, т.е. если М=0, то L= const.

При сложной геометрической форме тела аналитический подсчет его момента инерции провести трудно. В этих случаях его определяют экспериментально.

Прибор (рис.1) состоит из маховика А, насаженного на вал. Вал установлен на шарикоподшипниках С1 и С2. На этом же валу имеется шкив В с радиусом r. На шкив намотана нить с грузом известной массы m. Вращая маховик, груз поднимают над полом на высоту h, вследствие чего он приобретает потенциальную энергию mgh (g-ускорение силы тяжести). Если груз будет падать, то потенциальная энергия mgh перейдет в кинетическую энергию поступательного движения груза , кинетическую энергию вращательного движения маховика , а также пойдет на работу А=kn1 по преодолению силы трения в опорах. Здесь введены следующие обознначения: m-масса груза; V-его скорость; J-момент инерции маховика; n1-полное число оборотов маховика при падении груза с высоты h; k-постоянный коэффициент, численно равный работе по преодолению трения при одном обороте.

По закону сохранения энергии в момент достижения падающим грузом пола имеем

mgh= + . (8)

Вычислим неизвестный коэффициент k. В момент достижения грузом пола прекращается действие вращающего момента, но колесо продолжает вращаться, пока его кинетическая энергия не израсходуется на работу трения. Допустим, что с момента прекращения действия груза до остановки маховик сделает n2 оборотов. Работа по преодолению трения определяется как и в первом случае:

kn2= , отсюда k= ,

Подставив выражение для k в уравнение (8), получим

mgh= (9)

Движение груза равноускоренное без начальной скорости. Поэтому

h= и V=at= , (10)

где t- время падения груза с высоты h , a- ускорение падения груза.
Найдем угловую скорость маховика по формуле:

. (11)

С учетом выражений(10) и (11) формула (9) принимает вид

mgh= . (12)

Решая это уравнение относительно J, получим

J= . (13)

Порядок выполнения работы

2. Запустить программу 2К.ЕХЕ. Для этого указать курсором на 2К.ЕХЕ и щелкнуть левой кнопкой мыши (в дальнейшем эту команду обозначим L’ на 2К.ЕХЕ). Изучить информацию на экране.

3.L’ на команде «Обновить» Установить значения радиуса шкива r и высоты падения груза h.

4.Задать значение массы m.

5. .L’ на Подготовить.

6. .L’ на Старт. Ждать до прекращения вращения шкива. При этом полученные значения t, n1 и n2 заносятся в таб. 1.

7. Задать новое значение массы m и повторить пункты 5 и 6.

8. Задать новое значение массы m и повторить пункты 5 и 6.

9. Задать новое значение массы m и повторить пункты 5 и 6.

10. Задать новое значение массы m и повторить пункты 5 и 6.

11.Данные таблицы переписать в тетрадь.

12. Пользуясь формулой (13), вычислить значение J.

13. Вычислить средний момент инерции по формуле:

14. Вычислить абсолютную и относительную ошибки измерений.

15.Закрыть программу 2К.ЕХЕ.

Найдем значения момента инерции

J=

∆1=|7,8342-7,5518|=0,2824 кг . м 2

∆2=|7,8342-7,3252|=0,509 кг . м 2

∆3=|7,8342-8,4337|=0,5995 кг . м 2

∆4=|7,8342-8,6185|=0,7843 кг . м 2

∆5=|7,8342-7,2416|=0,5926 кг . м 2

Ответ можем записать в виде J =(7,8342 0,5536) кг*м 2

Относительная погрешность равна

Вывод: в данной лабораторной работе определили момент инерции маховика. Для этого провели 5 измерений, вычислили средние значения момента инерции и абсолютной погрешности, а также определили относительную погрешность.
Контрольные вопросы и задания.

1. В чем заключается физический смысл момента инерции тела?

Момент инерции равен сумме масс элементарных частиц, помноженных на квадрат расстояния до оси вращения.

т. е он зависит от массы в каждой точке тела и от расположения оси вращения

Момент инерции — скалярная величина, характеризующая распределение масс в теле.

Момент инерции является мерой инертности тела при вращении (физический смысл)
2.Как записывается основное уравнение динамики вращательного движения твердого тела?

Когда во время движения тела момент инерции его изменяется, основное уравнение динамики вращательного движения должно быть записано в более общей форме:

Величина J называется моментом количества движения. Из уравнения как следствие вытекает закон сохранения момента количества движения. Если суммарный момент, действующий на тело или систему тел, равен нулю, то момент количества движения этого тела или системы тел остается неизменным, т.е. если М=0, то L= const.

3. Сформулируйте теорему Штейнера.

Момент инерции тела относительно любой оси может быть рассчитан по теореме Штейнера, которая формулируется следующим образом : момент инерции J тела относительно произвольной оси равен сумме момента инерции J ₀ этого тела относительно оси, проходящей через центр тяжести параллельно данной оси, и произведения массы тела m на квадрат расстояния d между осями :

4. Выведите расчетную формулу для момента инерции маховика.

По закону сохранения энергии в момент достижения падающим грузом пола имеем

mgh= + .

Вычислим неизвестный коэффициент k. В момент достижения грузом пола прекращается действие вращающего момента, но колесо продолжает вращаться, пока его кинетическая энергия не израсходуется на работу трения. Допустим, что с момента прекращения действия груза до остановки маховик сделает n ₂ оборотов. Работа по преодолению трения определяется как и в первом случае:

kn2= , отсюда k= ,

Подставив выражение для k в уравнение , получим

mgh=

Движение груза равноускоренное без начальной скорости. Поэтому

h= и V=at,

где t- время падения груза с высоты h , a- ускорение падения груза.

Найдем угловую скорость маховика по формуле:

.

mgh= .

Решая это уравнение относительно J, получим

Видео:Момент инерцииСкачать

Изучение динамики вращательного движения маховика

Лабораторная работа № 16

ИЗУЧЕНИЕ ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ МАХОВИКА

Цель работы – экспериментальное определение момента инерции маховика, состоящего из диска, шкива и вала.

1. Теоретические основы работы

Аналогом второго закона Ньютона, справедливого для описания поступательного движения тела массой m

во вращательном движении является основное уравнение динамики вращательного движения

(2)

где и соответственно момент инерции и угловое ускорение твердого тела относительно неподвижной оси вращения z, – алгебраическая сумма моментов сил относительно оси z.

Сравнительный анализ уравнений (1) и (2) показывает, что роль массы в поступательном движении играет момент инерции тела во вращательном движении. А поскольку масса является мерой инертности тела в поступательном движении, то момент инерции является также мерой инертности тела во вращательном движении. В этом заключается физический смысл момента инерции.

Относительно неподвижной оси z момент инерции твердого тела определяется по формуле

, (3)

где r является кратчайшим расстоянием от элемента тела массой dm до оси z.

Из формулы (3) следует, что момент инерции зависит от массы тела и от ее распределения относительно оси вращения. Чем больше масса тела и чем дальше она находится от оси вращения, тем больше момент инерции твердого тела и наоборот.

Рассмотрим маховик (рис.1), состоящий из диска, шкива и вала. Предположим, что они обладают общей массой М. Диск и шкив насажены на общий вал, закрепленный в подшипниках. Маховик может вращаться относительно оси z, совпадающей с осью вала (на рис.1 ось z перпендикулярна плоскости чертежа и направлена «от нас»).

Рис.1 Схема системы маховик-груз (вал на схеме не показан)

Вращение маховика осуществляется под действием груза массой m1, укрепленного на нити, намотанной на шкив, и описывается относительно неподвижной оси z уравнением

, (4)

где момент инерции маховика, – его угловое ускорение, – сумма моментов сил, действующих на маховик. включает момент силы натяжения нити М(Т2) и момент силы трения М(Fтр) в подшипниках вала. Моменты сил N и Мg относительно оси z равны нулю. Таким образом

. (5)

Поступательное движение груза массой m1 описывается вторым законом Ньютона

, (6)

где а является ускорением центра масс груза, Т1 – силой натяжения нити, приложенной к грузу. В проекции на ось у уравнение (6) принимает вид

(7)

Так как предполагается, что нить нерастяжима и невесома, то ускорение всех точек нити и груза одинаковы, причем в отсутствии проскальзывания нити линейное (тангенциальное) ускорение обода диска равно ускорению груза. Силы натяжения нити Т1 и Т2 равны между собой (Т1 = Т2 = Т).

Предположим, что груз в процессе движения всей системы опускается до некоторого нулевого уровня с высоты h1. Тогда с учетом, что

, (8)

где t – время движения груза, а

; (9)

. (10)

Из уравнения (5) находим

. (11)

Силу натяжения Т выражаем из уравнения (7), а угловое ускорение e – из (10). Затем полученные формулы для Т и e подставляем в (11). В итоге получаем

. (12)

Для расчета нужно знать все величины, входящие в формулу (12). Они определяются экспериментально: – с помощью штангенциркуля, – с помощью линейки, t – с помощью секундомера. Масса груза m1 изначально задана. Момент силы трения определяется опытным путем. Для этого груз еще раз поднимают на первоначальную высоту (одновременно наматывая нить на шкив маховика), а затем предоставляют его самому себе. Груз сначала опускается на h1 до нижней точки – нулевого отсчета высоты (нить при этом сматывается со шкива), а затем (когда нить начинает наматываться на шкив) поднимается на меньшую высоту . Спуск и подъем груза происходят в течение некоторого времени t2 . Причиной подъема груза на меньшую высоту является наличие силы трения в подшипниках вала. Потеря механической энергии системы определяется работой силы трения

. (13)

Так как начальная и конечная кинетические энергии и равны нулю, то изменение механической энергии системы равно изменению только потенциальной энергии груза

. (14)

Работа силы трения выражается через момент силы трения и угловое перемещение маховика Dj :

. (15)

Приравнивая правые части уравнений (14) и (15), имеем

. (16)

Угловое перемещение маховика Dj равно отношению длины дуги, которую опишут за время поворота t2 точки обода шкива, к его радиусу:

Dj . (17)

Подставляя Dj в уравнение (16), имеем

. (18)

И, наконец, подставляя выражения для в уравнение (12), получаем формулу для определения экспериментального значения момента инерции маховика

. (19)

Экспериментально определенное значение Jzэ можно сравнить с теоретическим значением того же момента инерции Jzт, рассчитанного по формуле

.

Так как материал, из которого изготовлен шкив, обладает гораздо меньшей плотностью, чем плотность стальных диска и вала, то моментом инерции шкива Jz шкива можно пренебречь. Сам диск можно представить в виде совокупности двух элементов (см. раздел 2: «описание экспериментальной установки»).

, где

– момент инерции тонкого диска, – момент инерции кольца (здесь М1 и М2 являются соответственно массами тонкого диска и кольца, R1 – внешний радиус тонкого диска и одновременно внутренний радиус кольца, R2 – внешний радиус кольца).

. (20)

Данные установки представлены в разделе 2.

2. Описание экспериментальной установки

Схема экспериментальной установки приведена на рис.2. Основными ее элементами являются: диск 1, шкив 2 и груз 3. Груз подвешен на нити, намотанной на шкив. Диск вместе со шкивом смонтированы на едином соосным с ними валу 4. Вал крепится в подшипниках 5. Для регистрации местоположения груза в установке предусмотрена вертикально расположенная линейка 6. Все элементы установки смонтированы на массивной металлической опоре.

Рис. 2. Схема экспериментальной установки

Диск 1 представляет собой единую конструкцию в виде фигуры вращения. Диск для удобства расчета его момента инерции условно можно разделить на два отдельных элемента: тонкий диск (рис.3) и кольцо (рис.4):

Рис.3. Тонкий диск массой Рис.4. Кольцо массой

(Напоминаем, что моменты инерции этих тел не зависят от их толщины).

1. Заполните табл.1 спецификации измерительных приборов. Внесите в протокол данные установки.

Спецификация измерительных приборов

Название прибора и его тип

Масса груза m1 = Dm1 =

Момент инерции вала Jzвала = 1,36×10–4 кг×м2 DJzвала =

Масса тонкого диска = 2,91 кг D =

Радиус R1 = 162,0 мм DR1 = 0,25 мм

Масса кольца = 9,92 кг DМ2 =

Радиус R2 = 122,5 мм DR2 = 0,25 мм

2. С помощью штангенциркуля измерьте диаметр шкива d, значение диаметра запишите в табл.2. При построении таблицы предусмотрите необходимое для записи измерений число строк.

Измерение времени движения груза t, диаметр шкива d и высот h1 и h2

3. Проверьте, чтобы нижняя торцевая поверхность груза при полностью размотанной нити, к которой он подвешен, находилась на уровне нулевой отметки на шкале линейки (в противном случае за нулевую отметку примите то деление шкалы линейки, которое соответствует положению нижнего торца груза, когда нить полностью размотана).

4. Намотайте нить на шкив таким образом, чтобы нижняя торцевая поверхность груза располагалась напротив отметки на линейке, соответствующей высоте h1 (значение h1 согласуйте с преподавателем).

5. Предоставьте груз самому себе (отпустите), тем самым, заставив маховик вращаться; одновременно включите секундомер.

6. Выключите секундомер в момент достижения грузом нулевой отметки на шкале линейки. Полученное время движения груза t внесите в табл.2. Проделайте эксперимент по измерению диаметра шкива d (п.2) и по измерению времени t (п. п. 4,5,6) еще 4 раза. Всего измерений как d, так и t должно быть пять. Все измеренные значения d и t внесите в табл.2.

7. Поднимите груз на высоту h1 (одновременно наматывая нить на шкив) и вновь предоставьте его самому себе (отпустите). Наблюдая за поступательным движением груза, зафиксируйте максимальную высоту h2, на которую поднимется груз после прохождения им нулевой отметки на шкале линейки. Этот эксперимент повторите еще 4 раза. Значения h2 (всего 5 значений) внесите в табл.2.

4. Обработка результатов измерений

1. Рассчитайте значения радиуса шкива и внесите их в табл.2.

2. Используя данные, приведенные в табл.2, вычислите средние значения времени t, высот h1 и h2, радиуса r. Эти значения внесите в нижнюю строчку табл.2.

3. С учетом средних значений величин t, h1, h2 и r рассчитайте экспериментальное значение момента инерции маховика по формуле (19).

4. Рассчитайте теоретическое значение момента инерции маховика из уравнения (20). (Расчеты должны быть последовательными и должны включать буквенные обозначения величин и их численные значения. Это указание в полной мере относится и к расчетам погрешностей величин. Все расчеты должны быть выполнены в протоколе лабораторной работы).

5. Рассчитайте погрешность экспериментального значения момента инерции маховика по формуле:

6. Рассчитайте погрешность теоретического значения момента инерции маховика по формуле:

.

7. Окончательные результаты для экспериментальных и теоретических значений Jz запишите в стандартном виде

и приведите друг под другом.

5. Контрольные вопросы.

1. Как определяется момент инерции материальной точки, системы материальных точек, твердого тела?

2. От чего зависит момент инерции твердого тела массой m относительно данной оси вращения z?

3. Каков физический смысл момента инерции твердого тела?

4. Дайте определение момента силы относительно полюса и неподвижной оси.

5. Каким образом в работе определяется работа сил трения в подшипниках вала?

6. Получите уравнение для расчета момента инерции маховика, пренебрегая трением в подшипниках вала.

Видео:Зависимость углового ускорения от момента инерцииСкачать

Реферат: Определение момента инерции маховика

Лабораторная работа № 10

Определение момента инерции маховика

Экспериментальное определение момента инерции системы * , состоящей из массивного маховика, двух шкивов, насаженных на общий вал.

Теоретические основы работы

В механике под твердым телом, или абсолютно твердым телом, понимают неизменную систему материальных точек, т. е. такую абстрактную (идеализированную) систему, при любых движениях которой взаимные расстояния между материальными точками остаются неизменными, постоянными.

Любое сложное движение твердого тела можно представить как совокупность простых движений: поступательного и вращательного.

При поступательном движении все точки твердого тела совершают одинаковые перемещения, т. е. в этом случае любая прямая, проведенная в твердом теле, остается при движении параллельной самой себе.

Мерой инертности (инерции) ** твердого тела при поступательном движении является масса тела.

При вращательном движении твердого тела как вокруг неподвижной оси, так и вокруг точки, инертные свойства тела определяются моментом инерции.

Следует подчеркнуть, что тело имеет момент инерции относительно любой оси независимо от того, вращается оно или покоится по аналогии с тем, что любое тело имеет массу независимо от того, движется оно или находится в покое.

В механике различают осевые и центробежные моменты инерции твердого тела, но в курсе общей физики изучается только момент инерции твердого тела относительно оси, что является целью данной лабораторной работы.

Момент инерции твердого тела относительно оси вращения равен сумме произведений элементарных масс тела на квадраты их расстояний до этой оси, т. е.

. (1)

В системе «СИ» момент инерции имеет размерность (кг×м 2 ).

* Так как масса (и размеры) массивного маховика значительно больше суммарной массы шкивов и вала, то фразу «момент инерции системы» следует понимать буквально как момент инерции маховика.

** Свойство тела оказывать сопротивление при попытках вывести его из состояния покоя или изменить его скорость (по модулю или направлению), называется инертностью.

Момент инерции относительно данной оси зависит не только от величины массы тела, но и от распределения масс относительно оси. Изменения расстояний частиц тела относительно оси приводят к различным значениям момента инерции тела относительно этой же оси.

Момент инерции твердого тела, как и масса тела, является величиной аддитивной.

Суммирование в формуле (1) может быть заменено интегрированием:

, (2)

где — плотность тела в точке, в которой взят элементарный объем dV;

r — расстояние объема dV от оси вращения.

Если твердое тело однородно, т. е. во всех его точках плотность r= const, то выражение (2) принимает вид:

. (3)

Вычисление момента инерции реальных твердых тел (произвольной конфигурации) по формулам (2, 3) представляет собой весьма сложную проблему, и на практике моменты инерции этих тел определяют экспериментальным путем.

Что касается однородных осесимметричных тел (цилиндра, конуса, шара и т. д.), то вычисление интеграла (3) значительно упрощается.

Учитывая, что в предлагаемой лабораторной работе вал, маховик, шкивы представляют собой цилиндры (диски), то приведем пример вычисления момента инерции однородного цилиндра (диска) относительно его оси симметрии (геометрической оси) ОО₁ (рис. 30).

Мысленно разобьем цилиндр (диск) радиуса R и высотой h на концентрические слои толщиной dr, радиус которого равен r.

Масса вещества, заключенного в этом слое, равна

, (4)

где — плотность вещества цилиндра.

Момент инерции этого слоя относительно оси вращения ОО₁ равен

. (5)

Согласно (2) или (3) момент инерции всего цилиндра (диска) относительно оси ОО₁ равен

. (6)

Учитывая, что масса всего цилиндра (диска)

,

выражение (6) принимает окончательный вид:

(7)

Итак, момент инерции сплошного однородного цилиндра (диска) относительно оси симметрии равен его массе, умноженной на половину квадрата его радиуса.

Существует ряд методов (метод вращения и метод колебаний) экспериментального определения момента инерции твердого тела произвольной формы или системы, состоящей из нескольких тел, относительно оси вращения.

В данной лабораторной работе предлагается экспериментальное определение момента инерции системы, состоящей из однородных цилиндров (дисков) методом вращения.

Описание экспериментальной установки

На рис. 31 схематически показана лабораторная установка, с помощью которой исследуются закономерности поступательного и вращательного движения тел, необходимые для вычисления момента инерции системы.

Маховик 1 насажен на вал 2, который закреплен в шарикоподшипниках 3, 4, что обеспечивает вращение системы вокруг горизонтальной оси. На этом валу закреплены два шкива большего 5 и меньшего 6 диаметров. Диаметры шкивов измеряются штангенциркулем. На ободе каждого шкива имеется штырь для крепления нити с грузом.

На один из шкивов наматывается невесомая и нерастяжимая нить, к свободному концу которой прикрепляется груз 7 массой m. Положение груза относительно пола, т. е. высота h, измеряется длинной линейкой с миллиметровыми делениями.

Измерение времени движения груза 7 до пола осуществляется секундомером.

Для вывода расчетной формулы момента инерции системы могут быть использованы динамический или энергетический подходы. В данном случае предлагается вывод, основанный на законе сохранения и превращения механической энергии.

Пусть груз массой m (рис. 31) находится в покое на высоте h над горизонтальной поверхностью (на высоте h от пола).

Из кинематики равноускоренного движения материальной точки имеем:

и .

Исключая из последних выражений ускорение a, выразим скорость груза v непосредственно перед ударом его о пол:

, (8)

где t — время движения груза с высоты h.

В отсутствие проскальзывания нити можно использовать известную связь между модулями линейной и угловой скоростей:

, (9)

где r — радиус шкива, на который намотана нить с грузом;

u — линейная скорость точек на ободе этого шкива.

Из (8) и (9) получаем выражение для угловой скорости * (шкива, маховика, всей системы) в момент времени t касания груза массой m о пол:

. (10)

При расчете момента инерции системы необходимо учитывать влияние силы трения в подшипниках крепления вала.

В начальный момент система находится в покое, и груз массой m расположен на высоте h от пола. Следовательно, перед началом движения система обладает энергией, равной потенциальной энергии груза, т. е.

. (11)

Если систему предоставить самой себе, то груз массой m будет равноускоренно опускаться, а маховик со шкивами приходить во вращательное движение.

В момент касания грузом пола потенциальная энергия груза переходит в суммарную кинетическую энергию системы и в работу против силы трения в подшипниках:

, (12)

где — кинетическая энергия груза к моменту достижения пола;

— кинетическая энергия вращательного движения маховика со шкивами к моменту достижения пола грузом;

— работа силы трения за n₁ оборотов (число оборотов маховика от начала движения груза с высоты h до пола).

Уравнение (12) можно представить в виде:

. (13)

*Напомним, что любая точка твердого тела, вращающегося вокруг неподвижной оси, имеет одну и ту же угловую скорость.

**При вращении твердого тела вокруг неподвижной оси с угловой скоростью wi — ая частица тела, отстоящая от оси вращения на расстояние r_i , обладает линейной скоростью
u_i = wr_i (см. формулу (9)). Значит, кинетическая энергия этой частицы равна:

Суммируя последнее выражение, получим кинетическую энергию всего тела:

С учетом (1) получим формулу кинетической энергии твердого тела, вращающегося вокруг неподвижной оси: Е_квр . = Iw 2 /2.

После падения груза на пол и соскальзывания нити со шкива маховик продолжает вращаться до полной остановки. Это означает, что кинетическая энергия вращающегося маховика полностью перешла в работу силы трения, т.е.

, . (14)

где — работа силы трения за n₂ оборотов, т. е. до полной остановки маховика.

Работа силы трения (13) и (14), как неконсервативной (или диссипативной) силы, как правило, отрицательна и в условиях данного эксперимента пропорциональна числу оборотов, совершенных маховиком на первом и втором этапах:

, , (15)

где k — положительный коэффициент, имеющий одно и то же значение в обоих случаях, и который можно представить с учетом (14) в следующем виде:

, . (16)

Тогда (15) с учетом (16) определяется следующим выражением:

. (17)

Уравнение (13) с учетом (17) принимает вид:

.

Преобразуя последнее равенство, получим с учетом (9) и (10) формулу расчета момента инерции системы:

,

которую можно упростить, учитывая, что >>2h и радиус шкива .

Итак, расчетная формула момента инерции системы принимает окончательный вид:

, (18)

где d — диаметр шкива.

Порядок выполнения работы

1. Штангенциркулем измерьте не менее 5 раз диаметр (d) большего шкива 5 (рис.31) и результаты измерений занесите в табл.1. В этой же таблице запишите приборную ошибку измерения диаметра, т. е. Dd_пр .

2.Наденьте петлю, имеющуюся на нити с грузом, на штырь большего
шкива 5.

3. Предварительно (если потребуется) намотайте нить на шкив так, чтобы груз касался пола и нить была натянута. В этом положении начертите мелом на маховике 1 (рис.31) горизонтальную черту, что позволит отсчитывать число оборотов маховика.

4. Намотайте нить с грузом на шкив 5, одновременно отсчитывая по меловой черте число полных оборотов n₁ маховика. При этом груз поднимется на некоторую высоту h.

5. Измерьте высоту подъема груза длинной линейкой, поставленной строго вертикально.

При проведении последующих измерений следите, чтобы число полных оборотов n₁ сохранялось неизменным и высоты отличались друг от друга не больше, чем на 2 мм (Dh ≤ 2мм).

Значения величин h и n₁ занесите в табл.1.

6. Измерьте не менее 5 раз время падения груза с высоты h (включите секундомер в момент начала движения груза и выключите в момент касания грузом пола). Результаты измерения времени движения груза занесите в табл.2. Также необходимо записать приборную ошибку измерения времени (Dt_пр ) и субъективную ошибку (Dt_суб. ).

7. Подсчитайте по меловой черте число оборотов n₂ маховика от момента касания грузом пола до полной остановки маховика. Следите за тем, чтобы нить обязательно соскочила со шкива. Число оборотов n₂ , округлив до ¼ оборота, занесите в табл.2.

8. Рассчитайте абсолютные и относительные ошибки прямых измерений диаметра шкива, времени падения груза и числа полных оборотов маховика до остановки по соответствующим формулам:

, , %.

, , %.

, .

9.Повторите п.п. 1÷8 для меньшего шкива 6 (рис.31).

10.По средним значениям величин, входящих в расчетную формулу (18), рассчитайте среднее значение момента инерции маховика как при использовании большего шкива 5, так и меньшего шкива 6.

11.Рассчитайте относительную погрешность DI/I по формуле:

,

где m = 610 г — масса груза;

Dm = 0,5 г — абсолютная погрешность измерения массы груза.

В расчетной формуле относительной погрешности DI/I не учитывается относительная погрешность величины ускорения свободного падения (Dg/g). Попробуйте убедиться, что указанная погрешность пренебрежимо мала.

12.Рассчитайте абсолютную погрешность DI.

13.Запишите конечный результат в стандартном виде

1. Сформулируйте цель данной лабораторной работы.

2. Какое тело называется абсолютно твердым ?

3. Какое движение называется поступательным ?

4. Назовите меру инертности тела при поступательном движении.

5. Назовите меру инертности тела при его вращательном движении относительно неподвижной оси.

6. Напишите формулу момента инерции системы материальных точек
относительно оси.

7. По какой формуле удобно вычислять момент инерции однородного тела
(цилиндра, шара и т.д.) относительно оси симметрии этого тела ?

8. Оцените момент инерции относительно оси системы из трех тел, если по
отдельности моменты инерции тел относительно этой оси равны I₁ , I₂ , I₃ .

9. Укажите единицу измерения момента инерции в СИ.

10. Дайте определение момента силы относительно точки (центра).

11. Какую величину называют плечом силы ?

12. Дайте определение момента силы относительно оси.

13. Какую величину называют моментом импульса ?

14. Сформулируйте закон сохранения механической энергии.

15. Укажите различия между консервативными и диссипативными силами.

16. Назовите причину изменения полной механической энергии.

17. Выполняется ли закон сохранения механической энергии при движении
маховика ?

18. Напишите формулу изменения полной механической энергии для данной
экспериментальной установки.

19. Дайте определение работы постоянной силы.

20. В каком случае работа силы отрицательна ?

21. Как оценивается работа силы трения для данной экспериментальной
установки, если маховик совершит n оборотов ?

22. Напишите формулу кинетической энергии вращающегося тела.

23. В какие виды энергии переходит потенциальная энергия поднятого груза ?

24. Выведите расчетную формулу.

25. Перечислите величины, измеряемые в данной работе с помощью прямых
измерений.

26. Перечислите виды погрешностей измерений.

27. Назовите виды измерений физических величин.

28. Как вычисляются абсолютные и относительные ошибки при прямых
измерениях ?

29. Что такое доверительный интервал ?

30. Напишите формулу для вычисления относительной погрешности момента инерции маховика .

📽️ Видео

Урок 94. Вычисление моментов инерции телСкачать

Задача на маховик [Физзадачи #32]Скачать

Момент инерцииСкачать

Самораскручивание маховика с переменным моментом инерции после полной остановки.Скачать

Урок 93. Основное уравнение динамики вращательного движенияСкачать

Основное уравнение динамики вращательного движения. 10 класс.Скачать

Момент инерции абсолютно твердого тела. Практическая часть. 10 класс.Скачать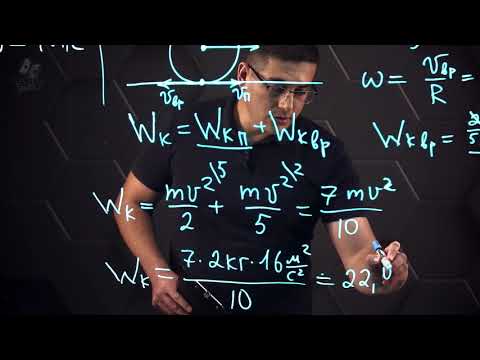

Маховик с переменным моментом инерции-движение жидкости.Скачать

Моменты силы, импульса, инерции. Динамика вращательного движенияСкачать

Момент инерции абсолютно твердого тела. 10 класс.Скачать

Маховик с переменным моментом инерции как БТГ.Скачать

Уравнение движенияСкачать

Вращательное движение. 10 класс.Скачать

Поступательное и вращательное движения.Скачать

Урок 98. Задачи на вычисление моментов инерции (ч.1)Скачать

ИнерцияСкачать

Урок 100. Задачи на вращение твердого тела (ч.1)Скачать