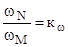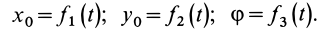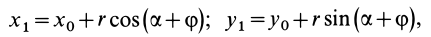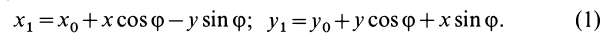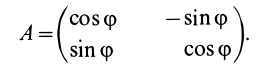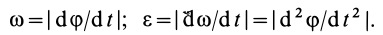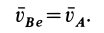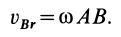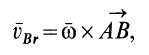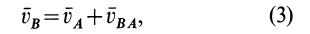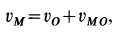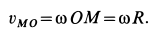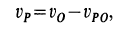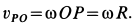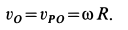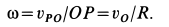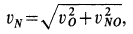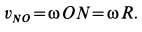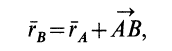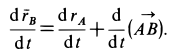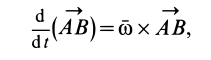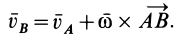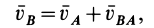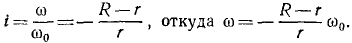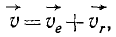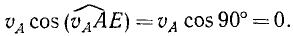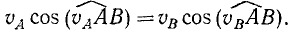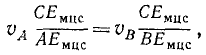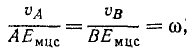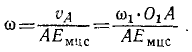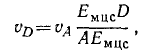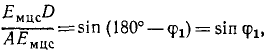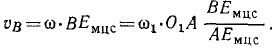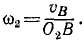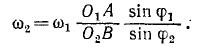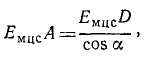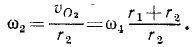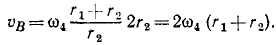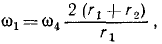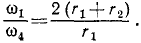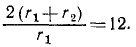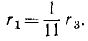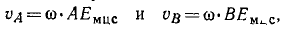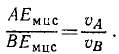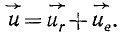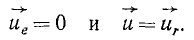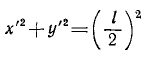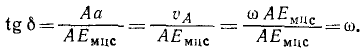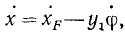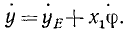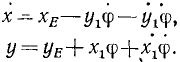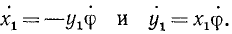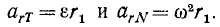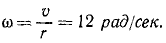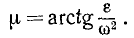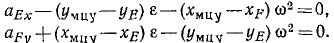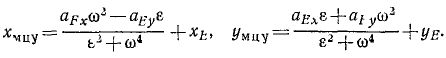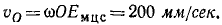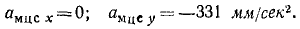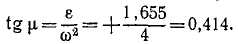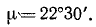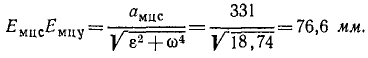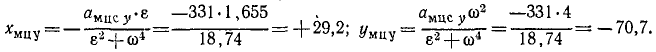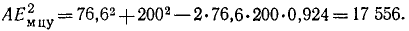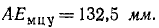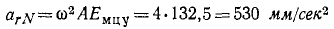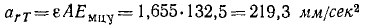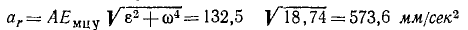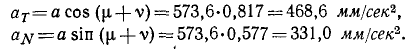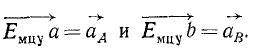В зависимости от приложенного к колесу момента различают: колесо ведомое (М=0), ведущее (М=Мк-крутящий момент) и тормозное (М=Мт- тормозной момент).
Рассмотрим уравнения мощностей и сил, приложенных к каждому из этих колес.
Ведомое колесо
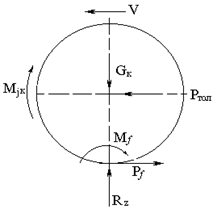
Если колесо будет двигаться с ускорением, тогда дополнительно возникнет инерционный момент
Мj к = 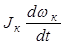
где Jк – момент инерции колеса относительно оси вращения;
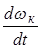
Рис 3.3 Ведомое колесо
Составим уравнения мощностей, считая, что подводимая к колесу мощность расходуется на преодоление сопротивления качению и разгон колеса. Тогда
где N тол – мощность, создаваемая толкающей силой Ртол , и равная
Njк – мощность, вызванная инерционным моментом
Njк = Мjк × wк = Jк 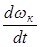
где wк – угловая скорость вращения колеса.
Подставив полученные выражения в уравнение (3.2), имеем
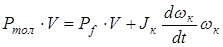
Если правую и левую стороны уравнения (3.3) разделить на V, учитывая, что V = wк×rк , тогда получим уравнение сил, действующих на ведомое колесо
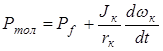
При равномерном движении колеса это уравнение запишется так
Ведущее колесо
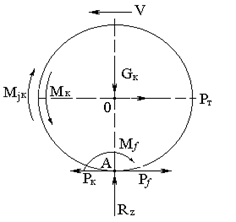
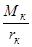
Рис.3.4 Ведущее колесо
Со стороны опорной поверхности действуют равнодействующая нормальных реакций Rz , сила сопротивления качению Рf и момент сопротивления качению Мf. При ускоренном движении возникает дополнительно инерционный момент Мj к.
Составим уравнение мощностей, учитывая, что подводимая к колесу через крутящий момент мощность расходуется на преодоление сопротивления качению колеса, создание тяговой силы и разгон колеса
Мощности Nf = Pf×V и Nj к= Jк 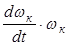
После подстановки этих значений в уравнение (3.4) и деления уравнения на скорость V, получим уравнение сил, действующих на ведущее колесо
Рк = Рf + Pт + 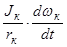
Если движение колеса равномерное, тогда 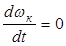
Из уравнения (3.6) имеем
Из анализа уравнения (3.7) следует, что тяговая сила зависит от свойств опорной поверхности и всегда меньше окружной силы, которая создается крутящим моментом двигателя.
Из анализа рис.3.4 видно, что окружная сила Рк и сила сопротивления качению Рf имеют противоположные направления. Их результирующая в точке А контакта колеса с дорогой Рк – Рf будет ограничена силой сцепления колеса с дорогой, равной j ×Rz ( j — коэффициент сцепления шины с опорной поверхностью). Следовательно, максимальное значение тяговой силы ограничено сцепными возможностями колеса с опорной поверхностью и определяется по формуле PT max = j ×Rz..
Тогда максимальная окружная сила, создаваемая крутящим моментом двигателя, которая ограничена сцепными возможностями шины, запишется
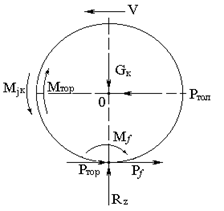
Расчетная схема сил, действующих на тормозное колесо, приведена на рис.3.5. На тормозное колесо действует тормозной момент Мтор, который вызывает тангенциальные реакции опорной поверхности. Равнодействующую этих реакций принято называть тормозной силой, равной 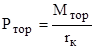

Рис. 3.5 Тормозное колесо
Инерционный момент Мjк в этом случае будет действовать по ходу движения колеса вперед, а толкающая сила Ртол со стороны автомобиля будет направлена по вектору скорости.
С учетом направления сил уравнение мощностей, действующих на тормозное колесо, запишется Nтор + Nf = Nтол + Njк, (3.8)
где Nтор – мощность, создаваемая тормозным моментом, которая определяется по формуле Nтор= Мтор×wк = 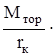
Nтол – мощность, создаваемая толкающей силой, приложенной к центру колеса
Njк – мощность, создаваемая инерционным моментом колеса
Nj к = 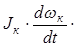
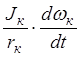
1.Гришкевия А.И. Автомобили: Теория.-Минск: Вышэйш. Шк., 1986.-240с., с.-10…26.
2. Литвинов А.С., Фаробин Я.Е. Автомобиль: Теория эксплуатационных свойств.-М.: Машиностроение, 1984.-272 с., с.-21-38.
4. Характеристика источника энергии
Источником энергии на автомобиле является двигатель внутреннего сгорания (ДВС): карбюраторный, инжекторный или дизельный. Принципиальное различие в работе этих двигателей заключается в том, что в карбюраторном и инжекторном двигателях воспламенение горючей смеси происходит от энергии электрической искры, а в дизеле – от температуры сжатого воздуха.
В общем случае ДВС характеризуются энергоемкостью, динамичностью и экономичностью. Энергоемкость определяется зависимостью мощности двигателя Ne от угловой скорости вращения коленчатого вала wе. Динамичность описывается зависимостью крутящего момента двигателя Ме, от угловой скорости коленчатого вала wе. Экономичность определяется зависимостью удельного расхода топлива qе от угловой скорости коленчатого вала двигателя wе.
Основной характеристикой двигателя является его внешняя скоростная характеристика – графики зависимости мощности Ne, крутящего момента Ме, удельного расхода топлива qе от угловой скорости коленчатого вала wе при максимальной подаче топлива. Эта характеристика двигателя и описывает его энергоемкость, динамичность и топливную экономичность.
Внешняя скоростная характеристика вновь созданного двигателя определяется экспериментально на заводах по производству двигателей. Эту характеристику двигателей постоянно контролируют в процессе прозводства, определяя ее экспериментально на стендах выборочно из партии произведенных двигателей.
Внешняя скоростная характеристика двигателя представлена на рис.4.1
Выделим следующие характерные точки на этой характеристике:
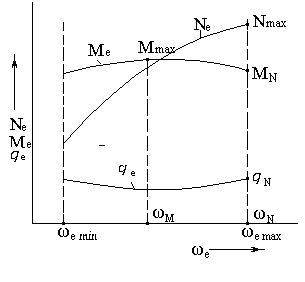
wN – угловая скорость в рад/с, соответствующая максимальной мощности двигателя ( рад./с);
Мmax – максимальный крутящий момент двигателя (Нм);
wМ – угловая скорость, соответствующая максимальному крутящему моменту (рад./с);
МN – момент, соответствующий
максимальной мощности двигателя (Нм);
qN – удельный расход топлива в г/кВт×ч, соответствующий максимальной мощности.
Рис. 4.1 Внешняя скоростная характеристика двигателя
Введем два экспериментальных коэффициента, которые определяются из внешней скоростной характеристики двигателя,
кМ = 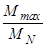
кw = 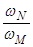
Для двигателей, применяемых на автомобилях, значения этих коэффициентов находятся в пределах км= 1,05…1,5 и кw = 1,5…2,5.
Для практических расчетов зависимости Ne= f (we) и Mе= f (we) математически описываются параболами третьего и второго порядков
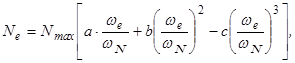
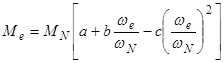
Неизвестными величинами в формулах (4.1) и (4.2) являются коэффициенты а, b, c.
Определим эти коэффициенты, рассмотрев режимы работы двигателя при wе=wN ,we=wM, а также исследовав функцию Ме= f (we) на экстремум.
Если зададим угловую скорость двигателя we=wN, тогда мощность, развиваемая двигателем, достигает максимального значения Ne=Nmax .
После подстановки этих условий в уравнение (4.1), имеем
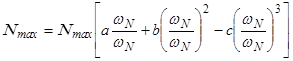
После сокращений получим 1 = а + b – c.
Если зададим угловую скорость двигателя we=wM, тогда крутящий момент двигателя достигнет максимального значения Ме = Мmax.
После подстановки этих условий в уравнение (4.2) имеем
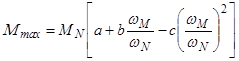
или 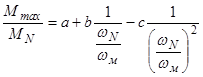
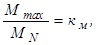
имеем 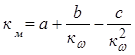
Для получения третьего уравнения, необходимого для определения коэффициентов а, b, c, исследуем уравнение (4.2) на экстремум.
Для чего приравняем 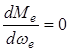
Взяв производную с уравнения (4.2), получим
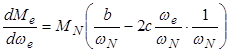
Если 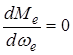
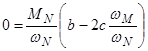
Условие выше приведенной зависимости будет выполняться, если 
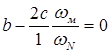
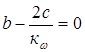
В результате приведенных исследований получена система из трех уравнений с тремя неизвестными а,b,c.
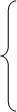
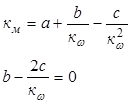
Решая эту систему, получим
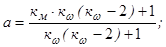
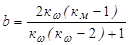
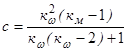
Поскольку входящие в уравнения (4.7) коэффициенты кw и км являются экспериментальными, поэтому и коэффициенты а,b,c также являются экспериментальными. На заводах по производству двигателей экспериментально определяется внешняя скоростная характеристика, а затем по этой характеристике с учетом зависимостей (4.7) рассчитываются коэффициенты а,b,c. Каждый тип двигателей имеет характерные только для него значения коэффициентов а,b,c. Эти коэффициенты представлены в справочной литературе.
Для определения удельного расхода топлива в зависимости от угловой скорости коленчатого вала wе рекомендуется воспользоваться эмпирической зависимостью
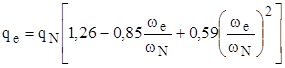
где qN – удельный расход топлива при максимальной мощности в г/кВт×ч, который для дизельных двигателей принимается 210¸240 г/кВт×ч, а для карбюраторных двигателей — 310¸340 г/кВт×ч.
В табл. 4.1 приведены значения параметров двигателей.
Таблица 4.1 Параметры карбюраторных и дизельных двигателей
| Марка | Vл ,л | Тип | Nemax, кВт | 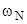 , рад/с , рад/с | Меmax, Н.м | Км | 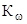 | Коэффициенты | ||
| а | b | с | ||||||||
| ВАЗ-2103 ВАЗ-2106 ВАЗ-2108 М-412 ЗМЗ-24Д ЗМЗ-66 ЗИЛ-130 ЗИЛ-375 КамАЗ-740 ЯМЗ-236 ЯМЗ-238 ЯМЗ-238Н ЯМЗ-240 | 1,45 1,57 1,3 1,48 2,445 4,25 6,00 7,00 10,85 11,15 14,86 14,86 22,30 | К4Р К4Р К4Р К4Р К4Р К8V К8V K8V Д8V Д6V Д8V Д8V Д12V | 56,6 58,8 48,8 55,2 69,9 84,6 110,3 132,4 154,6 132,4 176,5 220,6 264,8 | 586,4 565,5 586 607,4 471,2 345,4 335,1 335,1 272,2 219,9 219,9 219,9 219,9 | 105,1 121,6 95,2 111,2 186,3 284,4 402,0 465,0 637,6 666,7 882,6 1078,7 1274,8 | 1,088 1,16 1,19 1,22 1,26 1,16 1,22 1,18 1,12 1,107 1,099 1,075 1,061 | 1,6 1,8 1,19 1,8 1,87 1,47 1,68 1,68 1,6 1,4 1,4 1,4 1,4 | 0,84 0,91 0,64 0,97 0,85 0,44 0,75 0,80 0,68 0,44 0,48 0,61 0,68 | 0,78 0,9 1,75 0,98 1,46 2,12 1,59 1,3 1,38 1,87 1,73 1,31 1,07 | 0,62 0,81 1,39 0,95 1,31 1,56 1,34 1,10 1,06 1,31 1,21 0,92 0,75 |
Заметим, что приведенные выше параметры двигателей определялись на стендовом оборудовании. В реальных условиях эксплуатации на автомобиле двигатель работает с другими впускной и выпускной системами, на нем установлено дополнительное оборудование, для привода которого затрачивается дополнительная мощность. Поэтому эффективная мощность, развиваемая двигателем на автомобиле, несколько меньшая. Однако, как показал анализ литературных источников, это уменьшение не превышает 15%.
1. Гришкевич А.И. Автомобили: Теория.- Минск: Вышэйш шк.,1986.-240 с., с.-28…30.
2. Кошарний М.Ф. Основи механіки та енергетики автомобіля. -К.: Вища шк., 1992.-200 с., с. –22-30.
3. Литвинов А.С., Фаробин Я.Е. Автомобиль: Теория эксплуатационных свойств.-М.: Машиностроение, 1984.-272 с., с.-28-31.
1.Какие типы двигателей применяются на автомобилях?
2. В чем принципиальное отличие карбюраторного и инжекторного двигателей от дизельного?
3. Что такое внешняя скоростная характеристика двигателя?
4.Каким образом определяются коэффициенты приспосабливаемости двигателей по частоте и крутящему моменту?
5.Каким образом рассчитываются коэффициенты а,в,с ?
- Решение задач на движение тел по наклонной плоскости
- Плоское движение твердого тела в теоретической механике
- Уравнения плоского движения твердого тела
- Разложение плоского движения твердого тела на поступательное и вращательное
- Угловая скорость и угловое ускорение тела при плоском движении
- Скорости точек тела при плоском движении
- Пример 1.
- Разложение плоского движения на поступательное и вращательное
- Плоское движение и его уравнение
- Задача №1
- Скорости и ускорения точек плоской фигуры
- Скорость точки фигуры в плоском составном движении
- Задача №2
- Задача №3
- Задача №4
- Задача №5
- Задача №6
- Задача №7
- Задача №8
- Задача №9
- Задача №10
- Скорости точек плоской фигуры можно определить графически планом скоростей
- Задача №11
- Задача №12
- Задача №13
- Мгновенный центр ускорений при плоском движении
- Задача №14
- Задача №15
- План ускорений
- Задача №16
- Задача №17
- Понятие об общем случае движения твердого тела
- Уравнение движения свободного тела
- 📽️ Видео
Видео:Уравнение движенияСкачать

Решение задач на движение тел по наклонной плоскости
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
Мы ежедневно сталкиваемся с движением по наклонной плоскости, когда транспорт едет с горы или в гору, при проведении лабораторных работ, и сегодня мы рассмотрим, как решаются задачи на движение тел по наклонной плоскости.
Видео:Основное уравнение динамики вращательного движения. 10 класс.Скачать

Плоское движение твердого тела в теоретической механике
Содержание:
Плоское движение твердого тела:
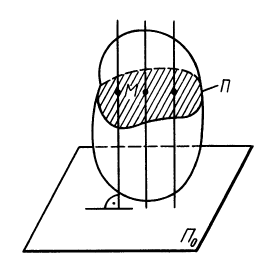
Плоским движением твердого тела называют такое его движение, при котором каждая его точка все время движется в одной и той же плоскости. Плоскости, в которых движутся отдельные точки, параллельны между собой и параллельны одной и той же неподвижной плоскости. Поэтому плоское движение твердого тела часто называют плоскопараллельным движением. Траектории точек тела при плоском движении являются плоскими кривыми.
Плоское движение твердого тела имеет большое значение в технике, так как звенья большинства механизмов и машин, применяемых в технике, совершают плоское движение. Вращательное движение твердого тела вокруг неподвижной оси можно считать частным случаем плоского движения.
При изучении плоского движения, как и любого другого, необходимо рассмотреть способы задания этого движения, а также приемы вычисления скоростей и ускорений точек тела.
Рис. 41
Пусть твердое тело совершает плоское движение, параллельное неподвижной плоскости
Следовательно, для изучения движения точек, лежащих на рассматриваемой прямой, достаточно изучить движение одной точки этой прямой, например точки 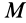
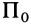
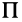
Таким образом, для изучения плоского движения твердого тела достаточно изучить движение плоской фигуры в ее плоскости, параллельной неподвижной плоскости 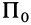
Видео:Скатывание тела (колеса, цилиндра) по наклонной плоскостиСкачать

Уравнения плоского движения твердого тела
Для задания положения плоской фигуры на плоскости относительно системы координат 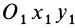
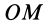
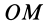
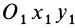
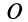
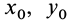
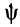
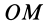
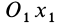
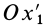
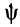
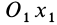
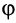
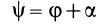
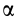
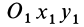
Рис. 42
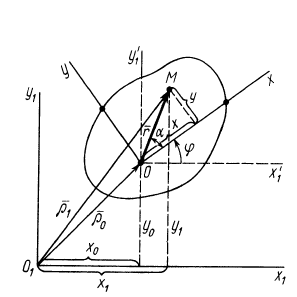
Положение любой точки 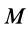
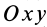
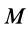
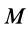
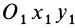
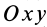
где 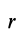
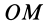
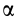
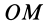
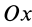
Раскрывая косинус и синус суммы двух углов и учитывая, что 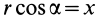
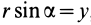
Формулы (1) являются уравнениями движения точки плоской фигуры относительно системы координат 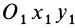
Эти формулы позволяют определить координаты любой точки плоской фигуры по заданным уравнениям движения этой фигуры и координатам ее точки относительно подвижной системы координат, скрепленной с движущейся фигурой.
Используя векторно-матричную символику, (1) можно выразить в форме
где 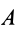
Разложение плоского движения твердого тела на поступательное и вращательное
Любое движение твердого тела, в том числе и движение плоской фигуры в ее плоскости, бесчисленным множеством способов можно разложить на два движения, одно из которых переносное, а другое — относительное. В частности, движение плоской фигуры в ее плоскости относительно системы координат 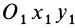
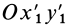
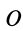
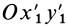
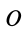
Для доказательства этого достаточно показать, что плоскую фигуру в ее плоскости из одного положения в любое другое, в том числе и бесконечно близкое первому, можно перевести двумя перемещениями — поступательным перемещением в плоскости фигуры вместе с каким-либо полюсом и поворотом в той же плоскости вокруг этого полюса. Рассмотрим два любых положения плоской фигуры I и II в ее плоскости, определяемые двумя положениями отрезка 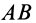
В общем случае, когда отрезок 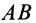
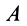
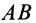
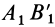
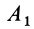
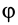
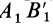
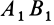
В частном случае, когда отрезок 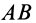
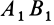
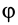
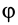
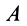
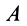
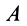
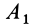
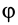
Действительное плоское перемещение фигуры из положения I в положение II может быть любым, но его всегда можно заменить двумя простыми плоскими перемещениями — поступательным и вращательным — так, чтобы конечное положение плоской фигуры в обоих случаях было одним и тем же.
Действительное перемещение фигуры в ее плоскости из одного положения в другое, бесконечно близкое к первому, в пределе можно точно заменить двумя элементарными простыми плоскими перемещениями — поступательным и вращательным. При этом поступательное перемещение фигуры вместе с какой-либо ее точкой является переносным движением плоской фигуры, а вращение фигуры вокруг подвижной оси, перпендикулярной плоскости фигуры и проходящей через выбранную точку, относительным движением.
Поступательное перемещение зависит от выбора точки фигуры, вместе с которой совершается это поступательное перемещение, в то время как угол поворота вокруг полюса не зависит от выбора полюса.
На рис. 43 показаны случаи, когда за полюсы выбираются сначала точка 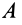
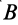
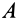
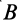
Угловая скорость и угловое ускорение тела при плоском движении
Для характеристики вращательной части плоского движения твердого тела вокруг подвижной оси, проходящей через выбранный полюс, аналогично случаю вращения твердого тела вокруг неподвижной оси можно ввести понятия угловой скорости 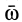
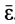
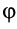
Так как вращательная часть движения не зависит от выбора полюса, то и характеристики этой части движения — угловая скорость и угловое ускорение — также не зависят от выбора полюса. Следовательно, для заданного плоского движения фигуры в данный момент они одинаковы относительно подвижной оси, проходящей через любую точку фигуры.
При плоском движении тела угловую скорость и угловое ускорение можно считать векторами, направленными по подвижной оси, перпендикулярной плоскости фигуры и проходящей через выбранный полюс. Вектор угловой скорости 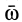
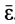
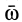
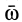
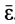
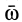
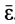
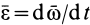
Скорости точек тела при плоском движении
Применяя к плоскому движению теорему о сложении скоростей для какой-либо точки 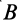
где 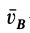
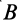
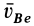
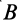
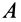
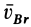
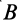
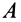
Так как за переносное движение выбрано поступательное движение вместе с точкой 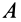
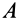
Скорость относительного движения, в случае когда оно является вращательным движением, равна
Скорость 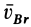
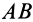
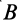
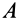
где угловая скорость 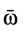
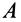
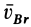
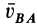
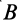
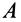
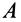
а вектор 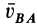
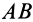
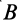
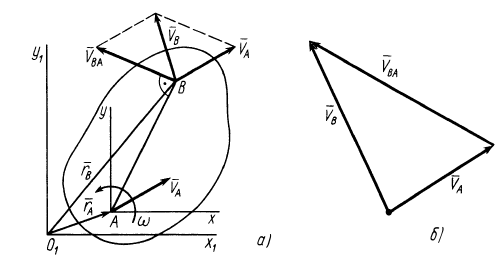
Таким образом, скорость какой-либо точки фигуры при ее плоском движении равна векторной сумме скорости полюса и относительной скорости этой точки от вращения фигуры вокруг полюса. Формула (3) выражает зависимость между скоростями двух любых точек тела при плоском движении в любой момент времени.
Рис. 44
Рис. 45
Пример 1.
Колесо радиусом 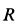
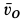
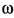
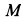
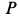
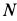
Решение. Для точки 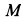
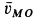
Для точки 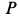
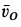
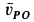
При качении колеса по прямой линии без скольжения скорость точки 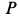
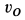
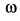
Отсюда угловую скорость можно выразить через скорость центра колеса 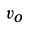
В точке 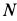
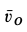
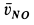
Отметим, что при качении колеса по прямой без скольжения скорости точек обода колеса не направлены по касательной к ободу, за исключением самой верхней его точки 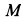
Формулу (3), устанавливающую зависимость скоростей двух точек плоской фигуры, можно получить непосредственным дифференцированием по времени векторного равенства
справедливого для любого момента времени (см. рис. 44, а).
При дифференцировании векторов учитываем их изменения относительно основной, неподвижной, системы координат 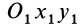
Очевидно, 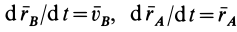
Вектор 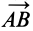
где 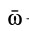
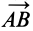
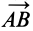
Если ввести обозначение 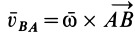
т. е. получаем формулу (3).
Разложение плоского движения на поступательное и вращательное
Плоским движением называют движение твердого тела, при котором все точки тела движутся только в плоскостях, параллельных данной неподвижной плоскости
Плоское движение и его уравнение
Ознакомление с плоским движением твердого тела начнем с частного примера. Представим себе, что закрытая книга лежит на столе. Не раскрывая книги, будем перемещать ее по поверхности стола, но так, чтобы контакт книги со столом ни в одной точке не нарушился; в остальном движение книги произвольно. При этом условии частицы книги опишут траектории, лежащие в плоскостях, параллельных плоскости стола, и каждая страница будет двигаться в той плоскости, в которой она находилась до начала движения. Такое движение книги назовем плоским.
Вообще плоским движением называют такое движение твердого тела, при котором все точки тела движутся в плоскостях, параллельных некоторой неподвижной плоскости. Каждую из этих плоскостей можно назвать плоскостью движения тела. Вращение является одним из частных случаев плоского движения тела.
Плоское движение часто встречается в технике. Большинство современных механизмов имеет звенья, совершающие только плоские движения. Такие механизмы называют плоскими.
Плоское движение твердого тела иногда называют плоскопараллельным движением, или движением параллельно неподвижной плоскости. Все эти термины идентичны.
Плоское движение тела характеризуется движением фигуры, полученной от пересечения тела плоскостью, в которой лежит траектория какой-либо из точек тела
Если тело, находящееся в состоянии плоского движения, пересечь плоскостью, в которой лежит траектория какой-нибудь из его точек, то плоская фигура, получившаяся от пересечения тела, будет передвигаться только в этой плоскости. Движения точек тела, лежащих на перпендикуляре, восставленном к плоскости фигуры, совершенно одинаковы, а потому движение тела может быть охарактеризовано движением фигуры в ее плоскости, и для исследования плоского движения тела достаточно исследовать движение плоской фигуры, полученной при пересечении тела одной из этих плоскостей. Так, в приведенном примере движение книги вполне определяется движением какой-либо из ее страниц в плоскости, параллельной плоскости стола.
Это обстоятельство позволяет заменить изучение плоского движения тела изучением движения плоской фигуры в ее плоскости.
Движение плоской фигуры можно рассматривать как составное, состоящее из переносного поступательного н относительного вращательного
Пусть плоская фигура (рис. 136) движется в плоскости хОу относительно основной системы координат. Примем какую-либо точку E этой фигуры за начало подвижной системы отсчета и назовем эту точку полюсом. Построим в точке E систему декартовых координат х’Еу’, неизменно связанную с фигурой.
Для определения положения фигуры на плоскости хОу достаточно знать положение системы отсчета х’Еу’, т. е. координаты (хЕ и уЕ) точки Е, и угол, на который повернута фигура, например угол φ между положительными направлениями осей Ox и Ex’. По мере движения фигуры положение подвижной системы координат х’Еу’ относительно неподвижной системы хОу изменяется и, чтобы определить движение фигуры, нужно знать эти величины как некоторые не прерывные однозначные функции времени:
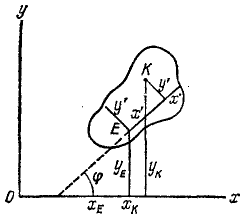
Рис. 136
Эти уравнения являются уравнениями движения плоской фигуры в ее плоскости, следовательно, они определяют плоское движение твердого тела.
Обратим внимание на то, что уравнения (112′) и (112″) тождественны с уравнениями (58′) и (58″) движения точки по плоскости или с уравнениями (77) плоского поступательного движения; уравнение же (112″‘) тождественно с уравнением (81) вращения вокруг неподвижной оси. Это наводит на мысль рассматривать движение плоской фигуры как составное движение, состоящее из переносного поступательного движения, определяемого движением полюса Е, и относительного вращательного движения вокруг полюса, точнее, вокруг оси, проходящей через полюс перпендикулярно к плоскости фигуры. Поэтому движение плоской фигуры в ее плоскости часто рассматривают как составное и искусственно раскладывают его на два движения, причем переносное обычно выбирают поступательным, а относительное— вращательным.
Такое разложение плоского движения очень удобно и, несмотря на то что оно является чисто искусственным, его широко применяют при решении различных конкретных задач. В частности, преимущества разложения плоского движения на переносное поступательное и относительное вращательное заключаются в том, что при таком разложении кориолисово ускорение всякой точки фигуры равно нулю, а также равны нулю переносные угловая скорость и угловое ускорение фигуры, а потому угловая скорость и угловое ускорение фигуры в ее относительном вращательном движении вокруг полюса оказываются равными соответственно абсолютным угловой скорости п угловому ускорению фигуры.
Задача №1
Шестеренка радиуса r, катящаяся внутри неподвижной шестеренки радиуса R, приводится в движение кривошипом OA, вращающимся равномерно вокруг оси О неподвижной шестеренки с угловой скоростью ω0. При t=0 кривошип расположен вдоль оси Ox (рис. 137). Составить уравнение движения подвижной шестеренки, принимая ее центр за полюс.
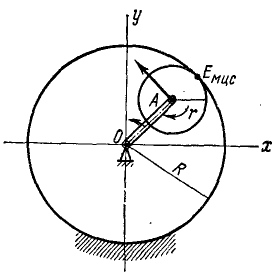
Рис. 137
Решение. Шестеренка совершает плоское движение, которое будем рассматривать как составное, состоящее из переносного кругового поступательного движения, определяемого движением точки А, и относительного вращательного движения вокруг точки А. Принятая нами за полюс точка А принадлежит одновременно и шестеренке радиуса r и кривошипу OA. Вращаясь с постоянной угловой скоростью ω0, кривошип OA за время t повернется от начального горизонтального положения на угол ωot и координаты полюса в мгновение t будут:
x = OA cos ωot = (R- r) cos ωot,
Эти координаты — функции времени, следовательно, написанные равенства представляют уравнения движения полюса А, или, что то же, уравнения переносного поступательного движения шестеренки.
Вращение шестеренки вокруг полюса происходит с иной угловой скоростью ω, чем вращение кривошипа, и, поскольку зацепление внутреннее, — в противоположную сторону. В данном случае кривошип вращается в положительном направлении, а шестеренка—в отрицательном. Предполагается, что шестеренка катится без скольжения, а потому, согласно известной из элементарной физики формуле, передаточное отношение
Заменяя 2 r точек фигуры при ее вращении относительно полюса зависят не только от угла поворота φ фигуры и его производных ω и ε, но также и от расстояния r точек от полюса, а следовательно, и от выбора полюса. Таким образом, хотя угол поворота фигуры, угловая скорость и угловое ускорение фигуры не зависят от выбора полюса, относительные движения, скорости и ускорения точек фигуры зависят от этого выбора.
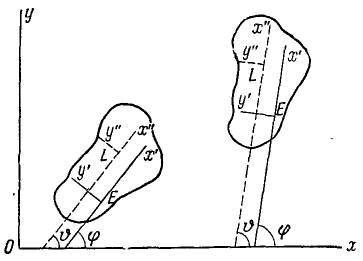
Рис. 139
Скорости и ускорения точек плоской фигуры
Скорость любой точки фигуры, находящейся в плоском движении, равна геометрической сумме скорости этой точки относительно полюса и скорости полюса
Скорость точки фигуры в плоском составном движении
Пусть плоская фигура вместе с нанесенными на ней координатными осями х’Еу’ движется в плоскости основной системы координат (см. рис. 136). Пусть К—какая-либо точка плоской фигуры. Ее координаты х’ и y’ не изменяются, потому, что точка К и подвижная система х’Еу’ неизменно связаны с фигурой. Как известно из аналитической геометрии и как видно из рисунка, координаты точки К (х, у) связаны с координатами (x’, у’) той же точки соотношениями
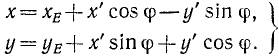
Для получения проекций скорости на неподвижные оси координат продифференцируем по времени равенства (113), рассматривая φ как функцию времени:
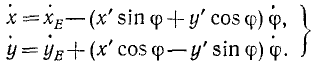
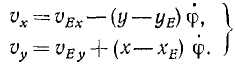
Последние члены правых частей выражают согласно формулам Эйлера (79) проекции вращательной скорости точки К при вращении фигуры вокруг полюса.
Следовательно, вектор абсолютной скорости любой точки K плоской фигуры равен геометрической сумме двух векторов: 1) переносной скорости в поступательном движении, равной скорости какой-либо точки Е, неизменно связанной с фигурой и принятой за полюс, н 2) относительной скорости во вращательном движении фигуры вокруг полюса Е. Теорему параллелограмма скоростей для любой точки К плоской фигуры запишем так:
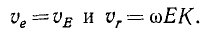
Относительная скорость vr точки К относительно точки Е, как всякая вращательная скорость, направлена перпендикулярно к EK в сторону вращения фигуры.
Выясним, как зависят скорости точек плоской фигуры от выбора полюса. Абсолютные скорости точек, очевидно, не могут зависеть от выбора полюса: они существуют объективно и обусловлены только физическими причинами. Переносные скорости всех точек равны скорости полюса, а следовательно, зависят от полюса. Относительные скорости точек фигуры равны произведению угловой скорости (не зависящей от полюса) фигуры на их расстояния от полюса.
Так, например, на рис. 140, а изображены абсолютные скорости точек А, В, С, D, F некоторой плоской фигуры, движущейся в своей плоскости. Эти скорости зависят только от движения фигуры и, конечно, не могут зависеть от метода их определения. Рассмотрим эти скорости как составные. Если мы примем за полюс точку F, то получим параллелограммы скоростей, представленные на рис. 140, б. Если же примем за полюс точку А, то получим параллелограммы скоростей, изображенные на рис. 140, в. Диагонали параллелограммов (абсолютные скорости) не зависят от тех составляющих скоростей, на которые мы их разлагаем. На каждом из рисунков переносные скорости точек плоской фигуры одинаковы и равны скорости полюса. Относительные скорости точек фигуры различны. Они равны произведению угловой скорости ω на расстояние точки от полюса и направлены перпендикулярно к отрезку прямой, соединяющему точку с полюсом. 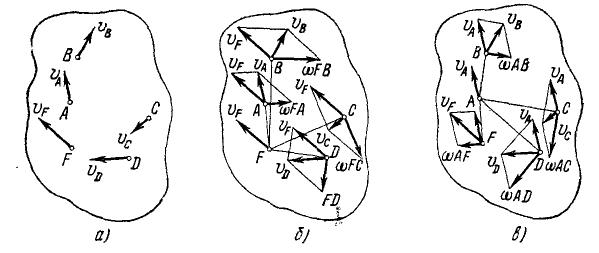
Рис. 140
Так, например, на рис. 140, а изображены абсолютные скорости точек А, В, С, D, F некоторой плоской фигуры, движущейся в своей плоскости. Эти скорости зависят только от движения фигуры и, конечно, не могут зависеть от метода их определения. Рассмотрим эти скорости как составные. Если мы примем за полюс точку F, то получим параллелограммы скоростей, представленные на рис. 140, б. Если же примем за полюс точку А, то получим параллелограммы скоростей, изображенные на рис. 140, в. Диагонали параллелограммов (абсолютные скорости) не зависят от тех составляющих скоростей, на которые мы их разлагаем. На каждом из рисунков переносные скорости точек плоской фигуры одинаковы и равны скорости полюса. Относительные скорости точек фигуры различны. Они равны произведению угловой скорости ω на расстояние точки от полюса и направлены перпендикулярно к отрезку прямой, соединяющему точку с полюсом.
Мгновенный центр скоростей. Пусть какая-либо плоская фигура движется относительно своей плоскости, принятой нами за неподвижную. Будем считать, что эта фигура имеет неограниченные размеры, или, что то же, соединим фигуру неизменно с подвижной плоскостью, которая движется вместе с этой фигурой в той же неподвижной плоскости. Возьмем на фигуре две произвольные точки А и В и к их скоростям υА и υВ (рис. 141, а) восставим перпендикуляры до пересечения в какой-то точке Е. Перпендикуляры к скоростям надо восставлять, разумеется, в точках их приложения, потому что скорость есть вектор прикрепленный.
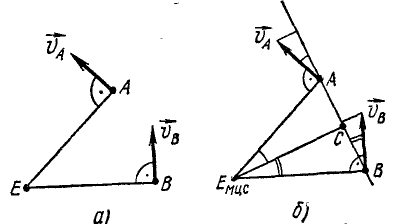
Рис. 141
Согласно основной теореме (77) кинематики твердого тела проекции скоростей всех точек прямой AE на эту прямую AE равны проекции 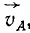
Аналогично равны нулю проекции на BE скоростей всех точек, составляющих прямую BE. Следовательно, скорости точек, составляющих прямые AE и BE, перпендикулярны этим прямым.
Скорость точки E равна нулю, потому что равны нулю ее проекции на две пересекающиеся прямые AE и BE. Назовем эту точку мгновенным центром скоростей и припишем ей индекс мцс:
υмцп = 0
В каждое мгновение на подвижной плоскости фигуры может быть только одна точка со скоростью, равной нулю, т. е. только один мгновенный центр скоростей.
Во всякое данное мгновение скорости точек фигуры, совершающей плоское движение, являются вращательными вокруг мцс
Соединим точки A и В прямой (рис. 141, б) и спроецируем на нее скорости точек Aи В:
Опустим перпендикуляр из Emuc на АВ. Тогда, выражая косинусы отношением сторон, получим
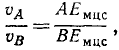
т. е. величины скоростей точек фигуры пропорциональны расстояниям этих точек от мгновенного центра скоростей. Этот вывод можно сделать и из условий неизменяемости фигуры. В самом деле, если фигура движется в своей плоскости, а скорость одной из точек фигуры равна нулю (υмцп = 0), то скорости всех прочих точек должны быть пропорциональны расстоянию от мцс.
Таким образом, скорости точек плоской фигуры удовлетворяют сбоим признакам вращательных скоростей: они перпендикулярны и пропорциональны отрезкам, соединяющим эти точки с мгновенным центром скоростей.
Предыдущую пропорцию мы можем переписать так:
где ω —угловая скорость фигуры. Точки А и В взяты произвольно, поэтому полученный результат относится ко всем точкам фигуры.
Если сделанные нами построения не умещаются на площади движущейся фигуры, то это не ограничивает общности доказательств, так как эти построения могут быть сделаны не на фигуре, а на неизменно связанной с фигурой воображаемой подвижной плоскости.
Мгновенный центр скоростей играет важную роль в теории плоского движения. Ознакомимся с некоторыми методами, позволяющими найти эту точку на плоскости.
I. Положение мгновенного центра можно определить аналитически.
Задача №2
Определить координаты мгновенного центра скоростей, если известны уравнения (112) движения плоской фигуры.
Решение. Уравнения (114) выражают проекции скорости любой точки, координаты которой х и у. Скорость мгновенного центра скоростей равна нулю, обозначив его координаты через xмцп и yмцп, подставим в уравнения (114) вместо скорости точки нуль, а вместо координат точки —координаты мгновенного центра скоростей:
откуда непосредственно получим координаты мгновенного центра скоростей.
Ответ. 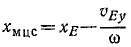
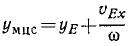
В этих равенствах хЕ и уЕ—координаты любой точки фигуры, a υFx и υEy — проекции абсолютной скорости той же точки.
II. Если известны угловая скорость ω фигуры и линейная скорость υk какой-либо одной точки К фигуры, то положение мгновенного центра скоростей можно определить, рассматривая скорость vκ как вращательную скорость вокруг мгновенного центра скоростей Eмцс. Мы найдем эту точку Eмцс, отложив от точки К перпендикулярно к скорости υk отрезок 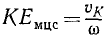
В самом деле, вращательная скорость точки перпендикулярна к отрезку прямой, соединяющей эту точку с центром, а длина этого отрезка равна отношению вращательной скорости точки к угловой скорости. Прямой угол между направлением скорости 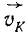
Задача №3
Диск радиуса r = 20 см (см. рис. 137, стр. 217), катящийся с угловой скорость ω=—50 ceκ -l внутри неподвижного обода радиуса R = 60 см, приводится в движение кривошипом OA, вращающимся равномерно вокруг центра О неподвижного обода с угловой скоростью ω0 = 25 ceκ -l . Найти мгновенный центр скоростей диска.
Решение. Известна угловая скорость диска и может быть определена скорость хотя бы одной из его точек. Такой точкой является палец А кривошипа OA. Точка А принадлежит не только диску, но и кривошипу, а потому ее скорость перпендикулярна к кривошипу и по модулю равна
Рассматривая скорость точки А как вращательную скорость точки диска вокруг его мгновенного центра скоростей, отложим перпендикулярно к ее скорости отрезок 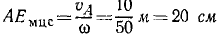
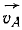
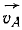
Ответ. Мгновенный центр находится в точке касания диска и неподвижного обода.
Мгновенный центр скоростей находится в точке пересечения перпендикуляров к скоростям точек фигуры
III. Распределение скоростей точек фигуры таково, как будто фигура вращается в данное мгновение вокруг мгновенного центра скоростей. Вращательные скорости точек перпендикуляр ны к радиусам траекторий этих точек, а все радиусы пересекаются в центре. Поэтому, чтобы найти мгновенный центр скоростей, достаточно восставить перпендикуляры к направлениям скоростей каких-либо точек фигуры. Точка их пересечения является мгновенным центром скоростей. Перпендикуляры к направлениям скоростей точек
надо восставлять, разумеется, в этих точках, так как скорость есть вектор закрепленный.
Задача №4
Стержни (рис. 142, a) O1A и O2B, соединенные со стержнем AB посредством шарниров А и В, могут вращаться вокруг неподвижных точек O1 и O2, оставаясь в одной плоскости (шарнирный четырехзвенник). Даны: длина кривошипа O1A и его угловая скорость ω1; длина коромысла O2B и углы φ1 и φ2, которые шатун AB образует с кривошипом и с коромыслом при данном положении механизма.
Найти построением ту точку D шатуна, скорость которой в данное мгновение направлена вдоль шатуна, определить величину этой скорости и угловую скорость ω2 коромысла O2B как функции углов φ1 и φ2.
Решение. Механизм состоит из четырех твердых звеньев (включая и станину O1O2); естественно, что угловые скорости различных звеньев могут быть различны.
Шарнир А принадлежит кривошипу O1A (рис. 142, б), его скорость перпендикулярна к O1A и по модулю равна υА = ω1O1A. Шарнир В принадлежит коромыслу O2B, и потому его скорость υB (неизвестная по величине) направлена перпендикулярно к O2B.
Но те же точки А и В принадлежат шатуну АВ, а следовательно, их скорости υА и и υB можно рассматривать как вращательные скорости вокруг мгновенного центра скоростей шатуна АВ. Перпендикуляры, восставленные в точках А и В к направлениям их скоростей, пересекаются в точке Eмцс (рис. 142, в), где, следовательно, и находится мгновенный центр скоростей. Скорость каждой точки шатуна перпендикулярна к отрезку прямой, соединяющему эту точку с мгновенным центром скоростей, и пропорциональна длине этого отрезка. Чтобы 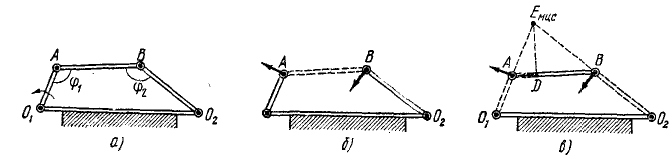
Рис. 142
найти точку D, скорость которой направлена вдоль АВ, опустим перпендикуляр EмсцD нз точки Eмсц на эту прямую. Величина скорости υD=ωEмсцD, где ω — угловая скорость звена АВ, определить которую можно по известной скорости шарнира А:
Подставляя это значение ω в предыдущее равенство, найдем
но из прямоугольного треугольника ADEмсц имеем
Чтобы определить угловую скорость коромысла O2B, найдем модуль скорости точки В, принадлежащей шатуну:
Угловую скорость ω2 коромысла определим по скорости υВ, так как точка В принадлежит и коромыслу:
Применяя теорему синусов, получим ответ.
Ответ.
Задача №5
Найти мгновенный центр скоростей звена BD (рис. 143, а) для случая, когда: 1) φ1 = 45 o ; 2) φ12 = 90 o ; 3) φ1=0 o .
Решение. В этом плоском механизме звено BD продето в качающуюся шайбу C и, двигаясь в плоскости чертежа, постоянно проходит через неподвижную точку С. Следовательно, скорость той точки звена BD, которая в данное мгновение совпадает с точкой С, направлена вдоль звена BD. Точка В (палец кривошипа) описывает окружность с центром в точке А, и ее скорость всегда перпендикулярна к АВ.
1. Рассмотрим первое заданное положение механизма и нанесем на чертеж (рис. 143, б) скорости точки В и точки звена BD, совпадающей при данном положении механизма с точкой С. Восставляя перпендикуляры к скоростям в точках В и С, найдем в точке их пересечения мгновенный центр скоростей звена В.
2. При φ12 = 90 o (рис. 143, в) перпендикуляры, восставленные в точках В и C к направлениям скоростей, становятся параллельными между собой и мгновенный центр скоростей уходит в бесконечность. При даином положении механизма распределение скоростей точек звена BD не соответствует такому, какое бывает при вращательном движении, угловая скорость звена равна нулю, линейные скорости всех точек звена одинаковы.
3. Третье заданное положение механизма изображено на рис. 143, г. Как и в предыдущих случаях, восставляем перпендикуляры к скоростям точки В и к прямой ВС. Перпендикуляры пересекаются в точке С, следовательно, при данном положении механизма мгновенный центр скоростей звена BD находится в точке С. Скорость той точки звена, которая совпадает с точкой С, в данное мгновение равна нулю. Рассматриваемое положение звена называется «крайним положением» (или «мертвым положением»), Картина распределения скоростей точек звена BD в данном положении такова, как будто оно вращается вокруг точки С.
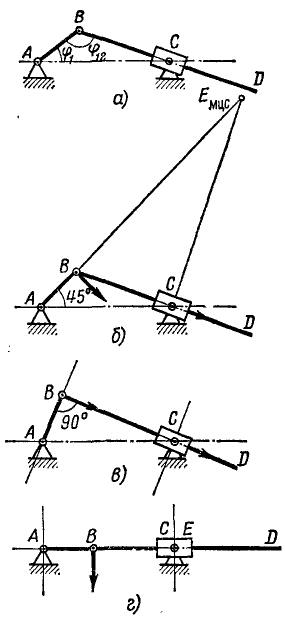
Рис. 143
Ответ. 1) на пересечении линии AB и перпендикуляра, восставленного в точке C к линии ВС; 2) в бесконечности в направлении АВ; 3) в точке С.
Задача №6
Прямая движется в плоскости. Показать, что величина скорости той точки прямой, которая ближе всех отстоит от мгновенного центра скоростей, равна проекции скорости любой другой точки прямой на эту же прямую (рис. 144).
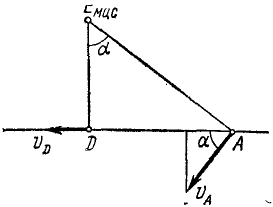
Рис. 144
Решение. Дано: прямая, мгновенный центр скоростей Eмцс и угловая скорость ω этой прямой. Опустив из точки Eмцс перпендикуляр на данную прямую, определим точку D (см. рис. 144) прямой, находящуюся на кратчайшем расстоянии от мгновенного центра скоростей. Скорость точки D равна υD=ω . Eмцс D и направлена перпендикулярно к EмцсD, т. е. по данной прямой.
Возьмем на той же прямой какую-либо другую точку А. Скорость точки А перпендикулярна к АЕмцс и равна
Как видно из чертежа,
Так как точку А мы выбрали на прямой совершенно произвольно, то, следовательно, полученное равенство справедливо для всякой точки прямой.
Ответ. Проекции скоростей всех точек прямой на эту прямую равны между собой.
Задача №7
Линейка эллипсографа AB (см. рис. 89 на стр. 139) совершает карданово движение, причем ползун А линейки движется по оси Оу, а ползун В—по оси Ох. При каком положении линейки скорость ползуна А вдвое больше скорости ползуна В?
Решение. Эту задачу, уже решенную нами ранее (см. № 43 на стр. 139, № 57 на стр. 160), можно просто решить, пользуясь мгновенным центром скоростей. Восставим перпендикуляры в точках A и В к направлениям их скоростей. Перпендикуляры пересекутся в точке Eмсц — мгновенном центре скоростей линейки (эти построения на рис. 88 не сделаны). Величины скоростей точек линейки пропорциональны расстоянию этих точек от точки Емцс. Чтобы выполнялось условие υА=2uB, точка А должна отстоять от точки Eмсц вдвое дальше, чем точка В, а так как OAEмсцB является прямоугольником, то хB = 2уA.
Ответ. хB = 2уA
При качении плоской фигуры по неподвижной кривой, лежащей в плоскости фигуры, мгновенный центр скоростей находится в точке касания
IV. При решении задач бывает полезно иметь в виду, что если какая-либо плоская фигура катится по другой плоской фигуре, лежащей с ней в одной плоскости (например, подвижная шестеренка катится по неподвижной), то скорость точки катящейся фигуры, находящейся в данное мгновение в соприкосновении с неподвижной фигурой, должна быть равна нулю, если, конечно, качение не сопровождается проскальзыванием или пробуксовыванием. А так как в каждое мгновение на фигуре, совершающей плоское движение, имеется только одна точка со скоростью, равной нулю (мгновенный центр скоростей), то, следовательно, он и находится в точке касания.
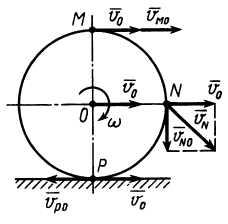
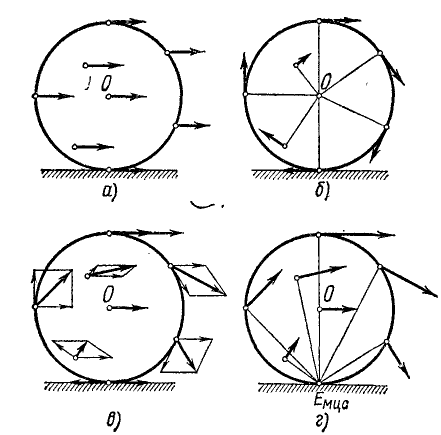
Пусть, например, колесо катится по прямолинейному рельсу (рис. 145). Рассмотрим движение колеса как составное, состоящее из переносного поступательного движения вместе с осью колеса О и относительного вращательного движения вокруг этой оси. На рис. 145, а изображены переносные скорости некоторых точек колеса, а на рис. 145, б—вращательные скорости тех же точек относительно центра колеса. В случае качения без скольжения и без буксования вращательная скорость точек, лежащих на ободе колеса, по модулю равна скорости оси, так как при повороте колеса на один полный оборот его ось переместится на 2πr, а точки обода опишут в их относительном вращательном движении окружности той же длины. Абсолютные скорости точек колеса изображены на рис. 145, в. Эти абсолютные скорости можно получить как вращательные скорости вокруг мгновенного центра скоростей, совпадающего с точкой касания колеса и рельса (рис. 145,г).
Мгновенный центр скоростей лежит на самой катящейся фигуре или на неизменно с ней связанной подвижной плоскости. Точку, совпадающую с мгновенным центром скоростей, но лежащую на неподвижной плоскости, по которой движется фигура, называют мгновенным центром вращений. В рассмотренном примере мгновенный центр скоростей лежит на ободе колеса, а мгновенный центр вращений—на рельсе.
Задача №8
Зацепление, приводящее в быстрое вращение точильный камень, устроено следующим образом (рис. 146, а): стержень IV посредством особой ручки приводится во вращение вокруг оси O1 с угловой скоростью ω4. На конце O2 стержня находится палец, на который свободно надето колесо II радиуса r2. При вращении ручки палец заставляет колесо II катиться без скольжения по наружному неподвижному кругу III радиуса r3. При этом благодаря трению колесо II вращает без скольжения колесо I радиуса r1, свободно насаженное на ось O1 и неизменно связанное с осью точила. По данному радиусу r3 наружной неподвижной обоймы найти такое значение rl, чтобы выполнялось соотношение 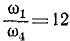
Решение. В этом плоском механизме колесо II катится без скольжения по неподвижному колесу III и мгновенный центр скоростей колеса II находится в точке их касания (рис. 146, б). Палец O2 принадлежит стержню IV, и его скорость
Та же точка O2 принадлежит колесу II, что позволяет определить его угловую скорость:
Теперь нетрудно определить скорость точки В касания колес I и II. Эта точка отстоит от мгновенного центра скоростей на расстоянии 2r2, т. е. в два раза дальше, чем точка O2, поэтому и скорость ее вдвое больше:
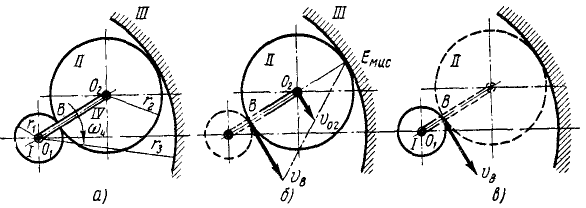
Рис. 146
Та же точка В принадлежит колесу I (рис. 146, в) и для определения угловой скорости этого колеса надо поделить окружную скорость на его радиус:
откуда
Это отношение должно равняться 12, т. е.
Но нам задан радиус rs неподвижного обода III. Как видно из чертежа (см. рис. 146, a) r3 = r1 + 2r2.
Решая совместно два последних соотношения, получим ответ.
Ответ.
Задача №9
Доказать теорему: если скорости υА и υB двух точек А и В плоской фигуры перпендикулярны к прямой АВ, соединяющей эти точки, то мгновенный центр скоростей делит отрезок А В на части, пропорциональные величинам скоростей внешним образом, когда скорости направлены в одну сторону, или внутренним образом, когда скорости направлены в противоположные стороны.
Доказательство. Движение фигуры плоское. Мгновенный центр скоростей должен лежать на прямой АВ, так как скорости перпендикулярны к прямым, соединяющим их точки приложения с мгновенным центром скоростей (рис. 147, а). Вращение фигуры может происходить в данное мгновение лишь в одну сторону (на нашем рисунке—по часовой стрелке), поэтому’ мгновенный центр скоростей должен лежать по одну сторону от точек А и В, если их скорости направлены одинаково, и между ними, если скорости противоположны (рис. 147, б). В обоих случаях скорости точек пропорциональны их расстояниям от мгновенного центра скоростей:
что и требовалось доказать.
Ответ.
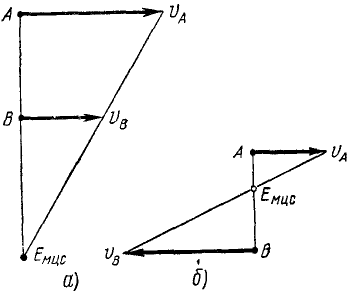
Рис. 147
При плоском движении фигуры подвижная центроида катится без скольжения по неподвижной
Центроиды**. В различные моменты времени мгновенный центр скоростей находится в различных точках. Геометрическое место мгновенных центров скоростей, т. е. совокупность всех точек, в которых за время движения находился мцс, называют центроидой. Покажем, что центроида является непрерывной линией и мцс всегда перемешается из точки, в которой он в данное мгновение находится, в какую-нибудь соседнюю, смежную точку.
Пусть в мгновение t мцс находился где-либо в точке А, а через промежуток времени Δt переместился в точку B. В мгновение t1=t + ∆t точка А уже не является мгновенным центром скоростей и имеет скорость υA = ω∙AB, направленную перпендикулярно к АВ. Если промежуток времени Δt мал, то скорость, приобретенная точкой А к моменту t+Δt, тоже должна быть мала, потому что скорости точек фигуры не могут изменяться скачками. При ∆t, стремящемся к нулю, скорость υ точки А тоже стремится к нулю, а так как угловая скорость ω фигуры нулю не равна, то, следовательно, к нулю стремится АВ, т. е. мгновенный центр скоростей во время движения фигуры перемещается непрерывно. Если мы отметим все точки фигуры, которые были или будут мгновенными центрами скоростей, то получим некоторую непрерывную кривую.
Положения мгновенных центров скоростей можно отметить и на подвижной плоскости х’Еу’, неизменно связанной с фигурой, и на неподвижной плоскости хОу. Геометрическое место мгновенных центров скоростей на подвижной плоскости называют подвижной центроидой. Геометрическое место мгновенных центров скоростей на неподвижной плоскости (мгновенных центров вращений) называют неподвижной центроидой. В рассмотренном выше примере качения колеса по рельсу подвижной центроидой является обод колеса, а неподвижной центроидой—рельс.
Покажем, что при всяком плоском движении подвижная ueπτpo∙ ида катится без скольжения по неподвижной.
Предположим, что кроме точек фигуры имеется одна геометрическая точка, назовем ее следящей точкой, которая не принадлежит этой плоской фигуре и движется относительно нее, совпадая в каждое мгновение с мгновенным центром скоростей. Скорость следящей точки в ее движении по центроиде называют сменной скоростью мгновенного центра скоростей. Следовательно, подсменной скоростью мгновенного центра скоростей понимают ту скорость, с которой передается от мгновенного центра скоростей смежной по центроиде точке основное его свойство—иметь в данное мгновение скорость, равную нулю.
Во время движения фигуры следящая точка перемещается и относительно неподвижных координат и в самой движущейся фигуре. Ее движение относительно неподвижных координат хОу есть абсолютное движение по неподвижной центроиде. Ее движение по движущейся фигуре есть относительное движение, движение по подвижной центроиде. Пусть (рис. 148, а) кривая ЕЕ изображает неподвижную центроиду, а кривая E1E1—подвижную. Предположим, что обе центроиды в мгновенном центре скоростей пересекаются.
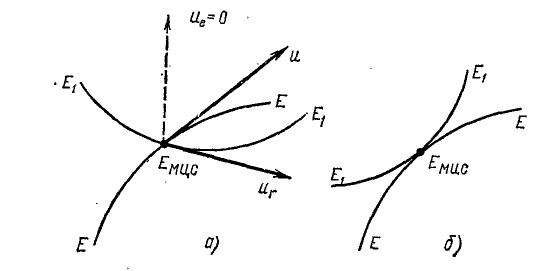
Рис. 148
В таком случае вектор абсолютной сменной скорости 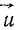
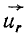
Переносной скоростью называют абсолютную скорость той точки среды (в данном случае фигуры), с которой в данное мгновение совпадает движущаяся точка. В данном случае переносная скорость следящей точки есть скорость мгновенного центра скоростей. Следовательно
Мы доказали, что сменная скорость следящей точки по неподвижной центроиде геометрически равна ее сменной скорости по подвижной центроиде. Это означает, что обе центроиды в мгновенном центре скоростей имеют общую касательную, т. е. не пересекаются, а лишь соприкасаются в этой точке. Наше предположение о пересечении центроид оказалось неправильным и рис. 148, а должен быть заменен рисунком 148, б. Из равенства абсолютной и относительной сменных скоростей следует, что за одни и те же промежутки времени следящая точка передвигается по подвижной и неподвижной центроидам на одинаковые расстояния, т. е., что при движении плоской фигуры подвижная центроида катится по неподвижной без скольжения.
Задача №10
Эллипсограф (рис. 149) состоит из линейки AB длиной l, ползуны А и В которой скользят в пазах крестовины. При движении линейки точки ее описывают эллипсы. Указать другой механизм, в котором отрезок AB=l совершает точно такое же движение.
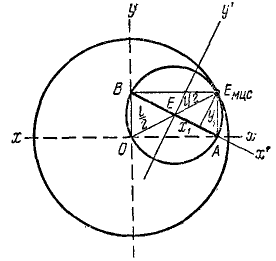
Рис. 149
Решение. Движение линейки AB плоское, а следовательно, оно может быть осуществлено качением подвижной центроиды по неподвижной. Примем прорези крестовины за оси основной системы координат хОу. Подвижную систему координат х’Еу’ свяжем с линейкой, взяв за начало ее середину Е. Мгновенный центр скоростей находится на пересечении перпендикуляров, восставленных к скоростям точек А и В (см. задачу № 89), и, как видно из чертежа, находится на расстоянии OEмцс= Z от точки О и на расстоянии 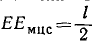
радиуса 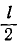
радиуса I с центром в О.
Если мы сделаем две зубчатые шестерни с внутренним зацеплением радиусов l и 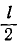
Ответ. Круги Лагира.
Скорости точек плоской фигуры можно определить графически планом скоростей
План скоростей. На рисунке 150, а изображена фигура, находящаяся в плоском движении и скорости υА и υВ двух ее произвольных точек А и В. Напомним, что проекции скоростей этих точек на прямую AB равны между собой. От какой-либо точки О, не принадлежащей этой фигуре (рис. 150, б), отложим направленные отрезки 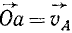
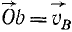
Построим план скоростей (рис. 150, г), приняв произвольную точку О за полюс плана скоростей, т. е. за центр плоского пучка абсолютных скоростей точек фигуры. Отложим от полюса луч Oa, равный в некотором масштабе скорости 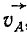
Пусть скорость точки К фигуры не известна ни по величине, ни по направлению. Соединим точку К с точками A и B фигуры, скорости которых известны (см. рис. 150, в). На плане скоростей (см. рис. 150, г) проведем от точки а линию, перпендикулярную направлению AK на фигуре. По только что доказанному, конец направленного отрезка Ok, изображающего скорость точки К, должен лежать на этом перпендикуляре.
Проведем от точки b плана скоростей прямую, перпендикулярную направлению BK на фигуре, и повторим наши рассуждения: конец направленного отрезка Ok должен лежать и на этом перпендикуляре.
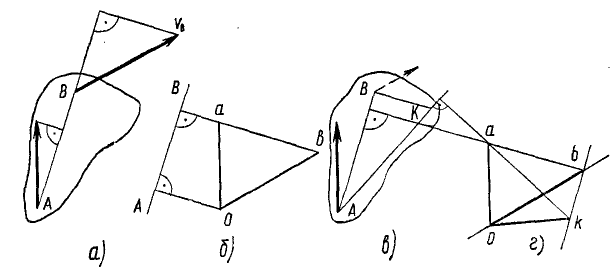
Рис. 150
Следовательно, точка k плана скоростей лежит на пересечении перпендикуляров, восставленных из точек а и b к направлениям AK и BK, а отрезок Ok плана скоростей изображает скорость точки К фигуры.
Отсюда можно вывести следующий графический метод определения скоростей точек фигуры при плоском движении (см. рис. 150, в, г).
Если известна скорость одной точки А фигуры и направление скорости другой точки В, то для определения скорости всякой точки К фигуры надо:
- 1) от произвольной точки О (полюса плана скоростей) отложить направленный отрезок Oa, изображающий скорости точки А;
- 2) через полюс О провести направление, параллельное направлению скорости точки В;
- 3) от точки а плана скоростей провести прямую, перпендикулярную отрезку АВ, соединяющему точки Л и В фигуры, до пересечения в точке b с указанным в п. 2 направлением. Отрезок Ob изобразит скорость точки В;
- 4) от точки а плана скоростей провести направление, перпендикулярное отрезку AK на фигуре, а от точки b плана скоростей провести направление, перпендикулярное отрезку BK на фигуре до их пересечения в точке k. Отрезок Ok изобразит скорость точки К;
- 5) многоугольник abk . плана скоростей подобен многоугольнику A, B, K . фигуры и повернут относительно него на 90°, так как стороны их взаимно перпендикулярны.
Поскольку отрезки Oa, Ob, Ok, . соединяющие полюс 0 с вершинами a, b, k, . плана скоростей, изображают абсолютные скорости точек А, В, К, • • •, очевидно, что отрезки ab, ak, bk, . изображают в том же масштабе относительные скорости этих точек.
Таким образом, план скоростей плоской фигуры представляет собой плоский пучок, лучи которого изображают абсолютные скорости точек плоской фигуры, а отрезки, соединяющие концы лучей,—относительные скорости соответствующих точек. План скоростей можно построить не только для неизменяемой фигуры, но и для целого механизма, как это показано при решении задачи № 93.
Задача №11
Определить скорости точек А, В и D механизма, изображенного на рис. 151, а, в положении φ = 30 o и при следующих данных: ω = 20 сек -1 , OA = 50 мм, OC=200 мм, АВ=250 мv, BD = 200 мм.
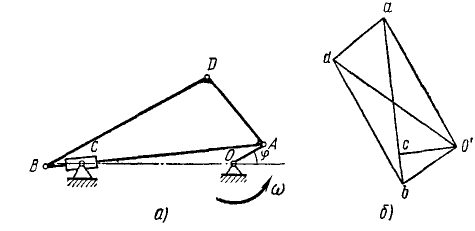
Рис. 151
Решение. Прежде чем строить план скоростей, нужно точно в масштабе построить план механизма при заданном положении. От точки О’ (рис. 151, б) откладываем перпендикулярно к OA в масштабе отрезок O’a=υА-= 20 . 50=1000 мм/сек. На нашем рисунке принят масштаб: 1000 мм/сек = 25 мм. Скорость точки звена АВ, совпадающей при данном положении механизма с точкой С, направлена по АВ. Поэтому от полюса О’ отложим параллельно AB на правление этой скорости, а от точки а проведем перпендикуляр к этому направлению. В пересечении получим точку с. Отрезок acb плана скоростей подобен отрезку ACB механизма. Точку b плана находим по подобию, сохраняя те же пропорции.
Проводим от точки а направление перпендикулярно к AD, а от точки b — направление перпендикулярно к BD и в пересечении находим точку d.
Полученная на плане фигура acbd подобна фигуре ACBD механизма. Скорости точек механизма по величине и направлению изображаются отрезками, соединяющими полюс плана О’ с соответствующими точками плана скоростей.
Ответ. υА =1000 мм/сек, yВ = 450 мм/ сек, уD= 1040 мм/сек.
Задача №12
Скорость топки А фигуры, движущейся в своей плоскости, изображена в заданном масштабе вектором υА (рис. 152, а). Указано направление скорости точки В. Определить графически скорости точек В и С.
Решение. Задачу решим тремя способами. Все эти три способа графические и результат зависит от точности выполнения чертежей.
1-й способ (по основной теореме кинематики твердого тела). Проведем прямую AB через точки А и В (рис. 152, б) и спроецируем на нее вектор скорости υА. От точки В по этой прямой отложим отрезок, равный проекции на нее υА и от конца этого отрезка восставим перпендикуляр до пересечения с направлением скорости точки В. Вектор скорости точки В определен.
Проведем прямую через точку А и С. Спроецируем на нее υA, отложим от точки C отрезок, равный этой проекции, и от конца его восставим перпендикуляр к АС. Проведем прямую через точки В и С, спроецируем на нее υB, отложим от точки C отрезок, равный этой проекции и от его конца восставим перпендикуляр к ВС. Проводим вектор υC от точки C до пересечения перпендикуляров.
2-й способ (по плану скоростей) . От произвольной точки О отложим направленный отрезок Oa-υА (рис. 152, в). От той же точки О проведем прямую, параллельную вектору скорости точки В До пересечения с этой прямой в какой-то точке b проведем от точки а отрезок ab перпендикулярно АВ. Вектор скорости точки В представлен отрезком Ob.
От точки а проведем прямую, перпендикулярную АВ, а от точки b, перпендикулярную ВС. Эти прямые пересекутся в какой-то точке с. Отрезок Oc по величине и направлению представляет скорость точки С.
3-й способ (по мгновенному центру скоростей). От точек A и В восставим перпендикуляры к направлениям скоростей до нх пересечения в мгновенном центре скоростей Eмцс . Соединим Eмцс с концом а вектора υА. Тангенс угла δ между отрезками Emuc Л и Eмцс а, соединяющими Emuc с началом Лис концом а вектора скорости какой-либо точки A фигуры, равен в принятом масштабе угловой скорости фигуры:
Проведя отрезок Eмцс b под углом δ к отрезку Eмцс В до Пересечения с заданным направлением вектора скорости υB, определим скорость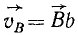
Для определения скорости всякой точки C фигуры надо провести отрезок Eмцс C и под углом δ к нему отрезок Eмцс с до пересечения в точке с с перпендикуляром, восставленным в точке C к отрезку Eмцс C. Вектор скорости 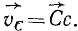
Ускорение любой точки фигуры, совершающей плоское движение, равно геометрической сумме ускорения полюса и ускорений точки при вращении фигуры относительно полюса
Ускорение точек фигуры при плоском движении*. Чтобы определить ускорение точки К плоской фигуры, надо продифференцировать равенства (114), выражающие скорость этой точки. Введем обозначения: х1 = х—хЕ и y1 = y—уF и перепишем эти равенства в следующем виде:
По формулам Эйлера (см. 89)
Подставляя, находим
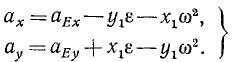
В правых частях этих равенств согласно (95) вторые члены выражают проекции касательного, а третьи —проекции центростремительного ускорения точки К во вращательном движении фигуры относительно полюса Е. Они отличаются от известных нам равенств (95) только тем, что в данном случае ось вращения проходит не через начало координат О, а через полюс E (рис. 153).
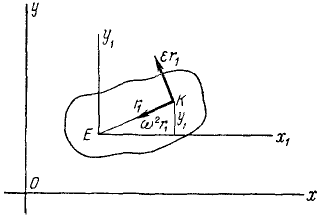
Рис. 153
Эти равенства показывают, что проекции на какую-либо неподвижную ось ускорения каждой точки К фигуры равны алгебраической сумме проекций на эту ось трех его составляющих: ускорения полюса Е, касательного ускорения точки К во вращении фигуры вокруг полюса E и центростремительного ускорения точки К в том же движении фигуры.
Если вместо алгебраической суммы проекций мы пожелаем взять геометрическую сумму ускорений, то вектор ускорения точки K мы определим как сумму трех векторов: ускорения полюса Е, касательного ускорения точки К во вращательном движении фигуры вокруг полюса и центростремительного ускорения точки K в том же движении фигуры, т. е.
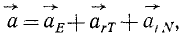
где, обозначив через r1 расстояние данной точки от полюса Е, имеем
Задача №13
Электропоезд при отходе со станции движется по прямолинейному участку пути с ускорением 3 м/сек 2 , причем колеса катятся без буксования и без скольжения. Найти ускорение мгновенного центра скоростей колеса через 2 сек после отхода поезда, если радиус колеса 0,5 м.
Решение. Мгновенный центр скоростей лежит на ободе колеса в точке касания его с рельсом. Движение колеса рассмотрим как составное, состоящее из переносного (поступательного и прямолинейного) движения вместе с центром E колеса и относительного вращательного вокруг оси колеса (рис. 154).
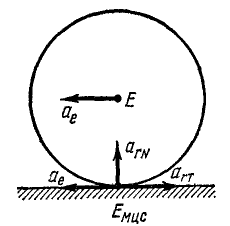
Рис. 154
Скорость поезда, а следовательно, и скорость точки E через 2 сек при равноускоренном движении равна υ-a-rt = 6 м/сек.
Деля эту величину на расстояние точки E от мгновенного центра скоростей Eмцс, находим угловую скорость колеса в конце второй секунды:
Определим также угловое ускорение колеса:
Теперь мы располагаем всеми данными для определения ускорения точек колеса по формуле (104»). Ускорение мгновенного центра скоростей, как и всякой точки колеса, выражено суммой трех составляющих: 1) переносного ускорения ае, равного ускорению полюса Е, но приложенного в данной точке Eмцс (величина ускорения задана 3 м/сек 2 ; если поезд движется влево, то и ускорение направлено горизонтально влево, см. рис. 154); 2) касательного ускорения точки при вращении колеса вокруг центра Е; эта составляющая равна εr = 6 . 0,5 =3 м/сек 2 . Если поезд движется влево, то колеcа вращаются против вращения часовой стрелки и эта составляющая ускорения в нижней точке колеса направлена вправо по касательной; 3) центростремительного ускорения, равного ω 2 r= 144 . 0,5 = 72 м/сек 2 и направленного к центру колеса.
Направления этих двух составляющих у всех точек обода колеса различны. В наинизшей точке абсолютное ускорение найдем, складывая три его составляющие. Оно равно 72 м/сек 2 и направлено вверх. Абсолютная скорость мгновенного центра скоростей в данное мгновение равна нулю, абсолютное ускорение мгновенного центра скоростей нулю не равно.
Ответ. а = 72 м/сек 2 и направлено вверх.
Обратим внимание на то, что точка фигуры (в данном случае колеса), в которой находится мгновенный центр скоростей, не имеет скорости (υмцс =0), но имеет ускорение (αмцс≠0). Через весьма малый промежуток времени Δt эта же точка фигуры будет иметь некоторую скорость Δυ = αмцсΔt, перпендикулярную к прямой, соединяющей ее с новым положением мгновенного центра скоростей, т. е. перпендикулярную к общей касательной к центроидам. То же направление всегда имеет и αмцс.
Ту точку фигуры, совершающей плоское движение, ускорение которой в данное мгновение равно нулю, называют мгновенным центром ускорений плоской фигуры
Мгновенный центр ускорений при плоском движении
Итак, ускорения точек фигуры складываются из переносного ускорения в поступательном движении вместе с полюсом E и из относительного ускорения во вращательном движении вокруг полюса Е. В поступательном движении ускорения всех точек фигуры одинаковы и равны ускорению полюса Е. Во вращательном движении ускорения всех точек фигуры различны между собой. Если фигура в данное мгновение имеет угловую скорость ω и угловое ускорение ε, то ускорение какой-либо точки K, принадлежащей этой фигуре, по модулю равно:
и составляет с отрезком ЕK угол μ, тангенс которого
Таким образом, различные точки К фигуры имеют при вращении фигуры различные по величине и по направлению ускорения. На всей фигуре нет двух точек с одинаковыми векторами ускорений.
Вместе с тем на самой фигуре или на плоскости, вращающейся вместе с нею, во всякое мгновение есть одна точка, имеющая любой, наперед заданный нами, вектор ускорения ar. В частности, всегда можно найти на плоскости фигуры такую точку, у которой в данное мгновение вектор ускорения в относительном вращательном движении равен и противоположен вектору ускорения в переносном поступательном движении, а следовательно, абсолютное ускорение этой точки равно нулю. Ее называют мгновенным центром ускорений плоской фигуры. Мы будем приписывать ей индекс мцу.
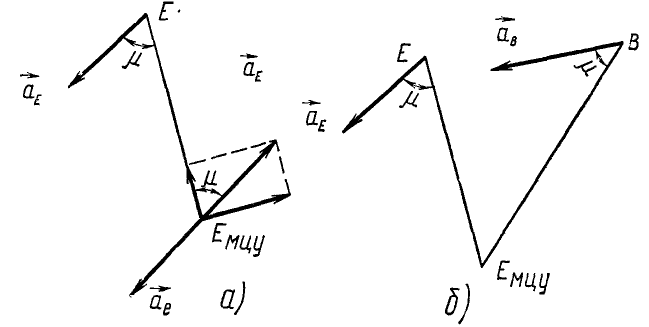
Рис. 155
Чтобы определить положение мгновенного центра усорений Емцу на плоскости фигуры, отложим (рис. 155, а) от полюса E (за полюс может быть принята любая точка фигуры) отрезок EEмцу определенной длины:
Пусть этот отрезок составляет с ускорением 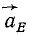
Угол μ лежит в пределах между —90° и +90 o . Конечно, если ε > 0, то угол μ надо отмерять в положительном направлении, т. е. против хода часовой стрелки, если же ε / )
Следовательно, картина распределения ускорений на время dt такова, как будто бы фигура вращается в своей плоскости вокруг Емцу с угловой скоростью ω и с угловым ускорением ε. Это не относится к их нормальным и касательным составляющим, как показано в задаче № 97.
В виду того, что угол μ между абсолютным ускорением точки фигуры и отрезком, соединяющим эту точку с Емцу, для всех точек фигуры один и тот же, надо сделать заключение, что Емцу находится на пересечении прямых, проведенных под углом 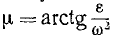
Задача №14
Определить координаты мгновенного центра ускорений плоской фигуры, если известны ее угловая скорость, угловое ускорение, а также координаты хЕ и уЕ и проекции ускорений аЕх и аЕу одной из точек E этой фигуры.
Решение. Проекции ускорений каждой точки К связаны с координатами xl = x—хЕ и у1=у — уЕ. этой точки соотношениями 119 (см стр. 235). Ускорение мгновенного центра ускорений равно нулю, поэтому, заменяя в 119 х и у на хмцу и Умиу и подставляя нули вместо ах и ау, получим:
Умножая первое из этих равенств на ω 2 , а второе на —ε и складывая, найдем хмцу, а умножая первое равенство на +ε, а второе на ω 2 и складывая, найдем ординату.
Задача №15
В планетарном механизме шестеренка радиуса R =100 мм (рис. 156, а) катится против хода часовой стрелки по неподвижной шестеренке радиуса R1 = 480 мм , имея в данное мгновение угловую скорость ω = 2ceκ -1 и угловое ускорение ε= 1,655 ceκ -2 . Найти построением мгновенный центр ускорений, его координаты (по формулам, выведенным в задаче № 96), найти полное, нормальное и касательное ускорения центра шестеренки О, мгновенного центра скоростей Eмцс и диаметрально противоположной точки А. Определить абсолютное нормальное и абсолютное касательное ускорения точки А.
Решение. Мгновенный центр скоростей находится в точке Eмцс касания шестерен. Окружность подвижной шестерни является подвижной центроидой, а окружность неподвижной шестерни —неподвижной центроидой Построим оси координат с началом в Eмцс, направив ось абсцисс влево, т. е. в ту сторону, куда передвигается точка касания центроид при качении подвижной центроиды по неподвижной. Ось ординат направим вниз (правая система).
Скорость центра О подвижной шестеренки определим по угловой скорости фигуры и по расстоянию точки О от мгновенного центра скоростей
Определим касательное ускорение точки О:
Точка О описывает окружность радиуса R+ R1= 100 + 480 = 580 мм и вектор касательного ускорения направлен по касательной к окружности, описываемой точкой О. Величину нормального ускорения определим, поделив квадрат скорости точки О на радиус описываемой ею окружности
направлен вектор нормального ускорения к центру окружности, описываемой точкой О.
Вектор полного абсолютного ускорения точки О направлен по диагонали прямоугольника, построенного на этих составляющих и по модулю равен:
Зная ω, ε и ускорение точки О, мы могли бы найти мгновенный центр ускорений и, пользуясь им, определить ускорения остальных точек. Однако целесообразно сначала по схеме (110′), приняв точку О за полюс, найти ускорение мгновенного центра скоростей. Заполнив эту схему, получим (рис. 156, б).
Полное абсолютное ускорение точки Eмцс равно геометрической сумме составляющих. Относительное касательное ускорение равно по величине и противоположно по направлению переносному касательному, их сумма равна нулю. Относительное нормальное направлено по одной прямой, но в противоположную сторону с переносным нормальным ускорением. Следовательно абсолютное ускорение точки Eмцс по величине равно
и направлено к точке О, т. е. по оси ординат в отрицательную сторону. Следовательно:
Точка подвижной шестеренки, которая в данное мгновение является центром скоростей, описывает эпициклоиду и в заданное мгновение находится в точке возврата своей траектории. Таким образом абсолютное ускорение мгновенного центра скоростей является абсолютным касательным ускорением. Нормальное ускорение мгновенного центра скоростей равно нулю.
Найдем теперь мгновенный центр ускорений. Определим сначала угол μ:
По таблицам определяем
Повернув вектор ускорения амцу на этот угол против хода часовой стрелки (потому что в > 0), отложим в найденном направлении отрезок (рис. 156, а)
Конец Eмцу этого отрезка является мгновенным центром ускорений подвижной шестеренки в данное мгновение. Координаты этой точки в выбранной нами системе отсчета можно определить непосредственно по чертежу или же подсчитать по общим формулам, полученным при решении предыдущей задачи № 96,
Теперь для определения ускорения точки А надо знать только ее расстояние от Eмцу. Это расстояние легко определить по формуле аналитической геометрии или по теореме косинуса:
Извлекая корень, находим
Остается лишь подсчитать по формулам относительное нормальное ускорение
и отложить его от точки А по направлению к Eмцу, затем подсчитать относительное касательное ускорение
и отложить его перпендикулярно к Eмцу, сообразуясь со знаком. Полное относительное ускорение можно определить как диагональ прямоугольника или непосредственно подсчитать по формуле
и отложить вектор под углом μ (в нашей задаче +22 o 30 , ) к отрезку AEмцу.
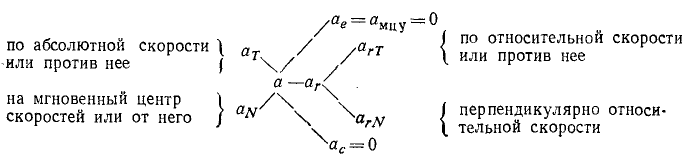
Движение плоской фигуры мы рассматривали как составное, состоящее из переносного поступательного вместе с полюсом и относительного вращательного вокруг полюса, приняв за полюс мгновенный центр ускорений. При таком условии переносное ускорение и ускорение Кориолиса равны нулю и в схеме (110′) остается только одна ее часть. Полное относительное ускорение становится тождественным полному абсолютному ускорению. Но чтобы получить абсолютное нормальное ускорение и абсолютное касательное ускорение точки, мы должны спроецировать это полное ускорение точки на прямую, соединяющую эту точку с мгновенным центром скоростей (а не ускорений), и на прямую, ей перпендикулярную, т. е. надо спроецировать ускорение на главную нормаль к абсолютной траектории точки и на направление абсолютной скорости. Схема (ПО’) принимает вид:
Чтобы вычислить эти проекции, найдем сначала по теореме синусов угол между направлениями на Eмцс и Eмцy ν=12 o 45′ и затем
Приняв Eмцy за полюс, мы достигли того, что абсолютное ускорение всякой точки фигуры стало равно ее относительному ycκopeнию. Но мы должны помнить, что нормальная и касательная составляющие абсолютного ускорения не равны нормальной и касательной составляющим относительного ускорения. Это происходит оттого, что не тождественны между собой абсолютное и относительное движения точек. Так, например, в рассмотренной задаче № 97 точка О в абсолютном движении описывает окружность радиусом R + R1 = 580 мм с центром в точке O1, а в относительном движении движется вокруг Eмцy по дуге радиуса ОEмцy, точка А в абсолютном движении описывает гипоциклоиду, а в относительном движется по дуге окружности радиуса 132,5 мм с центром Eмцy.
Понятия о мгновенном центре скоростей и мгновенном центре ускорений плоской фигуры очень удобны для вычислений, но связанные с ними картины распределения скоростей и ускорений не отображают полностью реальное движение фигуры. Это происходит потому, что вводя эти понятия мы рассматривали движение лишь в данное мгновение, при данном положении тела, т. е. пытались рассматривать движение как бы в отрыве от основных условий его существования— времени и пространства. Результаты такого подхода к вопросу, конечно, не могут быть полными и объективными.
План ускорений
Решение задач на тему: ускорение.
Задача №16
Фигура движется в своей плоскости. Известно положение мгновенного центра ускорений Eмцy и вектор ускорения одной точки А фигуры. Найти построением ускорение точки В той же фигуры. На рис. 157 заданы отрезок АВ, точка Eмцy и вектор aA.
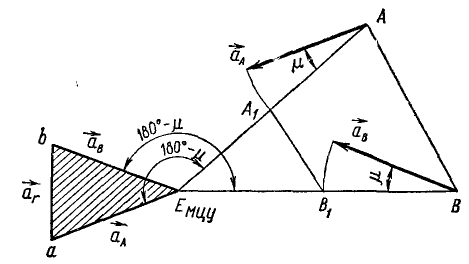
Рис. 157
Решение. Проведя прямую АEмцy, мы получим угол μ, который составляет ускорения всех точек фигуры с прямыми, соединяющими эти точки с Eмцy. Под таким же углом μ должен быть наклонен искомый вектор aВ к отрезку ВEмцy. Для определения модуля этого вектора сделаем следующее построение. Повернем вектор aA на угол μ до его совпадения с отрезком AEмцy, когда конец повернутого вектора будет в точке A1. Из точки А, параллельно AB проведем прямую A1B1 до пересечения в точке B1 с BEмцy. Из подобия треугольников ABEмцy и A1В1Емцy заключаем, что отрезок BB1 представляет модуль ускорения точки В аВ = BEмцy 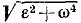
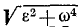
Примечание. Метод, примененный при решении этой задачи, является общим в кинематике плоского движения и им можно определить ускорение любой точки фигуры, если известно положение Емцу. Вариант этого метода, называемый методом плана ускорений, позволяет определить ускорения точек фигуры и при неизвестном положении Емцу, лишь бы были известны ускорения двух точек фигуры, или ускорение одной точки, направление ускорения другой точки и план скоростей фигуры. Построим план ускорений для отрезка АВ. Для этого отложим от Емцу направленные отрезки
Соединив точки а и b, мы получим треугольник ABEмцу заштрихованный на чертеже и подобный треугольнику ABEмцу. Действительно оба треугольника имеют по равному углу (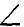
Заметим, что наше построение не нарушится, если при построении заштрихованного треугольника мы возьмем вершину не в Eмцу, а в любой точке е неподвижной плоскости. Точку е называют полюсом плана ускорений. Применение плана ускорений к определению ускорений точек фигуры показано в задаче № 99.
Задача №17
Фигура (рис. 158) движется в своей плоскости. По заданным ускорениям точек А и В определить ускорения точек D и С.
Решение. От произвольной точки е вне фигуры откладываем направленные отрезки 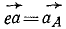
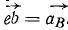
Понятие об общем случае движения твердого тела
Движение свободного тела состоит из поступательного и сферического движений
Уравнение движения свободного тела
В самом общем случае движение твердого тела мы представим как составное, разложив его на переносное поступательное вместе с какой-либо точкой Е, принятой нами за полюс, и относительное сферическое вокруг полюса.
Движение свободного твердого тела может быть описано шестью
Рис. 159
уравнениями: тремя уравнениями (78) поступательного движения и тремя уравнениями (96) сферического движения:
xE=x(t), yE=y(t), zE=z (t), ψ = ψ (t), φ = φ(t), 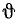
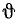
Во всякое мгновение мы представляем движение тела как поступательное с некоторой скоростью 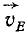
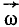
Поступательное движение тела со скоростью υE в свою очередь разложим на два поступательных движения, одно из которых происходит со скоростью υE1, направленной по мгновенной оси вращения, а другое —со скоростью υE2, направленной перпендикулярно ω.
Эту скорость υE2 поступательного движения мы представим как пару угловых скоростей (рис. 159, б), момент которой равен υE2, а плечо 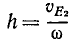
Следовательно, картина распределения скоростей твердого тела в самом общем случае такова, как будто тело вращается в данное мгновение вокруг некоторой оси и одновременно скользит вдоль нее. Эту ось называют мгновенной осью вращения—скольжения, или мгновенной винтовой осью.
Таким образом, картина распределения скоростей в твердом теле вполне аналогична динамическому винту (см. § 15), выражающему общий случай приведения системы сил, приложенной к твердому телу.
Движение свободного тела мы разложили. на поступательное движение, определяемое движением произвольной точки Е, принятой за полюс, и сферическое движение вокруг полюса E и представили уравнениями движения (122).
Очевидно, что и скорость любой точки К этого тела мы получим как скорость точки в составном движении по параллелограмму скоростей, как сумму скорости полюса и относительной скорости точки при сферическом движении тела вокруг полюса.
Аналогично и ускорение любой точки свободного твердого тела равно геометрической сумме ускорения полюса и ускорения этой точки при сферическом движении тела..
| Рекомендую подробно изучить предмет: |
|
| Ещё лекции с примерами решения и объяснением: |
- Мгновенный центр скоростей
- Мгновенный центр ускорений
- Мгновенный центр вращения
- Вращение твердого тела вокруг неподвижной точки
- Трение
- Пространственная система сил
- Центр тяжести
- Кинематика точки
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
📽️ Видео
Урок 101. Скатывание тела с наклонной плоскостиСкачать

Движение колеса без проскальзывания, качение | Олимпиадная физика, кинематика | 9 – 11 классСкачать

Вращательное движение. 10 класс.Скачать

Траектория и уравнения движения точки. Задача 1Скачать

Мгновенный центр вращенияСкачать

Наклонная плоскостьСкачать

Урок 93. Основное уравнение динамики вращательного движенияСкачать

ДВИЖЕНИЕ ПО НАКЛОННОЙ ПЛОСКОСТИ | механика 10 классСкачать

Качение колеса без проскальзывания. Лекция 2-3Скачать

колесо катится с ускорениемСкачать

Как работает колесоСкачать

Момент инерцииСкачать

Тема: Сила уравнений движения и основная задача механикиСкачать

Урок 94. Вычисление моментов инерции телСкачать

Урок 87. Движение по наклонной плоскости (ч.1)Скачать

Скорости точек плоской фигурыСкачать

Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать