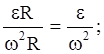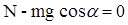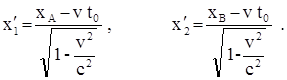Уравнение движения имеет вид x at bt3 найти среднюю скорость движения

Готовое решение: Заказ №8335

Тип работы: Задача

Статус: Выполнен (Зачтена преподавателем ВУЗа)

Предмет: Физика

Дата выполнения: 07.08.2020

Цена: 227 руб.

Чтобы получить решение , напишите мне в WhatsApp , оплатите, и я Вам вышлю файлы.

Кстати, если эта работа не по вашей теме или не по вашим данным , не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу , я смогу выполнить её в срок 1-3 дня!

Описание и исходные данные задания, 50% решения + фотография:

№5-1 1. Уравнение прямолинейного движения материальной точки x = At + Bt3, где A = 2,5 м/с, B = 0,05 м/с3. Определить средние значения скорости и ускорения за первые 3 с движения и сравнить их с мгновенными значениями этих величин в начальный и конечный моменты этого отрезка времени.

Поскольку и , то координата точки растёт с течением времени. То есть точка движется в одну сторону. Тогда средняя скорость точки в интервале времени от до будет равна: . Найдём среднюю скорость точки в заданном интервале времени: м/с. Найдём закон изменения мгновенной скорости точки: .

• Материальная точка движется прямолинейно. Уравнение движения имеет вид: x = At + Bt3, где A = 3 м/с, B = 0,06 м/с3. Найти скорость v и ускорение точки в моменты времени t1 = 0 и t2 = 3 с. Найти средние значения скорости и ускорения за первые 3 с движения. Условие 2 107. Материальная точка движется прямолинейно. Уравнение движения имеет вид x = At + Bt3, где A = 3 м/с, B = 0,06 м/с3. Найдите скорость v и ускорение a точки в момент времени t1 = 0 и t2 = 3 с. Каковы средние значения скорости и ускорения за первые 3 с движения? Условие 3 1.04. Материальная точка движется прямолинейно. Уравнение движения имеет вид x = At + Bt3, где A = 3 м/с, B = 0,06 м/с3. Найти скорость v и ускорение точки в моменты времени t1 = 0 и t2 = 3 с. Каковы средние значения скорости и ускорения за первые 3 с движения?
• Точка движется по прямой согласно уравнению x = At + Bt3, где A = 6 м/с, B = 0,06 м/с3. Определите среднюю скорость точки в интервале времени от t1 = 2 с до t2 = 6 с.
• Точка движется по прямой согласно уравнению x = At + Bt3, где A = 6 м/с, B = 0,125 м/с3. Определить среднюю скорость точки в интервале времени от t1 = 2 с до t2 = 6 с и среднее ускорение.
• Прямолинейное движение материальной точки описывается уравнением x = At + Bt3, где A = 2,0 м/с, B = 0,04 м/с3. Определить величину средней скорости и среднего ускорения за первые 4 с движения.

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Видео:Найти среднюю скоростьСкачать

Примеры решения задач. Задача 1 Уравнение движения точки по прямой имеет вид: x = A+Bt+Ct3, где А = 4 м, В = 2 м/c, С = 0,2 м/с3

Задача 1 Уравнение движения точки по прямой имеет вид: x = A+Bt+Ct 3 , где А = 4 м, В = 2 м/c, С = 0,2 м/с 3 . Найти: 1) положение точки в моменты времени t = 2 c и t = 5 с; 2) среднюю скорость за время, протекшее между этими моментами; 3) мгновенные скорости в указан­ные моменты времени; 4) среднее ускорение за указанный промежуток вре­мени; 5) мгно­венные ускорения в указанные моменты времени.

x = A + Bt + Ct 3 A = 4 м B = 2 м/c C = 0,2 м/c 3 t1 = 2 c; t2 = 5 c	Решение 1. Чтобы найти координаты точки, надо в уравнение дви­же­­­ния подставить значения t1 и t2: x1 = (4+2×2+0,2×2 3 ) м = 9,6 м, x2 = (4+2×5+0,2×5 3 ) м = 39 м.
x1, x2, — ? u1, u2 — ? , a1, a2 — ?	2. Средняя скорость ,

м/с = 9,8 м/с.

3. Мгновенные скорости найдем, продифференцировав по времени уравнение движения:

u₁ = (2+3×0,2×2 2 ) м/с = 4,4 м/c;

u₂ = (2+3×0,2×5 2 ) м/с = 17 м/с.

4. Среднее ускорение ,

м/c 2 = 4,2 м/с 2 .

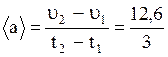
5. Мгновенное ускорение получим, если продифференцируем по времени выражение для скорости: a = 2×3×Ct = 6Ct.

a₁ = 6×0,2×2 м/c 2 = 2,4 м/с 2 ;

a₂ = 6×0,2×5 м/с 2 = 6 м/с 2 .

Ответ: x₁ = 9,6 м; x₂ = 39 м; áuñ = 9,8 м/с; u₁ = 4,4 м/c; u₂ = 17 м/с; áаñ = 4,2 м/с 2 ; a₁ = 2,4 м/с 2 ; a₂ = 6 м/с 2 .

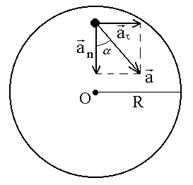
Задача 2 Маховик вращается равноускоренно. Найти угол a, ко­то­рый составляет вектор полного ускорения любой точки маховика с радиусом в тот момент, когда маховик совершит первые N=2 оборота.

w0 = 0 N = 2 e = const	Решение Разложив вектор точки М на тангенци­аль­ное и нормальное уско­ре­ния, видим, что иско­мый угол определяется соотно­шением tga=at/an.
a — ?

Поскольку в условии дано лишь число оборотов, перейдем к угловым величинам. Применив формулы: a_t = eR, a_n = w 2 R, где R – радиус маховика, получим

tga =

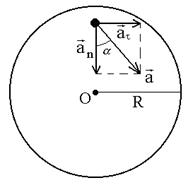
так как маховик вращается равноускоренно, найдем связь между величинами e и w;

Поскольку w₀ = 0; j = 2pN, то w 2 = 2e×2pN = 4pNe.

Подставим это значение в формулу, получим:

a » 2,3°.

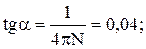
Задача 3 Две гири с массами m₁ = 2 кг и m₂ = 1 кг соединены нитью, пе­ре­ки­ну­той через невесомый блок. Найти ускорение a, с которым движутся гири, и силу натяжения нити . Трением в блоке пренебречь.

m1 = 2 кг m2 = 1 кг	Решение Воспользуемся для решения задачи основным законом динамики где – равнодействующая всех сил, действующих на тело.
a, FН — ?

На тело 1 и тело 2 действуют только две силы – сила тяжести и сила

натяжения нити. Для первого тела имеем

(1)

для второго тела

. (2)

Так как сила трения в блоке отсутствует,

.

Ускорения тел а₁ и а₂ направлены в противоположные стороны и равны по модулю:

.

Получаем из выражений (1) и (2) систему уравнений

Выберем ось Х, как показано на рисунке и запишем полученную систему уравнений

в проекции на ось Х

Решая эту систему относительно а и F_Н, получаем:

= 3,3 м/с 2 ; = 13 Н.

Ответ: a= 3,3 м/c 2 ; F_H = 13 Н.

Задача 4 К ободу однородного диска радиусом R=0,2 м прило­жена каса­тель­ная сила F=98,1 Н. При вращении на диск действует момент сил трения

М_ТР=4,9 Н×м. Найти массу m диска, если известно, что диск вращается с угловым ускорением e=100 рад/с 2 .

R = 0,2 м F = 98,1 Н MТР = 4,9 Н×м e = 100 рад / c 2	Решение Воспользуемся основным законом динамики вращательного движения, записанным для оси вращения, направление которой совпадает с направлением угловой скорости: , где — момент сил, приложенных к телу,
m — ?

относительно выбранной оси ( M_F — момент силы F, M_тр – момент сил трения);

— момент инерции диска.

Учитывая, что M_F=F×R, получаем .

Отсюда ; m = 7,4 кг.

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.007 сек.)

Видео:Физика - перемещение, скорость и ускорение. Графики движения.Скачать

Движение материальной точки задано уравнением x=At+Bt², где A =4 м/с, В=-0,05 м/с². Определить момент времени, в который скорость v точки

Видео:Уравнение движения тела дано в виде x=2−3t. ВычислиСкачать

Ваш ответ

Видео:Средняя скорость движения, урожайность. 6 класс.Скачать

решение вопроса

Видео:Уравнение движенияСкачать

Похожие вопросы

• Все категории
• экономические 43,429
• гуманитарные 33,634
• юридические 17,906
• школьный раздел 608,227
• разное 16,858

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Уравнение движения. Как найти время и место встречи двух тел ???Скачать

Примеры решения задач по теме №1

«Механика и элементы специальной теории относительности»

Задача 1 Уравнение движения точки по прямой имеет вид: x = A+Bt+Ct 3 , где А = 4 м, В = 2 м/c, С = 0,2 м/с 3 . Найти: 1) положение точки в моменты времени t = 2 c и t = 5 с; 2) среднюю скорость за время, протекшее между этими моментами; 3) мгновенные скорости в указан­ные моменты времени; 4) среднее ускорение за указанный промежуток вре­мени; 5) мгно­венные ускорения в указанные моменты времени.

x = A + Bt + Ct 3 A = 4 м B = 2 м/c C = 0,2 м/c 3 t1 = 2 c; t2 = 5 c	Решение 1. Чтобы найти координаты точки, надо в уравнение дви­же­­­ния подставить значения t1 и t2: x1 = (4+2×2+0,2×2 3 ) м = 9,6 м, x2 = (4+2×5+0,2×5 3 ) м = 39 м.
x1, x2, — ? u1, u2 — ? , a1, a2 — ?	2. Средняя скорость ,

м/с = 9,8 м/с.

3. Мгновенные скорости найдем, продифференцировав по времени уравнение движения:

u₁ = (2+3×0,2×2 2 ) м/с = 4,4 м/c;

u₂ = (2+3×0,2×5 2 ) м/с = 17 м/с.

4. Среднее ускорение ,

м/c 2 = 4,2 м/с 2 .

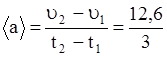
5. Мгновенное ускорение получим, если продифференцируем по времени выражение для скорости: a = 2×3×Ct = 6Ct.

a₁ = 6×0,2×2 м/c 2 = 2,4 м/с 2 ;

a₂ = 6×0,2×5 м/с 2 = 6 м/с 2 .

Ответ: x₁ = 9,6 м; x₂ = 39 м; áuñ = 9,8 м/с; u₁ = 4,4 м/c; u₂ = 17 м/с; áаñ = 4,2 м/с 2 ; a₁ = 2,4 м/с 2 ; a₂ = 6 м/с 2 .

Задача 2 Маховик вращается равноускоренно. Найти угол a, ко­то­рый составляет вектор полного ускорения любой точки маховика с радиусом в тот момент, когда маховик совершит первые N=2 оборота.

w0 = 0 N = 2 e = const	Решение Разложив вектор точки М на тангенци­аль­ное и нормальное уско­ре­ния, видим, что иско­мый угол определяется соотно­шением tga=at/an.
a — ?

Поскольку в условии дано лишь число оборотов, перейдем к угловым величинам. Применив формулы: a_t = eR, a_n = w 2 R, где R – радиус маховика, получим

tga =

так как маховик вращается равноускоренно, найдем связь между величинами e и w;

Поскольку w₀ = 0; j = 2pN, то w 2 = 2e×2pN = 4pNe.

Подставим это значение в формулу, получим:

a » 2,3°.

Задача 3 Две гири с массами m₁ = 2 кг и m₂ = 1 кг соединены нитью, пе­ре­ки­ну­той через невесомый блок. Найти ускорение a, с которым движутся гири, и силу натяжения нити . Трением в блоке пренебречь.

m1 = 2 кг m2 = 1 кг	Решение Воспользуемся для решения задачи основным законом динамики где – равнодействующая всех сил, действующих на тело.
a, FН — ?

На тело 1 и тело 2 действуют только две силы – сила тяжести и сила

натяжения нити. Для первого тела имеем

(1)

для второго тела

. (2)

Так как сила трения в блоке отсутствует,

.

Ускорения тел а₁ и а₂ направлены в противоположные стороны и равны по модулю:

.

Получаем из выражений (1) и (2) систему уравнений

Выберем ось Х, как показано на рисунке и запишем полученную систему уравнений

в проекции на ось Х

Решая эту систему относительно а и F_Н, получаем:

= 3,3 м/с 2 ; = 13 Н.

Ответ: a= 3,3 м/c 2 ; F_H = 13 Н.

Задача 4 К ободу однородного диска радиусом R=0,2 м прило­жена каса­тель­ная сила F=98,1 Н. При вращении на диск действует момент сил трения

М_ТР=4,9 Н×м. Найти массу m диска, если известно, что диск вращается с угловым ускорением e=100 рад/с 2 .

R = 0,2 м F = 98,1 Н MТР = 4,9 Н×м e = 100 рад / c 2	Решение Воспользуемся основным законом динамики вращательного движения, записанным для оси вращения, направление которой совпадает с направлением угловой скорости: , где — момент сил, приложенных к телу,
m — ?

относительно выбранной оси ( M_F — момент силы F, M_тр – момент сил трения);

— момент инерции диска.

Учитывая, что M_F=F×R, получаем .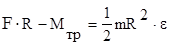

Отсюда ; m = 7,4 кг.

Задача 5 На гладкой горизонтальной поверхности находятся две одинаковые соприкасающиеся шайбы. Третья такая же шайба налетает на них со скоростью v₀ = 6 м/с, направленной по общей касательной к неподвижным шайбам. После столкновения налетевшая шайба движется вдоль первоначального направления со скоростью v₁ = 2 м/с. Найти величину энергии, перешедшей во внутреннюю энергию тел при столкновении. Масса каждой шайбы m = 100 г.

Решение

Рассмотрим систему, состоящую из трех шайб. Данная система не является консервативной, так как в условии задачи требуется найти энергию, перешедшую во внутреннюю энергию тел при их взаимодействии. Значит, удар не является абсолютно упругим, и механическая энергия системы не сохраняется. Строго говоря, эта система не является и замкнутой, так как на тела действуют внешние силы тяжести и реакции поверхности, на которой находятся шайбы. Однако эти внешние силы направлены вертикально и их проекции на любую горизонтально проведенную ось равны нулю. Поэтому при описании удара тел можно пользоваться законом сохранения импульса (для его проекций на любую горизонтальную ось).

Рассмотрим два состояния выбранной системы тел: 1) налетающая шайба движется со скоростью v₀ вдоль горизонтальной оси X, остальные две шайбы покоятся; 2) после частично неупругого удара налетающая шайба движется вдоль оси X с меньшей скоростью v₁, а две первоначально покоившиеся шайбы разлетаются со скоростями v₂ и v₃.

Поскольку размеры всех шайб одинаковы, то скорости v₂ и v₃, направленные вдоль прямых,

соединяющих центры шайб в момент удара, составляют одинаковые углы a = 30 о с осью X, а так как массы всех шайб по условию равны, то очевидно, что скорости v₂ и v₃ равны по модулю, то есть v₂ = v₃ = v.

Теперь запишем закон сохранения импульса для проекций импульсов взаимодействующих тел на ось X:

Тогда mv₀ = mv₁ + 2 mv сosa.

Отсюда .

Энергию, перешедшую во внутреннюю энергию тел при частично неупругом ударе, можно найти как разность кинетической энергии налетающей шайбы до удара и суммарной кинетической энергии всех тел после удара:

.

Ответ: DU = 1,07 Дж.

Задача 6 Небольшое тело массой m равномерно втащили на горку, действуя силой, которая в каждой точке направлена по касательной к траектории. Найти работу этой силы, если высота горки h, длина ее основания l, и коэффициент трения m.

Решение

Работу, совершаемую силой , можно найти по общему определению работы:

.

Для этого необходимо предварительно найти силу . Рассмотрим перемещаемое тело в произвольной точке траектории его движения. На тело действуют четыре силы: сила тяжести , сила реакции опоры , сила трения скольжения и внешняя сила . Поскольку по условию задачи тело движется равномерно, то векторная сумма этих сил равна нулю:

Выберем координатные оси х и у таким образом, чтобы ось х была направлена по каса­тельной к траектории (вдоль перемещения ).

Запишем векторное равенство в проекциях на эти координатные оси:

oсь x:

oсь y:

Тогда 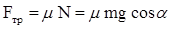, а модуль силы

.

Теперь можно найти выражение для элементарной работы, совершаемой силой F при перемещении тела на расстояние dr. При этом учтем, что угол между векторами и равен нулю и косинус этого угла равен единице.

Тогда .

Из рис. видно, что , где dh — элементарное приращение высоты при перемещении тела на расстояние dr, а , то есть элементарному перемещению тела в горизонтальном направлении.

Тогда ,

и полная работа, совершаемая силой F при втаскивании тела на горку:

.

Ответ: .

Задача 7 Круглая платформа радиусом R=1,0 м, момент инерции которой J=130 кг×м 2 , вращается по инерции вокруг вертикальной оси, делая n₁=1,0 об/с. На краю платформы стоит человек, масса которого m=70 кг. Сколько оборотов в секунду n₂ будет совершать платформа, если человек перейдет в её центр? Момент инерции человека рассчитывать как для материальной точки.

где L₁ — импульс системы «платформа + человек на краю платформы», L₂ — импульс системы «платформа + человек в центре платформы».

где mR 2 — момент инерции человека, J₁ = J+mR 2 — момент инерции системы «платформа + человек на краю платформы», J₂ — момент инерции системы «платформа + человек в центре платформы», w₁ и w₂ — соответствующие угловые скорости системы. Решая систему уравнений (1) — (3), получаем

Задача 8 В условно неподвижной системе отсчета К в точках с коорди­натами x_A и x_B = x_A + l, где l = 1 км, одновременно происходят два события A и B. На каком расстоянии l¢_АВ друг от друга зафиксирует эти события наблюдатель в системе К¢, движущейся со скоростью v = 0,4×с вдоль оси X? Какой промежуток времени Dt¢ между этими событиями зафиксирует наблюдатель в системе К¢?

Решение

Обозначим через t₀ момент времени, когда в системе К происходят события А и В. Тогда событие А в этой системе обладает пространственно – временными координатами x_A и t₀, а событие В – координатами x_B и t₀. В системе К¢ событие А обладает пространственно–временными координатами x₁¢ и t₁¢, а событие В – координатами x₂¢ и t₂¢. Связь координат каждого из событий можно записать с помощью преобразований Лоренца.

Найдя разность этих выражений, получим расстояние между точками, в которых происходят события А и В в системе К¢.

Видно, что расстояние l¢_АВ, разделяющее события А и В в любой системе, движущейся относительно К, больше, чем это же расстояние, измеренное в системе К, в которой оба события одновременны. Рассчитаем расстояние l¢_АВ.

Моменты времени, в которые в системе К¢ наблюдатель зафиксирует события А и В, также могут быть найдены из преобразований Лоренца:

Видно, что события А и В в системе отсчета К¢ не являются одновремен­ными. Если x_B > x_A и система К¢ движется в положительном направлении оси X, как и задано в условии, то t₂¢ — t₁¢ .

📽️ Видео

Задачи на движение. Учимся решать задачи на движение. Способы решения задач на движение.Скачать

Как найти среднюю скорость движения автомобиля?Скачать

Задача на среднюю скоростьСкачать

УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать

Физика - уравнения равноускоренного движенияСкачать

Урок 16 (осн) Средняя скорость. Вычисление пути и времени движенияСкачать

Уравнение равномерного прямолинейного движения | Физика 10 класс #3 | ИнфоурокСкачать

Траектория и уравнения движения точки. Задача 1Скачать

Задачи на движение 3. Средняя скоростьСкачать

Решение графических задач на равномерное движениеСкачать

Уравнение движения с постоянным ускорением | Физика 10 класс #6 | ИнфоурокСкачать

Урок 12. Равномерное прямолинейное движениеСкачать

РАВНОМЕРНОЕ ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ | скорость движения | УРАВНЕНИЕ ДВИЖЕНИЯСкачать

7 класс урок №10 Расчет скорости и средней скоростиСкачать